| 七自由度机器人运动学分析 |
从目前所掌握的资料来看,国外相关企业已有采用铲除冶炼浇铸金属液表面渣滓皮层的工业机器人,但效果不尽理想,而且相关资料比较少。
在我国,冶炼厂中的浮渣铲除都是由人工在高温、多粉尘、空气质量差等环境下完成,这样不仅影响工人的身体健康,而且工作效率低下。因此,设计出一种既能代替人劳动,又能提高工作效率的机器人,对于冶炼行业是十分有意义的。
1 浮渣铲除机器人的机构设计浮渣铲除机器人的设计是仿造人工铲除过程的手臂运动方式,它的运动是由底座的直线运动,腰部(立柱)回转运动,大臂的仰俯运动,小臂的仰俯运动、腕部的回转、仰俯、左右摆动这七个自由度组成(参照图 1)。
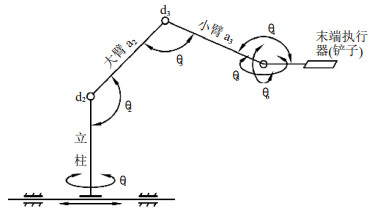 |
| 图 1 浮渣铲除机器人结构简图 |
2 运动学参数
浮渣铲除机器人为串联杆式机械手,其动态特性具有高度非线性,因此用适当的数学方程式(数学模型)表示其运动是十分重要的,而应用这些数学模型来预测和控制其运动过程,因此运动学分析也是控制的基础。
以Denavit-Hartenberg(D-H)表示方法描述机器人坐标系统如图 2,相邻杆件间位置和姿态可用4×4的齐次变换矩阵(称为A矩阵,也叫关节变换矩阵)描述,即:
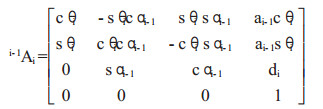
|
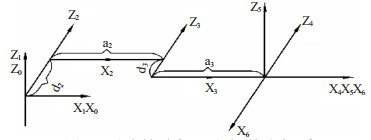 |
| 图 2 浮渣铲除机器人杆件坐标系 |
则由D-H矩阵经过变换【2】得到相邻连杆变换通式i-1Ti为:

|
(1) |
其中:ai-1、αi-1、di和θi是坐标系i-1和i之间的位置参数。
将各个连杆变换i-1Ti(i=1, 2, …n,为关节号数)顺序相乘,得到末端执行器的坐标系{n}相对于基坐标系{0}的总的矩阵变换通式:0Tn= 0T11T2…n-1Tn。
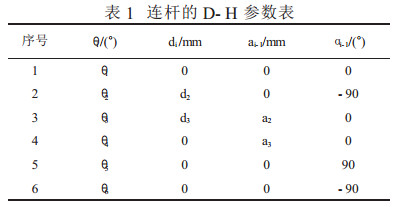
图 2和图 1比较起来会发现有所不同,其一,底座的直线运动可以单独来控制,因此在运动学分析时属于冗余自由度,不予考虑,只分析其他6个自由度。其二,腰部回转关节的原点并不在实际位置,但在实际的计算过程中,无论关节是高一点还是低一点,机器人的运动并不会有任何差异。因此坐标系原点选择在大臂和立柱的交点处。连杆的D-H参数列于表 1中。
| 表 1 连杆的D-H参数表 |
 |
| 点击放大 |
将各个连杆变换i-1Ti(i=1, 2, …n)顺序相乘,得到末端执行器的坐标系{n}相对于基坐标系{0}的总的矩阵变换通式为:

|
(2) |
根据式(1)、(2)得到浮渣铲除机器人的末端执行器(铲子)的变化矩阵0T6,0T6即为关节变量θ1,θ2,…θ6的函数。在求解运动方程过程中,其简写形式如下:
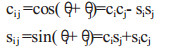
|
(3) |
式中:ci、cj为cosθi和cosθj的缩写,si、sj为sinθi和sinθj的缩写。
从(3)式可算出各个连杆的变换矩阵:

|
(4) |

|
(5) |

|
(6) |

|
(7) |
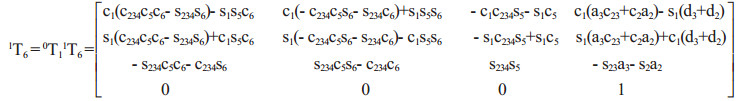
|
(8) |
由

|
可得出:

|
由上述0T6的矩阵,描述了机器人末端连杆坐标系相对基坐标系的位置。
4 结语(1)研究机器人机构运动学的目的就是要建立机器人各运动构件与末端执行器在空间的位置、姿态之间的关系,建立机器人手臂运动的数学模型,为控制机器人的运动提供分析的方法和手段,为仿真研究手臂的运动特性和设计控制器实现预定的功能提供一种高效、方便的方法。
(2)可以把人从恶劣的工作环境中解脱出来,既解决了劳动力保护问题,又为提高生产效率创造了条件,具有显著的经济效益和社会效益。
| [1] |
Saeed B Niku. 机器人学导论——分析、系统及应用[M]. 孙富春, 朱纪洪, 刘国栋, 等, 译, 孙增圻, 审校. 北京: 电子工业出版社, 2004.
|
| [2] |
蔡自兴.
机器人学[M]. 北京: 清华大学出版社, 2000.
|
| [3] |
余达太, 马香峰, 郗安民, 等.
工业机器人应用工程[M]. 北京: 冶金工业出版社, 1999.
|
| [4] |
Zhang Kai, Hu Dejin, Liu Chengliang. Study on Singular Configurations and Computer Simulation of 6R Robt[J].
Chinese Journal of Mechanical Engineeiring, 2004(2): 177–180. |
| [5] |
SYu J, Quick G, Paulicks W, et al. Transputer-based Robot Control System for Six -joint Robot Manipulators[J].
Robotics and Computer-Integrated Manufacturing, 1998(4): 111–119. |
 2007, Vol. 21
2007, Vol. 21
