| 漂塘矿区一井定向工作实践 |
漂塘矿区328~616中段全部为地面平硐开拓方式,三维控制全部由地面三角网控制,由平硐引入各中段,有Ⅰ级和Ⅱ级导线控制,导线点同时引入水准高程。
268中段为漂塘矿区深部开采中段, 副井于2001年完成提升设施安装。由于主井尚未到达施工位置,所以此中段平面控制投影只能先实施一井定向的方式由上部中段传递至深部中段,以保证深部中段的开拓工程能按设计施工。因268中段担负着漂塘矿区未来的工程接替,平面控制精度要求较高,所以选择控制精度较高的联系三角形法[1]。三角形布置为延伸形三角形,即二个锐角与一个大钝角,上、下两近井测站尽可能在垂线的延长线上,使角度解算的误差不受量边误差影响。
为使人员联络方便,选择了没有信号房的上部448中段作为井上投点平面,并对448中段近井导线进行了井下Ⅰ级导线规范检测,从而精密确定了起始边方位角。笔者只讲述井上传递成果与精度分析,因保证了井上投点精度即相对保证了268中段起始边的方位精度要求。
1 一井定向的点位选择与观测 1.1 点位选择在竖井能铅垂通过的两个点位上, 由上中段悬挂两直径0.5mm钢丝至深部中段, 用15kg以上垂球悬挂, 两钢丝尽量间距最大, 同时在上、下中段埋高近
井点,与两钢丝组成近似直线的上、下两个三角形,即γ角与α角,γ′角与α′角趋近于零,MC与C1D尽量大于20m。A钢、B钢分别为铅垂钢丝,C为上井近井点,C1为下井近井点,实线为上部中段传递图形,虚线为深部中段传递图形,即一井定向中的联系三角形法,见图 1
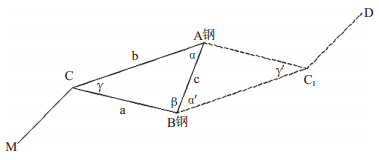 |
| 图 1 上下中段传递图 |
此乃根据正弦公式推算出解算角中误差公式分析得出。当α≈0(小于2)、β≈180(°大于178)时,tgα≈0,tg β≈0,cos γ≈1,cos α≈1,cos β≈-1。解算角中误差公式可变为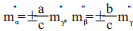
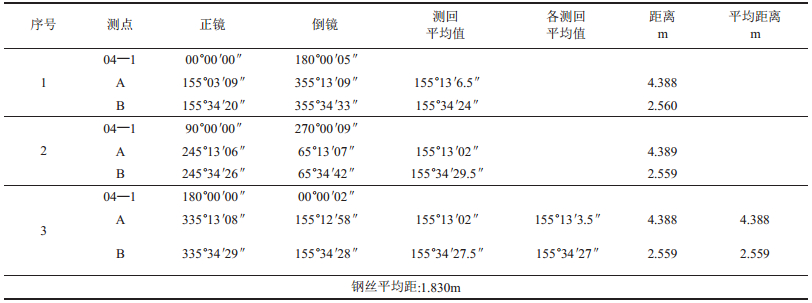
上部中段对井下与近井口点进行井下Ⅰ级导线规范检测, 从而精度确定起始边的方位角, 即M-C边的方位角。笔者只讲述了井上三角形传递成果与精度分析,因保证了井上投点精度即相对保证了井下起始边的方位精度要求。此次观测使用仪器为国产“苏J2”光学经纬仪,距离丈量为50m钢尺。在近井C点设站施测了3个测回,符合规范最低要求测回数。观测结果见表 1。
| 表 1 观测结果表 |
 |
| 点击放大 |
2 一井定向的精度分析 2.1 内业计算
由前观测成果可得出γ=0°21′23.5″, 小于2°。因a=2.599m,b=4.388m, c=1.830m, 则AB边的解算值为:

|
α角计算值:
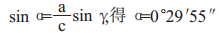
|
β角计算值:

|
ABC三角形内角和解算值:
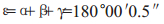
|
(1) γ角的观测值分析及α、β角的测角中误差[2 ]。从观测成果表中可知γ角三测回最大差CA方向为4.5″, CB方向为5.5″, 而两边最大差之和10″, 仍小于规范2e(即2×6″)12″, 说明此角的观测精度达到要求。
解算角α中误差:
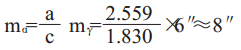
|
解算角β中误差:
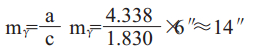
|
式中:mγ为6″,由使用级别经纬仪所决定。
从解算角中误差可知α角符合2(e即12″)规范精度要求,角中误差略大于12″,说明此角精度略为欠缺。但传递方向是由C-A-B-C′-D伸展的,全部延锐角传递,使β角的影响降到最小。
(2) 联系三角形ABC内角和观测值与解算值之和与理论值180°之差0.5″, 远小于规范要求20″, 说明各观测值与联系三角形各要素正确无误, 且精度足够传递计算, 可不作内角和平差。
(3) AB钢丝距离丈量与解算值的比较。丈量值-解算值=0.0009m, 大大小于联系定向测量规范要求之差0.002m。根据公式c计2 =a2+b2-2ab cos γ,可知γ角的观测精度符合要求。
3 结语通过此工作实践,以及在后来的本中段与上中段风井准确贯穿可看出,此次定向精度能满足下部中段的平面控制,因贯穿风井与定向井导线长度为580余m,至中段开采边界只剩200m,完全能满足此中段各项工程的施工放样。也体会到只要在施测过程中做到按规范操作,增强工作责任心,不出粗差,在无先进测绘仪器的情况下,也能保证传递中段的平面控制精度。
| [1] |
孔祥元, 梅是义.
控制测量学[M]. 修订版. 武汉: 武汉大学出版社, 2002.
|
| [2] |
张正禄.
工程测量学[M]. 修订版. 武汉: 武汉大学出版社, 2002.
|
 2007, Vol. 21
2007, Vol. 21
