| 岩体边坡开挖卸荷稳定性分析 |
在土木、水利水电、矿山工程中,都不可避免地存在岩土边坡稳定性问题。影响岩体边坡稳定性的因素很多,如岩土性质、岩体结构、水、风化程度、地震、地应力以及人为因素等等。岩体中的节理、裂隙等弱面结构的构造及分布形式,岩体的受力及变形状态等是影响岩体边坡稳定的重要因素,其中由于边坡开挖引起的卸荷对岩体边坡的作用机理与加载作用破坏机理不同。笔者结合黄麦岭露天边坡的工程实际,讨论裂隙及卸荷对边坡稳定性的影响。
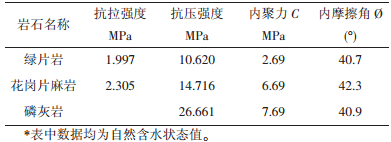
1 边坡岩性及应力变形分布规律黄麦岭露天采场为岩质边坡,设计最终边坡角为44º,台阶坡面角为70º。边坡岩体的物理力学性质见表 1。边坡剖面典型的主应力分布如图 1所示。从图 1中可知:①愈邻近坡面,最大主应力方向愈接近于与坡面平行。其它各处应力随深度增加其方向趋于垂直向下,大小递增;②软弱岩体(或层面)的分布使得应力的分布发生变化,邻近软弱岩体(或层面)的应力大小变化较为明显;③在自重的条件下计入地应力作用时,坡底及坡的下半部分主压应力值增加较为明显。当边坡开挖后,边坡附近的应力会发生很大变化,包括主应力的大小和方向,主应力差等,这就使得边坡表面原有微裂纹扩展并产生新的裂纹.在宏观上表现为边坡向自由面的膨胀现象。
| 表 1 边坡岩体的物理力学性质 |
 |
| 点击放大 |
 |
| 图 1 边坡应力分布图 |
该边坡在开挖前,一直处于稳定状态,开挖后,随着开采水平的下移(台阶高度为l0m),边坡出现规模不等的浅层和深层滑坡。现场堪察表明,主要是由于原生节理裂隙、开挖卸荷、爆破振动等因素而引起的。根据现场监测及分析,边坡位移的基本规律有以下几个方面。
(1) 水平向位移比垂直向位移小一个数量级,前者处于毫米或厘米级,后者处于厘米或分米量级,位移总体指向朝下。
(2) 坡面附近点的位移方向受原始应力场的影响,当竖向应力与水平应力比值较大时,水平向位移向于边坡的倾斜方向。
(3) 当仅考虑自重或既有自重又计入近静水压力状的原始地应力(σx=-3.17 σy=-2.96 MPa)时,弹性的线性分析与弹塑性的非线性分析结果相同,表明与此相对应的外力条件下坡面附近未进入塑性变形状态。
(4) 增加原始地应力值(压应力),边坡各处的压缩位移量相应增大。
(5) 不提高地应力分量的最大值,但改变地应力分量间的比值,位移量发生相应的变化,当此比值较大时,易出现塑性变形。
下面从理论上就这几个方面的影响机理进行分析。
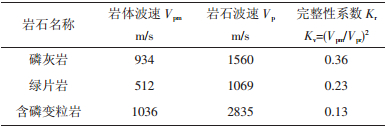
2 裂隙的分形特性及起裂失稳所研究的岩质边坡中,节理裂隙比较发育,其完整性系数仅为0.11~0.36, 见表 2。滑体扩展范围主要受节理裂隙面控制。
| 表 2 边坡岩体完整性系数 |
 |
| 点击放大 |
裂隙的结构由两部分组成:一部分是裂隙面的起伏程度; 另一部分是裂隙面的张开度。裂隙面的起伏符合分形特征,并且不同粗糙度的裂隙具有不同的分形维数[1]。根据裂隙表面形态分形维数和张开度分形维数生成的裂隙结构模型见图 2[2]。
 |
| 图 2 分形裂隙模拟 |
岩体中存在的大量弱面和微裂纹,在加载前,这些弱面和颗粒界面上就存在大量的原始微裂纹,在荷载作用下这些原始微裂纹大多发生界面延伸,即沿原方向扩展。当其扩展到弱面、颗粒与基质的交界面处时,将在这里止裂。至此,这些原始微裂纹还不一定使岩石发生失稳,当外加荷载继续增加,已止裂且位于最危险方位的最大裂纹,将会沿基体再次发生扩展,导致岩体的宏观失稳断裂[3]。
当边坡岩体中的裂隙构造带由压应力占优势转为卸荷作用时,其开裂滑动过程将经历闭合摩擦滑动、压剪起裂,形成分支张型裂纹。新裂纹面顺最大主应力方向不断延伸发展直至位于分支张开型裂纹尖端的微裂纹区互相汇合,导致宏观裂纹的击穿贯通,从而导致裂隙的宏观开裂和滑动。起裂准则为[4]:
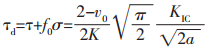
|
(1) |
式中:τd—剪切驱动力;
f0—岩体的剪切摩擦系数;
KIC—岩石的张型断裂韧度;
K—实验常数;
2a裂纹宽度;
σ—裂隙面正应力。
裂隙面的压剪起裂及分支扩展模型见图 3。
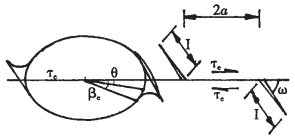 |
| 图 3 裂隙面的压剪起裂及分支扩展示意图 |
3 开挖卸荷对岩体强度的影响
将岩体三轴卸荷至受拉破坏,得到不同结构面夹角条件下试件的抗拉强度与结构面方向的关系[5] (见图 4)。由图 4可知,卸荷岩体的抗拉强度随着结构面方向的变化而变化。夹角较小时,抗拉强度较高; 随着夹角的加大,抗拉强度明显降低。当夹角α= 90°时,抗拉强度为0.3MPa,仅为未设置结构面岩石抗拉强度的1/13。这说明对于含有节理、裂隙的岩体,在卸荷作用下,其强度具有明显的各向异性的特点。
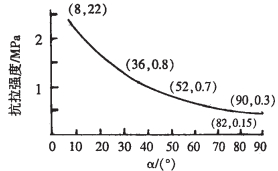 |
| 图 4 卸荷作用下结构面方向与抗拉强度关系 |
根据断裂力学理论,由于卸荷而产生张力,当裂隙尖端的张力强度过岩石的抗拉强度时,使得节理裂隙张裂扩展,这时裂隙间的摩擦系数大为减小。根据莫尔库仑理论:
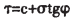
|
因裂隙表面正应力σ减小,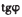
由线弹性断裂力学理论知,Ⅰ-Ⅱ复合型(即张剪型)裂缝端的应力强度因子,既有KⅠ又有KⅡ,KⅠ和KⅡ的组合情况随裂缝的长度、方位以及受力状态变化而变化。经过对弱风化岩石及微新岩石进行的Ⅰ-Ⅱ复合型断裂试验得到经验公式[6]如下:
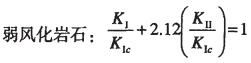
|
(2) |
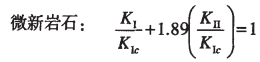
|
(3) |
上面两式左端小于、等于和大于1,分别对应裂缝稳定、临界状态和失稳扩展。从式(2)、(3)中可明显看到,由于卸荷下岩体中出现了张剪复合型破坏特征,使得岩体出现失稳的可能性大为增加。
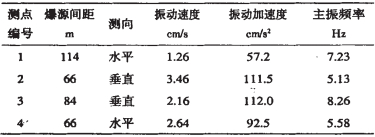
4 裂隙与振动应力的相互作用在正常生产开挖爆破条件下(2#岩石炸药,总药量3t,段药量150kg, 时差25ms),爆破振动引起边坡岩体质点振动的速度及加速度实测结果见表 3。另外,爆后现场观察表明,在靠近爆源的边坡表面,部分节理裂隙有张开扩展现象。
| 表 3 爆破振动部分实测参数 |
 |
| 点击放大 |
爆破振动所产生的动应力是以应力波的形式在岩体中传播的,当遇到节理裂隙面时, 以压缩波倾斜入射为例,应力波的反射、透射规律见图 5。
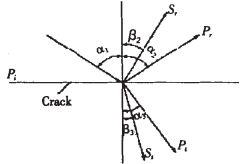 |
| 图 5 应力波遇到弱面时的作用机理 |
由图 5可知,以倾角α1人射的纵波Pi将产生4种波,即反射纵波Pr,反射横波Sr,透射纵波Pt,透射横波St。设c1、c2为纵波与横波在第一种介质中的传播速度; c3、c4为纵波与横波在第二种介质中的传播速度,则有[7]:
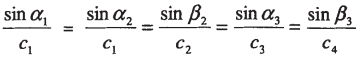
|
(4) |
对于纵波,其波动所产生的变形不存在旋转,因此,其运动方程可推导为:
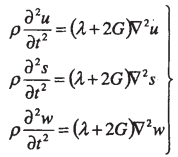
|
(5) |
设x轴为纵波的传播方向,则s=w=0, 而u仅是坐标x和时间t的函数,式(5)可简化为:
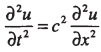
|
(6) |
方程(6)的通解可写为:
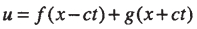
|
(7) |
当考察纵波沿x轴正向传播时,方程(6)的通解(7)可表示为:

|
(8) |
振动应力波入射到裂隙的交界面时,边界面质点要满足质点位移连续和应力连续条件,因此,在结构面的两侧,下列4种量必须相等[8]:
法向位移分量: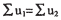
切向位移分量: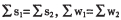
正应力: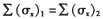
剪应力: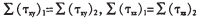
当振动应力波垂直人射到交界面时,只产生相应的透射纵波和反射纵波,应力大小与波阻抗的关系为:
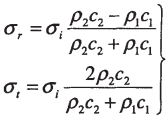
|
(9) |
式中σi—表示人射应力;
σr表示反射应力;
σt表示透射应力;
p1c1、p2c2表示l、2两种介质的波阻抗。
现把弱面分两种情况来分析:
(1) 弱面较宽,有与岩性差别很大的充填物。在这种情况下,一般来说充填物的波阻抗都小于岩体的波阻抗,即p1c1>p2c2,由式(9)可知反射应力σr为拉应力。拉应力很容易超过与充填物相交的岩石面的抗拉强度,从而引起充填物与岩石交界面处产生拉裂,形成开裂破坏。
(2) 弱面没有充填物时。当p1c1>p2c2时,由式(9)可知,在交界面处有反射拉应力产生,从而可能引起岩体沿弱面开裂破坏; 当p1c1>p2c2时,由式(9)可知,透射应力大于入射应力,由于岩体抗压强度较抗拉强度大许多倍,一般大10倍左右,所以不会因透射压力增大而引起岩体破坏。
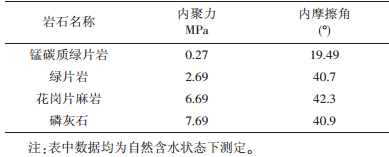
节理弱面处C、Ø值的大小及变化也是影响其开裂破坏的重要因素。在振动作用下岩体开裂破碎时,其开裂面主要位于岩体中的节理裂隙弱面处。一方面是因为弱面处的C、Ø值都远小于其它部位,黄麦岭露天边坡不同部位C、Ø值见表 4, 从表中可明显看到弱面处的C值比完整部位的降低约10~5倍,Ø值降低约1倍。另一方面,研究资料表明[9],内摩擦角与质点振速的关系为:
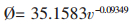
|
(10) |
| 表 4 部分岩体及弱面的C、Ø值 |
 |
| 点击放大 |
公式(10)说明, 振动速度越大,内摩擦角相应地降低越多,其破坏的可能性就越大。
5 结语针对实际工程得出了岩体边坡的应力应变分布规律,可供类似的露天岩体边坡在进行稳定性分析计算和边坡加固时参考。分形岩石力学是较新的研究领域,笔者将其用于岩体裂纹的扩展机理分析; 开挖卸荷对岩土边坡的影响机理,引起越来越多岩土工程师的关注,是值得研究的科研课题。
| [1] |
谢和平.
岩石分形力学[M]. 北京: 科学出版社, 1994: 255-306.
|
| [2] |
杨米加, 贺永年. 岩体裂隙结构模型及其渗流规律研究[J].
岩土力学, 1998, 19(4): 8–13.
|
| [3] |
Krajeinovie D, Fanella D. A micromechanieal damage model for concrete[J].
Eng.Fraet.Mech, 1986(25): 585–596. |
| [4] |
周维垣, 杨若琼, 剡公瑞. 岩体边坡非连续非线性卸荷及流变分析[J].
岩石力学与工程学报, 1997(16): 3:210–216.
|
| [5] |
李建林, 孟庆义. 卸荷岩体的各向异性研究[J].
岩石力学与工程学报, 2001(20): 3:338–341.
|
| [6] |
徐平, 夏熙伦. 花岗岩Ⅰ-Ⅱ复合型断裂试验及断裂数值分析叨[J].
岩石力学与工程学报, 1996, 15(1): 62–70.
|
| [7] |
刘北辰, 陆鸿森.
弹性力学[M]. 北京: 冶金工业出版社, 1986: 93-97.
|
| [8] |
李造鼎.
岩体测试技术[M]. 北京: 冶金工业出版社, 1993: 111-112.
|
| [9] |
朱传云, 赖世骧, 卢文波, 等. 爆破振动对岩体结构面影响的室内试验研究叨[J].
工程爆破, 1996(2): 51–54.
|
 2004, Vol. 18
2004, Vol. 18
