| 电除尘器中粉尘粒子的力学行为分析 |
在电除尘器中, 荷电尘粒因受到电场力的作用而趋向收尘极。当尘粒到达收尘极后, 粉尘受到多种作用力而沉积在收尘极上, 粉尘粒子是否重气流(即二次扬尘), 关键在于粒子受到的作用力, 即粒子之间的相互作用力(粘结力), 以及粒子与收尘极板表面之间的作用力(粘附力)。在电除尘器中, 粒子的粘结力对除尘有重要的现实意义, 如沉积粉尘层因粘结力过小而受到气流的切向冲刷、粒子的法向反弹或反向静电力的作用而发生返流; 或是因粘结力过大, 需要很强的振打才能将沉积的粉尘从收尘极板上震落下来。但此时, 却有可能使原来已形成块状的沉积粉尘层被击碎, 由此造成粒子返流量比常规振打时要大得多。在实际的收尘清灰过程中, 沉积粉尘粒子以单个粒子的形式落入灰斗是不可能的, 它只有通过粒子间的粘结力, 以块状、条状等形式才能达到收尘的目的。虽然人们在这方面做了大量研究, 但许多过程、现象仍然不能被人们很好地理解, 特别是收尘极板上粉尘粒子的力学行为, 例如沉降粉尘的二次扬尘仍然不能被清楚地描述和解释。因此, 深入研究电除尘器中粉尘粒子在电场中的运动以及分析收尘极板上沉积粉尘的受力状况, 对提高电除尘器的收尘效率具有重要的指导意义。
1 带电粉尘粒子在电晕电场中的运动 1.1 库仑力引起的偏转电除尘器对粉尘粒子的收尘过程是从离子使粉尘带电开始的。粉尘获得尽可能多的电荷是收尘过程最重要的前提。粉尘荷电包括两种荷电机理[1]:即碰撞荷电和扩散荷电。通过上述两种荷电机理荷电的粒子在电场强度为E0的收尘区域中, 受到库仑力Fe=qE0的作用向收尘极方向驱动, 这时粒子受到气流的斯托克粘性阻力为:
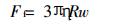
|
(1) |
式中:η—气体的粘性系数;
R—粒子直径, m;
w—粒子偏离气流的驱进速度, m/s。粒子受到的库仑力为:
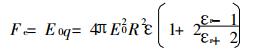
|
(2) |
粒子电场荷电的饱和荷电量q[1]为:
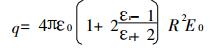
|
(3) |
式中:E0—未受干扰时的电场强度, V/m;
εγ—粒子的相对介电常数;
ε0—真空介电常数, F/m。
粉尘进入电除尘器时, 受到库仑力的作用而发生偏转, 以致粉尘粒子从气流中分离出来, 趋向收尘极板, 收尘是在库仑力Fe和粘性阻力Ff平衡的条件下进行的。
1.2 梯度力的影响在电除尘器中, 电场随位置变化时, 对电介质粒子会产生梯度力作用, 梯度力大小[2]可表达为:
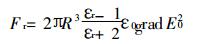
|
(4) |
即使粒子不带电, 也会受到梯度力的作用, 被吸引到电场场强强的地方。在电除尘器内部, 这个力将使粒子向放电极方向驱动, 并且在电场强度变化显著的放电线附近, 这个作用力很大。在这个力的作用下, 粉尘粒子会被电晕极吸附, 并且不断地在电晕极上堆积起来, 使放电线肥大, 抑制电晕电流, 妨碍收尘。为了防止这种不利现象的发生, 必须在电除尘器运行的过程中, 定时振打放电线, 震落附着在其上的粉尘粒子, 以保证正常的电晕放电。
1.3 离子风的影响在电晕放电的空间, 通常会产生离子风[3], 它是由于离子流和气体分子进行动量交换而产生的。这种风的方向和离子流的方向相同。但是当离子风到达收尘电极时, 就发生反转并通过离子流少的部分, 向放电线方向逆流, 于是, 收尘空间常常会被离子风扰乱。虽然离子风的风速并不大, 只有大约每秒几米的速度。但是对粒径很小的粒子, 由于库仑力产生的偏转速度(集尘速度、趋进速度)w很小, 所以, 离子风对粒径小于数微米的微细粒子的运动会产生很大的影响。也就是说, 粒子越小, 离子风的作用越大, 库仑力产生的收尘作用越弱。
1.4 粒子凝集粗大化虽然有上述离子风的影响, 但是由于微细粒子在电晕空间内部和收尘电极表面受到显著的凝集作用后会形成粗大粒子[4]。这时会受到较强库仑力的作用。所以电除尘器对微细粒子仍然有着很好的除尘作用。
通常, 粉尘粒子在静电场中会沿电场方向产生或大或小的极化, 出现极化电荷, 并在外部形成偶极子电场。如果把沿同方向极化的粉尘粒子放到它的附近, 这个粉尘粒子就会受到如图 1所示的沿电力线方向的力的作用。即该粉尘粒子将沿电力线方向移动, 并排在前者的上方或下方, 与其附着在一起。于是在很短的时间内, 就会使很多粒子沿电场方向连结在一起, 形成串珠形状, 如图 2所示, 这种现象叫串珠现象。不论粒子是否带电, 都会发生这种现象。所以, 在电除尘器中, 粉尘粒子在短时间内就会由于串珠现象而凝集粗大化, 这种现象不仅在电晕空间内部发生, 而且在收尘电极表面也会发生。所以, 使收尘电极在堆积的粒子层紧密地结合在一起的作用力, 就是粒子在收尘电极失去电荷后仍然保留的极化作用而产生的力。
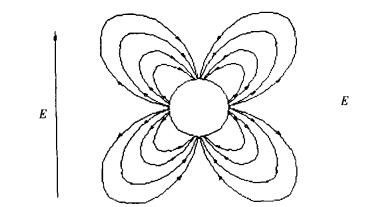 |
| 图 1 极化粒子对周围其他粒子作用的电场 |
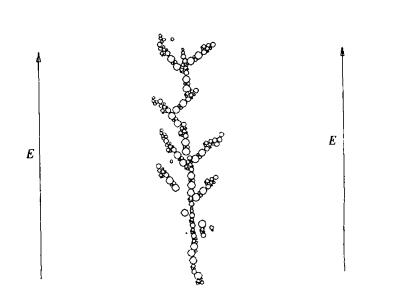 |
| 图 2 粉尘粒子在电场中形成串珠的现象 |
2 收尘极板上粒子受到的作用力
影响粉尘层粉尘粒子间粘结性能的力主要有范德华力(van der waals分子间的作用力)、库仑力(电荷间的作用力)、交联力(Ross -linking毛细作用而产生的表面张力)、静电引力(电位降产生的作用力)、电场力。
据文献[5]介绍, 在相对湿度超过50 %~60%时, 交联力随相对湿度增加而增大。因此, 当电除尘器电场内部温度很高时, 交联力被认为对粉尘粘结性能的影响很小。因此, 本文中忽略不计, 主要研究范德华力、静电引力、电场力。
2.1 范德华力范德华力的作用距离为10-8cm, 是在距离非常近的接触点之间的一种力, 设它的单位面积强度为U(N/m2), 作用距离为Z(m), 相互接触的粒子直径为R1和R2的两个球形粒子之间作用的范德华力Fv可以表示为:
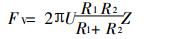
|
(5) |
若把R1或R2中的任意一个趋于无穷大, 则变成粒子和平板之间的情况。例如, R1变成无穷大, 由此可得粒子与平板电极之间的范德华力Fv为:
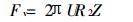
|
(6) |
为了把这个附着在收尘极上的单一粒子剥离, 假设需要振打的加速度为a:
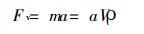
|
即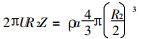
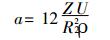
|
(7) |
式中:ρ—粒子密度, kg/m3。
式(7)表明:粒子越大, 需要的振打加速度越小; 粒子越小, 需要的振打加速度越大, 当振打加速度增大并且达到使微细粉尘振落时, 会产生二次扬尘, 在实际的电除尘器应用中, 应选择适当的振打加速度。因此, 微细粉尘粒子不易被振落, 范德华力起了一定的作用。
2.2 静电引力当粉尘表面产生电容时, 由于接触电阻, 粉尘间电流引发电位下降, 产生了静电引力, 假设粉尘粒子是球形的, 建立数学模型如图 3。
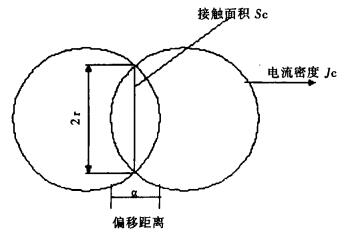 |
| 图 3 静电引力数学模型 |
利用hert'z接触理论公式[6], 偏移距离为:
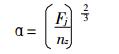
|
(8) |
接触电阻Rc:
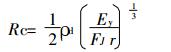
|
(9) |
接触电阻Rc通过偏移距离来描述接触表面电阻ρc:
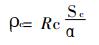
|
(10) |
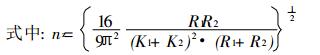
|
(11) |
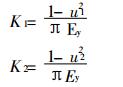
|
K1和K2是与物质的杨氏模量Ey、泊松比μ有关的变量。
所以静电引力表达式如下[7]:
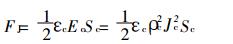
|
(12) |
式中:ρc—粒子接触表面比电阻, Ω·cm;
ρd—粉尘比电阻;
r—接触半径, m;
Sc—接触面积, m2;
Ec—接触面场强, v/m;
Jc—接触面的电流密度, A/m2;
εc—接触面的介电常数, F/m;
Ey—杨氏模量, 约为7×1010Pa;
μ—泊松比, μ1=μ2=0.14。
通过对粉尘层静电引力分析得出, 粒子接触电阻和电流密度越大, 静电引力越大。由于静电引力作用, 粒子更容易粘结在一起, 形成大粒子(甚至形成条状或块状的粉尘团)。这就意味着粒子间的静电引力有利于振打。同时, 粒子与极板间也有很小的静电引力, 因此, 一些附着在收尘极板的微细粉尘粒子很难振打下来。
2.3 电场力当粉尘粒子到达收尘极板后并沉积在收尘极板上, 形成粉尘层, 随着粉尘层增厚, 渐渐地在粉尘层内部形成了场强为Ed的电场[8], 这时产生的电场力Fm为:
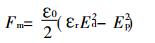
|
(13) |
式中:Ed—尘层内部场强, V/m;
Ep—收尘空间场强, V/m。
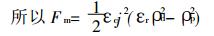
|
(14) |
式中:J—电流密度;
ρd、ρp—分别为粒子层和收尘空间的比电阻。
当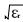
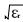
在电除尘器中, 收尘空间的比电阻ρp约为1010~ 1011Ω·cm; 另外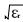
以上所讨论的粘结力对粉尘的收集、电除尘器的振打系统及方式起着重要的作用。
2.4 讨论以上是对某种力进行单独分析而得出某种单个力对粉尘粒子的作用, 实际上, 以上各种力之间存在着相互作用, 其结果可能起加强的作用或起减弱的作用。并且, 很多条件是在理想状态下进行分析的, 与实际情况会有一定的偏差。
3 结论本文通过对范德华力、库仑力、交联力、静电引力、电场力研究, 从理论上得出收尘极板上粉尘粘结的种类和大小以及影响因素。
(1) 在静电引力的计算中, 静电引力随粉尘比电阻增大而增大, 这就意味着:粉尘间粘结力、粉尘与极板间的粘附力也随比电阻增大而增大, 粉尘比电阻是影响粘结力大小的一个重要因素;
(2) 电场力受电场、粉尘比电阻的影响, ρd←1010 Ω·cm范围内时, Fm为剥离力, 只有当ρd 1010 Ω·cm时, 电场力Fm才表现为附着力;
(3) 当电场力增大, 并且超过范德华力、静电引力总和时, 粉尘就会从收尘极板上进入气流中, 这就意味着直径很小(大约100μ m)或更小时, 粉尘离子就会反弹进入气流中, 在这种情况下, 范德华力可以忽略, 这就看电场力和静电引力是否平衡, 当电场力继续增大, 超过静电引力, 就可以认为此时粒子受到的粘结力为零, 粒子间发生分离是由于粘结力的消失, 而不是粒子和附着面的破碎。
| [1] |
黎在时.
, 静电除尘器[M]. 北京: 冶金工业出版社, 1993: 11-20.
|
| [2] |
解广润.
高压静电场[M]. 上海: 上海科学出版社, 1983: 50-142.
|
| [3] |
肖福春. 电风对粒子静电收集性能的影响[J].
南方冶金学院院报, 1993(2): 87–93.
|
| [4] |
师华. 静电除尘装置中粉体粒的荷电性质和力学行为[J].
静电, 1994(1): 6–7.
|
| [5] |
Yoshihiko Mochizuki ELECTRAL RE -ENTRAINMENT OF PA RTICLES DEPOSITED ON COLLECTING PLATE IN ELECTROSTATIC PRECIPITATOR[D].Presented at the 8th internationaI conference on EIectrostatic Precipitation May 14-17, 2001 1-2.
|
| [6] |
Didier BIanchard, Pierre Atten CorreIation between current density and Iayer structure for fine particIe deposition in a Iaboratory eIectrostatic precipitator[J].IEEE transactions industry appIications VoI, 38 No 3 may/june2002, 833 -834.
|
| [7] |
K J. McLean Cohesion of precipitated dust Iayer in eIectrostatic precipitators[J].
APCA J, 1997, 27(11): 1100. |
| [8] |
周永安, 收集低比电阻粉尘极板结构的探讨[A], 第三届中国物理学会静电专业委员会静电学术报告会论文集[C], 浙江诸暨: 1987. 274 -275.
|
 2003, Vol. 17
2003, Vol. 17
