| 剪切机的运动学分析 |
某厂使用的剪切机主要用于剪切圆形不绣钢材, 其原为一种手工剪切工具。为了满足和适应工作需求以及进一步提高生产效率, 将其改造为一种自动剪切装置。现就这一自动剪切装置进行最小和最大剪切性能分析。
1 装置简介该剪切装置如图 1所示, 它主要由调速电机、皮带轮、减速器、圆盘、联杆、机架、剪切机等组成。
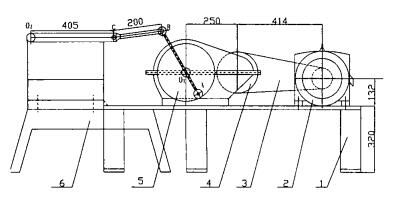 |
| 1.机座; 2.调速电机; 3.皮带; 4.减速器; 5.圆盘; 6.剪切机 图 1 剪切机工作原理装配图 |
该剪切装置的工作原理是:调速电机输出功率经皮带减速和减速器减速后将扭矩输入到减速器的低速轴, 该轴与圆盘一起作同步等速圆周运动。
圆盘与联杆AB在A点联结, AB与BC在B点联结, O2C为剪切机的刀架。联杆AB在圆盘的带动下作平面运动, BC在AB的带动下也作平面运动, O2C在BC的带动下绕O2轴作小圆弧圆周运动, 从而带动剪切刀片作上下垂直运动, 完成剪切需求。有关技术参数如下:
(1) 调速电机初步选为JZT22-4, n=120~1200r/min, P=1.5kW;
(2) 三角皮带减速比为i1=2, 传动效率η1= 93%, 减速器为JZQ250-ⅠX-ⅡZ, i2=8.23, 传动效率η2=97 %;
(3) 圆盘中心O1到与AB联杆联结处的A点距离为130mm, 联杆AB为400mm, 联杆BC为200mm, 二联杆为直径f10mm、HT15-33的圆柱杆件材料。刀架O2C为405mm的方形杆件, 与剪切刀片一起运动完成剪切, 质量共约为15kg。联杆BC与刀架O2C为圆柱齿轮联结, 相互啮合并随刀架绕O2轴作平面复合运动。
(4) 由于受传动效率和摩擦等因素的影响, 假设调速电机的功率用于剪切某型号钢材的总效率为70%, 即有30%的电机率用于摩擦和传动消耗。
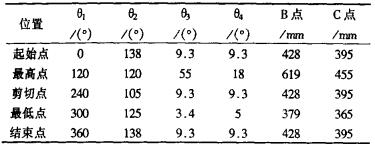
2 运动分析机构运动分析的方法很多, 主要有图解法和解析法。图解法具有形象直观和简单的特点, 对于一般精度的机构可以满足分析要求, 因此比较常用。笔者即采用CAD结合图解法对该装置进行运动分析。通过剪切试验可得该装置具有一定的运动规律。记录下各位置点的数据如表 1, 其中θ1, θ2, θ3, θ4分别为联杆O1A, AB, BC, O2C在A, B, C, O2点处与坐标轴X轴正方向的夹角, B点和C点的高度为距离机架水平面的垂直距离。
| 表 1 剪切机运动位置参数表 |
 |
| 点击放大 |
分析该试验数据可知在一个周期内, 起始点、剪切点和和结束点的运动位置完全重合, 且此时B点和C点的水平夹角均相等, 即刀架O2C和联杆BC在一条直线上, 具有相同的瞬时运动规律。根据这一运动特性, 可画出开始剪切瞬时的机构运动简图, 如图 2。
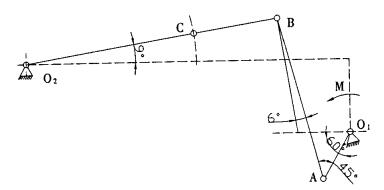 |
| 图 2 机构运动简图 |
2.1 速度分析
已知条件:lO1A=130mm, lAB=400mm, lBC= 200mm, lO2C=405mm, 并假设此时调速电机转速为n=1 200r/min。根据以矢量方程图解法求解机构上某点速度的步骤及已知条件, 并根据机构运动简图可画出剪切瞬时的机构运动速度矢量图, 如图 3所示。
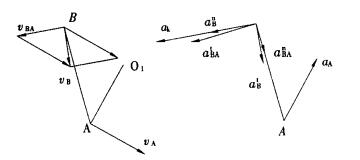 |
| 图 3 机构运动速度和加速度夭量分析 |
A点速度分析如下:
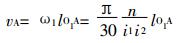
|
(1) |
代入数值得vA=1.0m/s, 方向如图所示, 大小与电机转速成正比。
B点速度由速度三角形可得:
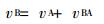
|
(2) |
根据投影关系, 可得vB=0.71m/s, 同理可得vBA=0.78m/s, 方向均如图所示。由于机构运动的特殊关系, 此时O2C和BC在一条直线上, 所以ωO2C=ωB=1.17rad/s, 方向为顺时针。同理可得ωBA= 1.95rad/s, 方向为逆时针。
以上为开始剪切瞬时的运动速度, 当剪切达到最低点即B点和C点分别位于最低点瞬时(图略), 根据式(2)可得vB=0, vBA=vA=1.0m/s, 方向与vA相反, 同理可得此时vC=0, 所以联杆作瞬时平动并通过C带动O2C作小圆弧运动。
2.2 加速度分析同理, 可画出开始剪切瞬时的机构运动加速度矢量图, 如图 3所示。所以B点加速度关系具有下式:
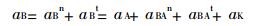
|
(3) |
上式中:
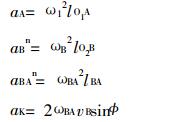
|
分别代入所需数值得:
aA=7.58m/s2, 与电机转速平方成正比, 方向图示;
aBn=0.83m/s2, aBn、aBt的方向图示;
aBAn=1.52m/s2, aBAn、aBAt的方向图示;
aK=2.76m/s2, 方向图示。
因(3)式中只有aBt、aBAt的大小未知, 故可以求解。根据投影关系可解得:aBt=3.78m/s2。O2C绕O2轴运动的角加速度为:
ε1= aBt/lO 2B=6.25rad/s2, 顺时针方向。
当剪切达到最低位置(即B点和C点分别位于最低点)时, 由以上分析可知此时BC作瞬时平动。根据反复试验可得此时O2C绕O2轴运动的角加速度ε2小于剪切开始时的角加速度ε1。
3 受力分析采用隔离体分析法对该装置进行瞬时机构受力分析, 如图 4所示。
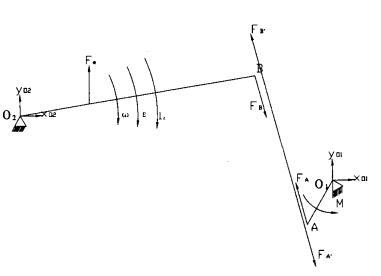 |
| 图 4 机构运动受力分析简图 |
图 4中, M为调速电机的转矩, 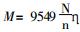
对O1点取矩得:
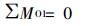
|
即:
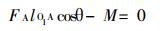
|
(4) |
由(4)式代入数值得:FA=1496.0N, 方向如图所示。
对O2点取矩得:
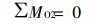
|
即:
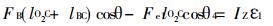
|
(5) |
上式中FB=FA, Fe1为假设的剪切阻力, 受力方向图示。IZ为联杆O2C和CB绕O2轴转动的转动惯量, 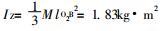
综合以上条件, 代入数值得Fel=5005.0N。当剪切达到最低点时, 由于ε2 < ε1, 根据式(5)得Fe2> Fe1。
假设此时剪切钢材为1Cr18Ni9Ti, 直径为d, 其剪应力τ=120MP。由公式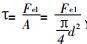
由以上分析计算可得, 当调速电机转速为n= 1200r/min时, 可以剪切的最大直径为7mm。由于电机转矩和作用于剪切机上的受力与转速成反比, 剪切机的剪切速度与转速成正比, 剪切加速度与转速平方成正比, 因此当电机转速降低时, 能够剪切的钢材直径将更大。该自动剪切机在设计时其功率要求是能够剪切1Cr18Ni9Ti不绣钢材的直径为4mm, 通过以上分析可得该剪切设备具有一定的冗余性能, 完全符合当初设计需求。
| [1] |
《机械设计师手册》编写组. 机械设计师手册[M]. 北京: 高等教育出版社, 1998.
|
| [2] |
傅祥志.
机械原理[M]. 武汉: 华中科技大学出版社, 2000.
|
| [3] |
曹惟庆.
机构设计[M]. 北京: 机械工业出版社, 1993.
|
| [4] |
孙新民.
现代设计方法[M]. 北京: 人民邮电出版社, 1999.
|
| [5] |
刘鸿文.
材料力学[M]. 北京: 高等教育出版社, 1997.
|
 2003, Vol. 17
2003, Vol. 17
