| GA-BP算法及其在冰铜品位神经网络模型中的应用 |
当前已有的诸多人工神经网络中, 多层前向网络是在实际中应用最广泛的一类[1]。由于传统的神经网络训练算法, 即BP算法[2], 存在着收敛速度慢和可能陷入局部极小点两大弱点, 学习算法的改进一直是神经网络研究的一个重要方向。一般而言, 可以采取调整学习步长、改变动量系数等措施来加快BP算法的收敛速度[3], 但为了克服局部收敛, 则必须彻底摆脱依赖梯度信息来指导权值调整方向的计算方法。遗传算法是一种随机的优化与搜索方法, 算法搜索轨道有多条, 具有良好的并行性、全局优化性和稳健性[4]。遗传算法与BP算法之间存在着很大的优势互补, 于是可将它们有机地结合起来, 形成一种快速全局搜索算法。将该算法应用于冰铜品位神经网络模型的训练, 结果表明该算法优于BP算法。
1 BP算法及其缺陷BP算法是目前应用最普遍的一种神经网络训练学习方法, 其实现过程可描述如下:
(1) 给全部权值和阈值赋予较小的随机值;
(2) 从学习样本中取出一个输入样本, 计算出神经网络的输出值;
(3) 给出期望的输出值, 计算所有层的局部误差;
(4) 用迭代公式修改各层的权值和阈值;
(5) 取下一样本, 重复(2)、(3)、(4), 若样本已完, 进入(6);
(6) 计算平方误差或最大误差ξ, 若ξ小于给定的较小值ε或训练次数大于给定的最大训练次数, 则停止; 若ξ>ε, 则返回(2)。
在实践中BP算法暴露出自身的弱点, 最为突出的就是收敛速度慢和可能陷入局部极小点的问题。BP算法中的核心部分, 即权值系数的调整迭代公式:
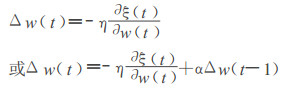
|
其中ξ为平方误差, Δw(t)和Δw(t -1)分别为t和t -1时刻的权值调整值, η为学习步长, α为动量系数。
从迭代公式可以找到BP算法问题存在的根源。BP算法实质上是采用优化运算中的梯度下降算法, 是一种局部寻优算法, 它利用误差对于权值系数的一阶导数信息来获取下一步的权值调整的方向, 以求最终达到误差最小。为了保证算法的收敛性, 学习步长η必须小于一个上限, 这就导致了BP算法收敛速度慢的问题, 并且越是接近极小值处, 算法的收敛速度就越慢。而由于实际问题的求解空间往往是极其复杂的多维曲面, 并且存在很多局部极小点, 所以BP算法陷入极小点的可能性就很大。这也就使得网络权值的初始取值对训练结果有很大的影响。通过随机设置的初始权值经训练往往达不到全局最优点。
2 GA-BP算法及其流程遗传算法(Genetic Algorithms, 简称GA算法)是基于自然选择和自然遗传这种生物进化机制的搜索方法, 把优化问题的解的搜索空间映射为遗传空间, 现已发展成为一种自适应启发式概率性迭代式全局搜索算法。用GA算法求解问题通常包括以下步骤:
(1) 编码:选择一定的编码策略(如二进制编码), 将待优化参数用有限长的数字串来表示, 即形成染色体, 每一个染色体代表问题的一个解, 即个体。染色体上的每一位称为基因。
(2) 初始化群体:随机产生n条染色体组成初始群体。
(3) 计算适应度:根据定义的适应度函数F=f (x), 计算群体中每个个体的适应度。适应度反映了个体之间的相对优劣程度。
(4) 选择(复制):根据复制概率选择染色体进行复制, 适应度高的染色体被复制的概率大, 适应度低的染色体被复制的概率小, 从而保证了物种的进化。
(5) 交叉:随机配对选出杂交母体, 在染色体上随机选择位置进行交叉换位。
(6) 变异:以一定概率的方式将染色体上的某位基因进行逆变, 以模仿生物中基因突变。变异也正是遗传算法实现全局寻优的重要手段。
(7) 重复(3)至(6), 直到最优个体的适应度达到某一给定值, 或最优个体和群体的平均适应度不再提高。
GA求解过程本质上是随机寻优过程, 不存在局部收敛的问题, 但GA依据概率随机进行的寻优操作在多数情况下只能得到全局范围的次优解, 获得最优解也比较难, 这是因为这种寻优搜索是随机的, 带有一定程度的盲目性。
所以, 可以将GA和BP算法相结合, 形成一种兼有两者优势的算法—GA-BP算法, 此算法将遗传算法的全局寻优能力与BP算法的指导性搜索思想相结合, 既克服了寻优中的盲目性, 又避免了局部收敛情况的发生。该算法的神经网络学习流程如图 1所示。
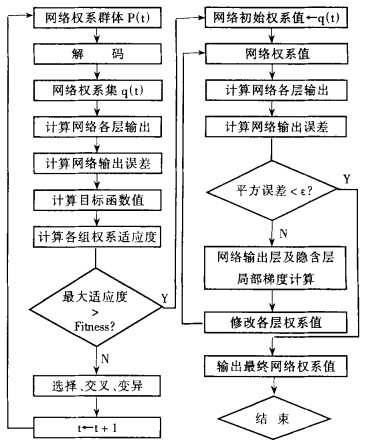 |
| 图 1 遗传BP算法网络学习流程图 |
遗传BP算法对权值进行[-1, 1]范围内的二进制编码, 初始化产生由n条染色体组成的群体P(0)后, 进行反编码(即解码), 得到n组网络权系, 对每组权系按下式进行适应度计算:
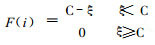
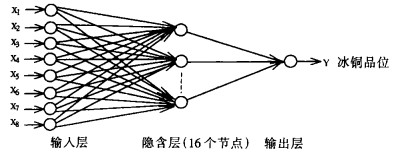
闪速炉炼铜中的冰铜品位神经网络模型如图 2所示。输入层由富化率、吨矿氧量、熔剂率、Cu含量、S含量、Fe含量、SiO2含量和MgO含量等8个节点组成, 输出层只有冰铜品位1个节点, 隐含层节点数为16。训练样本数为50(1到50号样本), 检验样本数为10(51到60号样本)。
 |
|
x1为富化率;x2为每吨矿含氧量;x3为熔剂率;x4为Cu含量; x5为S含量;x6为Fe含量;x7为SiO2含量;x8为MgO含量 图 2 冰铜品位神经网络模型示意图 |
GA -BP算法和纯BP算法对此模型的训练与检验结果分别如图 3和图 4所示。由图可知, GABP算法对训练样本的拟合效果(即挖掘样本间隐含规律的能力)和对检验样本的回响效果(网络的泛化能力), 都较纯BP算法好。训练中还发现, 纯BP算法每次的训练效果都有所波动, 时好时坏, 而GABP算法较稳定。这也正说明了BP算法随机初始权值的影响性和遗传算法全局预搜索的有效性。
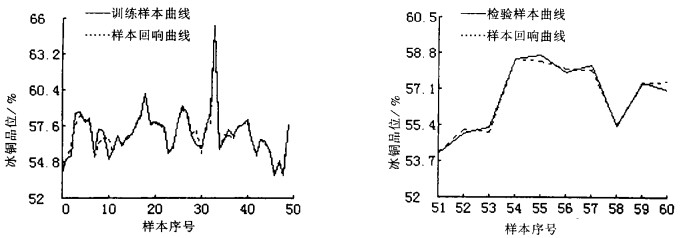 |
| 基于BP算法的冰铜品位神经网络模型训练与检验结果 图 3 基于GA-BP算法的冰铜品位神经网络模型训练与检验结果 |
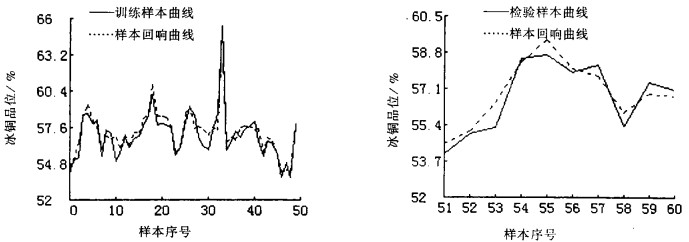 |
| 图 4 基于BP算法的冰铜品位神经网络模型训练与检验结果 |
图中数据也说明, 冰铜品位神经网络模型具有较强的挖掘样本间隐含规律的能力, 对训练样本的拟合效果较好, 同时对检验样本的响应效果良好, 模型泛化能力强, 即神经网络技术应用于铜闪速熔炼过程建模是可行的, 也是有效的。
4 结语在分析了BP算法缺陷根源的基础上, 提出将遗传算法的全局寻优能力与BP算法的指导性搜索思想相结合, 形成了GA -BP算法。对冰铜品位神经网络模型的训练和检验结果比较表明, 该算法优于BP算法, 既避免了BP局部收敛情况的发生, 又克服了GA寻优过程中的盲目性, 是一种快速全局搜索算法。模型训练结果也说明了神经网络技术应用于铜闪速熔炼过程建模的可行性和有效性。
| [1] |
李士勇.
模糊控制.神经控制和智能控制论[M]. 哈尔滨: 哈尔滨工业大学出版社, 1998: 91-93.
|
| [2] |
张乃尧, 阎平凡.
神经网络与模糊控制[M]. 北京: 清华大学出版社, 1998: 12-16.
|
| [3] |
Haykin S.
Neural Networks, A comprehesive Foundation[M]. Macmillan colla ge publishing company, 1994.
|
| [4] |
周明, 孙树栋.
遗传算法原理及应用[M]. 北京: 北京国防工业出版社, 1999: 18-24.
|
 2003, Vol. 17
2003, Vol. 17
