| 铝锭堆垛机械手的运动学分析及其仿真 |
铝锭的搬运和堆垛是电解铝行业中不可缺少的一种作业方式, 堆垛作业的劳动强度大, 且常常是在高温环境下工作。在传统的铝锭堆垛作业中, 最常见的堆垛作业流程为:浇铸→输送→脱模→冷却→提升→(翻转)→整齐→夹持→提升→(换向)→堆垛。这种堆垛作业方式工序流程长, 所需使用的设备多, 且占用空间大, 堆垛效率低。所以有必要设计一种占地面积小、作业范围大、堆垛效率高和便于操作的堆垛机械手来完成铝锭的堆垛作业。
1 运动系统的建立铝锭的外形与尺寸如图 1所示。其堆垛作业要求为:①一垛为11层, 第一层为4块, 其余各层为5块。②相邻两层交错放置。③第一层4块宽面朝上放置, 其余各层中的相邻两块铝锭均按正反向方位放置。
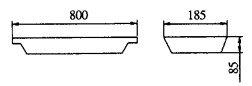 |
| 图 1 铝锭外形尺寸图 |
根据以上堆垛要求, 可知机械手在堆垛时需要完成的动作见图 2。
 |
| 图 2 机械手工作循环图 |
由此而建立的运动系统如图 3所示。采用图 3的运动系统可使机械手具有:夹持、上举、放下、伸缩、摆动及翻转定向的操作机能。其中夹持和翻转动作由手部来实现。
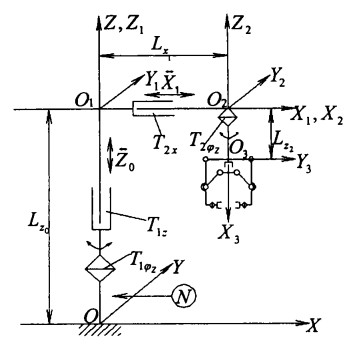 |
| 图 3 机械手运动系统图 |
2 运动学分析 2.1 机械手手部运动方程的建立
如图 3所示的运动系统, 设手部的起始位置在ZOX面上。机身在Z轴上。当机身转动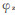
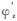
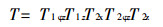
|
(1) |
其中:
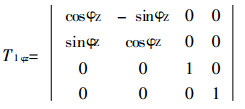
|
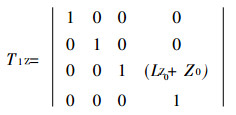
|
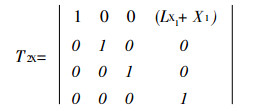
|
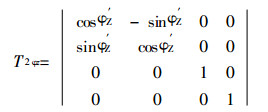
|
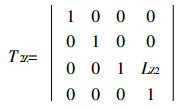
|
运动学分析就是在不涉及力和力矩情况下, 建立运动系统的运动方程, 来分析机械手的手部对基座坐标系的运动变化规律及参数。而正运动学就是给定各关节的转角、移动量, 来求手部的位姿。
公式(1)即为堆垛机械手手部的位姿变换矩阵, 即:
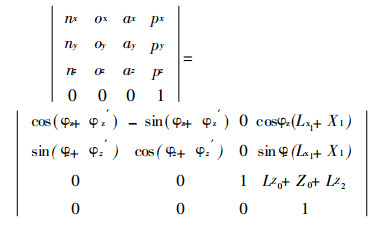
|
(2) |
式中:nx、ny、nz—分别表示手部法向矢量在基坐标系中X、Y、Z轴上的投影;
ox、oy、oz—分别表示手部方位矢量在基坐标系中X、Y、Z轴上的投影;
ax、a y、az—分别表示手部接近矢量在基坐标系中X、Y、Z轴上的投影;
px、py、pz—分别表示手部位置矢量在基坐标系中X、Y、Z轴上的投影。
由式(2)可得到手部相对于基坐标的位姿, 正运动学问题得到了解决。式中px、py、pz 3个位置元素为:
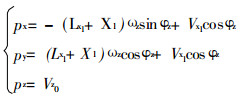
|
(3) |
手部的速度方程, 可由式(3)中的px, py, pz坐标分量对时间t的一阶导数求出, 即:
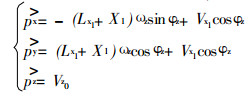
|
(4) |
手部的加速度方程, 可由式(3)中的px, py, pz坐标分量对时间t的二阶导数求出, 即:
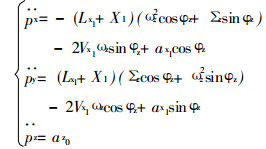
|
(5) |
式中: 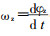
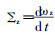

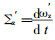
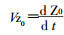
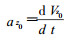
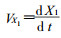
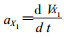
X1———手臂的X向伸缩长度;
Z0———机身的Z向升降距离;
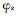
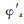
LX1———手臂的最小臂长;
LZ2———手腕的长度;
LZ0———机身的最小高度。
2.3 逆运动学分析逆运动学分析就是给定手部的位姿, 来求各关节的转角、移动量。
在逆运动学分析中, 公式(1)的左边矩阵T为已知的位姿矩阵, 等式右边矩阵中的元素是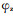
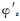
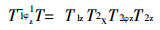
|
(6) |
由式(6)可得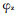
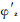
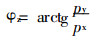
|
(7) |
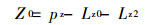
|
(8) |
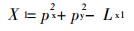
|
(9) |
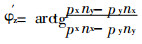
|
(10) |
正运动学模拟仿真是已知各关节的运动情况, 求机械手手部的运动情况。首先按照机械手各杆件的长度数据建立相应的数学模型, 然后输入各个关节的运动状态(
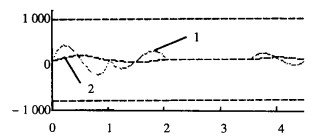 |
| 1.速度;2.加速度 图 4 速度、加速度曲线 |
3.2 逆运动学模拟仿真
机械手逆运动学仿真是已知机械手手部的位姿, 求各关节的运动情况。在铝锭堆垛机械手逆运动学仿真中, 先输入手部期望的位置值px, py, pz, 然后根据公式算出相应的
(1) 通过对堆垛的作业要求进行分析, 确立了4自由度铝锭堆垛机械手的运动系统, 建立了相应的运动学模型, 并对其进行了模拟仿真, 可以非常直观地了解铝锭堆垛机械手各关节的速度和加速度变化情况。
(2) 建立的运动系统所研制的堆垛机械手, 作业空间大, 占地面积小, 各运动关节相互独立, 易以控制, 可以满足铝锭堆垛作业要求。
(3) 所建立的堆垛机械手运动学模型, 还可推广到其他有色、冶炼和冶金行业的堆垛作业。
| [1] |
蔡自兴.
机器人学[M]. 北京: 清华大学出版社, 2000.
|
| [2] |
周建华.
MATLAB5.3学习教程[M]. 北京: 北京大学出版社, 2000.
|
 2003, Vol. 17
2003, Vol. 17
