| RBF神经网络在选矿生产指标预测模型中的应用 |
神经网络在矿业工程中的应用是从20世纪90年代才开始的, 主要用于水力旋流器、磨矿回路、浮选回路、碳金浸出过程、试验研究这几个方面非线性建模及控制。采用的神经网络一般为多层前馈的BP神经网络, 但BP神经网络存在局部最优问题, 并且训练速度慢、效率低, 而RBF神经网络在一定程度上克服了这些问题, 它在逼近能力、分类能力和学习速度等方面均优于BP神经网络。现根据某选矿厂流程查定结果, 随机取样得到的数据, 应用RBF神经网络对选矿生产指标进行预测, 建立相应的RBF神经网络预测模型。
1 RBF神经网络的结构及其特性假设x、x0∈RN, 以x0为中心, x到x0的径向距离为半径形成的||x-x0||构成的函数系{k(x) =O||x-x0||}称为径向基函数。RBF神经网络是一种前向网络的拓扑结构, 具有两层网络:隐层和输出层, 如图 1所示。第一层是隐层, 该层的变换函数是非线性传递函数, 常用高斯核。其第i个隐单元对应的输出为:
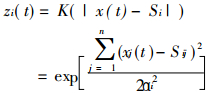
|
(1) |
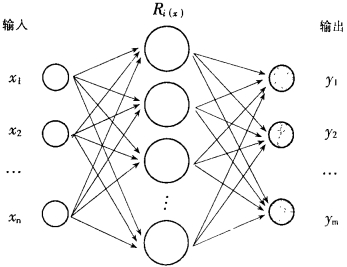 |
| 图 1 径向基RBF神经网络 |
式中:zi(t)第i个隐单元的输出;
x(t)第i个输入模式矢量;
Si隐层中第i个单元的变换中心矢量;
ai对应第i个中心矢量的标准化参数(也称形状参数)。
径向基函数的输出随输入和变换中心矢量之间的距离减少而增大, 则隐单元的作用相当于对输入模式进行一次变换, 将低维的模式输入数据变换到高维空间, 此过程实际上可以看作是对输入数据进行特征提取。对于输出节点yj(t), 有
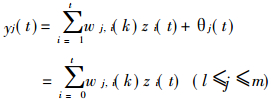
|
(2) |
式中: m输出节点数;
l隐层节点数, wj, 0(k) =θj(k), z0(t) = 1。
网络的输出层节点是线性处理单元, 对输入模式具有很好的分类特性。假设dj(t) 为第t个模式、第j个节点的期望输出, 则误差目标函数为:
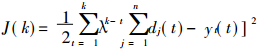
|
(3) |
式中:λ加权因子, 0 < λ < 1。
2 RBF网络的训练方法正交最小二乘法OLS简单易行, 运行速度快, 可避免局部最优问题, 是目前训练RBF网络的常用方法。该算法首先选择充分多的实际输入数据点作为初始RBF中心, 并根据所有RBF应当覆盖这个输入区域的原则, 确定其半径, 从而预先确定了每一个RBF的形式, 然后应用子集回归的观点, 应用Gram-Schmidt正交化过程, 从上述已确定的RBF中选择对网络性能影响相对较大的一部分RBF构成最终的网络。该系统的网络也采用OLS法进行训练, 对训练好的网络模型可以进行预测输出。
3 浮选技术指标预测模型RBF网络一般有监督学习网络, 设计网络时应有相应的输入训练样本和输出目标样本。一般地, 输入样本P为n×k的矩阵, n是单样本输入向量的维数, 用来表征待处理事物的输入特性, k是输入的训练样本数; 输出样本T为m×k的矩阵, m是单样本输出向量的维数, 用来表征待处理事物输出目标特性, k是输出的训练样本数。
现以某铅锌选厂为研究对象, 选用铅、锌精矿品位和作业回收率为考察变量。浮选技术指标与原矿铅品位、原矿锌品位、石灰用量、丁黄药用量、乙硫氮用量、Ps用量、硫酸铜用量和2#油用量等8个变量有关。因此RBF模型以上述8个变量为神经网络的输入, 即n= 8;以铅、锌精矿品位和铅、锌精矿回收率为神经网络的输出, 即m= 4;在该选厂某一段时间的流程查定结果中随机取样, 共取得有效样本k= 150个, 其中10个检验样本。在网络进行训练时, 隐含层的神经元数量为140。
系统软件在MATLAB环境中开发[1], 将样本数据输入网络进行训练, 得到网络的权值和阈值矩阵, 即系统的指标预测知识库, 然后根据检验样本进行指标预测。浮选指标预测模型功能示意图见图 2所示。
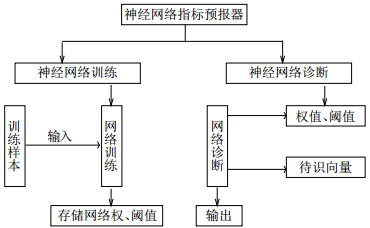 |
| 图 2 浮选指标神经网络预测模型 |
所有的训练均在AMDK6(TM)/350 CPU PC机上进行。当迭代进行到1 200次后, 系统误差基本稳定在10-2, 已经完全满足设计或实际的要求, 如图 3所示。与BP神经网络相比, RBF神经网络在很短时间内即可达到误差要求, 训练速度较快。为了检验所训练的神经网络的抗干扰能力, 分别对10个检验样本的输入进行了检验。通过仿真运算发现, 该网络的仿真值与实际值很接近, 如图 4~7。
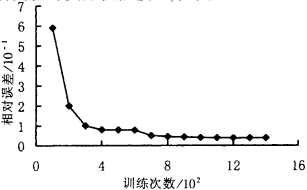 |
| 图 3 相对误差随训练次数的变化曲线 |
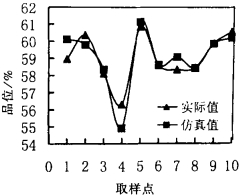 |
| 图 4 铅精矿品位仿真结果 |
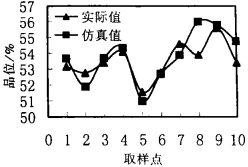 |
| 图 5 锌精矿品位仿真结果 |
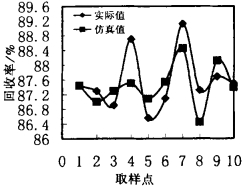 |
| 图 6 铅回收率仿真结果 |
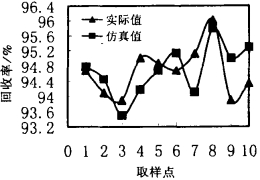 |
| 图 7 锌回收率仿真结果 |
4 结论
(1) 采用人工神经网络方法建立了浮选指标的RBF算法模型。用该模型得到的仿真值和实际值基本吻合。该模型预测精度高、误差小, 且具有较强的抗干扰能力和稳定性, 具有一定的实用价值, 为下一段开发选矿专家系统奠定了基础。
(2) RBF神经网络是一种性能良好的前向网络, 它不仅具有全局逼近性质, 而且具有最佳逼近性能。同时RBF神经网络在结构上具有输出)权值线性关系, 训练速度快, 不存在局部最优问题。从实际分析结果来看, 该网络可成功应用于浮选过程的指标预测, 对选别生产过程有一定的借鉴意义。
| [1] |
温新, 周露, 王丹力, 等.
MATLAB神经网络应用设计[M]. 北京: 科学出版社, 2001.
|
 2002, Vol. 16
2002, Vol. 16
