| 矿山岩爆机理的探讨 |
2. 中南工业大学, 湖南 长沙 410083
2. Central South University of Technology, Changsha 410083, Hunan, China
岩爆是地下工程中常发生的复杂的动力失稳现象。近年来, 随着矿山开采的数量、规模及其深度日益增长, 矿山发生岩爆的现象越来越突出, 人员伤亡和财产损失也愈来愈大〔1~3〕。为了更好地预防预报这一类岩爆的发生, 首先要分析这一类岩爆产生的原因, 笔者曾对此做过较详细的分析与研究〔3〕; 然后对其机理再加以研究。为此, 对这一类岩爆的机理进行了探讨。
1 模拟矿山岩爆现象力学模型的建立众所周知, 岩爆就是由于地下工程的开挖(或开采), 使得岩石所受应力重新调整, 产生应力集中, 当应力达到某一临界值时, 岩石发生突然破坏, 产生岩爆; 从能量的角度来看, 岩石内部贮存了巨大的弹性应变能, 一旦扰动, 弹性能突然释放, 使得破坏的岩石获得足够的动能, 而发生岩爆。国内外几个矿山发生岩爆的情况如表 1所示。
| 表 1 世界各国矿山发生岩爆的情况 |
 |
| 点击放大 |
就矿山而言, 矿柱就相当于试件, 顶底板就相当于试验机的上下压板, 如图 1所示。换句话说, 矿柱就是一种矿山结构, 顶底板就是一种矿山结构负荷系统。因此, 当矿柱中的平均压力超过其抗压强度极限、加以顶底板的刚度小于矿柱的刚度时, 此时矿柱将发生突然破坏, 产生岩爆。这一现象具有普遍性, 为此提出并建立一个与之相似的力学模型。
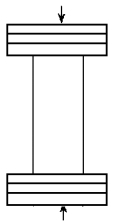 |
| 图 1 岩石的单轴压缩破坏试验 |
现已知岩爆发生的一个必要条件:主应力差(σ1-σ3)的值较大〔4〕; 换句话说, 没有主应力差或主应力差较小时, 岩石是不会发生岩爆的。也就是说σ1-σ3愈大, 发生岩爆的概率就愈大, 两者有着成正比的关系。特别是σ1远远大于σ3(即σ1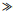
 |
| 图 2 由两种不同构件组成的力学模型 |
2 岩石发生突然失稳破坏(即岩爆)的新观点的提出与论证
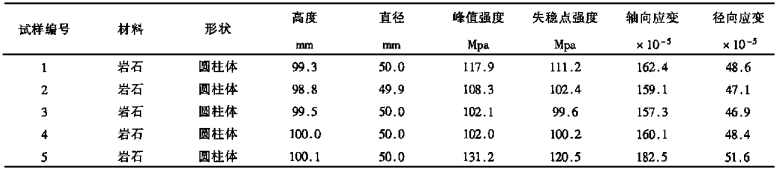
笔者在中南工业大学测试中心使用Instron1342电液伺服控制试验机所做的一组试验中, 所记录的有关数据见表 2, 观察到试样突然破坏点的情况见图 3。
| 表 2 试件材料及其破坏后的有关数据 |
 |
| 点击放大 |
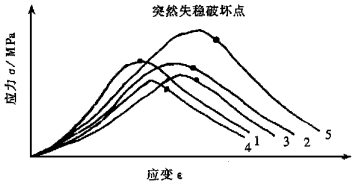 |
| 图 3 不同岩样在单向压缩破坏下发生的突然失稳的情况 |
通过试验观察发现, 在岩石的压缩破坏试验过程中, 从岩爆的角度来说, 岩石的突然失稳破坏(简称突然破坏, 解释为岩石以数块的方式即将分离母体的时刻, 即岩爆发生的时刻)并非发生在峰值处, 而是发生在过峰值后的某一点。而峰值只是试样的破损点, 即岩石在此并非发生突然破坏。为进一步证实岩石突然失稳的情况, 还对不同种类或同一种类岩样进行了不同的试验, 尽管所观察得到的突然破坏点的位置不一, 有的靠近峰值, 有的稍远离峰值, 但都是过峰值之后的某一点。上述试验就是如此。这非偶然, 为此从理论上给予论证。
根据图 2, 以岩样下端为固定的参考点, 岩样上端坐标计为x, 当岩样不受力时弹簧另一端的坐标计为xO; 当弹簧一端受压时, 设坐标为xO′, 则其产生的位移设为uO; 此时岩样上端面的坐标将变成x′, 同时产生的位移设为u(位移的正负方向规定如图 2所示)。
弹簧施加于岩样的力为F, 根据虎克定律, F与弹簧的相对压缩量(uO-u)成正比, 即:
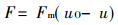
|
(1) |
从上式可以看出, 如果一个弹簧很硬, 其刚度就愈大, 也就是说, 把弹簧压缩单位长度所需的力就大; 反之, 如果弹簧长度发生单位长度的变化, 其上的力变化也大。如果一个弹簧很软, 其刚度就小。不难证明, 有如下两种特殊情况。
一种是常力加载相当于刚度K=0的情况。因为K=F/(uo-u)=-dF/du, 现dF=0, 故K=0。
另一种零位移加载, 则du=0, 相当于:K=∞的情况。
一般而言, 弹性加载相当于K为一个不为0的有限值的情况。现进一步把F=Km(uo-u)改写成:
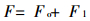
|
(2) |
式中:Fo=Kmuo, 与岩样位移u无关的初始力;
F1=-Kmu, 与岩样位移u有关的初始力。
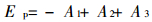
|
(3) |
式中:A1—弹簧做的功, A1=∫Fdu=
∫(Fo +F1)du=Fou-1/2Kmu2;
A2—岩石内部贮存的弹性应变能;
A3—岩石在压缩过程中所耗的能量。
因A2+A3≈∫f(u)du(即全应力应变曲线与坐标轴所围成的面积), 所以系统的总势能又可写成:
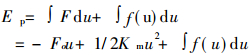
|
(4) |
为了使问题明确化, 有必要在此对稳定和失稳做简要的说明。假定在应力作用下, 岩石发生变形, 达到了某一平衡状态, 若给这个状态一个小的扰动, 看它是否具有回归到原来状态的倾向, 如果有这种倾向, 则称这个状态是稳定的; 如果它将进一步偏离这个状态, 则称此状态是不稳定的, 或者说岩石发生了失稳破坏; 如果它既不回归原状态也不进一步偏离, 则称随遇平衡, 实际上随遇平衡是一个临界状态。
为了判别平衡状态的稳定性质, 根据断裂力学中的系统平衡的条件(即失稳的必要条件)可得:
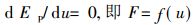
|
(5) |
而系统的失稳条件是由Ep的二阶导数给出, 即必须满足:
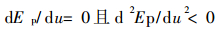
|
(6) |
把(4)式代入(6)式可得:
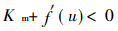
|
(7) |
由于Km永远为正值(它代表弹簧的刚度), 要使得上述不等式成立, 必须满足:
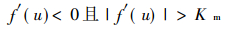
|
(8) |
从全应力应变曲线来看, f′(u) < 0只有过峰值后才能成立, 如图 4所示。
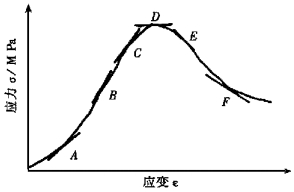 |
| 图 4 应力应变曲线上各点切线斜率的对比 |
这样从理论上证明了试样的突然失稳破坏只有过峰值后才能发生, 这与在试验过程中所观察到的结果是一致的。
3 结语根据以上分析研究可以看出, 矿山岩爆一般发生在矿柱当中, 而且具有普遍性。通过建立其力学模型, 从理论和实践的角度都证明了岩石的突然破坏(即岩爆)应发生在全应力应变曲线过峰值后的某一处, 而该峰值只是岩石的破坏点, 过峰值时并未发生突然破坏, 这一点非常重要; 并指出在研究岩爆时, 既要考虑岩石的破坏前区, 又不可忽视岩石的破坏后区(指的是全应力应变曲线过峰值的后半部分); 同时还反映了岩爆发生的时刻。为今后进一步研究矿山岩爆和建立预测预报方法都有一定的参考价值。
| [1] |
王文星.
岩体力学[M]. 长沙: 中南工业大学出版社, 1997: 2-3.
|
| [2] |
陈宗基. 岩爆的工程实录、理论与控制[J].
岩石力学与工程学报, 1987, 6(1): 1–3.
|
| [3] |
唐宝庆, 曹平. 引起岩爆因素的探讨[J].
江西有色金属, 1995, 9(4): 4–8.
|
| [4] |
周维垣.
高等岩石力学[M]. 北京: 水利电力出版社, 1993: 422-430.
|
 2000, Vol. 14
2000, Vol. 14
