| 裂隙岩体的渗流特性研究 |
在许多岩土工程、矿山工程及地球物理勘探过程中, 岩体的渗透率起到十分重要的作用, 但在理论上尚未引起足够的重视, 通常将岩体渗流处理为砂土一样的多孔介质, 用连续介质力学方法求解。参考文献〔1~2〕介绍了国外曾讨论过一些岩体中的渗流特性。这里简单说明一下岩体和土体中流动特性的差别:在土体中孔隙一般是连通的, 而岩体中有许多孤立裂隙, 它们对流体的运动不起作用; 土体中的孔隙一般是体积压实各向同性的, 其体积在压力作用下没有明显的变化, 而岩体受压后裂隙闭合, 体积减小, 从而影响到流体在裂隙中的流动; 岩体中的裂隙宏观上趋于定向排列, 而土体中的孔隙呈各向同性分布。故岩体中的渗透率为张量, 具有很大的方向性。
综上所述, 分析流体在岩体中的渗流特性时应考虑以下因素:每一裂隙的平均流量; 单位体积内的裂隙数; 以及裂隙连通的程度。第一个因素系考虑每一裂隙的流量问题, 采用Poiseuille方程的层状粘性流动解, 第二个因素引用Dienes〔3〕的结论, 第三个因素由渗流理论分析。由此解释岩体在压力作用下的优先成裂机理。
1 岩体渗流特性分析地质材料的渗透性可通过孔隙的连通以及裂隙的层面流动来分析。笔者仅考虑后一种因素, 将岩体考虑为由许多薄层(即层理)组成, 每一层的流动压力梯度按Poiseuille方程计算:
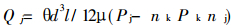
|
(1) |
式中:Qj—j方向的流量分量;
l—裂隙长度;
d—裂隙最大厚度;
μ—流体粘性系数;
nk—连通面的法向分量;
nj—裂隙面的法向分量;
Pj—裂隙面压力梯度;
Pk—连通面的压力梯度;
θ—考虑裂隙形状偏离裂隙主向的影响系数, 其估计值是1/2。
上式右边括号内的项是裂隙面上的压力梯度分量。由于裂隙端部效应及裂隙面粗糙度的影响, θ的实际值较估计值(1/2)小。
令δNsα代表单位体积内裂隙连通的数密度, 连通面为S, α为第α组裂隙的方向, 令ñk代表S平面的法向方向。于是, 通过S面的流量为:

|
(2) |
式中字母头上符号“ ~ ”表示张量。
定义渗透率张量为:

|
(3) |
式中: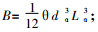

|
其中:δjk—为Kronecker张量, j=k时为1, 否则为零。
单位体积的裂隙数密度为:

|
(4) |
式中:δΩ—球面角元素;
δl—裂隙线长度元素。
如考虑裂隙组是可积的特殊情况, 其和为:

|
(5) |
在Ω上的积分用单位球体的上半域代替, 并引入2π的球面角。Dienes〔3〕表明N与2π内每单位体积裂隙分布Nc(V、Ω)的关系为:

|
(6) |
式中:γs—S面与裂隙组方向α间的夹角, 其值可由下式求得:cosγs=nk·nk。
综合上述有关结论, 以裂隙形态比A(Ω)=h/l为参数写出张开裂隙的宽度为:

|
(7) |
即有:

|
(8) |
其中:

|
(9) |

|
(10) |
式中:V—为裂隙体积;
N0—代表单位体积内裂隙连通的数量。
式(9)表明G(Ω)为V的五阶矩。后面将在Liouville方程的基础上导出N的表达式。用有限差分法可计算式(8)的积分方程。如果裂隙各向同性分布, 方程(8)的解析结果为:

|
(11) |
此时3个渗流主向的渗透率相等。同时还可以看出, 所有的裂隙有相同的形态参数比A, 此结果对最简单的应力场是成立的, 但不具有普遍性。如将裂隙分布考虑为各向同性部分与层状部分之和, 则G (Ω)可表达为:

|
(12) |
式中:δ—Diracδ函数。
由此得到渗透率是两部分之和:

|
(13) |
式中: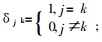

|
文献〔3~4〕的研究资料表明, 硬岩及其他材料中裂隙大小的分布服从指数函数。随着裂隙的扩展与连通, 此分布规律亦将发生变化。对于简单情况, 假设裂隙既可呈活性状态—即不稳定时具有扩展的能力, 又可呈非活性状态—即稳定时停止扩展, 此时裂隙的连通数为σ, 以σ=4为例进行分析。当不稳定时(呈活性状态), 假设裂隙以速率Ċ增长, 为分析方便假设Ċ为常量, Dienes〔5〕表明裂隙分布按Liouville方程发展:

|
(14) |
式中:L、M—分别表示活性裂隙与非活性裂隙的分布。
对于稀疏分布的裂隙, 非活性部分可表达为:

|
(15) |
式中:K—为非活性裂隙生成速率。
假设不同方向的裂隙组彼此独立地增长, 以及K由初始分布确定。由此, 对于各向同性与成层裂隙的综合分布, 得到K的估计值为:

|
(16) |
式中:Lio—每2π内各向同性裂隙的初始密度;
L bo—层状裂隙的初始密度。
假定裂隙的初始分布为指数函数, 求解方程(14)可得到活性裂隙的分布为:

|
(17) |
式中: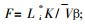

|
利用此分布函数, 由式(9)计算G(Ω), 最后得到:

|
(18) |
如果由各向同性裂隙与成层裂隙之和来表达裂隙的分布, 则与式(12)一样, G∞将也是各向同性与成层裂隙两部分之和。如果裂隙分布中以成层裂隙为主(如板页岩), 于是从式(16)中就可以得到非活性裂隙生成的平均速率为:

|
(19) |
由于成层裂隙相互平行而彼此无连通, 裂隙连通的速率由各向同性裂隙控制, 则有:

|
(20) |
于是对各向同性裂隙与成层裂隙两种情况有:

|
(21) |
利用随机理论建立渗流模型的基本思想是:如果裂隙是稀疏连通的, 那么无穷远处裂隙连通的概率为零; 如裂隙连通数量超过一极限值, 那么就存在远处裂隙通道, 裂隙呈孤立状态的概率不再是零。
令q代表两个(组)各向同性均匀裂隙互不连通的概率, Q表示裂隙1通过其相邻裂隙2的连通概率, 设A为它们之间的通道, 如图 1所示。由于裂隙1与2可能不连通, 或者如果裂隙1与2连通, 但从2的σ-1条通道是有限的, 故由裂隙1出发的通道也有限。假设σ=4, 用代数式表达为:

|
(22) |
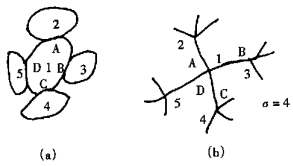 |
| 图 1 裂隙连通情况及其渗流分析图 |
如图 1中所示, 在分析中假设裂隙1间连通数目为4, 此时裂隙1处于稳定状态, 整个体系为非活性裂隙。选择σ=4仅为数学上分析方便, 为其他值时可按同样方法分析。变量Q满足关系0≤Q≤1, 故得到方程(22)的限制条件为:

|
(23) |
如果相互未连通的概率q > 2/3, 那么由方程(22)有Q>1, 表示裂隙1与其他裂隙的通道是无限的, 第二个根就无意义。在计算裂隙岩体的渗透率时, 要求计算裂隙未被孤立的比率P。当一个裂隙只与另一个裂隙或不与其他裂隙连通时, 则认为它是孤立的; 如果它与其他两个或两个以上裂隙相连通, 那么它就不是孤立的。将其简单地表达为:

|
(24) |
现讨论各向异性的裂隙体系, 仍将渗流模型考虑为有两组裂隙的情况, 一组是各向同性裂隙, 另一组位于成层平面上, 这里仅归纳分析结果。通过前面对各向同性裂隙的一般性讨论, 可以得到各向同性裂隙连通的比例由函数fi=f(R)(i=1.2)给出, 式中R是下面方程的根:

|
(25) |
式中的下标1、2分别表示各向同性裂隙与成层裂隙。
于是qij就是一个i型裂隙与一个j型裂隙(i、j=1、2)未连通的概率, 且Pij=1 -qij。类似地, Qij表示从一个i型裂隙出发连通一个j型裂隙的有限概率。参数ri表示贯穿i型裂隙的线密度(裂隙数目)。非孤立成层裂隙的比例fb由函数f(Q21)给出, f函数为式(24), Q21为:

|
(26) |
在数值计算中, fi及fb分别乘以式(12)中的Gi和Gb, 最后就可得到裂隙岩体的渗透率张量。与各向同性裂隙系统一样, 对各向异性裂隙系统也存在一个极限概率值, 由方程(25)在R=1时有一重根, 由这一条件可以得到如下准则:

|
(27) |
式中:r=3P11-1;
S=9P12P21-1。
此准则对任意状态(孤立或连通)的裂隙都适用, 通过图 2的极值线说明了这一准则。在临界线圈闭合的渗流区域内, 通过一裂隙系统的渗流是可能的, 否则因裂隙连通的数目太少不足以提供连续的通道。流动迹线表明了参数r、s随裂隙不稳定时间的变化情况, 如果成层裂隙的数目趋于零, 于是有r2=0, 那么这时的极值条件就与前一部分所讨论的各向同性裂隙系统的极值条件一致。
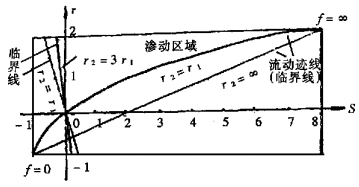 |
| 图 2 渗流临界条件说明图 |
4 结语
本文将裂隙连通的随机理论与流体通过裂隙的水力学理论相结合, 建立起裂隙岩体的渗流模型。将岩体渗透性分解为各向同性部分和层面渗流部分(13), 导出了裂隙扩展方程(21)。根据裂隙的形态, 得到相互连通的概率方程(24)。最后, 对各向异性裂隙岩体导出了渗透性的存在准则(27), 图 2绘出了岩体裂隙分布与渗流条件的关系。这些结论有助于分析裂隙岩体的渗流能力, 对实际工程亦有参考价值。
| [1] |
Withers poon P A, et al.New approaches to problems of fluid flow in fra cture rock mass〔A〕. 22 nd U S s ymposium on rock mechanics 〔C]. M.I.T.1981.34-39.
|
| [2] |
Bear J Z. 多孔介质流体动力学〔M〕. 李竟生等译. 北京: 建筑工业出版社, 1983. 104-113.
|
| [3] |
Dienes J K.On the inference of crack statistics from observations on an out cropping〔A〕. 20 th symposium on rock mechanics〔C〕. Austin. 1979.137-143.
|
| [4] |
曹敦履. 裂隙岩体渗流的Monte-Carlo模拟[J].
长江科学院院报, 1989(3): 55–61.
|
| [5] |
Dienes J K.A statistical theory of fragmentation〔A〕. 23 rd U S symposium on rock mechanics〔C〕. State line.NY.1983.68-73.
|
 2000, Vol. 14
2000, Vol. 14
