| 皮带给矿机减速器的模糊优化设计 |
通常矿山的皮带给矿机以及一般物料输送机都有减速器。如何提高减速器的传动效率,在保证承载能力条件下,使减速器质量最轻,这一直是减速器设计中的一个重要问题。现用模糊优化的设计方法,改变原来不够完善的常规数学模型,考虑在变载荷作用下全部约束条件的模糊性和影响齿轮传动各种因素的模糊性,建立了它的模糊优化数学模型,进行了模糊优化设计,取得了好的设计效果。
1 数学模型的建立 1.1 原始条件已知皮带给矿机减速器,采用单级直齿圆柱齿轮传动,名义功率P=20kW,小齿轮转速n1= 1000r/min;传动比i=3,载荷变化规律见图 1。单班制,预期使用寿命10年,每年300个工作日,在使用期限内,工作时间占20%。动力机为电动机,工作时有中等振动、传动不逆转、齿轮对称布置。传动尺寸无严格限制,大批量生产,齿面允许少量点蚀。要求确定减速器的结构参数,以在保证承载能力条件下,减速器的质量最轻。大小齿轮选用45#钢,小齿轮调质处理,平均硬度260HB;大齿轮正火处理,平均硬度200HB。主、从动轴均采用45#钢调质。
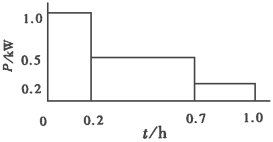 |
| 图 1 载荷变化规律 |
1.2 确定设计变量
根据设计要求,在满足强度的条件下,使减速器的质量最轻。而影响减速器质量的主要参数有:齿宽b、小齿轮齿数z1、模数m、轴承跨距l、主动轴直径ds1、从动轴直径ds2、传动比i等7个参数[1]。其中i为设计常量,由已知条件给定。所以可取设计变量为:
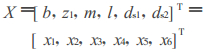
|
(1) |
减速器的质量有两部分组成,其一为内部齿轮、轴的质量;其二为箱体的质量,它们都取决于齿轮和轴的尺寸大小。因此,取齿轮和轴的体积最小为目标函数。
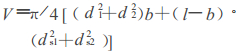
|
(2) |
将d1=mz1, d2=mz1i代入式(2),整理得目标函数:
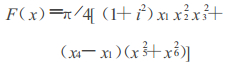
|
(3) |
(1) 齿面接触应力约束:
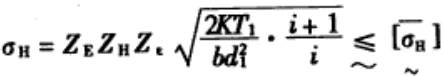
|
(4) |
式中:K—载荷系数;
ZE—弹性系数;
ZH—节点区域系数;
Zε—重合度系数;
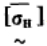
(2)齿根弯曲应力约束:
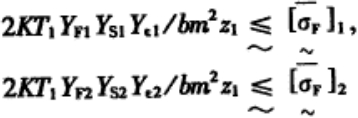
|
(5) |
式中:YF—齿轮系数;
YS—应力修正系数;
Yε—重合度系数;
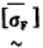
(3) 主动轴、从动轴的弯曲应力约束:
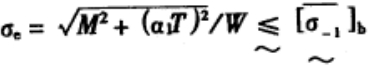
|
(6) |
式中:M—轴的危险剖面所受弯矩;
α1—扭矩校正系数;
W—抗弯剖面系数;
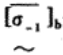
(4) 主动轴刚度约束:
式中:Fn—轮齿齿面上作用的法向压力;
E—齿轮材料的弹性模量;
J—惯性矩;
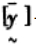
(5) 齿宽系数ψd约束:
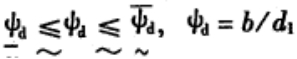
|
(8) |
(6) 设计变量的上、下限约束:

|
(9) |
以上各约束中符号“~”表示具有模糊性。综上所述,该问题的模糊优化设计,设计变量和目标函数都是确定的,只有约束条件是模糊的,是一个具有普通模糊约束的非对称模糊优化模型。
2 模糊约束向非模糊约束的转化模糊约束一般不能直接上机计算,必须借助于隶属函数,将模糊约束转化为非模糊约束。对于一般的工程问题,隶属函数大多数采用线性函数。
当模糊约束为0≤g≤ 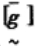
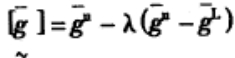
|
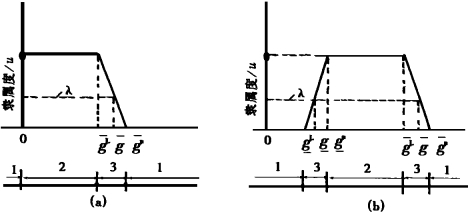 |
| 1•不许用区;2•许用区;3•过渡区 图 2 隶属函数图 |
当模糊约束为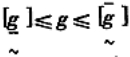
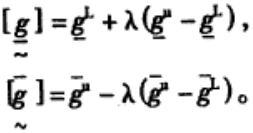
|
式中: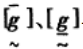
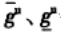
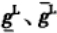
λ—截集水平,在[0, 1]区间的下界。
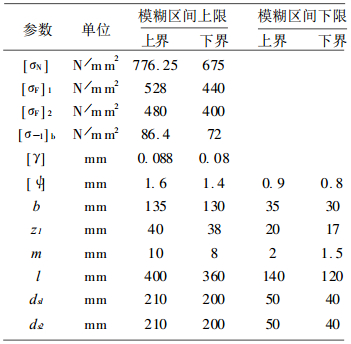
建立模糊约束的隶属函数时,必须确定模糊过渡区间的上界u、u和下界L、L,否则其隶属函数将是不定的,不能具体计算。文献[2]介绍了一种常用的确定过渡区间上下界的方法—扩增系数法。该法充分考虑了长期以来普通设计所积累的经验,在设计规范给出的许用值的基础上,通过引用一扩增系数β来确定上下界。一般β=1.05~1.30。模糊约束过渡区间的上下界见表 1。
| 表 1 模糊约束过渡区间上下界 |
 |
| 点击放大 |
由于本例所受载荷为变载荷,故[σH]、[σF]1、[σF]2、[σ-1]b的下界值需根据疲劳积累假说确定,见文献[3]。
确定了模糊约束的上下界之后,就可将模糊优化模型转化为截集水平为λ的非模糊优化模型。
模糊约束向非模糊约束转化:

|
(10) |
将上式代入(4)~(9)式,取不同的λ值,就得到不同截集水平下的优化方案。λ越小越经济,λ越大越安全可靠。λ取1,模糊优化即转化为普通优化。如果问题的规模较大,这种方法的工作量十分惊人。为了使方案既安全可靠又经济,需确定一个最优截集水平λ*。但λ*值受多种模糊因素的影响,因此考虑了设计水平、制造水平、材料好坏、使用程度、重要程度和维护费用等模糊因素,采用二级模糊综合评判方法[2],经过建立因素集、建立备择集、一级模糊综合评判、二级模糊综合评判,按加权平均法求得λ*=0.48。
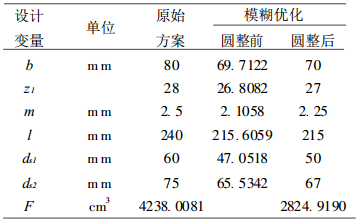
3 优化结果针对上述数学模型,优化方法可采用直接寻优的复合形法、正多面体法或间接寻优的内外点惩罚函数法求解。现采用复合形法,对于模数和齿数,计算时按连续变量处理,求出优化结果后进行圆整,并使模数符合荐用系列,齿数取整。轴径按GB2822-81圆整。取λ=λ*进行模糊优化,以原设计方案为初始点:x[0]=[80, 28, 2.5, 240, 60, 75]T,其模糊优化结果见表 2。
| 表 2 模糊优化结果 |
 |
| 点击放大 |
4 结语
模糊优化设计考虑了设计中各变量的模糊性,因此文中的优化模型和优化方案比常规优化更接近客观实际。计算结果表明,模糊优化与原设计方案相比,质量减少了33.34%。在大批量生产中可望获得显著的经济效益。
| [1] |
曾昭华, 傅祥志.
优化设计[M]. 北京: 机械工业出版社, 1992: 307-313.
|
| [2] |
王彩华, 宋连天.
模糊论方法学[M]. 北京: 中国建筑工业出版社, 1988: 175-298.
|
| [3] |
邱宣怀主编. 机械设计. 北京: 高等教育出版社, 1992. 37~195
|
 1999, Vol. 13
1999, Vol. 13
