| 空间四杆机构的解析综合及程序设计 |
与平面机构相比, 空间机构有不少特点, 如结构紧凑、运行多样、工作可靠等。需要用复杂平面机构才能实现的运动以及用平面机构根本无法实现的运动, 往往可用空间机构来完成。但是, 由于空间机构的分析设计比较困难, 很难应用直观试凑法进行设计。至于几何作图法, 又局限于解决比较简单的设计问题。因此, 发展空间机构的解析法, 有着特别重要的意义。近20年来, 由于电子计算机的应用, 空间机构的解析法研究已成为世界各国机构学专家们极感兴趣的课题, 涌现出多种研究方法, 如矢量法、方向余弦矩阵法、二元数法、四元数法、张量法、旋量法等。现根据方向余弦矩阵法所建立的空间四杆机构输出输入位移方程式, 结合不同的预选参数, 建立按主从动件3组对应位置、按从动件两极限位置以及按给定函数关系等机构综合的数学模型, 并用同一个计算机程序解决多种命题。
1 输出输入位移方程式 1.1 RSSR空间四杆机构含有首末两个转动副和两个中间球面副, 如图 1所示。θ1为输入角, θ3为输出角, 输出输入位移方程式是指θ3与θ1的变化关系。用矩阵法研究机构时, 为了把机构的运动问题抽象为坐标的变换问题, 在需要分析运动的构件上固结有相应的直角坐标系, 图 1中, 与机架4、主动件1及从动件3分别固结坐标系a-X4(Y4)Z4, A-X1(Y1)Z1及D-X3(Y3)Z3, 而连杆2上则没有安置坐标系。
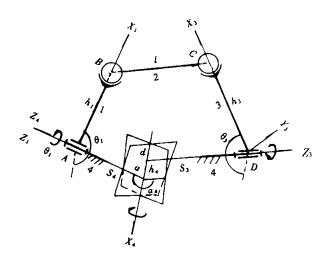 |
| 图 1 RSSR空间四杆机构 |
为了直接求θ3与θ1的关系式, 假想连杆2拆离。由于机构运动时, B、C两点间的距离始终保持定长, 即B、C两点的流动坐标要受到连杆l的约束。因此, 杆2拆离后, 机构运动时, 仍应保持下列几何等同关系式:
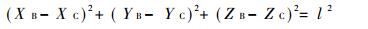
|
由文献[1]用不共原点的坐标变换法可写出B、C两点在参考坐标系a-X4(Y4)Z4中的流动坐标, 代入上式并展开整理, 可得RSSR机构的输出输入位移方程式[1]如下:
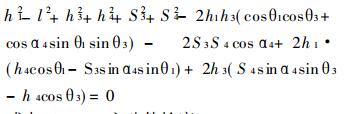
|
(1) |
式中: h1 —主动件长度;
l—连杆长度;
h3 —从动件长度;
h4 —机架长度;
S3 —从动件轴向位置距离;
S4 —主动件轴向位置距离;
α4 —机架角度。
1.2 RSSP空间四杆机构将图 1中构件3与机架4组成的转动副换成移动副, 并令h3 =0, 便得到图 2所示的RSSP空间四杆机构。此时, 由于X3轴可取与X4轴平行, 所以θ3 =0°, 但S3成为运动变量, 表示滑块3的输出位移。
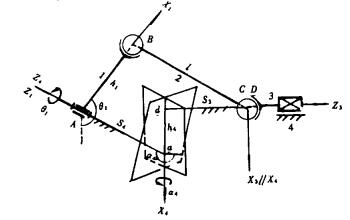 |
| 图 2 RSSP空间四杆机构 |
空间RSSP机构的输出输入位移方程式可由式(1)推导出。将h3 =0和θ3 =0代入式(1)可得:
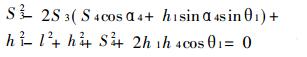
|
(2) |
RSSR机构可供设计的参数有7个, 即α4、h1、h3、h4、S3、S4、l。因此, 按主、从动件三组对应位置进行机构综合时, 应预先选定4个参数, 再按设计要求计算其余3个参数, 随着预选参数的不同, 设计方程式的形式也不相同。以θ1 =φi及θ3 =ψi代入式(1), 分以下4种情况讨论。
(1) 预定α4 =90°、h1、h4、S3, 求h3、S4、l :
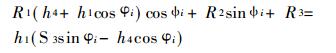
|
(3) |
式中: R1 =-h3; R2 =h3S4;
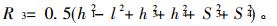
|
(2)预定α4 =90°、h1、h4、S4, 求h3、S3、l :
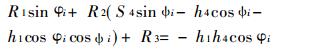
|
(4) |
式中: R1 =-h1S3; R2 =h3;
R3同(3)式R3。
(3) 预定α4=90°、h1、h3、S3, 求h4、S4、l :
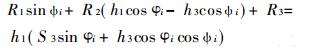
|
(5) |
式中: R1 =h3 S4; R2 =h4;
R3同(3)式R3。
(4) 预定α4=90°、h1、h3、S4, 求h4、S3、l :
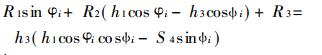
|
(6) |
式中: R1 =-h1S3; R2 =h4;
R3同(3)式R3。
将主、从件的三组对应角度φi、ψi (i =1, 2, 3)分别代入式(3)、(4)、(5)、(6)解出R1、R2、R3后, 再分别求出待设计的3个参数。
2.2 RSSP空间四杆机构RSSP机构可供设计的参数有5个, 即α4、l、h1、h4、S4。如果预定α4 =90°, 并用φi代替θ1和Si代替S3, 则(2)式可写成如下的设计方程式:
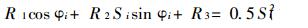
|
(7) |
式中: R1 =-h1h4; R2 =h1;
R3 =0.5(l2-h12-h42-S42)。
预选参数l, 将主、从动件三组对应位置φi、Si(i=1, 2, 3)分别代入上式, 解出R1、R2、R3后, 再求出未知参数h1、h4、S4。
3 按从动件两极限位置的机构综合 3.1 RSSR空间四杆机构当从动件3处于极限位置时, 其瞬时角速度为零。将式(1)对时间求一阶导数, 并令dθ1/dt =ω1, dθ3/dt =ω3, 经整理得:
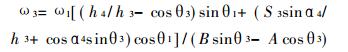
|
式中: A =cos α4sin θ1-S4sin α4/h1;
B =h4/h1 +cosθ1。
令ω3 =0, 可得从动件3处于极限位置时, 输入角与输出角之间的关系式为:
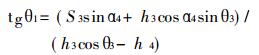
|
(8) |
由上式可知, 只要预先选定S3、h3、h4及α4 =90°4个参数的值, 就可由θ3求出θ1。这样RSSR机构可供设计的7个参数中还剩h1、l及S4 3个参数。将θ1 = φi, θ3 =ψ i(i =1, 2)代入式(1)可得2个线性方程, 而未知数却有3个。因此可在h1、l及S4中再预选一个参数, 如S4, 得出设计方程式为:
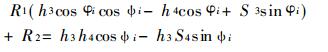
|
(9) |
式中: R1 =-h1; R2同(3)式R3。
3.2 RSSP空间四杆机构将式(2)对时间t求一阶导数, 并令dθ1/dt =ω1, d S3/d t=V3, 经整理得:
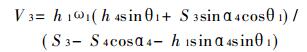
|
令V3 =0, 可得滑块处于极限位置时的输入角与输出位移之间的关系式为:
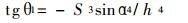
|
(10) |
由上式知, 预定h4, α4, 可由S3求出θ1。将θ1=φi, S3 =Si(i =1, 2)代入式(2)可得两个线性方程式, 再预选S4, 可求出h1和l两个参数。设计方程式为:
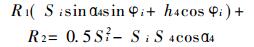
|
(11) |
式中: R1 =h1; R2同(7)式R3。
4 按给定函数关系的机构综合按给定函数关系设计空间四杆机构, 在方法上与设计平面机构相似。对于RSSP机构, 可预先选定α4, 以θ1 = φi, S3=Si代入式(2)并整理得:
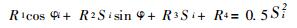
|
(12) |
式中: R1=-h1 h4; R2 =h1sin α4;
R3=S4cosα4; R4同(7)式R3。
式(12)中有4个未知量R1、R2、R3、R4, 可根据戚贝谢夫的精确点布置法, 计算出4个精确点来实现函数关系。将φi, Si(i=1, 2, 3, 4)代入式(12), 解出R1、R2、R3、R4后, 利用下式求出以下设计参数:
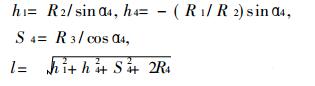
|
(13) |
对于RSS R、RSSP空间四杆机构, 以上讨论了8种综合方法。由各种方法的设计方程式可看出, 它们具有相同的方程形式, 且都为线性方程, 可以通过高斯列主元消元法求解。为了解决这8种命题, 采用C语言进行编程, 将每种综合方法编写成单独的函数[2], 函数与函数间互不影响, 以便于修改及扩充。限于篇幅, 下面仅给出RSSR机构的一个计算实例。
例:已知主动杆的三个位置转角为φ1= 47°, φ2=75°, φ3=108°; 从动杆的相应转角为ψ1= 307°, ψ2=279°, ψ3 =233°。计算结果见表 1。
| 表 1 RSSR机构按主、从动件三位置综合的计算结果 |
 |
| 点击放大 |
6 结语
(1) 数学模型格式统一, 所得方程均为线性方程, 可避免求解非线性方程组。
(2) 数学模型推导过程及程序编写方法同样适合于其他空间机构。这种方法概念明确、清晰, 易为设计者掌握和便于灵活应用。
| [1] |
祝毓琥主编. 机械原理(上). 北京: 高等教育出版社, 1986. 124~137
|
| [2] |
徐金梧, 刘冶铜, 倪伟敏编译. T urbo C使用大全(第一册). 北京: 北京科海培训中心, 1990. 51~73
|
 1998, Vol. 12
1998, Vol. 12
