| HD-2T4M回转悬臂吊车设计 |
有些厂矿在检修或抢修一些较大设备时, 受检修现场条件的限制, 无法使用起重设施, 通常是靠人工或手拉葫芦起吊检修设备, 劳动强度大。为此, 设计制造了一种通用性强、投资小、轻便灵活的HD-2T4M回转悬臂吊车, 经现场使用, 效果良好, 深受用户好评。
1.1 设计要求悬臂吊车的工作负荷P作用于旋臂上, 力矩M=P×l, l为负荷半径。设计要求P≤2t, l≤4m, 在结构性能上力求简单、轻便、灵活和实用。
1.2 选型设计(1) 选用2t电动链环葫芦作该吊车的动力(重约65kg); 电葫芦的水平运动可选用WA2型2t手拉单轨行车(重约24kg)。
(2) 悬臂的回转宜采用人力拖动, 为增加其回转的平稳性, 转动轴承宜采用滑动轴承。
1.3 结构设计根据设计要求和选型设计, 该吊车的悬臂架采用行架结构, 用型钢焊接而成, 其结构简图如图 1所示。
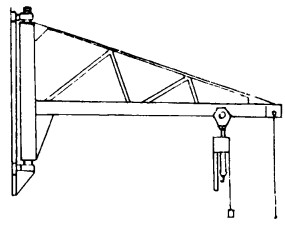 |
| 图 1 悬臂架结构示意图 |
2 悬臂架受力分析与计算
从悬臂架结构示意图可知, 各杆件截面尺寸与其长度相比要小得多, 故可简化成一根通过其截面形心的等直杆来处理; 角铁构件截面尺寸也比其长度小得多, 可视为根本不能承受弯矩作用, 将其简化成两端铰接的拉压杆来处理; 工字钢构件需承受弯矩作用, 不能视为简单的拉压杆来处理, 只能简化成一根通过其形心的等直梁来处理, 这是一根超静定的等直梁。经以上简化就得到了悬臂架的力学模型图, 如图 2所示。
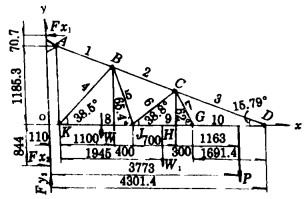 |
| 图 2 悬臂架结构简图 |
2.1 外力
以整个悬臂架为研究对象, 悬臂架受5个外力的作用; P是外载荷(20472N), 包括手拉单轨行车和电动葫芦的自重; W是整个悬臂架的自重(4165N); Fx1、Fx2、Fy2都是支座反力。
悬臂架上除关于oy轴对称的构件外, 其余构件的自重均对oz之轴产生顺时针方向的力矩(x、y、z组成正交坐标系)。设这些构件的自重为W1, 查表可求得W1=1784N, 而W1距oy轴的距离约为2055mm。对整体悬臂架, 由平面任意力系平衡方程可求得:
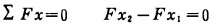
|
(1) |
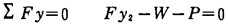
|
(2) |
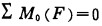
|
(3) |
即
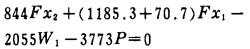
|
解得:
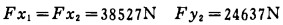
|
在计算各杆的内力时, 因杆的自重与外载荷相比要小得多, 一般可忽略不计。但对危险性较大的拉杆1来说, 为安全起见, 可将W1视为一外载荷并将其加在工字梁上的H点。据此, 做出工字梁的相当系统图和各跨梁的载荷弯矩图[1], 见图 3和图 4所示。
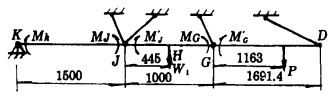 |
| 图 3 工字梁相当系统图 |
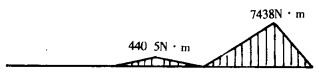 |
| 图 4 各跨简支梁载荷弯矩图 |
由于梁左边是固定端, 中间有两个支座, 因此可写出3个弯矩方程式。
(1) 相当系统在铰接K处应满足的变形条件是QK=0, 其三弯矩方程式为:
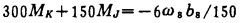
|
(4) |
式中:ω8————简支梁8的截荷弯矩图面积;
b8————形心距右支座的距离。
因ω8=0, 故
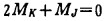
|
(5) |
(2) 相当系统在铰接J处应满足的变形条件是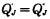
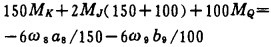
|
(6) |
式中:a8——简支梁8上载荷弯矩图面积形心到左支座的距离;
ω9——简支梁9上载荷弯矩图面积, 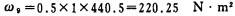
b9——形心到右支座的距离,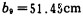
将已知量代入(6)式并简化得:
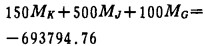
|
(7) |
(3) 相当系统在铰接G处应满足的变形条件是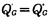
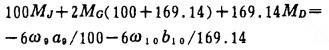
|
(8) |
式中:MD=0;
a9——简支梁9上截荷弯矩图面积形心到左支座的距离, a9=48.55cm;
ω10——简支梁10上截荷弯矩图面积, 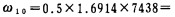
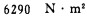
b10——形心到右支座的距离, 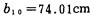
将已知量代扩(8)式并简化得:
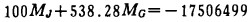
|
(9) |
联解(5)、(7)、(9)三式得支座K、J、G处截面上的弯矩分别为:

|
负值说明与图 3中的假设方向相反。
根据MK、MJ、MG的大小和方向绘出各跨梁的弯矩图(图 5), 然后与相应跨梁的截荷弯矩图(图 4)叠加, 就得到相当系统的弯矩图(图 6), 也就是连续梁的弯矩图。
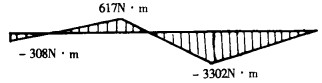 |
| 图 5 各跨梁弯矩图 |
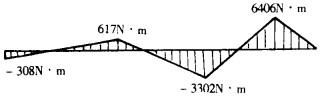 |
| 图 6 相当系统弯矩图 |
要绘出剪力图, 应先计算出相当系统中每一跨梁的两个支座在y方向上的支反力。对于第8段梁可写出两个平衡方程式:
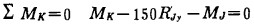
|
(10) |
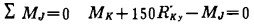
|
(11) |
式中:R''Ky——左支座K对简支梁8在y方向上的支反力;
R'Jy——右支座J对简支梁8在y方向上的支承力。
解得:
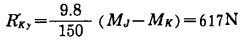
|
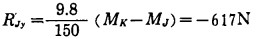
|
对于第9节梁, 两个力矩平衡方程式为:
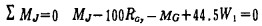
|
(12) |
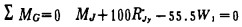
|
(13) |
式中:R''Jy——左支座在y方向上的支反力;
R'Gy——右支座在y方向上的支反力。
解得:
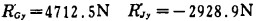
|
对于第10节梁两个力矩平衡方程式为:
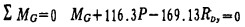
|
(14) |
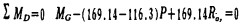
|
(15) |
式中:R''Gy——左支座在y方向上的支反力;
R'Gy——右支座在y方向上的支反力。
解得:
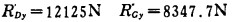
|
根据相当系统每一跨梁在y方向上的支反力绘出梁的剪力图, 如图 7所示。
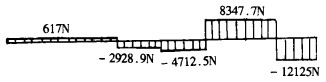 |
| 图 7 相当系统剪力图 |
由各跨梁的支反力可求出连续梁各支座处y方向上的支反力, 即:
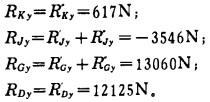
|
负值说明实际力的方向与y轴相反。
根据各支座处y方向上的支反力, 利用D、G节点求出杆3和杆7中的内力, 求得:
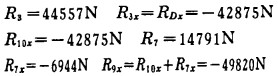
|
由节点C求出杆2和杆6的拉力为:
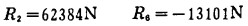
|
设杆5中的拉力为R5, 对于节点J, 支反力RJy是R5和R'6在y方向上的分力合成的, 分力以R5x、R5y和R'6x、R'6y表示, 求得:
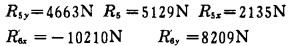
|
工字梁8中x轴方向上的压力为Rθ与R5x、R'6x之和, 即:
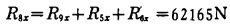
|
设杆1、4内的拉力为R1、R4, 断开杆1、2、4、5, 取出节点B, 绘出受力图, 见图 8所示。
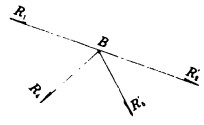 |
| 图 8 节点B受力图 |
根据平衡力系的平衡方程得:
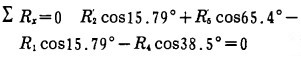
|
(16) |
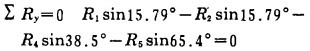
|
(17) |
其中:R'2=R2=62384N, R'6=R5= 5129N。联解(16)、(17)两式得:

|
设支座K左侧对简支梁8及杆4在x方向上的压应力为R'Kx, 则:
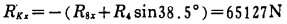
|
强度校核不是将臂架的每个构件和每条焊缝都进行强度计算, 而是将那些主要受力构件或焊缝以及危险性相对较大的受力构件和焊缝的强度进行校核。只要这些构件的强度达到要求, 说明整个悬臂架是安全的。
3.1 回转轴的强度计算从立柱结构看, 两端是最薄弱部位, 且直接受到支反力Fx的作用, Fx可视为沿两端轴颈均匀分布的线载荷, 因此只需验算立柱两端轴颈的强度。
(1) 线载荷: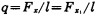
式中:l——端轴颈长度。
(2) 抗弯截面模量:
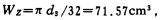
|
式中d——端轴颈直径。
(3) 截荷q对轴肩处产生的力矩:
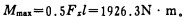
|
(4) 最大正应力:
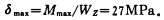
|
(5) 25#钢最大正极限应力[2]:
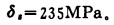
|
(6) 轴的安全系数: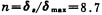
(7) 轴的名义挤压应力[1]:
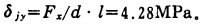
|
(8) 轴对弹性材料其最大抗挤压应力:
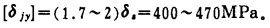
|
显然, δjy < < [δjy], 立柱满足强度条件。
3.2 拉杆1的强度计算最大拉力:R1=68516N;
截面积[2]:S=9.6cm2;
最大拉应力:δmax=R1/S=71.4MPa;
安全系数: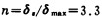
所以拉杆1满足强度条件。
4 结论从以上的设计计算和强度校核, 可以判定HD-2T4M回转悬臂吊车满足强度条件。该吊车已由某企业生产, 经用户反映, 吊车价格合理、方便使用, 是厂矿检修设备的理想起吊设备。
| [1] |
孙训方.
材料力学(下册)[M]. 北京: 人民教育出版社, 1978: 293-301.
|
| [2] |
东北工学院机械零件设计手册编写组.
机械零件设计手册[M]. 北京: 冶金工业出版社, 1979: 46-47.
|
 1998, Vol. 12
1998, Vol. 12
