| 溶剂萃取体系平衡计算过程中的数值分析 |
“漏斗法”稀土串级萃取分离实验即是单级萃取平衡与相转移的循环过程, 从实验中获得的信息往往只能是静态平衡体系各组份的平衡成分, 北大在串级萃取理论中采用计算机模拟稀土多组份恒定混合萃取比体系[1], 建立数学模型, 模拟萃取动态平衡过程, 克服了从分离实验中索取动态平衡过程中的有关参量所耗费的人力、物力和大量的分析化验费用。
计算机模拟“漏斗法”串级萃取实验是基于单级萃取达到平衡后, 被考查的各组份在两相的分配满足平衡关系式, 分离系数β即不同元素在两相分配比的比值是可以测定的。在分液漏斗中, 通过控制有机相的萃取量、各分离元素的总量及水相残留量, 建立模拟平衡关系式。模拟的关键是求解单级萃取平衡方程。方程的解法有很多[2], 但方程的解一定要符合槽体组份平衡的规律。
1 平衡体系设单级平衡体系有n种组份, 用m(i)、x(i)、y(i)(i=1, 2, …n)分别代表第i种组份在体系中的总量、水相平衡量、有机相平衡量, β(i/j)表示第i、j两种组份的分离系数(i < j, i组份为易萃组份), S为有机相萃取量, W为水相平衡金属量, 则平衡体系各组份满足:

|
(1) |

|
(2) |

|
(3) |
方程(1)、(2)、(3)构成非线性方程组。
2 求解过程及结果求解上述非线性方程组的解法有梯度法、拟牛顿法、改进牛顿法及Broyden法直接对方程组求解; 也可以先将方程组整理成某一未知数的一元高次方程, 然后用割线法、切线法、QR法、Bernoulli法、牛顿法等求解。采用P507为有机相, 经过皂化控制有机相萃取量S, 对含La、Ce、Pr、Nd 4组份的水相原料进行萃取分离, 建立数学平衡方程并采用迭代法求解平衡方程(组)。
2.1 一元高次方程求解由方程(1)(2)可得x(i)关于x(j)的方程:
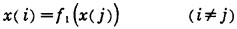
|
(4) |
将(2)、(4)式代入(3)式, 可得

|
(5) |
4种平衡成分n=4, 关于x(j)的四次方程为:

|
(6) |
β(Nd/Pr)=2,β(Pr/Ce)=4,β(Ce/La)=7为已知参量(该参数值为文章中设定值), 体系中加入一定量的各种组份, 可计算方程系数b1、b2、b3、b4, 如表 1, 其中1-1至1-4为运用(3)式S关于x(Nd)的平衡方程, 2-1至2-4为运用(3)式W关于x(La)的平衡方程。
| 表 1 一元高次方程系数 |
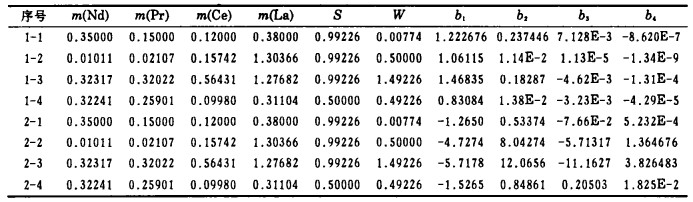 |
| 点击放大 |
萃取体系达到平衡后, 第j组份在水相的平衡值应满足x(j)∈(0, m(j)。
设v(c)为函数方程f3=0在x(j)=c时的函数f3及其一阶、二阶、三阶、四阶导数值的正负号变更次数, 则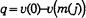
| 表 2 方程在取值区间内实根的数量 |
 |
| 点击放大 |
若q≠0, 可取(0, m(j))中任意一点为方程的初始值x(j)0。
方程(6)在(0, m(j))内存在实根时, 计算过程中不再讨论牛顿法是否收敛, 根据迭代次数决定是否中止计算, 方程(6)的牛顿迭代公式为:

|
(7) |
设计牛顿迭代计算程序对表中数据进行处理, 初值点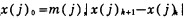
| 表 3 槽体平衡成分计算值 |
 |
| 点击放大 |
2.2 非线性方程组求解
方程(1)、(2)、(3)组成的非线性平衡方程组可以写成:

|
(8) |
定义目标函数:
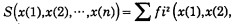
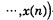

|
其中Fx(1)为雅可比矩阵, 且Fx(1)不等于0, 迭代公式:

|
这是解非线性平衡方程组常用的高斯-牛顿最小二乘法, 它对初始解要求严格, 改进的牛顿法引入修正迭代公式Xk+1= Xk-λ·ΔXk, 本文λ为0.2j(j=1, 2, …, 16)使S(Xk+1) < S(Xk), 即对步长X进行阻尼, 保证了每次迭代目标函数的下降, 加快了收敛速度。
初值为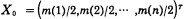
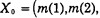
| 表 4 改进牛顿迭代法和高斯-牛顿最小二乘法求解非线性方程组的结果比较 |
 |
| 点击放大 |
3 结果讨论
(1) 从表 2可以看出, 在取值范围(0, m(j))内实根个数均为1, 说明根的存在与理论要求相一致。
(2) 从表 3可以看出, 由x(La)和x(Nd)的方程求解的结果相同。
(3) 无论是关于x(La)或x(Nd)的一元高次方程, 只要esp < 10-7时, 均能达到计算要求, 若存在误差, 即使esp < 10-11, 如表 1中1-4和2-4, 误差仍存在, 由方程(3)计算出ΔW=0.00001, ΔS=-0.00001。除S、W、m(i)外, 将计算变量均设为双精度型数据, 运行结果仍存在误差, 且误差结果一致, 产生误差的原因是因为存在误差传递, 槽体平衡成分计算值是由将一元高次方程符合要求的根代入(4)和(2)式而求得的。设x(j)*为方程(6)的近似解, 根据方程(4)可得到其他平衡水相各组份计算值为:

|
(9) |
根据方程(2)可得到平衡有机相各组份的计算值为:

|
(10) |
E(x(i))、E(x(j))分别为x(i)、x(j)的绝对误差, 根据方程(1)、(2)可得:
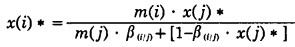
|
(11) |

|
(12) |

|
(13) |
由(12)和(13)式可以看出, ①E(x(i))与E(x(j))同号, 即如果计算x(j)*较真实值x(j)偏小, 则x(i)*较x(i)偏小; ②E(y(i))与E(x(i))异号, 即如果计算x(i)*较真实值x(i)偏小, 则只y(i)*较真实值偏大。
由(3)式可知, x(i)*引起W的偏差:

|
由x(i)*引起萃取量S的偏差:

|
计算机模拟萃取动态平衡计算时, S、W为常量, 由于计算误差的引入和累积, 将造成动态平衡计算结果不符合槽体的平衡状态。
(4) 从表 4可以看出, 在初值为取值范围的中点时, 高斯-牛顿最小二乘法并不发散, 说明初值取值合理, 虽然序号4-4的成分计算出现误差, 但在同一S(X)时, 迭代次数较改进牛顿法小, 这是因为改进牛顿迭代法对X的步长进行阻尼。对改进牛顿迭代法, 改变初值为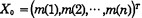
(5) 计算机求解方程得到的只能是方程的近似根, 本文计算过程以计算的S*和W*是否与给定的S和W相等来评价计算的精确度, 根据方程(3), 由表 3和表 4可以计算出各种条件下的平衡状况, 虽然ΔS=0, ΔW=0, 但平衡成分略有不同, 如1-3与2-3, 计算过程允许出现这样的偏差, 并不影响槽体动态平衡模拟计算。
(6) 从表中的计算数据可以得出, 初值为理论取值范围的中点, 采用改进牛顿迭代法进行溶剂萃取槽体平衡成分的计算比较好, 尤其对多组份槽体平衡的计算, 采用改进牛顿迭代法较间接用一元高次方程求解平衡方程组更具优势。
| [1] |
李标国, 李俊然, 严纯华, 等. 串级萃取理论(VI)两组份串级萃取体系动态平衡的研究[J].
稀有金属, 1985, 4(3): 17–22.
|
| [2] |
张圣华.
C语言数值算法[M]. 北京: 海洋出版社, 1993: 346-383.
|
 1998, Vol. 12
1998, Vol. 12
