| 选矿工艺粒度测试数据处理 |
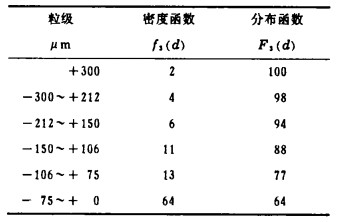
某铁矿精矿进行粒度测试时,从300μm到75μm采用筛分分析,-75μm使用沉降技术粒度分析,其粒度分布数据分别如表 1和表 2所示.据表 1和表 2之1、2、3项数据可绘制出图 1。处理方法如下:
| 表 1 筛析表 |
 |
| 点击放大 |
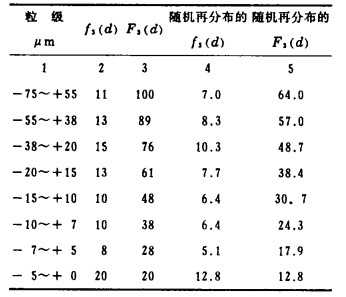
| 表 2 沉降技术粒度分析表 |
 |
| 点击放大 |
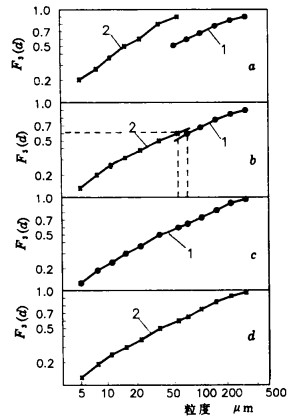 |
| 1.筛分分析散点; 2.沉降分析散点。 图 1 两组粒度分布数据的处理与变换 |
(1) 根据沉降分析的结果,将-75μm的物料进行随机再分布,其质量平衡式为:
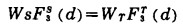
|
(1) |
式中:WS——沉降分析试样重量;
F3S(d)——沉降分析试样中小于某一粒级(d)的累积产率;
WT——试样总重量;
F3T(d)——总试样中小于某一粒级(d)的累积产率。
则
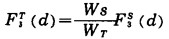
|
(2) |
由表 1筛析数据可知,-75μm的微细物料为试样总量的64%, 于是,
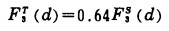
|
(3) |
将沉降分析曲线中每一散点的F3S(d)值按式(3)进行计算,就可得出总试样中相应散点的F3T(d)值(如表 2之4、5项所示)。再连点成曲线,就得到两条大致平行而相互间隔的曲线变换成一条完整的粒度分布曲线(如图 1之b)。
(2) 利用形状系数转换, 将两条具有一定间隔的曲线变换成一条完整的粒度分布曲线。
两条曲线之所以有一定间隔, 是因为筛分分析与沉降分析所测试的粒度变量不同之故.通过观测, 该铁矿精矿矿粒呈不规则的多角形体. П.B.Лященкo通过试验得出[1], 当物料为多角形时, 有:
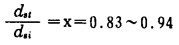
|
(4) |
式中: dst——Stokes径;
dsi——筛分径;
x——形状系数。
对本试料而言, 其x的具体数值可以通过图 1之b的F3(d) = 0.60处划一条直线来确定, 由相应交叉点的dst和dsi值求得:
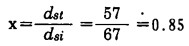
|
(5) |
注意: ①如要考查磨矿细度问题, 按所希望控制的工艺过程, 应当得到一条完整的筛析粒度分布曲线, 则将图 1之b中沉降曲线上的每一个dst点转换成为相应的dsi值, 就可得到如图l之c所示的筛析粒度分布曲线. ②如要考查选别工艺问题, 则将图 1之b中筛析曲线上的每一个dsi点转换成为相应的dst值, 就可以得出如图 1之d所示的沉降分析粒度分布的曲线。
2 不同仪器对微细物料粒度测试数据的变换处理微细物料(粉体)在大多数情况下, 其粒度分布特性符合对数正态分布特征[2]。对数正态分布的密度函数为:
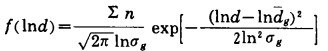
|
(6) |
式中: dg——几何平均值;
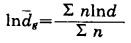
|
(7) |
σg——几何标准偏差;
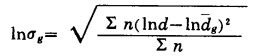
|
(8) |
设Σn = 100 % = 1, 则
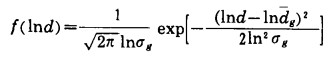
|
(9) |
其分布函数为:
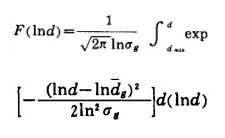
|
(10) |
借助于在对数正态概率格纸上绘制线图, 不仅能判断粒群的粒度分布是否符合于对数正态分布规律(如服从则在该坐标纸中标出的测定值散点必定在一条直线附近), 而且还能得出对数正态分布的两个重要参数lndg和lnσg。
dg的确定:
经标准化后, 应用正态分布表作计算可得:
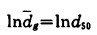
|
(11) |
式中: d50——粒群的中位直径, 它表征了粒群的粗细程度.从图 2可知, d50就是筛下累积为50 %处所对应的粒径。
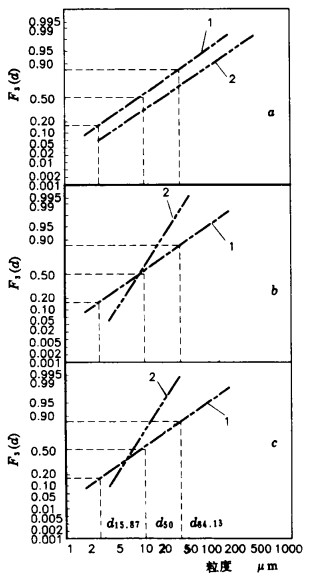 |
| 1.指令的作为对比的“标准”方法所测得的数据; 2.任一方法(仪器)所测得的数据。 图 2 多种方法(仪器)测试数据的对比与变换 |
σg的确定:
通过同上方法计算, 可得:
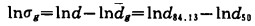
|
(12) |
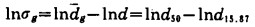
|
(13) |
σg是直线的斜率, 它表征了粒群粒度分布的均匀程度.从图 2可知, d84.13和dl5.87分别表示筛下累积为84.13%和15.87%所对应的粒径。
不同类别的检测仪器, 由于测定机理的不同和所测得的粒度变量、直径类别的不一样, 即使是对同一试样进行检测, 其测试结果是截然不同的, 但却有共同的粒度分布特征, 即对数正态分布规律.任一测试仪器与人为指令的“标准”仪器对比, 在对数概率格纸上是不同的两条直线, 其情况可分为3种(图 2) :
(1) 两条直线平行或近似平行(图2a), 说明σg相同, 但d50。却不相等, 它们之间可以建立:
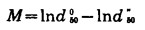
|
(14) |
式中: lnd500、lnd50"—分别是人为指令的“标准”仪器和被比较仪器测得的中位径的对数值;
M—被比较仪器中位径的修正系数。其值在对数概率格纸上的含义是被比直线在纵轴方向平移一段距离, 与其“标准”线重合。通过这样的变换, 两种结果就可以有机地联系起来。
(2) 两条直线相交, 且交点在lnd50, 处(图 2b), 就说明lnd50相等, 但lnσg环一样, 它们的斜率分别为lnσg0和lnσg'。
令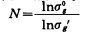
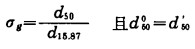
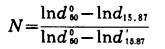
|
(15) |
式中:lnσg0、lnσg'——分别表示人为指令的“标准”仪器和被比较仪器所测得的直线斜率;
lnd15.870、lnd15.87'——分别表示“标准”仪器与被比较仪器所测得的筛下累积为15.87 %处所对应的粒径的对数值.
N—被比较仪器的斜率修正系数.其值在对数概率格纸上的含义可理解为以d50.为中心, 被比直线转动一个角度, 使其与“标准”线重合.
(3) 任意两直线相交, 实际上是前述两种情况的综合(图 2c).
由式(9)可知
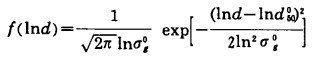
|
(16) |
式中: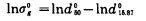
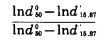
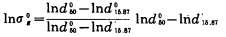
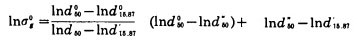
将N、M值代入上式, 可得:
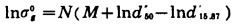
|
(17) |
将式(17)代入式(16), 可导出:
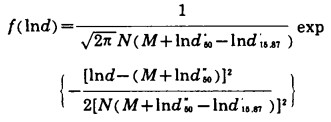
|
(18) |
式中: M = 0时, 说明d50=d50", 两条直线有共同的d50;
M > 0时, 被比直线应向右平移;
M < 0时, 被比直线应向左平移;
N = 1时, 两条直线平行;
N > 1时, 被比直线需顺时针旋转;
N < 1时, 被比直线需逆时针旋转.
M、N值的综合含义实际上说明了两个不同函数间的关系。例如沉降系列检测方法中的Andreosen移液管测定值是以粒度变量为Stokes径dst的函数, 而利用光透原理的检测仪器测定值是以粒度变量为横截面积的投影面径ds的函数, M、N值就是表示这两个函数间的数量关系以及仪器本身的特征值。
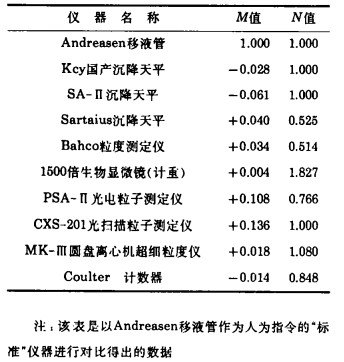
国内10余个单位曾用国内外粒度分析仪器对指定的同一白刚玉微粉试样进行粒度测试得出的分布规律都符合对数正态分布特征。将各种仪器所测得的分布数据在对数概率格纸上打点连线, 并找出其中位径d50和特征值dl5.87, 通过上述坐标变换, 就可得出各种不同仪器对该白刚玉粉的M、N值, 如表 3所示。
| 表 3 仪器对白刚玉粉进行粒度测试的M、N值 |
 |
| 点击放大 |
这种变换方法将给我们的科研工作带来较大的好处.例如絮凝分选, 根据工艺要求进行粒度测试时其粒度变量应为Stokes径, 若使用激光粒度测试仪, 因其所测得的粒度变量为投影面径, 不符合工艺要求.为解决这一矛盾, 可以预先通过相应的测定, 求出其M、N值, 在往后的激光粒度测试中, 就可轻而易举地将投影面径分布变换成为Stokes径分布了.
3 结论(1) 采用随机再分布和形状系数转换法对筛析和水析的粒度测试数据进行处理, 可以将原两组似乎没有任何联系的密度函数或分布函数变成一条连续的粒度分布曲线。用此来表示物料的粒度分布特征, 才显得圆满而完整。
(2) 使用被比较仪器的中位径和斜率修正系数对粒度分布函数进行坐标变换, 就可将A种仪器所测得的粒度分布(包括粒度变量)变成B种仪器的粒度分布数据。这就使我们检测的粒度分布(包括粒度变量)尽可能反映出所希望控制的工艺过程的要求。这种变换方法将给科研工作带来一定的便利。
| [1] |
Herbst J A, Sepulveda J L. 粒度分析[J].
国外金属矿选矿, 1981(5): 11–12.
|
| [2] |
卢寿慈.
矿物颗粒分选工程[M]. 北京: 冶金工业出版社, 1990: 33-39.
|
 1997, Vol. 11
1997, Vol. 11
