| 特解边界元法在充填采矿法中的应用 |
2. 南方冶金学院, 赣州 341000
2. ${affiVo.addressStrEn}
在初始地应力场已知的条件下,用边界元法进行工程计箅时,不仅要将初始应力场与释放应力场叠加,同时要增加由岩体自重引起的体力项,处理体力问题的方法有域内积分法、边界积分法等,用特解边界元法处理体力项不需要在域内剖分单元,只需在无体力项的边界元程序中稍加修改即可.该程序是在文献[2]给出的边界单元直接法分析弹性静力学平面问题程序的基础上改编的,该程序有较强的通用性,可分析各种边界条件下的内部问题或外部问题;同时采用区域耦合的方法,可方便地解决考虑充填体自重的充填采矿问题.本文仅讨论线弹性问题,其方法可推广到粘弹、粘塑性问题上。
1 基本原理[3]对于平面静弹性力学问题有平衡方程:

|
(1) |
式中:Bi——体力项.
以下记齐次方程的解用右上角C表示,特解用右上角P表示,则有:
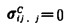
|
(2) |
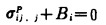
|
(3) |
若方程(2)、(3)已经解出,则根据线性微分方程理论,方程(1)的解可表示为:
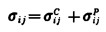
|
(4) |
进而有位移解和面力解:
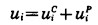
|
(5) |
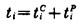
|
(6) |
将方程(5)、(6)引入(2)式的边界元方程则有:
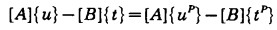
|
(7) |
式中[A]、[B]为边界影响系数矩阵,引入实际问题的边界条件解此方程组即可求得待解问题的边界节点的实际位移及面力;将(5)、(6)引入方程(2)式的域内点求解公式,即可求得域内点实际位移和应力。
2 充填采矿中特解边界元求解方法 2.1 特解的求算假定原始应力场最大主应力为垂直向下方向,按岩体自重计算体力项特解为:
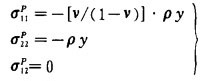
|
(8) |
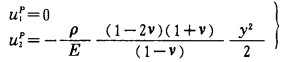
|
(9) |
式中:E——弹性模量;
v——泊松比;
ρ——容重。
面力通过关系式tiP=σijPnj求出。
假设胶结充填体之间接触紧密,为无摩擦接触,可将充填体在其子域内视作均质的,体力特解仍由公式(8)、(9)给出,其力学参数由实验给出。值得说明的是,对于松散充填体,由于其粘结力为零,起始压缩模量较小,此时再将整个充填体视作连续均质弹性体与实际有较大出入,对该问题尚待进一步研究。
2.2 充填体与围岩的区域耦合用Dancan反转应力释放法可建立硐室与充填体的边界元方程[4]为了模拟围岩与充填体自重,将充填体部分视为子域进行多区域耦合处理,这样处理有着明显的优点,首先不会增加过多的计算量和理论推导,其次可方便地对充填体参数进行调整。
如图 1所示,将求解域分为充填体部分Ω1和围岩部分Ω2, C1, C2分别为Ω1的外边界和围岩的内边界,根据Dancan反转应力释放法原理结合应力相等位移协调的边界条件可得出硐室、充填体的边界方程[4], 对此方程进行特解项处理可得如下方程:
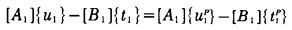
|
(10) |
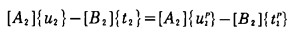
|
(11) |
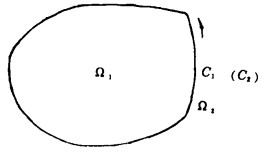 |
| 图 1 子域示意图 |
式中:下标1、2表示对边界C1、C2的分量,{u1}、{t1}分别表示在C1交界面单元上的位移分量和面力分量, [A1]、[B1]表示在C1交界面上影响系数矩阵。{u2}、{t2}、[A2]、[B2]含义类推。引入交界面连续条件:
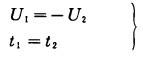
|
(12) |
对(10)、(11)式进行数学处理,将得到以待解边界值为未知量的线性代数方程组。
3 应用实例 3.1 研究对象及目的某铜矿一主要矿体倾角40~45°, 平均水平厚度14.69m, 围岩以花岗斑岩为主。该矿体东部地表有农田,西部地表有溪流经过,为防止矿体与溪流发生水力联系而引起地表塌陷,需对采空场的稳定性作出评价,现对有代表性的-235m中段采空场充填前后围岩性态变化进行特解边界元计算分析。
3.2 力学参数及计算模型对该矿山现用的尾砂胶结充填料进行了力学参数测定试验,围岩的参数由矿山提供,见表 1。
| 表 1 岩体、充填料有关参数 |
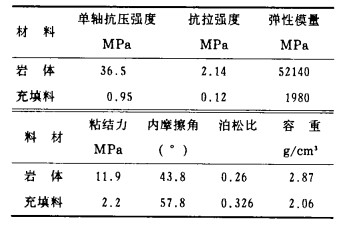 |
| 点击放大 |
取垂直矿体走向为计算剖面,如图 2所示.Ⅰ、Ⅱ线为待求位移点所在位置,计算中假设充填体无初始应力且为接顶充填。
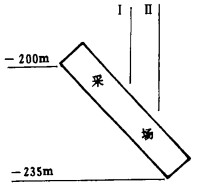 |
| 图 2 计算采场剖面图 |
3.3 主要计算结果及分析
为了比较采场充填前后围岩应力分布特点,图 3、图 4给出了围岩主应力等值线图。
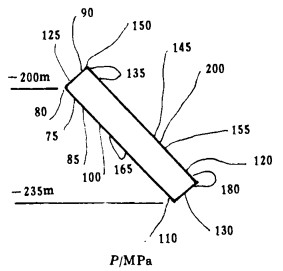 |
| 图 3 充填前主应力等值线图 |
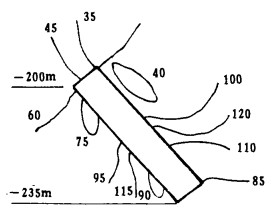 |
| 图 4 充填后主应力等值线图 |
由上述计算结果可知:
(1) 采场充填前应力集中区域主要在顶、底板右侧,上盘中部偏下的部位,同时与上盘相对的下盘位置也有局部应力集中;以主应力数值上分析,其最大值为200 MPa, 是岩体单轴抗压强度的5倍以上;尤其值得注意的是上盘围岩出现了局部拉应力,导致围岩的拉伸破坏。
(2) 采场充填后,与充填前相比应力集中现象得到明显的改善,最大主应力值下降了近一半,顶、底板主应力值下降尤为显著.充填体的支撑作用使得拉应力数值及范围减小,仅在上盘中部小范围内有拉应力。
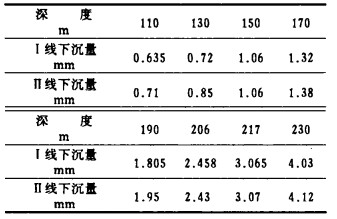
上面分析表明采场围岩主要破坏部位在上盘中部,为了进一步找出围岩下沉规律,在上盘沿Ⅰ线、Ⅱ线(如图 2所示)分别计算了若干点的垂直位移值,限于篇幅,这里仅给出充填后的部分计算结果,如表 2。
| 表 2 位移值部分计算结果 |
 |
| 点击放大 |
对围岩下沉量与深度的关系进行回归分析可得出下面公式:
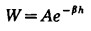
|
(13) |
式中:W——下沉量,单位:l0-5m;
h——深度,单位:m;
A、β——回归系数。
计算结果表明:系数A、β随着所取垂线距采场水平距离的不同而不同,当所取垂线位置定下后,A、β就成为定数,对Ⅰ线:A= 32.79, β=—0.0093 5;对Ⅱ线:A=53.289, β=0.00792.除Ⅰ、Ⅱ线外,还可再取若干垂直计算线,结果表明:从地表至地下90m范围内,围岩下沉量最大值均不超过0.4mm, 说明当采场充填后,围岩破坏不会影响到地表。
4 结论特解边界元法可以方便地解决考虑围岩及充填体自重的充填采矿问题,采用该方法较成功地应用在倾斜采场围岩稳定性分析中,通过计算分析得出了一些结论。
(1) 充填前采场的上盘中部及顶、底板右侧为主要破坏部位。
(2) 使用具有一定强度的充填体后,充填体的支撑作用将使应力集中缓和,主应力值下降,岩体破坏部位主要集中在上盘中部小范围内。
(3) 由于边界元法具有计算任意内点值的优点,可方便地找出围岩下沉规律。
上述结论对相似条件下的矿山具有一定的参考价值。
| [1] |
孙钧, 韦永盛.
岩石力学新进展[M]. 沈阳: 东北工学院出版社, 1989: 1-21.
|
| [2] |
Crouch SL, Starfield AM.
Boundary Element Method in Solid Mechanics[M]. London: George Allen and Unwin, 1983.
|
| [3] |
李庆斌, 周鸿钧, 林皋, 等.
特解边界元法及其工程应用[M]. 北京: 科学技术文献出版社, 1992: 59-69.
|
| [4] |
叶黔元. 边界元法在充填采矿法中的应用[J].
江西冶金学院学报, 1985(3): 12–17.
|
 1997, Vol. 11
1997, Vol. 11
