| 预裂爆破参数计算原理 |
2. 中南工业大学, 长沙 410083
2. ${affiVo.addressStrEn}
众所周知, 预裂爆破应用时, 一般采用工程类比、模拟试验、现场小型试验以及采用经验、半经验公式和理论计算等方法来确定其参数。但因岩石条件多变, 如岩石的抗拉、抗压、抗断裂等强度不同, 岩石的不均质性、各向异性等, 以及不同区域地应力和地质构造的影响, 都给预裂爆破参数的合理确定带来了极大困难。所以, 如何针对不同的岩性和条件合理确定预裂爆破参数, 已为爆破界人士广为关注, 并为此作了卓有成效的尝试。据此, 本文拟在预裂爆破断裂机理研究的基础上, 建立其断裂模型, 推演一种新的计算方法, 试图为实际工程应用提供参考。
1 预裂爆破断裂原理工程爆破中的岩体, 一般存在有节理裂隙之类的宏观裂纹, 又具有晶粒分界面之类的微细裂纹。据Bienawski通过显微照相观测, 认为许多晶粒分界面相当于小裂纹, 其长度af的变化范围大致为0.0025~0.025cm。而低应力脆断的大量分析研究表明, 脆性破坏总是由介质中的缺陷或裂纹的快速扩展引起的。所以, 扬弃以往预裂爆破理论计算中关于被爆介质中不存在缺陷或裂纹的假设, 而把被爆介质看成是连续和间断的统一体, 即利用断裂力学原理来研究预裂爆破、的断裂过程, 有可能在原有理论计算上进一步切合工程实际。
在预裂爆破断裂原理方面, 传统弹性力学分析, 把被爆介质看成是均质、连续、各向同性的, 只考虑应力因素, 达到应力强度时就破坏, 即破坏是从应力最大点开始的。爆破试验表明, 对于水泥砂浆这类模型材料, 在爆炸作用下, 介质的破坏并不全是从应力最大点开始的。从而说明介质的内部缺陷对爆破破坏有重要影响。其次, 爆破时裂纹扩展是介质破坏的基本过程, 裂纹的发生和扩展意味着材料状态的改变, 它破坏了弹性力学和塑性力学的连续条件。所以, 应用各种立足于物体应力状态的强度理论来进行预裂爆破参数的计算, 已很难满足工程爆破的实际需要。鉴于此, 预裂爆破可以应用断裂力学的基本原理, 对其参数的计算进行理论推演, 导出计算公式。
预裂爆破炮孔是在主爆孔之前爆破成缝的, 而炮孔直径与孔间距、炮孔深度和抵抗线值相比很小, 所以可以将炮孔两侧视为无穷大介质。在此约束条件下, 对于预裂炮孔的断裂机理可以作如下解释:预裂爆破一般采用圆柱状不耦合装药, 由于不耦合效应的影响, 爆生气体与环状空气介质的分界面附近出现的脉动和涡流, 使得爆生气体和被压缩空气在开始时是混在一起向外推进, 因而作用于预裂孔壁上的动态应力应该同时包括爆炸冲击波和爆生气体膨胀推力的综合作用。当其综合应力小于介质的动态抗压强度时, 炮孔周壁不会被压碎, 但受切向拉应力作用, 因其抗拉强度远小于其抗压强度。所以, 炮孔周壁会产生径向裂缝。所谓预裂爆破, 是指多个预裂孔的爆破, 而非简单的单孔爆破, 所以炮孔之间的相互作用甚为重要, 亦是解释预裂孔断裂的关键所在.爆破试验表明, 预裂爆破时介质中应变持续的时间为4ms左右, 说明爆炸应力波向四周传播衰减后, 在一定介质区域内形成的应力状态不是随之立刻消逝的。所以预裂爆破在一定的时间间隔内炮孔与炮孔之间爆炸应力叠加是存在的。炮孔连心线方向的切向拉伸应力叠加形成应力的加强区, 其它方向则或多或少地形成应力的减弱区, 因而, 炮孔连心线方向则优先受到拉伸应力作用而形成较长的初始径向裂纹。其次, 预裂炮孔周壁存在有许多天然随机分布的介质晶粒界面类的微细裂纹, 在相邻炮孔的爆炸应力作用下, 若其驱动应力强度因子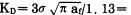
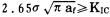
预裂爆破, 因炮孔直径dc与孔间距E、孔深L、最小抵抗线W相比甚小, 所以预裂爆破的断裂可以简化为无穷大介质中的平面应变断裂。岩石断裂初期, 可以用弹性力学建立判据, 当形成一定长度的裂逢之后, 可以用线弹性断裂力学(LEFM)建立判据。
预裂爆破时, 裂纹的形成和扩展, 改变了炮孔周围的应力应变状态, 着重考虑裂纹尖端的应力应变状态, 是分析其断裂模型的关键。无论是动应力还是准静应力, 均是以应力强度因子的形式施加于裂纹尖端, 当KD≥KIC时, 则裂纹快速扩展, 介质呈脆性断裂。爆炸作用下的应力场较为复杂, 介质除受拉伸应力作用外, 还受到剪切、挤压等作用, 但由岩石特性知, 拉伸破坏更易于发生, 因为岩石的抗拉强度仅为抗剪抗压强度的(1/8~1/14)。再者, 有关爆炸作用下复合型应力强度因子的研究表明, | KⅠ/KⅡ|之值较大(约为10)(KⅠ张开型; KⅡ剪切型), 且变化范围较大, 即爆炸时裂纹尖端拉伸作用比剪切作用大得多。所以, 可以认为, 预裂爆破的断裂主要是受张开型(Ⅰ型)应力强度因子KD控制。因此, 预裂爆破参数计算中主要是考虑Ⅰ型应力强度因子的作用, 并依此建立断裂判据。
3 计算原理预裂爆破中, 预裂孔的不耦合系数Ku、装药密度Δ、孔间距E等是其主要参数。为使获得较为理想的预裂爆破效果, 除合理确定主要参数外, 还应考虑介质的力学性质、炸药性能、地质构造等, 这给预裂爆破实施带来了困难。作者拟依据所阐述的预裂爆破断裂机理和建立的模型, 推演出主要参数的计算公式, 为实际应用提一种新的确定参数方法。
根据凝聚炸药爆轰的C-J理论可知, 炸药爆炸时, 爆炸气体的初始平均压力为:
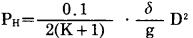
|
(1) |
式中:PH—爆炸气体初始平均压力, Pa;
K—炸药的等熵指数;
δ—炸药的容重, g/cm3;
g—重力加速度, m/s2
D—炸药的爆速, m/s
爆炸气体膨胀过程的状态方程可表述为:
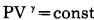
|
(2) |
式中:P—爆炸气体膨胀过程中的压力, Pa;
V—气体膨胀过程中的体积, cm3;
γ—气体绝热膨胀指数, 取γ=1.4。
设爆炸气体膨胀至孔壁时的压力为P2, 对应于P2和PH的气体体积分别为V2和VH, 则依(1)、(2)式有:
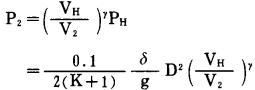
|
(3) |
预裂爆破时, 必须保证爆破产生的动态综合压力对炮孔不致压碎破坏, 因而炮孔的综合压力Pc应满足一个基本条件:
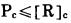
|
(4) |
式中:[R]c—矿岩的动态抗压强度, Pa; 依A、H、哈努卡耶夫的试验, [R]c=(10~12)[σ ]c, [σ ]c为矿岩的静态抗压强度, Pa。
而作用在预裂孔壁的综合压力值为:
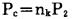
|
(5) |
式中:nk—气体与孔壁碰撞时压力增大系数; nk=8~11。
因为
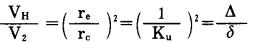
|
(6) |
式中, Ku—装药不耦合系数, Ku=rc/re;
Δ—炮孔体积装药密度, g/cm3。
联立求解(3)、(4)、(5)、(6)得:
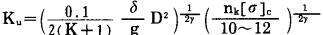
|
(7) |
将(7)式中, 取[R]c=10[σ]c, nk=10, K=2.8, g=9.8m/s2, δ=1.0g/cm2, γ=1.4, 计算得:
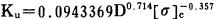
|
(8) |
现场试验中, 若使用2#岩石硝铵炸药, 则D=3200m/s(ϕ =32mm)。
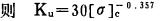
|
(9) |
式(8)说明, 预裂爆破时不耦合系数Ku与炸药的爆速D的0.714次幂成正比, 而与岩石的抗压强度的0.357次幂成反比。对于不同的矿岩条件, 将式(9)的计算结果列于表 1, 并绘成曲线如图 1所示。
| 表 1 不同矿岩条件下对应的K u值 |
 |
| 点击放大 |
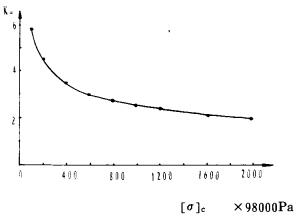 |
| 图 1 预裂爆破时不耦合系数Ku与矿岩抗压强度[σ]c之间的关系曲线 |
将式(9)代入式(6)得最大允许的体积装药密度: Δ= δ/900[σ]c-0.714
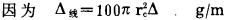
|
(10) |
所以, 最大允许的线装药密度:
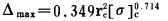
|
(11) |
式(11)说明, 预裂爆破时最大允许线装药密度与炮孔半径rc的平方和介质的抗压强度[σ]c的0.714次幂成正比。若孔径确定后, Δmax主要取决于[σ]c0.714之值
若炮孔直径dc =20cm(rc=10cm), 则
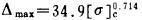
|
(12) |
将式(12)的计算结果列于表 2, 并绘成曲线如图 2所示。
| 表 2 不同矿岩条件下对应的Δmax值 |
 |
| 点击放大 |
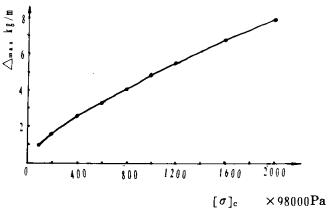 |
| 图 2 预裂爆破(rc=10cm)线装药密度Δ线与矿岩抗压强度[σ]c之间的关系曲线 |
Δ线、Ku和孔间距E是互相联系的, 所以孔间距E的计算, 应综合考虑Δ线和Ku等的影响。预裂爆破时, 由应力波的传播规律可知:
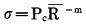
|
(13) |
式中:R—比例系数, R=r/rc, r为应力波传播半径, cm。
m—应力波衰减系数。
爆炸试验测试表明, 预裂爆破时应力波在介质中传播时的衰减系数, m=1.42, 而大冶铁矿现场测试表明, 在矿石、大理石、闪长岩中应力波衰减系数分别为1.39、1.48、1.56。所以, 计算时, 可以近似选取m=1.42。
预裂爆破时, A、B两孔断裂计算示意图如图 3所示。
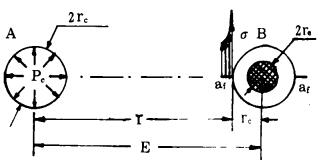 |
| 图 3 预裂爆破时孔距E计算参数示意图 |
A、B两预裂孔爆破时, A孔的爆炸应力被传至B孔壁时, 在B孔壁沿AB连心线方向产生切向应力集中, 当其驱动应力强度因子KD大于介质的KIC时, B孔开始扩展朝AB连心线方向的微细裂纹af, 从而控制了B孔的断裂方向。本文认为, 此时确定的A、B两炮孔之间的孔间距E, 即为形成预裂爆破的有效孔间距。依前述预裂爆破断裂的原理, 有如下判据。
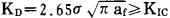
|
(14) |
将式(13)代入式(14), 令Kn=KIC, 求解得
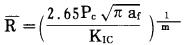
|
(15) |
式(15)物理意义表明, 预裂爆破时比例系数(R=(E-rc)/rc)与炮孔压力Pc的1/m次幂和介质中微细裂缝长度af的1/2m次幂成正比, 与介质的断裂韧性KIC的1/m次幂成反比。所以, 对于确定的介质和炮孔装药密度就有与之相应的有效孔间距E。若选取预裂爆破的临界状态, Pc=[R]c, 则可以求得最大的比例系数Rmax。
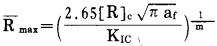
|
(16) |
所以, 预裂爆破时最大孔间距Emax为Emax=(Rmax+1)rc。
为了验证式(16)的实际意义, 将Schmidt所测花岗岩参数; af=0.075cm, KIC=261kg/cm3/2, [σ]c=137.2MPa, 并取m=1.42, [R]c=(10-12)[σ]c代入上式计算得:
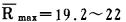
|
对砂岩, Atkiuson测得:af=0.05cm, KIC=140kg/cm3/2, [σ]c=98.0Mpa, 并取m=1.42, [R]c=(10~12)[σ]c, 代入式(16)计算得:
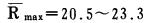
|
从而说明, Emax=(Rmax+1)rc=(20.2~24.3)rc=(10.1~12.2)dc, 即预裂爆破时最大孔间距可取10~12倍炮孔直径。而一般经验表明, 预裂爆破时孔间距E可以取8~12倍炮孔直径, 显然式(16)所确定的参数与实际结果是相吻合的。
本文所确定的计算原理认为, 对于一定的爆破介质, 可以确定最大的比例系数Rmax来实现预裂爆破, 当所选用的孔间距与炮孔半径之比超过Rmax+1时, 将难以获取理想的预裂爆破效果。对于选定的孔间距E(E≤Emax小有与之对应的合理的装药密度, 可以用式(15)反算求得。预裂爆破所允许的最小不耦合系数是由炸药特性和爆破介质特性所决定的, 当不耦合系数不小于允许的最小Ku时, 则炮孔不会被压碎, 必然有与之相对应的合理的Δ线和R值。
4 结语a.预裂爆破的断裂机理应着重考虑预裂孔之间的相互作用, 爆炸应力的持续状态和应力集中对相邻炮孔沿炮孔连心线方向的微细裂纹af的扩展有重要影响, 从而为预裂面的最终形成创造了初始必要条件。
b.不藕合系数Ku的理论计算表明, 在介质抗压强度[σ]c=39.2~196.0MPa时, 合理的Ku值为3.5~2。
c.预裂孔的Δmax=0.349rc2[σ]c0.714, 当炮孔直径dc=20cm时, Δmax=0.93~1.5kg/m, ([σ]c=9.8~19.6MPa), 试验结果Δ=1.05~1.5kg/m, 两者很接近。
d.预裂爆破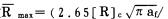
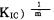
e.爆炸试验表明, 应力波在介质中传播时衰减系数m一般在1.39~1.56之间, 一般试验值为m=1.42。该值介于弹性介质强间断波的传播m=0.5和准静态分析m=2之间。
f.对于一般预裂爆破爆破工程(无特殊要求), 在确定合理的预裂爆破参数时, 建议选取Kumin、Δmax、Rmax所确定的数值, 据此, 可以获取较佳的经济效益。
 1995, Vol. 9
1995, Vol. 9
