| 岩石裂纹扩展的力学分析 |
2. 石油大学石油工程系, 北京 102200
2. ${affiVo.addressStrEn}
在分析不连续岩体的边坡、地基、大现以及地下工程的稳定性时,通常假设整个结构面是连续的,忽略了在不连续裂纹顶端的应力集中。如研究边坡稳定性最常见的一种方法就是考虑成共面的破坏带,而未考虑岩体结构内部的不连续面。对给定几何形状的岩体工程,岩体应力随岩体大小的增加而增大,岩体强度随岩体大小的增加而降低。对于小型岩体工程,从断裂力学分析表明:由初始裂纹扩展所产生的连续多级破坏面,当进一步发展时所需要的剪应力较裂纹初始扩展时低。运用于分析岩体工程稳定性的断裂力学模型更能真实地反映其破坏机理。
为了分析岩体工程中裂纹扩展的特性,必须考虑岩体抗拉强度及抗剪强度的影响。因为这两个强度对不连续岩体中位移的发展都起到阻尼作用。其中,抗拉强度控制着拉应力带及边坡或大坝等岩体工程地面露头的分离,而剪切强度对岩体工程的平衡稳定提供了阻力。现分述如下。
1 岩体抗拉强度对裂纹扩展的阻尼作用岩体抗拉强度比其抗压强度小得多.但是在不连续裂纹处抗拉强度是很重要的。对于单一裂纹,裂纹开始扩展时所施加在岩体上的单向拉应力表达式为:

|
(1) |
式中KIC—拉应力强度因子;
a—裂纹长度的一半。
上式也可写为:
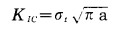
|
(2) |
对于垂直于一组等间距共面裂纹施加拉应力的情况,岩体的强度σt,为:[1]

|
(3) |
式中:2b——裂纹中心距。
当初始裂纹向纵深发展贯穿岩体工程的自由表面时也会出现破坏带,在裂纹扩展过程中,裂纹顶端作为其扩展的前缘,岩石的内聚力对其扩展起着一种阻尼作用。就是说.在裂纹顶端的小区域内,裂纹表面相距很近,两表面间分子或原子间的内聚力未完全消失,它是一个不可忽略的内力。
如图 1所示,根据Barenblatt提出的内聚力模型,可以写出内聚力c(x)所对应的应力强度因子K'I:
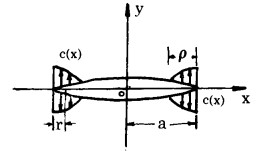 |
| 图 1 内聚力模型 |
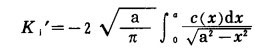
|
(4) |
由于c(x)只是在裂纹端部很小的局部区域ρ内存在,且ρ«a, 因此r≤ρ≤a, a2-x2 = (a+x)(a—x)=(2a—r)r=2ar,r系以分子错位点为起点的内聚力衰减距离,r∈[0, ρ]。
将上述关系代入(4)式,并变换积分变量得:
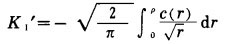
|
(5) |
从上面的分析可以看出,内聚力c(x)的存在阻碍了裂纹的扩展,消除或降低了裂纹顶端应力的奇异性,其作用效果与拉应力作用下的效果相反,于是起到了降低裂纹拉应力强度因子KⅠ,的作用。将(5)式与(2)式相加可得考虑裂纹顶端内聚力c(x)作用下的拉应力强度因子:
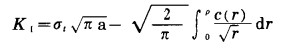
|
(6) |
裂纹的剪切强度是作用在裂纹面Ji法向压应力的函数,而垂直于破坏面上的法向压应力,其作用是减小了在裂纹顶端的拉应力,因而阻碍了裂纹的扩展。法向压应力也能使裂纹闭合,通过裂纹表面传递部分法向压应力,压应力强度因子KⅠ将会减小。由于闭合的裂纹能够传递剪应力,从而也减小了剪应力强度因子KⅡ。对于扁平裂纹,在法向压应力σn的作用下裂纹的最大闭合量W为:[2]
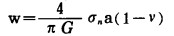
|
(7) |
式中:G, v—分别为剪切模量、泊松比。
裂纹闭合压应力σc可以根据裂纹形态比A来表达:

|
(8) |
式中:A—裂纹形态比,定义为裂纹最大起伏度与裂纹长度之比,由地质资料确定。
不连续节理性岩体中的剪切破坏是由拉应力、剪应力共同作用的结果,其裂纹是复合型扩展破坏,可用KⅠ、KⅡ。两个强度因子共同描述其破坏准则。对于等间距张开型共面裂纹,剪切强度因子为:

|
(9) |
式中:τ-平行于裂纹面的剪切应力。
由裂纹顶端最大拉应力所建立的复合型破坏准则,可以评价在压剪应力共同作用裂纹扩展的条件为:[3]
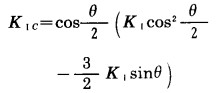
|
(10) |
式中:θ——裂纹扩展的方向与原裂纹平面间的夹角,它满足于下列方程:

|
(11) |
求解上式,可得:
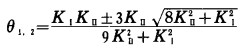
|
(12) |
根据这些关系式及KⅠ、KⅡ的方程,裂纹破坏的条件就可用σ、τ来描述,即:

|
(13) |
式中θ由(12)式得到,即将(6)、(9)式的KⅠ、KⅡ代入(12)式,由此可见角θ也是受应力状态(σ、τ)影响的。
在以上的讨论中假设了裂纹表面保持拉应力自由,当裂纹扩展长度较小时这一假设是合理的。对于非接触啮合(即裂纹两侧起伏面相互啮合,但其间未接触)的裂纹表面,裂纹两侧的起伏面将在发生一定剪切位移后才能紧密接触。当裂纹两侧的分离距离大于表面最大起伏高度时,只有在压应力作用下缩短了部分分离间距时裂纹表面才会接触。在中等形态比率、裂纹较长的情况下,裂纹表面相距可能较大,从而只有在裂纹表面起伏较大而起伏角较小时才会发生表面两侧的紧密接触。如果裂纹表面起伏角较小,出现起伏面紧密接触时所需要的剪切位移将比裂纹长度大得多,这将表明在没有发生大量裂纹扩展的条件下即使较短的裂纹也不会出现紧密接触。最大剪切位移u(最大相对剪切位移的一半)发生在裂纹的中心,从平面应变条件可以导出:
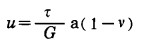
|
(14) |
如果最大剪切位移u相对于裂纹最大宽度较小,那么就不会发生裂纹两侧起伏面的紧密接触,裂纹表面将保持自由拉应力。如果裂纹扩展与初始裂纹贯通而形成多级破坏面,由于裂纹的几何形状随其扩展而发生变化,在裂纹顶端的应力强度因子一般要降低,其结果使相邻裂纹可能在相互贯通之前就处于稳定状态了。
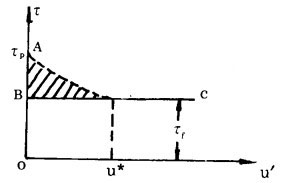
当裂纹受压闭合或因发生剪切位移而紧密接触后,裂纹面间的摩擦应力对裂纹的扩展有着重要的影响。按库伦定律,最大静摩擦力τp正比于裂纹面上的法向压应力σn:
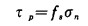
|
(15) |
式中:fs—静摩擦系数。
Palmer A.C.等提出:当接触面开始滑动后,裂纹面上的剪应力τ不是立即从静摩擦应力τp突然降至动摩擦应力τf=fασn(fα为动摩擦系数),而是随着剪切位移u'的增加而逐渐减小,如图 2所示。当u'达到某一临界值u*时,τ才减小到τf, 以后则保持(τf)不变。在此过程中裂纹发生能量释放,从下面的分析中可以看出,图 2中阴影部分的面积就是释放的能量。τp、τf值的大小及曲线的形状由实验测定获得。
 |
| 图 2 摩擦力分析 |
在裂纹端点,u'必定为零,所以该点的剪应力τ等于τp。随着距端点位移x的增如,u'逐渐增大,τ按图 3所示的规律逐渐减小,至距端点x=ω处,u'才达到u*。在x≤u'内τ降至τf,在x>ω之外裂纹面上的剪应力恒为τf。从分析中可以看出,摩擦系数fs及fα也是ω及剪切位移u'的函数。
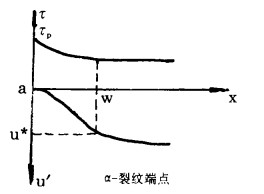 |
| 图 3 裂纹端部应力与位移分布 |
3 剪切断裂能
由于Barenblatt内聚力模型的引入,消除了裂纹端点应力的奇异性,所以裂纹的能量释放率心Jp=0, 从而对裂纹的J积分表达式为:
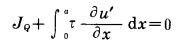
|
如果Q点取在x>ω的范围内,则此式为:

|
(16) |
由上式可知,等式左侧代表相对应的弹性裂纹的能量释放率,右侧恰好是图 2中阴影部分的面积,Palmer等人称之为剪切断裂能,即

|
(17) |
这里仅考虑了裂纹面间的摩擦应力只是相对位移V的函数,实际上它还与滑动速率、含水情况、裂纹面的水理性以及接触时间等许多因素有关。
4 结束语本文详细地讨论了裂纹在拉压应力及剪切应力作用下可能发生的一系列力学效应.得到了以下几点主要结论:
a. 内聚力c(x)的存在阻碍了裂纹的扩展,消除或降低了裂纹顶端应力的奇异性,其作用效果与拉应力作用下的效果相反,于是起到了降低裂纹拉应力强度因子KⅠ,的作用。并得到了考虑裂纹顶端内聚力c(x)作用下的拉应力强度因子:
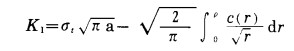
|
b. 不连续节理性岩体中的剪切破坏是由拉应力、剪应力共同作用的结果,其裂纹是复合型破坏,可用KⅠ、KⅡ两个强度因子共同描述其破坏准则。得到了用σ、τ来描述的裂纹破坏条件:
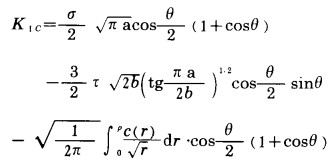
|
c. 当裂纹受压闭合或因发生剪切位移而紧密接触后,裂纹面间的摩擦应力与裂纹的扩展有着重要的影响。
综上所述,诸如开裂扩展、闭合接触、裂纹面上应力的重新传递等,都在不同程度上影响裂纹的拉、剪应力强度因子及其扩展准则。因此,由这些结论建立的断裂力学模型,运用于分析不连续岩体中工程的稳定性机理更可靠、更实际。
| [1] |
黄克智, 佘寿文.
弹塑性断裂力学[M]. 北京: 清华大学出版社, 1985: 10.
|
| [2] |
Thomas M Tharp. Stability of Slopes in Discon-tinously Jointed Rock. 25th U. S. Symposium on Rock Mechanics. 893~901
|
| [3] |
Ingraffea A R. Miced-Mode Fracture Initiation in Indina Limestone. 22 nd U. S. Symposium on Rock Mechanics. 186~191
|
 1995, Vol. 9
1995, Vol. 9
