| 露天矿分期开采综合优化设计方法 |
露天矿采用分期开采, 可以减少早期岩石剥离量, 促使矿山早日投产和达产, 从而大幅度地提高露天矿初期经济效益。因此分期开采是多快好省建设露天矿的重要技术手段。国内外许多大型露天矿常常采用这种开采方式。可见提高分期开采设计水平, 不仅具有很强的实际意义, 而且具有重要的经济意义。
对于露天矿分期开采优化设计, 关键是要解决下列几个关键课题:
a.合理地确定分期开采境界;
b.合理地确定分期开采开拓运输系统;
c.合理地确定分期开采扩帮过渡策略。
上述三个问题是相互影响、相互制约的。合理地解决这些问题, 是进行分期开采优化设计的关键。
1 分期境界动态优化设计方法露天矿分期境界的确定是分期开采设计的重要内容。本文提出了动态浮锥法来确定最优的露天矿分期开采境界。
1.1 动态浮锥法方法在露天矿最终境界确定之后, 每年的矿石产量已确定下来。为了能动态地确定最优的分期开采境界, 本文在标准浮锥法的基础之上, 提出了考虑资金时间价值的动态浮锥法。
1.1.1 基本原理动态浮锥法的基本原理如下:
a.以时间为阶段, 在满足每年矿石生产能力的条件下, 以不同的剥岩量为状态;
b.在一个水平上按最小底宽确定采出范围, 若矿量不够, 则增加深度从上到下依次搜索, 直到满足该年的矿石产量为止。在该水平上继续搜索其它可能满足矿石生产能力的状态, 直到找不到为止;
c.在执行(b)时, 若未进行再次搜索, 矿量已超过该年的矿石生产能力, 则放弃该状态并中止搜索;
d.搜索时, 锥顶放在矿石块上, 该矿石块满足下列条件:
式中:L(I, J)—地形数组。
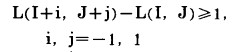
|
(1) |
a.空间状态转移方程 每搜索一次, 开采空间就变化一次。新的开采空间是在旧的开采空间基础之上再进行一次搜索开采之后而形成的。因此, 空间状态转移方程为:
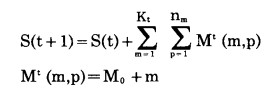
|
(2) |
式中:S(t)—第t年初的地形;
Mt(m, p)—第t年第m水平第p次搜索时的开采锥面;
nm—第m水平的搜索次数;
Kt—第t年内的开采最低水平;
M0—第0水平的开采锥面。
b.数量状态转移方程 由于采矿空间发生变化, 矿石开采量和岩石开采量也发生相应变化。于是矿岩数量状态转移方程为:
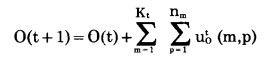
|
(3) |
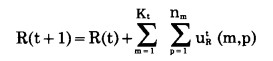
|
(4) |
式中:O(t)、R(t)—分别为第t年初的累计采矿量和累计剥岩量;
uot(m, p)、uRt(m, p)—分别为第t年内第m水平第p次搜索时的采矿量和剥岩量。
c.约束条件 每年搜索出来的矿石量应等于该年的矿石产量, 即
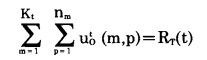
|
(5) |
式中:Rt(t)—第t年的矿石生产能力。
d.目标函数 优化的目标是在开采的年限之内露天矿生产总费用为最小, 即
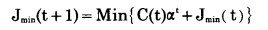
|
(6) |
式中:Jmin(t+1)—从第一年初到第t年初的最小累计生产费用;
C(t)—第t年内的生产费用, 这时采矿量为RT(t), 剥岩量为
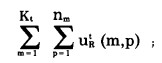
|
α—贴现率。
由于第一年初未进行生产, 因此有
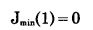
|
(7) |
很明显, (2)~(7)构成一个动态规划问题。于是经过以下迭代方法即可确定最优的分期境界。
a.给定一分期境界底部水平, 求解上述动态浮锥法模型, 可获得一系列分期境界及其对应的采剥费用:
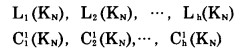
|
式中:KN—分期境界底部水平;
Li(KN)—底部水平为KN条件下第i个分期境界;
Ci1(KN)—分期境Li(KN)所对应的开采费用;
h—动态规划最末阶段所获得的分期境界个数。
b.用旋转式PV曲线计算不同分期境界条件下所对应的大境界扩帮部分的开采费用;
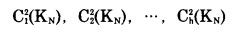
|
式中:Ci2(KN)—在分期境界底部水平为KN条件下分期境界Li(KN)所对应的大境界扩帮部分的生产总费用。
c.用标准PV曲线计算分期开采终了大境界剩余部分的生产总费用:C3(KN)。
d.计算在KN底部水平条件下, 各分期境界所对应的露天矿生产总费用:
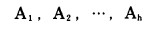
|
式中: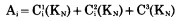
e.在KN底部水平下对应的最优分期境界为:
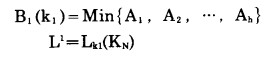
|
式中:B1(k1)—在KN底部水平条件下, 所有分期境界所对应的露天矿生产总费用中的最小者;
L1—最优分期境界, 这时对应的露天矿生产总费用为B1(k1), 底部水平在KN。
f.移动分期境界底部水平n次, 每次重复步骤(a)~(e), 即可求得在各底部水平条件下, 露天矿最优分期境界:
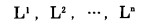
|
及对应的露天矿生产总费用:
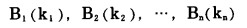
|
g.露天矿最优分期境界是所有露天矿开采总费用中最小者所对应的分期境界, 即
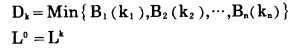
|
式中:Dk—在分期开采条件下, 露天矿开采最小总费用;
L0—露天矿最优的分期境界, 在该分期境界条件下, 露天矿开采总费用为Dk。
2 开拓运输系统优化设计开拓运输系统设计是露天矿分期开采工程设计中非常复杂而关键的环节。本文将CAD技术和优化技术结合起来, 较为完善地解决了这一问题。
2.1 开拓运输系统优化方法分期境界内开拓运输系统的确定, 实质上是一个多阶段决策问题。可以把时间作为阶段, 每个阶段内可能行走的路线作为状态。如何寻找一条或几条从堆矿点和排土场到最低开采水平的最优路径, 构成一个动态规划问题。
a.矿岩运输状态转移方程 露天矿生产从上到下逐水平进行, 这时不断有新的道路产生。每年生产的矿石量和岩石量, 除了走新形成的道路外, 还要走旧的道路才能运到堆矿点或排土场.因此, 矿岩运输状态转移方程为:
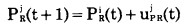
|
(8) |
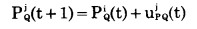
|
(9) |
式中:PRj(t+1)、PQj(t+1) —分别为从第一年初到第t+1年初已形成的第j条岩石和矿石运输道路;
uPRj(t)、uPQj(t)—分别为第t年内所形成的第j条新路段。
b.边界条件 矿石运输终点是堆矿点, 与之相连的场外道路是给定的; 岩石运输终点是排土场, 与之相连的场外道路也是给定的。因此有:
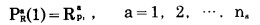
|
(10) |
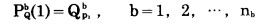
|
(11) |
式中:Rap1、Qbp1 —分别为第一年初所走的第a条排土路线和第b条运矿路线, 即固定的场外道路;
na、nb—分别为场外与排土场相连的排土路线条数和与堆矿点相连的运矿路线条数。
在开采终了时刻, 其运输路线起点为底部水平.由于范围小, 可选路线是可确定的.因此有:
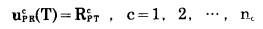
|
(12) |
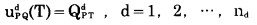
|
(13) |
式中:RPTc、QPTd—分别为第T年内所走的第c条新排土路段和第d条新运矿路段;
nc、nd—分别为底部水平岩石运输和矿石运输路段数;
T—分期开采服务年限。
c.约束条件 每年新路段的选择由露天矿空间位置决定。求解时必须确定每年新路段的选择范围。为此可以事先在境界最终平面图上设计可行的运输网, 然后用矿岩发展关系来圈定每年可能形成的运输路段。即
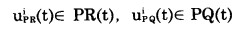
|
(14) |
式中:PR(t)、PQ(t)—分别为第t年内可能形成的新路段的集合。
d.目标函数 分期开采开拓运输系统的优化目标是希望所形成的运输网能使服务年限之内矿岩运输总费用达到最小。即
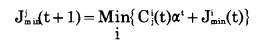
|
(15) |
式中:Jminj(t+1)—从第一年初到第t+1年初露天矿最小累计运输费用。这时第t年内所走的运输路线为第j条新路段, 且走第i条通达堆矿点与排土场的旧道路才把该年的矿岩运走;
Cji(t)—第t年内走第j条新路段, 且走第i条通达堆矿点与排土场的旧道路才把该年的矿岩运走所发生的运输费用。
式(8) ~(15)构成分期开采开拓运输系统动态优化模型。求解此模型就可确定最优的开拓运输网络。
2.2 开拓运输系统CAD设计方法用上述动态优化方法可以确定各水平的运输线路。于是, 开拓运输系统就可以方便地确定下来了。具体步骤如下:
a.运输网络连接 根据优化计算结果, 用直线初步连接各水平运输线路。这些直线基本上就是运输道路的中心线, 也同时确定了各水平出入沟的方向。
b.出入沟的设置 若某水平出入沟处台阶线是直线, 则此出入沟为直道出入沟; 若某水平出入沟处台阶线是曲线, 则先考虑用直道出入沟。若用直道出入沟可行, 则用它; 若不可行, 则用弯道出入沟。
c.区段外推 在开拓运输系线设计时, 经常要将某些水平一段区域内的一些工程线外推。如果用手工设计, 则将十分烦人; 如果用CAD技术, 则将十分简单。这一算法如下:
步骤一:用可旋转窗口捕捉某些水平内将要外推的区段; 用CAD捕捉命令捕捉区段内各水平要外推的工程线;
步骤二:用外推线生成命令外推区段内各水平的工程线; 将外推新线与其母线相连接并删除多余的母线;
步骤三:用CAD图形编辑命令进行整理。
d.局部修改 开拓运输系统网络连接完成后, 用CAD图形编辑命令对系统中不合理的地方进行必要的处理, 使整个系统达到工程设计要求。
2.3 通用图形库露天矿工程设计中常用的图形, 如台阶坡面线、台阶顶、底线、公路、铁路、出入沟、建筑物、常用标识等等, 这些常用图形在设计者给定一些条件之后, 就能在希望的位置上生成这些图。为设计方便起见, 本系统收集了大量露天矿常用的图形。各个图形由相应的控制程序引导, 由形象的图形菜单控制。一个图形激活后, 将按规范方式向设计者请求必要的支持。由于这一大型图库的强有力支持, 设计工作将十分方便, 效率和质量将大幅度地提高。
3 扩帮过渡优化设计露天矿分期开采扩帮过渡优化设计, 关键是要解决下列关键问题:
a.合理确定扩帮过渡开始时间;
b.合理分配小境界正常生产和大境界扩帮矿石开采量和岩石剥离量。
为了很好地解决上述问题, 本文提出了0-1混合整数规划方法, 从露天矿生产全局对分期开采扩帮过渡进行统筹优化。
3.1 基本原理露天矿生产是以一定工作帮坡角为基础进行的。如果露天矿以容许的最陡工作帮坡角进行生产, 那么由此而形成的矿岩采剥关系就称为临界矿岩采剥关系; 相反, 如果露天矿以容许的最缓工作帮坡角进行生产, 那么由此而形成的矿岩采剥关系就称为极限矿岩采剥关系。
a.小境界临界和极限矿岩采剥关系为:
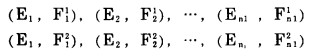
|
式中:(Ei, Fi1)、(Ei, Fi2)—分别为小境界临界和极限矿岩采剥关系第i个控制点, 其中Ei、为累计矿石采出量; Fi1和Fi2分别为累计临界和极限剥岩量;
n1—小境界临界和极限矿岩采剥关系控制点个数。
b.大境界扩帮临界和极限矿岩采剥关系为:
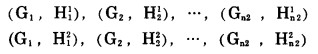
|
式中:(Gi, Hi1)、(Gi, Hi2)—分别为大境界扩帮临界和极限矿岩采剥关系第i个控制点, 其中Gi为累计矿石采出量; Hi1和Hi2分别为累计临界和极限剥岩量;
n2—大境界扩帮临界和极限矿岩采剥关系控制点个数。
露天矿扩帮过渡优化就是在小境界正常开采与大境界扩帮的临界和极限矿岩采剥关系之间寻求一个最优的矿岩采剥关系, 使露天矿生产处于最优状态。
3.2 优化模型扩帮过渡的最优采剥关系可用动态规划方法确定。但由于状态离散化的原因, 动态规划方法只能获得问题近似最优解.本文采用0-1混合整数规划可以获得问题的精确解。
a.目标函数 扩帮过渡优化设计的目标是露天矿生产总费用为最小。总费用包括小境界采剥总费用、大境界扩帮采剥总费用、设备购置费和设备闲置费。即
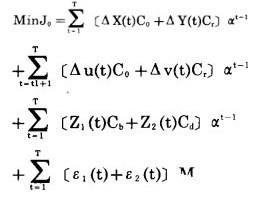
|
(16) |
式中:△—阶差分符号, △X(t)= X(t)-X(t-1);
X(t)、Y(t)—分别为从第一年到第t年小境界累计矿石采出量和累计岩石剥离量;
u(t)、v(t)—分别为从第一年到第t年大境界扩帮累计矿石采出量和累计岩石剥离量;
Z1(t)、Z2(t)—分别为第t年比第t-1年多采出矿岩量和少采出矿岩量;
ε1(t)、ε2(t) —分别为对应于Z1(t)、Z2(t)的误差;
C0、Cr、Cb、Cd —分别为单位矿石开采成本、单位岩石剥离成本、单位矿岩开采所需的设备购置成本和所付出的设备闲置成本;
t1—扩帮过渡开始时间;
M—相当大的正数。
b.约束条件 1°从第一年到第t1年, 露天矿在小境界内生产, 矿石年产量全部由小境界承担。即
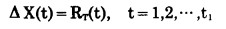
|
(17) |
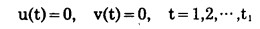
|
(18) |
2°从第t1+1年到第T年, 露天矿不但在小境界内进行生产, 而且在大境界内进行扩帮, 每年的矿石产量由这两个采场共同承担。即
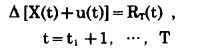
|
(19) |
3°每年小境界内累计岩石剥离量必须在其累计临界剥岩量和其累计极限剥岩量之间变化, 即
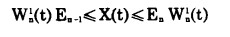
|
(20) |
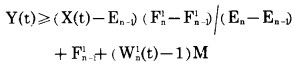
|
(21) |
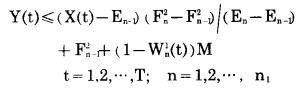
|
(22) |
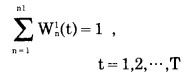
|
(23) |
式中:Wn1(t)= 0或1。
4°每年大境界扩帮累计岩石剥离量必须在其累计临界剥岩量和其累计极限剥岩量之间变化, 即
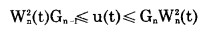
|
(24) |
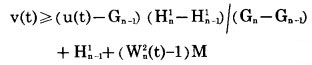
|
(25) |
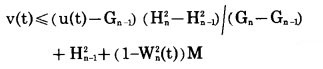
|
(26) |
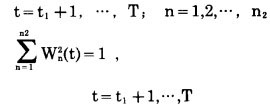
|
(27) |
式中:Wn2(t)= 0或1。
5°若第t年矿岩采剥总量比第t-1年矿岩采剥总量增加, 则将导致购买设备; 否则, 将导致设备闲置。即
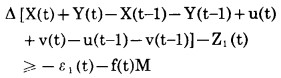
|
(28) |
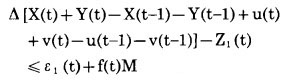
|
(29) |
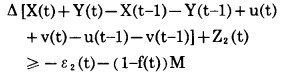
|
(30) |
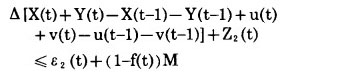
|
(31) |
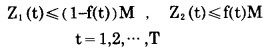
|
(32) |
式中:f(t) = 0或1。
6°开采终了时, 小境界和大境界扩帮范围内的矿岩量必须同时采完。即
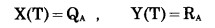
|
(33) |
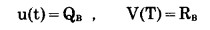
|
(34) |
式中:QA、RA—分别为小境界内矿石量和岩石量;
QB、RB—分别为大境界扩帮范围内矿石量和岩石量。
7°式(16) ~(34)中所有变量均非负。
3.3 问题求解式(16) ~(34)构成一个0-1混合整数规划模型, 可以用分枝定界法求解.该模型是在假定扩帮过渡开始时间为t1, 的条件下建立起来的, 求解该模型, 即可确定在该条件下的最优解.改变扩帮开始时间n次:
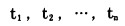
|
每次重新计算该模型, 就可获得各次的最优解:
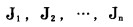
|
于是最优的扩帮过渡开始时间便可确定:
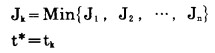
|
式中:Jk-n次计算得出的n个露天开采总费用中的最小者;
t*—最优扩帮过渡开始时间, 由第k次计算而得。
因此, 第k次计算所确定的小境界开采和大境界扩帮矿岩采剥关系为最优的矿岩采剥关系。
4 结论分期开采是露天矿较常采用的一种行之有效的采矿方法。该采矿方法特别适用于大型露天矿和深凹露天矿改扩建时矿床开采。这一点对我国许多老露天矿进行生产和技术改造以适应市场经济变化特别有用。本文应用优化技术和CAD技术, 提出了露天矿分期开采几个关键课题的动态优化模型。这对于分期开采优化设计无论是在理论上, 还是在实践上都有指导作用。
| [1] |
A.幻.德里任科. 深露天矿分期开采参数的论证[J].
国外金属矿采矿, 1988(12): 19–25.
|
| [2] |
张幼蒂, 杨荣新. 露天矿境界动态优化的探讨[J].
中国矿业大学学报, 1992, 3(3): 10–24.
|
| [3] |
西安冶金建筑学院, 等. 厂坝露天矿扩建工程的优化[J].
金属矿山, 1987(8): 23–26.
|
 1995, Vol. 9
1995, Vol. 9
