| 利用霍克-布朗破坏准则估算莫尔-库伦准则的摩擦角和粘聚力 |
2. 南方冶金学院教授
2. ${affiVo.addressStrEn}
霍克(Hoek)和布朗(Brown)[1~3]曾提出了一破坏准则*, 同时指出该准则中的材料常数m和s可经由布涅辛斯基(Bieniawski)的岩体评价值(RMR)[4]估算。由于该准则是少数利用工程地质数据有效地估计岩体强度的方法之一, 因此, 在岩石力学分析计算中已得到了广泛的应用。
*也即霍克-布朗准则, 译者注。
目前, 地下开挖工程的稳定性评价、边坡工程的分析计算, 大都使用莫尔-库伦(Mohr-Coulomb)破坏准则。因此, 用霍克-布朗准则所确定的强度曲线来确定莫尔-库伦准则中摩擦角φi″和粘聚力Ci′的当量值, 是经常要解决的问题。本文介绍该问题在下列三种情况下的求算方法:
a.已知有效正应力σn′, 这种情况一般适用于边坡稳定性分析中;
b.已知最小有效主应力σ3′, 这种情况适用于地下开挖空间的应力分析中;
c.单轴压缩强度在霍克-布朗准则和莫尔-库伦准则下相同, 也即, σcmasshb=σcmassmc, 这样的情况可在平均有效正应力σn′和最小有效主应力σ3′都未知的条件下应用。
在介绍上述三种情况下的求算方法前, 将重温一下基本的霍克-布朗准则、常数m和s与布涅辛斯基的RMR值之间的关系。
1 根据RMR值估计材料力学参数
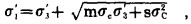
|
(1) |
式中:
σ1′——破坏时最大有效主应力;
σ3′——最小有效主应力或者侧限压力;
m, s——材料常数;
σc——完整岩块的单轴压缩强度。
应该指出的是, 此处完整岩块的单轴压缩强度指的是实验室用小尺寸试块(比如说, 直径50mm, 高100mm的试件)测得的强度, 试块中无节理、层理这样的不连续面。这样的强度值可度量岩石材料对岩体的整体强度的影响。
岩体的单轴压缩强度, 可以σ3′=0代入式(1)中得到:
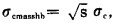
|
(2) |
类似地, 以σ1′=0代入式(1)中, 解此方程,可得到岩石或岩体的单轴拉伸强度:
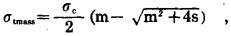
|
(3) |
为了把霍克-布朗准则与现场量测或观测值联系起来, 霍克和布朗总结了一系列岩体评价值RMR与常数m和s之间的关系式。RMR经由布涅辛斯基[4]的岩体分类法计算得到, 这些关系式, 经普雷斯特(Priest)和布朗的研究, [6]可以下列式子表示:
对受扰动的岩体,
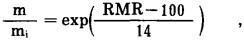
|
(4) |
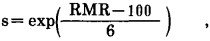
|
(5) |
对未受扰动的岩体或互相联锁的岩体,
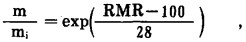
|
(6) |
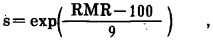
|
(7) |
式中, 对完整岩体, mi就是m, 、其由三轴试验确定[6]; 当无试验数据可资利用时, mi的值可参考附表估计。
| 附表 不同类型岩石mi的近似值 |
 |
| 点击放大 |
对于喜欢用巴顿(Barton)等人[7]提出的NGI岩体分类中的隧道质量指标Q的读者, 可用布涅辛斯基提出的下式[8]换算RMR的值:
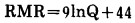
|
(8) |
根据霍克和布朗[3], 计算步骤如下:
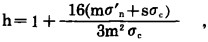
|
(9) |
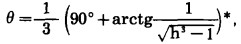
|
(10) |
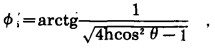
|
(11) |

|
(12) |
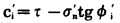
|
(13) |
岩体的单轴压缩强度, 利用上述计算得到的φi′和ci′, 可求得为:
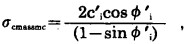
|
(14) |
岩体的单轴拉伸强度, 可按霍克-布朗准则经由(3)式计算得到, 该拉伸强度可作为按莫尔-库伦准则求算的单轴拉伸强度的下限。
3 已知σ3′求ci′、φi′、σcmassmc和σtmass若σ3′已知, 破坏时对应的σ1′可由式(1)计算得到, 其余有关量的计算如下:
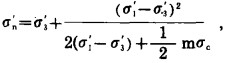
|
(15) |

|
(16) |
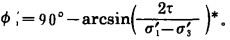
|
(17) |
*原文式中90°写成90, 特更正。
粘聚力ci′按式(13)计算, 岩体的单轴压缩强度和单轴拉伸强度分别按式(14)和式(3)计算得到。
4 莫尔-库伦准则和霍克-布朗准则下单轴压缩强度相同时, 求ci′和φi′岩体的单轴压缩强度, 在两准则下相同, 也即:σcmassmc=σcmasshb, 并且其值由(2)式计算, 其它有关值的计算如下:
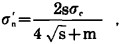
|
(18) |
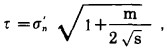
|
(19) |
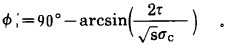
|
(20) |
粘聚力ci′按式(13)计算。
5 计算实例下面举例说明前述方法的应用, 并为读者提供一组值以检查自己的计算结果。
设有一种砂岩体, 其完整岩石材料的单轴压缩强度σc=60MPa, 查附表可得mi=15。根据巴顿等人提出的岩体分类法[7], 隧道质量指标Q为0.8, 按式(8), 相应的岩体质量评分值RMR=42。
现假定在该砂岩体中开挖有一边坡, 在靠近边坡的岩体内, 还开挖有其它的洞室空间, 因此, 可以认为, 由于边坡的开挖, 岩体中的应力降低了, 而且沿着岩体中的不连续面已产生了岩移。因此, 应该用受扰动情况下的式(4)和式(5)计算常数m和s。
根据式(4)和式(5), 可分别求得m=0.238和s=0.000063。把求得的m和s值代入式(2)和式(3), 可求得岩体的单轴压缩强度σcmasshb=0.476MPa, 岩体的单轴拉伸强度σtmass=-0.0159MPa。
5.1 已知有效正应力σn′的计算结果设有效正应力σn′=0.5MPa, 把其代入到式(9-13), 可得:
h=1.1927
θ=46.7174°,
φi′=41.896°,
τ=0.6610MPa,
ci′=0.2124MPa
对应于φi′=41.896°和ci′=0.2124MPa, 莫尔-库伦准则下的岩体单轴压缩强度, 按式(14)计算得, σcmassmc=0.9519MPa, 单轴拉伸强度, 按式(3)计算得, σtmssa=-0.0159MPa。
5.2 已知最小有效主应力σ3′的计算结果设最小有效主应力σ3′=0.25MPa, 对应破坏时的最大有效主应力值, 按式(1)求得为, σ1′=2.1958MPa*。
*原文中σi′误写为σi, 特更正。
把上述值代入式(15-17)中, 可求得: σn′=0.5940MPa**, τ=0.7429MPa, ,σi′=40.31°, ci′=0.239MPa。
**原文漏写单位MPa, 特补上。
对应于莫尔-库伦准则下的岩体单轴压缩强度, 按式(14)求得为, σcmaasmc=1.0322MPa, 岩体的单轴拉伸强度, 按式(3)求算为σtmass=-0.0159MPa
5.3 霍克-布朗准则和莫尔-库伦准则下, 岩体单轴压缩强度相同时的计算结果岩体的单轴压缩强度和岩体的单轴拉伸强度, 分别按式(2)和式(3)计算得, σcmasshb=σcmassmc=0.476MPa, σcmass=-0.0159MPa。
把完整岩块的单轴压缩强度σc=60MPa, m=0.238和s=0.000063代到式(18-20)中, 可求得:σn′=0.028MPa, τ=0.112MPa和φi′=61.94°, 按式(14), 相应可求得ci′=0.059MPa。
原载于英国《Int.J.Rock Mech.Min.Sci. & Geomech.Abstr.》Vol.27, No3, 227〜229, 1990
叶黔元 校
| [1] |
E.霍克, E.T布朗. 岩石地下开挖工程[J].
London, Instn.Min.Metall, 1980.
|
| [2] |
E. 霍克, E. T. 布朗. 岩体的经验强度准则. J. Geotech. Engng. Div. ASCE106, 1013-1035. 1980
|
| [3] |
E. 霍克, E. T. 布朗. 最新修正的霍克-布朗准则. Proc. 15th Can. Rock Mech. Symp., University of Toronto. 31-38. 1988
|
| [4] |
Z. T. 布涅辛斯基. 岩体的地质力学分类及其在巷道掘进中的应用. Proc. 3rd Congr. Int. Soc. Rock Mech., Denver, vol. 2, PartA, 27-32. 1974
|
| [5] |
E. 霍克. 第23届Rankine讲座. 节理岩体的强度. Geotechnique 33, 187-223. 1983
|
| [6] |
S. D. 普笛斯特, E. T. 布朗. 岩质边坡变滑面的概率稳定性分析. Trans. Instn. Min. Metall, 92. A1-A12. 1983
|
| [7] |
N. R. 巴顿, R. 廉恩, J. 伦德. 巷道支护设计中使用的岩体工程分类, Rock Mech. 6, 189-239, 1974
|
| [8] |
Z. T. 布涅辛斯基, 岩石工程中的岩体分类, 岩石工程研究(Z. T. 布涅辛斯基编)、Vol. 1. 97-106. Balkema, Rotterdam, 1976
|
 1992, Vol. 6
1992, Vol. 6
