| 浅谈萃取槽搅拌功率的公式推导与应用 |
在稀土溶剂萃取中, 搅拌机用得相当普遍, 几乎所的液一液两种物料的混合, 都离不开搅拌桨。搅拌桨所起的作用, 是向液相传递能量, 使两液相充分混合。要达到这个目的, 必须获取搅拌桨的输入功率的最佳数值。搅拌桨功率的计算正是为了确定两液相充分混合时理想的输入功率。
2 公式的推导和应用计算功率的公式可用力和速度来表示, 即
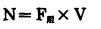
|
(1) |
式中: F阻为桨运动时所受的阻力。
V为桨运动时的线速度。
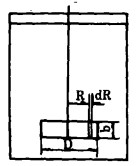
因此要计算桨的输入功率, 必须先求出F阻和V。我们以单叶片矩形搅拌桨为对象来分析桨的受力状况。如下图, 在距桨轴心R处取一长度为dR, 宽度为b的单元进行分析。若桨的转速为n, 混合液相的阻力系数为k, 比重为r, 则该单元的运动线速度为VR=2πRn, 其所受阻力方向和运动线速度方向相反, 阻力大小为
 |
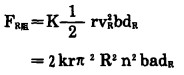
|
(2) |
该单元以VR速度运动时的驱动功率NR为:
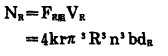
|
则桨以转速n旋转时的驱动功率N为:
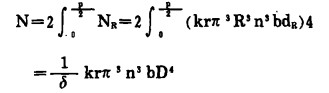
|
(3) |
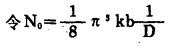
|
(4) |
则桨的驭动功率公式为:
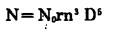
|
(5) |
在(4)式中的N0被学界称作功率准数, 它是与多种因素有关无因次数群, 可通过实验求得, 但较复杂.此外桨的尺寸参数与萃取槽高宽比间有一定的比例关系, 当萃取槽高宽比确定后, 桨的尺寸即可确定。由于稀土的溶剂萃取所用萃取槽的高宽比常介于1~1.15之间, 对应于每一个高宽比和不同桨型, 都有一个功率准数与之对应.因此都得先求出其功率准数方能计算出桨的驱动功率, 就使得桨的功率计算变得更加烦锁。清华大学化工系的李洲等通过实验得出了各种型式搅拌桨在方形萃取槽(高宽比为1)中功率准数, 如下表。
| 附表 各式桨在方形槽内的搅拌功率准数 |
 |
| 点击放大 |
对于高宽比介于l~1.15之间的萃取槽, 我们可以先假定其高宽比近似地等于1、利用搅拌桨在方型(高宽比为1)萃取槽内的功率准数求出方形槽的桨驱动功率N方, 然后根据混合液相单位体积输入功率相等的原则, 由N方求出实际萃取入功率相等的的搅抖桨的驱动功率.以此可大大地简化功率计算手续。下面以卖解说明功率的简化计算方法:
例某稀土分离厂用10级/架, 每级混合室容积为50l的混合澄清萃取槽, 搅拌桨转速n=6.15rpm, 现场测得混合室中混合液相的比重介于1.05~1.10g/cm3间, 求搅拌桨的驱动功率并选择电机。
解: 50l混合室尺寸取3.6×3.6×4(l), 高宽比为1.11。主搅拌桨为半封闭直叶式泵式桨, 桨叶外径D1 = 150mm, 桨叶宽度b1=60 mm, D1 /b1= 2.5, 由上表和(4)及(s)得: D/b=2.5的桨驱动功率是D/b=5的桨驱动功率的两倍。付桨为双叶平桨, 桨叶外径D2=85mm, 桨叶宽度b2=4mm, D2/b2=2, 由上表及(4)和(5)得:D/b= 2的桨驱动功率是D/b=4的桨驱动功率的两倍
a 先求出方形萃取槽(3.6×3.6×3.6l)的桨驱动功率N方由上表知: N01 = 2.6, N02= 2.3。
N方=2(N01D15 n3r+N02D25n3r)
=2×(50.5+2.6)=106(w)
b 求混合液相的单位体积输入功率Nv
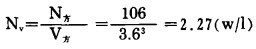
|
c 求实际混合室3.6×3.6×4(l)搅拌桨的驱动功率N搅
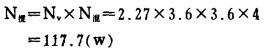
|
d 选择电机
由于是电机驱动皮带轮带动桨运动的, 因而必须考虑电机及皮带传动的效率。由资料查得:三角皮带传动效率η1=0.95, 平皮带传动的效率η2=0.97, 滚动轴承座的效率叮η3=0.99, 电机效率η4=0.7~ 0.9, 取η3=0.8, 则总效率为:
η=η1•η2•η3•η4=0.73
则电机所驱动的功率N为:
N = N搅×混合室级数÷η
=117.7×10÷0.73=1612(w)
电机的负载功率N电=KN(K为过载系数, K取值l~1.3, 取K=1.2)
N电 = K·N =1.2×1612=1934(w)
由电机目录取额定功率为2.2kw的电机。
计算结果与实际选择是基本符合的。
3 结语a 利用一定的手段, 我们借助方形萃取槽的搅拌功率准数来计算非方形萃取槽(高宽比不等于1)的桨驱动功率, 简化了桨功率的计算, 计算结果与实际也比较接近。
b 利用上述方法求出的功率是近似值。高宽比越接近1, 所计算的功率与实际间误差越小, 反之误差大。对高宽比小于1.15的稀土萃取槽用上述方法是比较适合的。
| [1] |
L.M.米尔-恩汤姆森.
理论流体力学[M]. 北京: 机械工业出版社, 1984.
|
| [2] |
 1992, Vol. 6
1992, Vol. 6
