| 企业自备电厂柴油发电机组的运行优化 |
盘古山自备电厂是钨业系统较大的自备电厂, 现有柴油发电机组8台, 装机容量3500kw。近年来, 外部供电严重不足,自备电厂起着补充电量、调荷顶峰重要作用, 为缓解电力供需矛盾、保障生产生活正常进行, 做出了贡献。该矿发电量一般为(700-800)×104kwh(最高年份为1380×104kwh, 占当年总用电量的70%以上)。在发电机输出电能的同时, 柴油机吞噬着大量的柴油, 企业年发电用柴油量约2000吨(最高年份为3435吨)。多年来, 在加强管理、精心操作、精心维护上做了大量的工作, 在保证安全供电、降低油耗方面取得了一定的成绩。但仍然停留在以满足用电需要为目的, 以电量、功率平衡为准则的运行管理状况还未臻完善。在传统管理中,对发电机组的经济运行, 除提高效率外, 如何科学地组合电源、合理分配负荷, 才能实现最大限度的燃油节约,尚未引起应有的重视。当前, 对并列运行机组分配负荷的原则一般是:(1)按机组的效率分配负荷, 即油耗低、效率高的带满负荷, 油耗高、效率低的机组少带负荷; (2)按机组的经济负荷或者简单地按机组额定容量以固定分配系数进行分配, 这是不符合经济分配原则的。进一步降耗节油还大有文章可做。
电力在生产、传输和分配时的损耗绝对值相当可观,不同程度地潜在着节约的可能。而潜能的发掘和利用, 必须依靠技术进步和现代化管理手段。因此, "OPt"(最优化)作为现代控制理论和方法, 如同"TQC"一样, 必将在我们探索现代化管理的进程中, 受到愈来愈多的重视。"最优化"就是使问题的解决在一定程度上达到无可争议的完善化。电厂的经济运行也称经济调度, 其数学处理方法就是属于工程系统分析最优化问题或称最优规划问题。其目的是在保证整个系统安全可靠和电能质量的前提下, 合理地组合电源和分配负荷, 使电能生产的费用最小, 获得最大的经济效益。
2 运行最优化的技术基础最优化技术工作是以数学最优化理论为基础的。在讨论最优控制时, 必须首先把实际的工程技术问题抽象成数学问题来考虑。数学模型一般由运行变量、约束条件和目标函数组成。柴油发电机组应以机组为研究对象, 以满足用电需要为前提。所以, 为开展优化工作, 首先必须掌握需用负荷及机组耗量特性。
2.1 目标函数选择及机组耗量特性为了从众多的"容许控制"集合中遴选出"最优控制"方案, 就需要有一个判据, 一个衡量控制作用孰好孰坏的"性能指标", 即所谓"目标函数"。自备电厂最优控制应以降低发电成本为最终目的。柴油发电厂的生产费用包括燃油、厂用电、备件材料、设备折旧、工资、管理费用等等。在这些费用中唯有燃料费用在总成本中占有较大比例(约85%), 且与电能生产存在着直接的关系。因此, 柴油发电厂的经济运行问题实质上就是最小燃料控制问题, 这里的目标函数应是燃油耗量的函数。
柴油发电机组的耗油量和许多因素有关, 诸如爆发压力、喷油时间、水温、油温等, 但主要是和发电机输出功率关系最为密切。函数关系Qz=f(PGi)称为机组的耗量特性, 用以作为最优控制的目标函数, 而将对运行指标影响最大的基本参数——有功功率PGi作为控制变量。耗量特性曲线可从厂家提供的技术资料中获得, 也可通过实测数据绘制而成。现将耗量特性以数学解析式(2-1)表达:
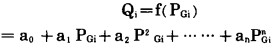
|
(2-1) |
对于每一个取定的功率值PGi, 就有一个确定的燃油量值Qi与之对应, 选取曲线中一些特征试验点, 就可以列出一些以待定系数a0、a1、a2、……an为未知数的一次方程:
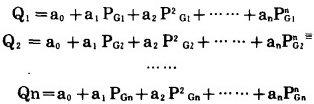
|
通过求解以1、PGi、P2Gi……PGin、Q1所构成行列式, 可得特性方程中各系数的一组唯一确定的解:
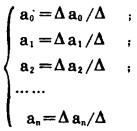
|
显然, 耗量特性解析式的准确性与选取计算点的数量有关。计算点取得越多,准确程度就越高, 但是待定系数的维数和所得耗量特性方程中的次数都成比例地增高,这将给计算工作带来很大的困难。因此,除微机外, 一般以选取3~4个点为宜。
至此, 可求得图 1中《6300ZD柴油发电机组》的耗量特性曲线的解析式为
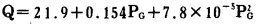
|
(2-2) |
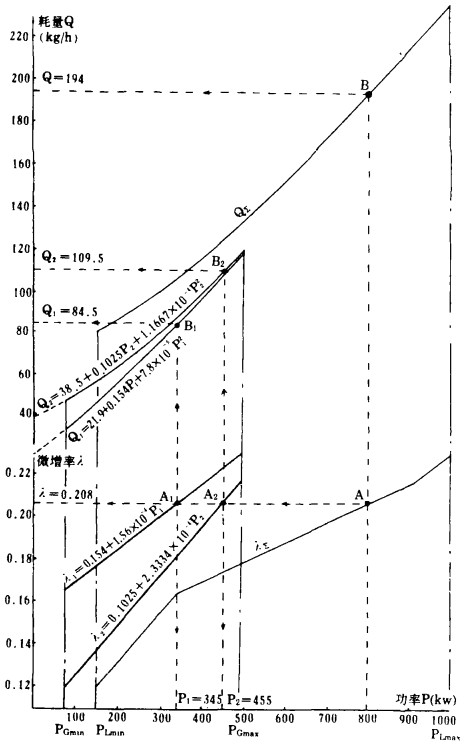 |
| 图 1 图解法求负荷最优分配 |
而耗量微增率特性为:
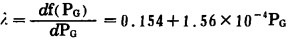
|
(2-3) |
上式反映了《6300ZD柴油发电机组》在受控动态过程中, 燃油耗量及其微增率与输出有功功率之间的关系, 并作为该机运行优化的"目标函数"。
2.2 等约束条件及负荷曲线为使优化方案具备经济上的合理性和技术上的可行性, 应根据系统对电能在数量、质量和安全诸方面的要求, 对有关控制变量的取值范围加以限制, 以构成优化控制中的"约束条件"。电力系统是发、供、用电紧密联系的统一体, 电能既不能大量储存又不可须臾中断, 产、供、销必须同时进行。要求发电和用电双方有功功率随时保持动态平衡, 是电力系统正常运行的首要条件。也是优化控制的前提。
就某个系统而言, 在不计及网络损耗时, 应满足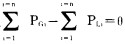
式中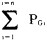
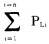
我们将上式表达的"有功功率必须保持平衡的条件"称之为"等约束条件"。表示为
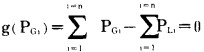
|
(2-4) |
最优方案应以满足负荷需要为前提, 因此必须首先掌握需用负荷情况。企业用电负荷在一定生产方式下是周期变化的。它可以分解为几种有规律可循的变化分量。其中周期较短、幅度较小的"随机分量"和"脉动分量", 一般可由调频、调速器的调差特性来部分或全部吸收; 而由于生产、生活、气象等变化引起的"基本负荷分量", 就必须由系统中运行的发电机组来供给。这部分负荷分量幅度较大, 周期较长, 具有持续性和规律性, 可以预测, 并用"有功功率日负荷曲线"来描述。它是应用累积的运行记录, 结合科学的统计分析方法加工绘制的。
曲线PZ为企业总负荷(kw); Pw为外部电网向企业供电的负荷(kw), 是根据上级计划分配的日用电量和许用负荷来编制。这时应重点考虑电网的限峰负荷。电网峰荷时少用, 谷荷时多用。
PN为自供电负荷, PN=PZ-PW(kw); 这就是企业自备电厂柴油发电机组应带的用电总负荷或称总出力(也即PN=∑PL), 并构成机组优化运行的等约束条件。编制PN曲线时应着重考虑电厂总出力的下限和上限。另外, 从保证电能质量和安全角度出发, 还必须对机组有关运行参数的取值划定一个容许范围, 称为"不等约束条件"分别为各机组有功功率PGi、无功功率QGi和输出电压Ui所不得逾越的限额, 作为运行优化的边界条件。限于篇幅, 本文不拟作进一步论述。
2.3 运行控制的寻优方法及负荷分配当目标函数和约束条件业已确定, 柴油发电机组运行优化问题被抽象为数学问题后, 根据塑模的类型和特点; 可知行将解决的是等约束条件下多变量函数寻优问题。为了把约束优化转化为无约束优化问题。采用拉格朗日(Lagrangian)乘子法, 根据已知目标函数f(PGi)和等约束条件g(PGi)建立一个新的、不受约束的目标函数即拉格朗日函数
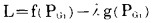
|
(2-5) |
式中λ为拉格朗日乘子。
为简化初步分析, 将问题局限在两台机组之间, 并略去网络损耗。拉格朗日函数为
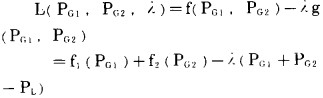
|
(2-6) |
这样, 最小燃料问题转化成求函数最小值。其条件为
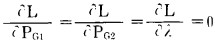
|
也就是
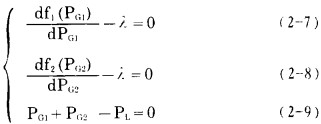
|
其中(2-9)式就是给定的等约束条件即功率平衡条件。而(2-7)、(2-8)式的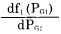
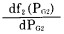
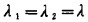
|
(2-10) |
上式表明, 各机组的耗量特性f(PGi)对各自出力PGi的导数(即耗量微增率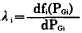
从物理意义上解释为:并列运行机组间应合理分配负荷, 使得耗量特性不尽相同的各机组都按相等的耗量微增率运行,才能获得最大的节约。如若不然, 即应进行负荷调整。调整的原则是降低高微增率机组的负荷,同时等量增加低微增率机组的负荷, 在保持总功率不变的情况下,使总燃油耗量减少。调整过程中的油耗对比可通过下列计算来说明:
机组油耗量Qi=Qoi+λiPGi等式后第一项是空载耗量, 其值不随负荷而变化; 第二项则是随负荷变化的有功耗量。调整前机组Ⅰ、Ⅱ的负荷和微增率分别为Pi、(PL-P1)和λ1、λ2(且设λ1>λ2),这时两机组总耗量为
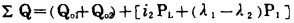
|
负荷调整时, 将机组Ⅰ的负荷减少ΔP(P'1= P1-ΔP); 机组Ⅱ等量增加ΔP(P'2=PL-P1+ΔP)。此时燃油总耗量为
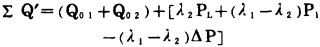
|
调整前后比较, 两种运动方式总耗量之差为
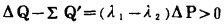
|
而且只要两台机组耗量微增率存在差值, 从高微增率机组(机组Ⅰ)向低微增率机组(机组Ⅱ)转移负荷的调整就总是有利的(ΔQ>0)。如果将这种改变负荷分配的过程继续下去, 可使总耗量渐次减少, 直至λ1=λ2时为止。这时, 两台机组总耗量最小,处于最佳运行状态。这就是满足功率平衡条件下, 求得总耗油量最小所必须遵循的"等微增率准则"。
无疑,上述分析方法和导出的结论可推广运用于多台发电机组之间的负荷分配。只是这时, 式(2-6)应改写为
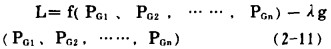
|
(2-11) |
式(2-10)应改写为
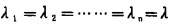
|
(2-12) |
a.分别作出机组Ⅰ和机组Ⅱ在PGimin~Pimax区间耗量特性曲线Q1、Q2以及微增率曲线λ1、λ2; 并绘制综合耗量特性曲线Q∑和综合微增率曲线λ∑, 作为调度曲线。
b.由等约束条件PG∑(t)=PL(t), (从日负荷曲线查得), 对于每个给定的总负荷PL(设800kw), 可以向上在λ∑曲线和Q∑曲线上找出对应点A、B。Q(B)=194kg/h、λ(A)= 0.208则为两机组总出力PG∑=800kw时的总耗油量和综合微增率。
c.据"等微增率准则", λ1(A)=λ2(A)=λ∑(A)可由A点水平面向左在λ1、λ2曲线上分别找出A1、A2点。
d.由A1、A2点竖直向下,在功率轴上找出P1、P2点, 其对应的读数P1=345kw、P2=455kw,即为机组Ⅰ、机组Ⅱ按"等微增率准则"分配应带的负荷。校验等约束条件是否成立。
e.由A1、A2点竖直向上, 在Q1、Q2曲线上得B1、B2点, 并分别水平向左在耗量轴上得出Q1=84.5kg/h、Q2=109.5kg/h,即为机组Ⅰ、机组Ⅱ在各自出力情况下的小时耗油量。同样, Q1+Q2应与B点对应的Q∑相符,即
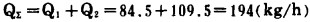
|
在已知机组耗量特性解析式时,可以用拉格朗日乘子法求解。
两台共同供电的机组耗量特性分别为:
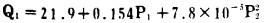
|
(3-1) |
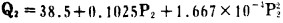
|
(3-2) |
求供电总负荷PL=800kw时负荷最优分配方案及耗油量。步骤如下:
a.建立拉格朗日函数
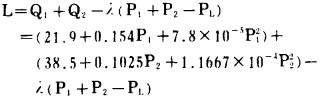
|
b.上述函数取导数, 得极值条件为:
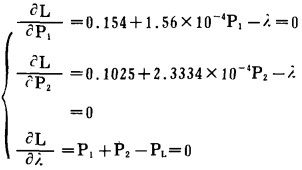
|
c.解方程组得
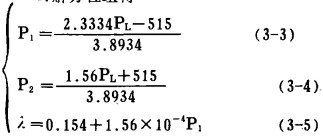
|
(或λ=0.1025+2.3334×10-4P2)
将PL=800kw代入, 得
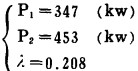
|
d.将上述结果代入(3-1)和(3-2)式, 得机组耗油量Q1、Q2和总耗量Q∑
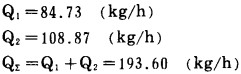
|
可见, 图解法和拉格朗日乘子法求解等约束条件下多变量函数寻优, 结果相同。
3.3 运行机组有功负荷的最优分配方案已知PG1min=PG2min=75kw, PLmin=150kw; PG1max=PG2max=500kw, PLmax=1000kw。
a.当PL=150kw时, 受不等约束条件限制, 两台机组都按下限功率发电, 各承担75kw, 这时λ1=0.1657, λ2=0.1200
b.150kw<PL≤345kw阶段,因为λ2<λ1, 增加负荷时,应首先在低微增率的机组Ⅱ上增荷, 机组Ⅰ仍按下限发电, 这时综合微增率取决于机组Ⅱ。直至λ2=λ1= 0.1617(此时PG2=270kw, PL=PG1+PG2=345kw), 机组间才真正开始按"等微增率准则"分配负荷。
c.345kw<PL≤917kw阶段, 按"等微增率准则"分配负荷, 取不同的PL值代入(3 -3)—(3-5)式, 即可求得各种负荷情况下的PG1、PG2和相应的λ值。当PL=917kw, λ1=λ2=0.2192时, 机组Ⅱ首先达到上限功率(PG2=500kw)。
d.917kw<PL≤1000kw阶段,机组Ⅱ受不等约束条件限制, 不能再增带负荷, 仍按上限发电; 增加负荷只能在机组Ⅰ上进行, 此时综合微增率决定于机组Ⅰ。
当PL=1000kw时, 机组Ⅰ也达上限功率, 两机组并列系统处于最高出力状态运行。
| 表 1 最优分配方案(kw) |
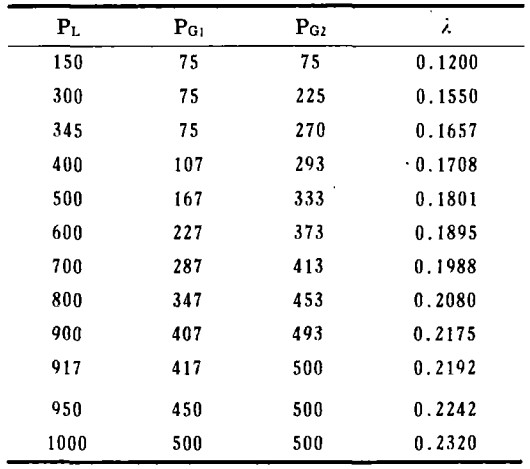 |
| 点击放大 |
4 结语
a.提高柴油发电机组运行的经济性, 对节能降耗, 提高经济效益有重要的意义。
b.本文简述的机组间负荷最优分配的"等微增率准则", 可作为电厂经济调度的基本原则。
c.最优化技术为电厂的经济运行展现了广阔的前景。在目前条件下, 为使最优化技术在实践中发挥有效作用, 还需做好以下工作:
一是在对累积运行记录和测试数据进行统计分析的基础上, 开展企业用电负荷预测, 绘制各种生产方式下有代表性的预计负荷曲线, 作为运行优化的前提; 二是企业现有柴油发电机组大都缺乏耗量特性资料, 就是新增机组, 由于安装、使用条件有异, 其实际耗量特性与出厂试验数据也不尽相同。因此, 必须通过能量平衡测试, 掌握机组输出功率与消耗油量之间的数量关系, 进而求出全厂综合耗量特性和微增特性, 作为经济调度的依据; 三是运行优化是以数学最优化理论为基础的, 应用电子计算机自动寻优, 是加速企业电力系统运行最优化进程的有效途径。
 1992, Vol. 6
1992, Vol. 6
