| 一个简单实用的应变软化模型 |
应变软化是岩石进入后期强度阶段时的渐进破坏现象,同时也是岩石的一个不可忽视的固有特性。在岩体工程稳定性分析中,是否考虑岩石的应变软化特性,所得计算结果与实际工程结构力学行为的逼近程度是不同的,有时还可能导致截然不同的稳定性评价结果。此外,由于岩石的失稳破坏一般说来是应变软化的结果,故只有更深入地研究岩石的应变软化特性,并建立起考虑了这种特性的岩石破坏准则,才能更好地解决岩体工程稳定性评判问题。
几十年来,不少学者进行了有关岩土体应变软化特性的研究并提出了一些用来描述软化规律的力学和数学模型。虽然这些模型繁简各异,但都在一定程度上反映了土体或岩体的应变软化特征。其中值得指出的是文献〔1〕、〔3〕中所描述的软化模型,虽然缺乏关于软化机理的较深入的探讨,但模型简单,待定参数少,实用性较强。本文则试图在综合上述软化模型的基础上,进行一些改进和补充,以完善软化模型理论。
一 岩石的弹塑性软化本构关系从许多实验结果来看,岩石的硬化或软化过程伴随着明显的塑性体积改变,尤其是在岩石破坏前的软化阶段,由于微裂隙的迅速增长,即使在相当大的围压和致密的岩石情况下,也确实出现体积膨胀或称扩容的现象〔2〕。因此,将岩石材料的塑性参数取为塑性体积应变增量的函数,也可望在一定程度上反映出岩石的软化特性。
根据弹塑性力学理论,塑性条件一般可表示为:
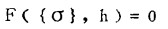
|
(1) |
式中:{σ}为应力状态;h为材枓的塑性性态参数。本文假定h为塑性体积应变增量的函数,即
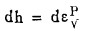
|
(2) |
此外,塑性力学中通常假定塑性应变增量的方向为某一塑性势G=G({σ},h)的梯度方向,亦即
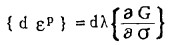
|
(3) |
其中,dλ>0为一比例系数, εp为塑性应变分量。由此可将全应变增量表示为:
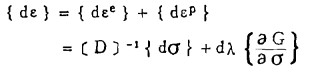
|
(4) |
对塑性条件式(1)微分,则有
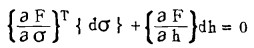
|
(5) |
由(2)、(3)及关系式εvp=ε1p+ε2p+ε3p可得
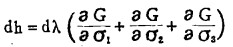
|
(6) |
将(6)代入(5), 并令
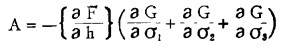
|
(7) |
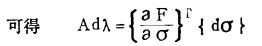
|
(8) |
将式(4)两边同乘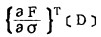
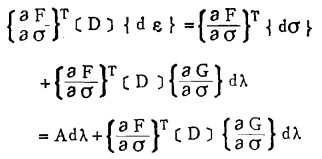
|
整理, 得
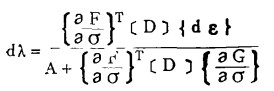
|
(9) |
又由(4)式可得
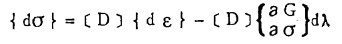
|
(10) |
将(9)代入(10), 可得
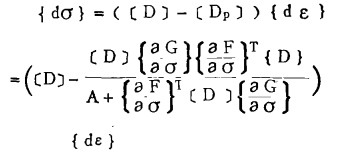
|
(11) |
其中A>0对应于应变硬化, A<0对应于应变软化, A=0即为理想塑性情况。
二 岩石的应变软化规律考虑到一般岩石的残余摩擦角与其达峰值强度时的摩擦角相差不多,为简化起见,可假定岩石发生软化前后的摩擦角不变,即岩石为等向软化或等向硬化,而岩石的粘结力C则按下式的指数函数式变化
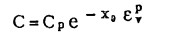
|
(12) |
式中:Cp为岩石的峰值粘结力:εvp为岩石的塑性体积应变; x0为试验常数。X0可通过几组不同侧压三轴压缩试验的完整应力应变曲线,借助于回归或拟合方法确定之。
当然,式(12)也可假定成摩擦角α与粘结力C的联合变化式,以考虑二者所共所产生的强度软化影响,但两种情况下的软化计算原理是相同的。
如果将塑性条件式(1)取为莫尔一库伦型屈服面方程
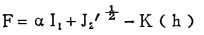
|
(13) |
且令G=F即采用相关的流动法则以及将塑性性态参数直接取为塑性体积应变由εvp,由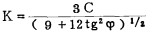
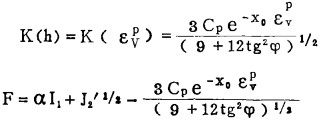
|
(14) |
对上式进行微分,即可得式(7)中的
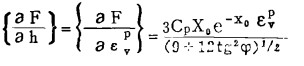
|
至此,由式(11)所表示的本构关系式就基本确定下来了。
在上述应变软化模型的实际应用中,塑性体积应变εvp的确定是至关重要的,本文建议了如下的计算方法。
根据塑性位势理论,与塑性条件(13)相关连的流动法则应为:
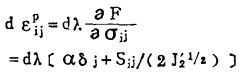
|
式中:εijp为塑性应变张量,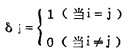
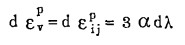
|
将式(9)代入上式,有
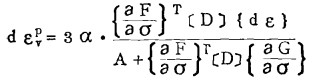
|
(15) |
这样,在采用有限单元法进行应力计算时,不同时刻和应力状态下的εvp值就可通过式(15)在计算过程中累加得出,从而借助于一个适当的有限元迭代过程即可实现基于上述软化模型的应力分析计算了。
三 算例在岩体中开掘一圆形巷道,如图 1所示。外边界荷载条件为:水平构造应力从上到下按线性规律变化,最小和最大值分别为6和llMPa; 竖向压应力为均布荷载,其值为2Mpa。岩体的力学参数为:E=5.4×103MPa, μ= 0.2, Cp=2MPa, φ=38°, γ=3000kg/m3,x0=200。为便于对照比较,分别进行了线弹性、理想弹塑性及软化弹塑性三种分析。
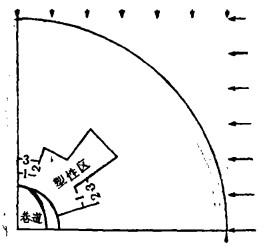 |
| 图 1 三种不同力学计算模型下的巷道周边位移及塑性区分布图 |
图 1中给出了三种不同情况下的巷道周边位移曲线及塑性区分布图。图中的数字1、2、3分别对应线弹性、理想弹塑性及软化弹塑性的计算结果。从图中可以看出,考虑了岩石强度软化后的巷道周边位移和塑性区域都是最大的,理想塑性者次之,而线弹性情况下的位移和塑性区最小。考虑强度软化时的巷道围岩中的塑性区域要比理想塑性情况下的塑性区面积高出8.3%。
图 2中给出了三种情况下的巷道周向应力沿径向的变化曲线。从图中亦可看出,在靠近巷道周边2倍半径范围之内,亦即图 1中所示塑性区内,由考虑软化特性所得出的巷道周向应力最小,对应着所谓的应力松驰区;而在接近2.5~3.5倍巷道半径范围内,为考虑软化特性情况下的应力升高区,其周边应力值则高于理想塑性甚至线弹性情况下的相应值;超过3.5倍巷道半径的范围之外,三种情况下的应力值则基本趋于一致。
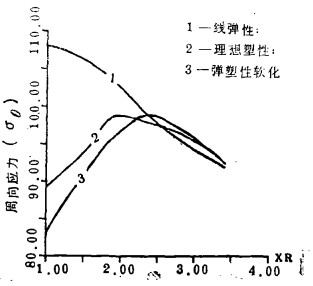 |
| 图 2 三种不同力学计苏妞里下巷道周向应力沿径向的变化曲线图 |
由以上计算结果可知,考虑了岩石强度软化后的工程岩体的稳定性将会有所降低,但这将更符合实际岩体的真实状况。因此,对于较重要的岩体工程结构,有必要进行岩体软化弹塑性稳定性分析,以提高应力分析结果的可靠性。本文所描述的软化弹塑性模型能在一定程度上反映岩石的软化特性,是基本正确的,可用来作为选择弹塑性软化模型时的参考。
| [1] |
于学馥, 刘怀恒等著, 地下工程围岩稳定性原理煤炭工业出版社, 1983
|
| [2] |
王仁.
塑性力学基础[M]. 科学出版社, 1982.
|
| [3] |
杨 更社, 刘 怀恒. 应变软(硬)化有限元分析及应用[J].
第一届全国计算岩土力学研讨会论文集, 1987, 11. |
 1991, Vol. 6
1991, Vol. 6
