| 矿石贫化率计算式的评价和分析 |
矿石贫化率如同矿石损失率一样,是矿山企业的一个重要工业指标。其计算法的合理性直接影响到矿山企业经济效益计算和采矿法或资源利用程度评价的正确性。近十年来,有关贫化率计算问题的文章较多,大多各持其说,莫衷一是。对此,颇感有必要进一步讨论,对贫化率计算式进行评价和分析。
一 对现有的贫化率计算式的评价我国采矿界现在采用的矿石贫化率计算式有不少,但归纳起来主要有两类:
第一类是矿业院校旧教科书中的传统计算式〔1〕,它根据围岩是否含有用成份而分成矿石视在贫化率和实际贫化率。
视在贫化率(ρ)是工业矿石品位(α)与采出矿石品位(α′)之差对工业矿石品位(α)之比,即
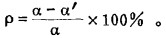
|
(1) |
实际贫化率(ρ′)是混入采出矿石中的废石量(R)对采出矿石量(T)之比,即
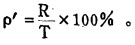
|
此为直接式,其R不能直接测得,于是通过联立方程
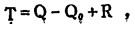
|
(2) |
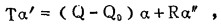
|
(3) |
得到与直接式相等的间接式
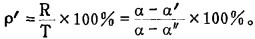
|
(4) |
式(2)、(3)中,Q、Q0分别为工业矿石量和工业矿石开采损失量,α″为废石品位,其它符号同上。
第二类是矿业院校新教科书中的计算式〔2〕,它根据围岩是否含有用成份而分成矿石贫化率和废石混入率。
矿石贫化率(ρ)就是前类的视在贫化率,其计算式也为
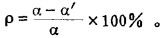
|
(5) |
废石混入率(γ)就是前类的实际贫化率,其计算式也为
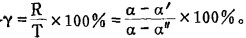
|
(6) |
这两类计算式虽然都在广泛应用,尤其是第一类至今还是矿山设计和损失贫化统计工作中的最基本的计算式,但都还不够完善,还存在如下两个问题:
1.没有把视在贫化率看成也是一种矿石实际贫化率。(1)、(4)式来自苏联,其中(1)式的“视在”是俄文“ВИДИМОЕ”的翻译词,其意是“看得见的、形表的”,进而被引伸为“非实质(际)的”。按此意,(1)式计算出来的贫化率自然就是没有考虑混入废石影响(α″=0)的非实际贫化率了。若仅就数学而论,(1)式确实不反映实际贫化率,但从采矿而论,则反映了实际贫化率。因为采出矿石中包括了混入的不含矿废石,而α′又是来自采出矿石的取样化验资料。因此,(1)式应是代表围岩不含矿情况下的采出矿石的实际贫化率。
2.没有把废石混入率看成也是一种矿石贫化率。作为废石混入率的计算式(6),其实就是实际贫化率的计算式(4),当然也是苏联和美国的贫化率计算式。贫化率的俄文、英文单词分别是“Разубожияание”、“dilution”,其基本含义是“贫变、贫度、冲淡、淡度”,在化学中贫(淡)度的通俗说法是无用物对有用物或混杂物(有用物加无用物)之比,它同有用物对无用物或混杂物之比的浓(稠)度的通俗说法恰成互倒或互补的关系。对于采矿,贫变或冲淡是一种废石化作用,贫(淡)度应是反映废石相对含量的废石度或反映废石化的相对程度。因此,按化学概念说废石混入率实际上就是矿石贫化率,两者是一回事。这也可用数学方法佐证,如令α″=0,并联立(2)、(3)方程式,便得
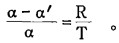
|
(7) |
(7)式左边就是(1)式的视在贫化率或(5)式的矿石贫化率,右边就是(6)式的废石混入率。因此,矿石贫化率等于废石混入率。
这里顺便说明两点:1.严格说废石混入率与矿石贫化率不等,但考虑到造成矿石贫化的主要原因是大量废石混入,至于少量的富矿粉丢失或有用成份淅出和很少出现的富矿柱弃采等均为次要原因,几乎可忽略不计,因此两者可取近似相等。2.(5)、(6)式虽然都是代表矿石贫化率,但前者是适用于围岩无品位的,后者是有品位的。两式中的α、α′值是不同的。有的文章举了这样的例子,如α=60%Fe,α′=50%Fe,α″=0,代入(5)式得贫化率ρ=16.6%;α=60%Fe,α′=50%Fe,α″=25%Fe,代入(6)式得贫化率γ=28.6%。于是认为,既然会出现围岩有品位时的贫化率大于无品位时的贫化率的这种奇怪现象,那说明(6)式不能代表矿石贫化率,而应代表废石混入率。显然,这例子是不对的。因为,上述这两式代表不同的情况,其参数值当然不同,即使α相同,α′也不能相同。在α″=0情况下,若α=60%Fe,α′=50%Fe,则在α″=25%Fe情况下,应取α≤60%Fe,α′>50%Fe(因在两种情况中,废石混入量和取样化验技术相同条件下,由于废石品位较高,所以出矿品位应提高才符合采矿技术逻辑)。
鉴于存在上述两个问题,为了进一步统一和简化贫化理论,笔者认为,矿石贫化率的正确定义应是:矿石被废石化的相对程度或矿石中废石的相对含量称为矿石贫化率。根据这定义,建议视不同情况采用如下四个贫化率计算式:
当废石品位α″=0时,
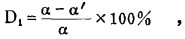
|
(8) |
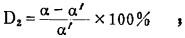
|
(9) |
当废石品位α″ 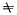

|
(10) |
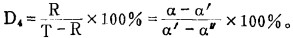
|
(11) |
式中:D1、D2、D3、D4 —矿石贫化率(%);
α、α′、α″—工业矿石、采出矿石和围岩的品位(%);
T、R—采出矿石量、混入围岩量(吨)。
这四式具体应用时,须注意其不同的适用性。
二 对建议的贫化率计算式适用条件的分析式(8)、(9)、(10)、(11)的适用性可用赞比亚采矿工程师E·A·Wright所提出的贫化率精确度和灵敏度计算原理〔3〕进行分析。该原理数学推导有误,下面在分析中做了相应修改并结合具体公式做了一定的发挥和探索。
(一) 围岩不含矿计算式的精确度和灵敏度分析1.精确度分析。假设D1*、D2*为矿石贫化率的真值(无计算误差);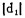
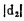
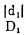

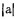
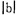
由误差理论知道
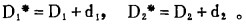
|
据此得

|
令

|
(12) |
得
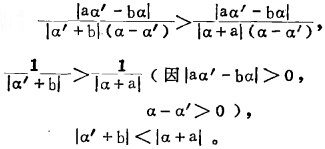
|
因
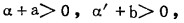
|
最终得
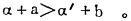
|
(13) |
通过对(13)式的讨论证明,在a、b为正、负的正常误差,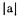
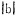
由此看出,从理论上说,用(8)式计算贫化率的相对误差比用(9)式计算的相对误差小。
2.灵敏度分析。假设n为采出矿石品位变化的灵敏性比数,0≤n=α′/α≤1。
变换(8)、(9)式:

|
(14) |

|
(15) |
为了对品位变化的灵敏性进行分析,用不同的n值代入式(14)、(15),求得如表 1所示的D1、D2值,并根据这些值绘出如附图所示的D1、D2与n值的关系曲线。
| 表 1 贫化率计算式(14)、(15)对n值变化的灵敏度 |
 |
| 点击放大 |
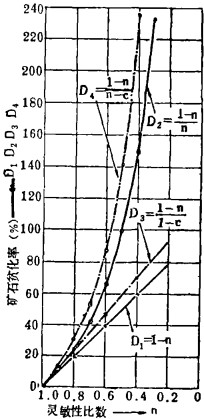 |
| 附图 D1、D2、D3、D4与n的关系图 |
从表 1和附图可看出,当n值很大时,D1与D2差别很小,尤其当n=0.9时,用式(8)和(9)算出的矿石贫化率都很小,且几乎相等;随着n值的变小,D1与D2的差别就变大,尤其当n=0.30时,用式(9)算出的矿石贫化率是用(8)式算出的3.3倍,换言之,n值愈小,即α′与α差别愈大,则D1与D2的差别也愈大。这就是比数n值变化(出矿品位与原矿品位变化时两个公式所反映的不同的灵敏性。式(14)的矿石贫化率与n是直线关系,式(15)是曲线关系,因而式(9)比式(8)对品位的变化更灵敏。
(二) 围岩含矿计算式的精确度和灵敏度分析1.精确度分析。假设D3*、D4*为矿石贫化率真值;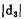
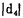

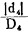
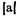
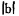

由于
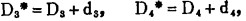
|
于是
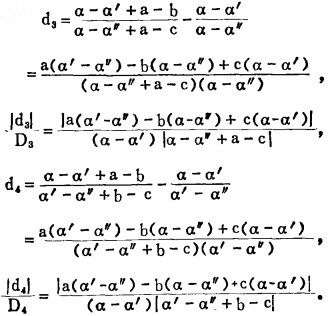
|
令
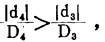
|
(16) |
得

|
因围岩品位较小,其相应误差c可近似看成零,最终得
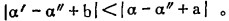
|
(17) |
通过对(17)式的讨论证明,在a、b为正负误差,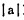
2.灵敏度分析。变换(10)、(11)式:
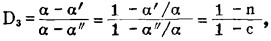
|
(18) |
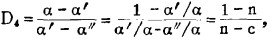
|
(19) |
式中:n—灵敏性比数,含义同前;
c—废石混入影响的品位系数,c=α″/α,它因矿山、矿种而异,一定矿山(种)的c波动于一定的数值范围,一般铜矿c= 0.125~0.167,可平均取c=0.146。
假设以某铜矿为例,取c=0.146。用相同的c值和不同的n值代入式(18)、(19),求得如表 2所示的D3、D4值,并根据这些值绘出如附图所示的D3、D4与n的关系曲线。从该表、图看出,式(11)比式(10)对品位的变化更灵敏,用不同的c值代入计算也可见证。
| 表 2 c=0.146时贫化率计算式(18)、(19)对n值变化的灵敏度 |
 |
| 点击放大 |
三 结论
根据前面分析,可得出如下结论:
1.空场类、充填类采矿法和分层崩落法、壁式崩落法等(混入废石较少,出矿品位较高)回采的矿山,废石(围岩)不含矿时,为了计算精确起见,一般用相对误差较小的D1(8)式计算矿石贫化率;废石含矿时,一般用相对误差较小的D3(10)式计算矿石贫化率。
2.分段崩落法、阶段强制或自然崩落法(混入废石较多,出矿品位较低)回采的矿山,废石不含矿时,为了有效控制放矿和加强对废石混入的监督,在放矿过程可用对出矿品位灵敏度较高的D2(9)式统计矿石贫化率,至于放矿后的最终矿石贫化率仍可用D1(8)式计算,其时不存在废石控制问题;废石含矿时,在放矿中一般用对废石较为敏感的D4(11)式统计矿石贫化率,至于采矿法最终贫化率仍可用D3(10)式计算。
3.露采矿围岩不含矿时,一般用D1(8)式计算矿石贫化率,含矿时,一般用D3(10)式计算。
| [1] |
北京钢铁学院等六院校编, 《金属矿床开采》(上册), 中国工业出版社, 1961年10月.
|
| [2] |
解世俊等编, 《金属矿床地下开采》, 冶金工业出版社. 1979年11月.
|
| [3] |
"贫化率与回采率基本原理评述", 《国外金属矿采矿》, 1983年, No. 10.
|
| [4] |
W. A. Hustrulid Editor, 《Underground Mining Methods Handbook》. Now York, 1982.
|
| [5] |
М. И. АГОШКОВ, 《РАЗРАБОТКА РуДНЫХ МЕСТОРОЖДЕНИЙ》, MOCKBA. 1954.
|
 1990, Vol. 4
1990, Vol. 4
