| 从PID到模糊控制的发展 |
在机械化的基础上实现自动化,其核心就是自动控制。现在自动控制从理论上和实践上都取得了很大成功,不仅用于生产过程控制,而且应用于社会的宏观控制。
一、 传统的过程控制模式自动控制的要求是:在没有人直接参与的情况下,利用控制装置,使被控制对象(例如,机器、设备或生产过程)自动地按照预定控制规律投入运行。从已定的设定值出发(初值),通过与现状(开始为毛坯)进行比较,得出加工的程度(如进刀深度),用控制的行话来说,就是按控制规律箅出来的加工量,命令执行机构对被加工(被控)对象进行处理,并把加工的结果再次与设定值进行比较,如此不断循环,直到加工对象与设定值相符。图 1粗略地表示了这种过程。
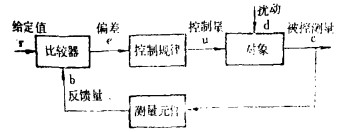 |
| 图 1 自动控制示意图 |
这是一种闭环的反馈控制方式。为了消除系统本身的不稳定和减少外界扰动的影响,反馈控制必须建立在负反馈的基础之上。它的原理是:测量元件对系统的输出(即被控制量)进行测量,测量元件的输出是反馈量b。一般而言反馈量b与被控制量C成比例。用r表示系统的输入量,称为给定值。如若是负反馈,则r与b在比较器里相减,得到偏差e, 即
e=r-b
负反馈能使系统保持稳定。例如,偏差e经过运算和放大后去控制被控制量C。设在某瞬间因系统内部和外部扰动的综合影响,使控制量C偏离希望值,使C减小,于是测量元件的输出b也随着减小,从而使偏差e上升,控制量u也上升,从而使被控制量趋向希望值。反之,如因扰动使被控制量C上升,由于负反馈同样也会使C趋向稳定。
十分明显,被控制量是否会趋向设定值,很大程度上取决于控制规律是否正确。对于单输入一单输出的生产过程,即单变量系统,控制规律往往用一个数学方程来表达。PID(比例+积分+微分)方式就是表达这类控制规律的有力工具,它具有型式:
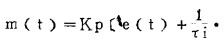
|
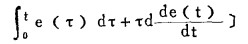
|
式中:Kp•e(t)— —比例控制项,Kp称为比例灵敏度;
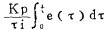
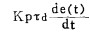
PID型式具有相当的通用性,对控制进行设计主要任务就是确立相应的各项系数,如Kp、τi和τd。过程控制的对象均为连续系统,使用PID方式的系统也不例外。
然而,使用PID控制方法的系统是一种简单的理想系统,它属于经典控制理论范畴。而在我们周围要解决的大多数系统,属于多输入— —多输出的复杂系统,它们不是能通过确定PID方程几个系数就可确定的,如窑炉系统、发酵系统……。为了解决这种系统的控制问题,逐步发展起来了新的控制论。
二、 状态空间法随着计算机的发展,一种崭新的控制理论— —现代控制理论出现了。不过,该理论使用的数学工具,倒是很久以前就有的了,只是因为有了计算机,才使这佯一种控制方法有了可能。状态空间法是现代控制理论的基础。
若一个系统用几个量来表示,如温度T、压力P和体积V等,这样用n个量表明一个系统的情况,称之为状态。这n个量所组成的n维空间称为状态空间。任何一个状态可以视为一个状态向量,表示为:
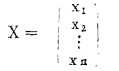
|
温度T、压力P和体积V分别可视为x1、x2和x3,如此等等。为了使X各分量分别达到预先的设定值,必然要有众多的控制量(设为r维)作用于系统,用称为输入向量U(控制向量)来表示:
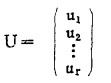
|
控制的结果将产生输出。设输出有m个量,它们可组成一个Y向量,称为输出向量,表示为:
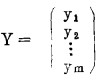
|
显然,这是个多输入一多输出系统,可用图 2表示。
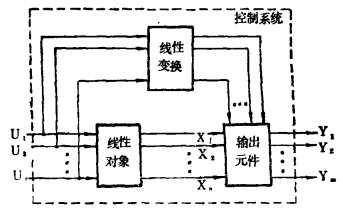 |
| 图 2 多输入一多输出系统 |
由数学演算不难得到,表明系统的状态方程为:
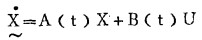
|
式中: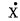
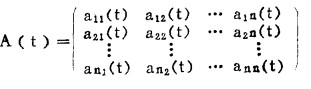
|
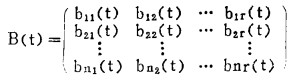
|
而输出方程为:
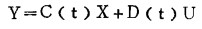
|
式中:
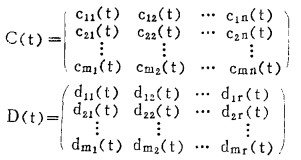
|
这两个方程是线性方程组,系数矩阵A(t), B(t),C(t)和D(t)中的t是时间,表明将随时间而改变。
解决此类系统的控制问题,可以通过各种数学工具,如先辨识系统模型,而后求其控制规律,或用自适应控制来逐步优化等等,使得系统的状态方程和输出方程更准确地反映现实情况。
然而,要求得线性方程组的解,并不容易,因为有些量是测不出来的,虽然有些量也不一定要测出。在矩阵的非对角线分量不为零时,表明向量的各分量彼此相关,相关又称为耦合,其值愈大,则耦合度愈大,系统也愈难求解,或换句话说,解的精度愈差。关于状态方程和输出方程的具体解法,可以通过线性微分方程组的解法,利用计算机借助特殊算法进行多次叠代,求出其数值解。
三、 另一种多变量系统(一)问题的提出 现代控制理论解决的是多变量线性系统的问题,对于状态方程和输出方程不是线性的系统,则难以用这种方法解决。
经典控制理论和现代控制理论有一个共同的特点,就是以事先确定数学模型为基础的,也即是说,反映客观事物的数学是以确定的值为基础的,要么是真,要么就是非真即假,其真和假的界限十分清楚。这是一种理想的情况,是把复杂的客观世界简化和标准化了。许多情况已经表明,越复杂的系统越不能要求精确,即不能用经典的精确数学去直接描述,一味追求精确将导至进入更大的谬误之中。
客观世界的确存在许多边界不清的情况,在过程控制中也是一样。“红”这样抽象的概念是几乎不可能确切定义的,因为它们带有宽的谱线连续分布。然而,作为人,有经验的学者、专家确能分辨。这说明,用精确数学难以判明的问题,却能被人的大脑所解决。
(二)例举 设有一个九管还原炉,它是用于对WO3进行还原用的。它的六组炉丝分别装在六个温区的上方和下方(见图 3),控制各组炉丝可控硅导通角即可改变各组炉丝的功率。尽管控制的是一个因素— —温度,由于六个温区分开控制,应视为六个温度变量。六根热电偶分别测量六个区域的温度。显然,各温区的温度不仅取决于本温区的炉丝导通程度,而且受其它五个温区的影响。例如,当第三温区075℃, 第五温区也为750℃时,即使第四温区完全断电,该区的温度仍可以达到300~400℃。我们用关系式:
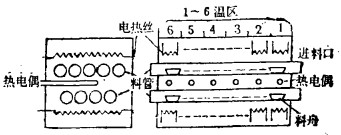 |
| 图 3 九管还原炉结构示意图 |
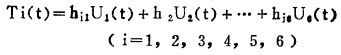
|
来描述输出方程。Ti(t)表示第i区时间t时的温度,Ui(t)表示时间t时j区控制量大小,hij表示第j区对第i区的温度影响。尽管这个系统并不复杂,由于区域之间的界限不清楚,因而,难以给hij以精确的定量描述。但是经过有经验的操作人员精心调节,是不难达到预定的温度要求750±5℃的。
所谓经验,就是一种存储于人的大脑中的知识。这种知识是否也可以放在计算机中,让计算机代替有经验的人来进行自动调节并进一步积累新的经验呢?回答是肯定的,这既有知识工程的问题,也有人工智能的问题,当前的科学技术在这两个方面正获得新的考破。
四、 模糊控制(FUZZY CONTROL)关于前述的难以建立精确数学模型的过程控制,通过知识工程和人工智能技术的发展已经取得成效。模糊控制是这类方法的一种。
模糊数学的概念是L.A.Zadel(查德)于1965年提出的,他是美国加州大学控制论专家。显然,模糊数学与过程控制是密切相关的。
下面仍以还原炉的例子阐述模糊控制系统。
(一)语言变量 若某区的温度设定值为S, 实测温度为Y, 其偏差Δe表示为Δe=Y-S,同时,第n次实测的偏差与上次实测的偏差之间的差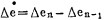
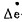
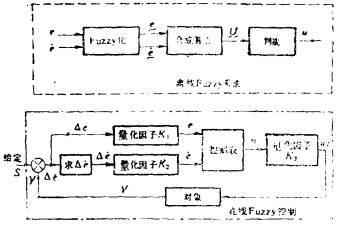 |
| K1, K2,K3—系定量化因子,用它们可以把Δe,Δe以及ui量化为e,e和u。 图 4 离线决策和在线模糊控制示意图 |
实现模糊控制的一个重要问题,就是建立语言变量。语言变量只有模糊数学才有,它不再用单一的值表示,而是值的一个集合,即在不同的测量值上有自己的属性值(其值小于1), 称为隶属度。将普通测出的输入输出值变为语言变量,建立二者的对应关系,实际上就是建立隶属度表。为了使对应关系具有普遍意义,我们应当使输入输出测量值规范化。例如,设Δe的实测值在〔a,b〕区间变化,则可规范至特定范围〔M,N〕的e,Δe和e的关系为:
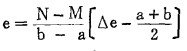
|
同理,偏差变化率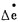
如果M=-6, N=6, 则可将偏差e分为14级,即以-6,-5,-4,-3,-2,-1,-0,+0,1,2,3,4,5,6来表示,这是测量值Δe经规范化可能达到的等级。模糊控制所要求的语言变量可分为8档:负大记为(NL) e; 同样负中— —(NM)e; 负小— —(NS)e; 负零— —(NO)e; 正零— —(PO)e, 正小— —(PS)e, 正中— —(PM)e, 正大— —(PL)e。语言变量用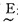
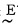
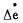
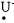
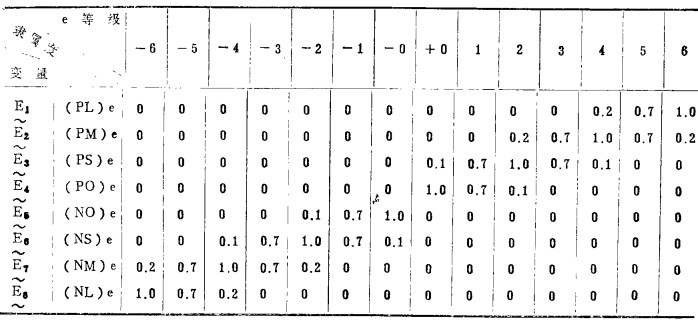
由于语言变量接近控制时操作的术语和命令,因而可根据实际操作经验建立语言变量和实测值(已规范化)之间的关系。表 1表明偏差e和相应的语言变量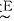
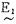
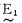
表 1 偏差e语言变量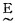 |
 |
| 点击放大 |
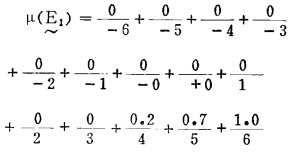
|
说明正大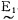
(二)控制表的建立与知识工程的关系
在知识工程中,建立知识库是最重要的工作,而知识库又是由一条条规则组成的。规则一般具有形式:
如果(if):条件1,和条件2, 和……,和条件m(成立);
那末(then):结论1, 和结论2, 和……,和结论n(决策)。按照这种形式,在模糊控制中,根据人的经验可形成一系列规则:
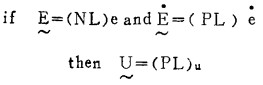
|

|
第一条规则的意思是:如果偏差为负大,并且偏差率为正大,那末控制量应调至正大。
这所有的规则组成了知识库,将所有规则通过笛卡尔积综合在一起,形成包含一切规则的总体效应,存放于计算机中。每当某种语言变量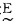
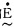
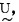
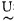
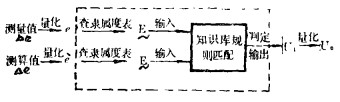 |
| u1—已规范化; u0—实际控制量。 图 5 FUZZY决策的基本过程 |
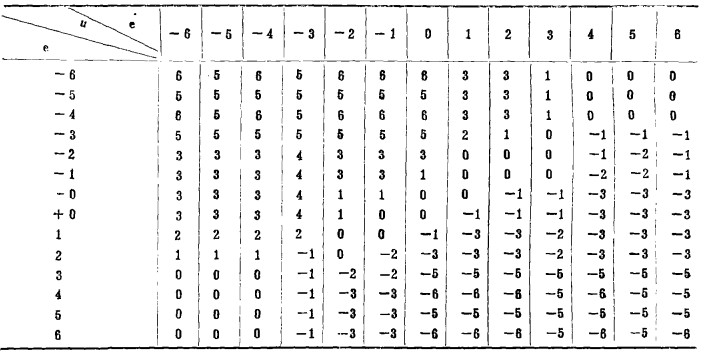
如果每经一个循环,都要这样做一遍,那末,即使计算机速度比现在快几十倍也很难满足要求。解决的办法是,将复杂的计算工作预先离线做好,制成一种控制表的形式(见表 2), 即给出测量规范化值e和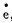
| 表 2 模糊控制决策 |
 |
| 点击放大 |
事实证明, 模糊控制可对任何能定性观测的系统进行控制, 对于参数耦合度可以侧出或可进行精确计算的系统, 模糊控制同样可行, 并且超调更小, 降低了振荡的可能, 提高了系统稳定性。
| [1] |
黄午阳.
《自动控制理论》[M]. 上海科技出版社, 1986.
|
| [2] |
潘新民.
《微型计算机控制技术》[M]. 人民邮电出版社, 1985.
|
| [3] |
王学慧, 田成方.
《微机模糊控制理论及其应用》[M]. 电子工业出版社, 1987.
|
 1990, Vol. 4
1990, Vol. 4
