| 钨矿床级差指标体系 |
矿山的建设与开采的整个过程不可避免地会遇到地质情况、国内外市场、采选技术水平……等因素的变化, 而影响采选技术条件和经营的调整和改变。且矿床开采具有明显的阶段性, 矿块的开采, 随着开采工程的发展, 也具有明显的阶段性、前移性及其沉没成本的不可收回性。随着我国经济体制深入发展, 计划经济体制正在加速向商品经济转变, 矿山企业的生产经营决策应在市场的引导下进行, 中心环节是提高企业的经济效益, 增强企业活力。因此, 工业指标不应该是一个一成不变的参数。
首先, 工业指标不应该是“最低标准”, 而是“用来衡量矿石质量和矿体开采条件能否在一定工业经济技术水平条件下, 得到最合理地利用的标准”。钨矿产品素来都是出口物资, 生产最多的钨矿产品不是企业的目的, 企业对钨产品均生产目的是利用国家的钨矿资源, 通过对钨矿的开采, 而获得最佳的经济利益。因此, 企业的工业指标应能适应采选科学技术水平、国内外市场……等因素的变化, 保持技术与经济之间的最佳关系, 求得经济的有效性, 取得最佳的经济效益。其次, 矿山生产建设、从投产到闭矿, 经历基建投资还本利期、生产经营高峰期和闭坑收缩期三个阶段, 矿体的开采也分为开拓、采准、回采等阶段。生产矿山在不同阶段, 有不同的经营目标和成本结构, 同样, 矿体在不同开采阶段, 具有不同的成本结构。在矿山的储量管理中, 一是应保持合理的经济关系, 二是应保护国家矿产资源。工业指标应能适应矿山建设和矿体开采的阶段性及其相对应的经济关系。
因此, 生产矿山的矿床工业指标, 要在原工业指标宏观控制下, 结合矿山建设的生产阶段、矿体(块)开采阶段, 采选科技进步、国内外市场等诸因素, 对具体的“时、空”条件下的开采范围的工业指标, 进行调整或修订, 建立一套适合于某一段时期、某一开采范围的工业指标。这样才能使矿山企业适应瞬息万变的外部环境和潜移默化的内部环境。
二 工业指标的经济性钨矿床工业指标, 沿用工程指标体系, 如边界品位、最低工业品位、最小可采厚度、夹石剔除厚度、最低米百分比, 因有两个品位指标, 故也叫作双指标体系, 而这两个品位指标, 又是核心指标。
边界品位是用来确定矿与非矿之间的界线指标。边界品位指标的确定, 主要着眼于:
1.尽量保证矿体的完整性, 使矿体的空间状态尽可能地简单一些;
2.要保证圈定的矿块达到最低工业品位要求, 在经济上, 它是最低工业品位指标试算和核定的中间产物, 本身没有明确的经济意义;
3.最大限度地利用矿产资源, 按边界品位指标等于尾矿品位的1.5 ~ 2倍经验法确定。
最低工业品位是单项工程平均品位的最低要求, 也是圈定工业矿石的最低品位要求, 低于最低工业品位的某特定储量范围的矿石为表外矿, 反之为表内矿, 通常采用价格法和类比法确定, 以收文平衡品位作为指标依据, 在经济上具有较为明确的意义, 即保证某特定储量范围的开采, 能不致于亏损, 对已圈定的特定储量范围的经济效果起校核作用。实际中, 特定储量范围并没有明确的规定。
可见, 工程指标体系是在经济不赔不赚, 而能最大限度地利用矿产资源的原则基础上建立起来的。
在欧美各国均采用矿块指标体系, 也称为单指标体系, 在最小开采单元中用边际品位来圈定矿块, 计算储量。不仅用边际品位来决定单个矿块、开采单元或矿堆的取舍, 还用它来指导矿山企业进行计划和决策。矿块指标体系是以最佳经济效益为决策目标, 以充分利用矿产资源的经济价值为原则而建立的。
上述品位指标体系, 各有利弊。在钨矿山矿床新的品位指标体系建立过程中, 应紧密结合生产矿山实际, 取精弃粕, 加以发展和完善, 形成一套科学的指标体系。矿块指标体系采用单一边界指标, 能简支地反映工业指标的经济目的, 取得最佳的经济效益, 这是单指标体系可贵之处, 且工程指标体系能为矿床提供一个明确均矿体形态, 并尽量保证其完整性, 有利于资源的充分利用和保护。
最低工业指标, 是一个经济效果考核指标, 当边界品位指标保证应有的经济效果后, 可以不使用这个指标。这样, 边界品位指标的经济意义比较接近于矿块指标体系的边际品位。此时, 边界品位指标并非用于确定矿与非矿间的界线, 边际品位和边界品位不同点, 在于前者是以矿床宏观最佳效益为前提, 后者则以矿床开采最低经营目标为确定依据, 从矿床微观角度去求其合理性, 而且它也不一定是以最小开采单元来计算品位和储量。钨生产矿山级差边界品位有三方面的意义:一是在空间上它是可采矿体边缘每个质点的品位, 故可将之用来圈定可采矿体, 决定矿床密度函数统计单元矿量的取舍, 二是在经济上反映了企业对矿床开采最低经营目标, 是企业对最低可采矿石的经济要求, 从微观角度去求得矿床经营参数的合理性, 三是边界品位以级差品位的形式表示时, 它表明开采阶段的阶段性、前移性及其成本沉没的不可回收性, 并可用于圈定矿块。
三 生产矿山矿床工业指标的合理性生产矿山的生产能力已定, 已形成固定的生产规模, 已具备生产经营实践, 能准确地把握生产经营状况及其参数, 其生产系统、管理机构、生活服务设施和机构、职工队伍等均已形成; 且生产矿山品位指标是矿山生产各个时期生产经营目标和条件的综合反映, 是微观指标。而勘探、设计阶段的经营参数是整个矿床的宏观指标。二者经营参数的确定不同。
钨矿企业内外部条件差别很大, 矿山生产建设处于不同建设期, 生产经营条件各异, 在进行经营参数分析和决策时应认真考虑科学决策。投产初期的矿山, 产品收入除抵销正常成本开支外, 还需偿还货款和利息, 建设中期的矿山, 进入生产经营高峰期, 晚期矿山进入矿山建设收缩阶段, 资源频于枯竭, 开采难度加大, 成本上升。这里引入“矿床开采最低经营目标”的概念, 来讨论经营参数的决策问题, 最低经营目标是对矿床每个微小矿块(统计单元)开采所产生的生产经营效果的最低要求, 各企业由于经营条件和状况不同, 最低经营目标也不同, 一般情况下, 企业的最低经营目标应是不赔不赚。当企业生产能力和采选技术较为稳定时, 盈亏平衡的原矿品位为:
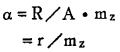
|
(1) |
式中: R——年矿石生产总成本;
A——年原矿处理量;
r——每吨矿石生产成本;
mz——原矿中, 每吨金属的产值。
如果矿体边界αb为平衡品位α时, 由《钨矿床优化模型》〔5〕可知, 此时, 为最优边界品位, 可使矿床获得最大盈利。
企业的经营目标是企业在一定时期内的经营目的, 如盈利指标, 是通过一段时期对若干开采矿块的平均品位来实现。因此, 可将企业的经营目标理解为宏观指标, 而对微小矿块开采经济目的即最低经营目标为微观指标。
当矿床的边界品位以最低经营目标来确定时, 如果其目标为“不赔不赚”, 恰等于生产成本r, 可使矿床获得最大盈利, 对有条件的矿山, 应以r来确定最低经营目标和边界品位指标。但对一些自然丰度较低的矿床, 尤其对那些资源频于枯竭, 开采难度大, 生产成本高的晚期矿山, 要以“不赔不赚”作为最低经营目标往往是不可能的。以生产成本r来确定边界品位指标, 将可能导致无矿可采, 难于圈出矿体。因此, 对这类矿山, 不应该以生产成本来确定其最低经营目标, 对一个企业不管矿床自然丰度怎样地低, 生产经营条件怎样地差, 最低的“最低经营目标”应该是收回采、选和经营中所消耗的材料和电力等变动成本费用, 即将供过于求的钨矿产品去换取社会上还较紧缺的钢材、木材, 电力、燃料……等物资, 至于工人工资福利费、通风排水费、管理费……等固定费用, 认为只要企业还存在, 即使不生产, 这些费用反正都得支出, 且在生产经营过程中也不一定都收回, 因而最低经营目标等于变动成本, 即最低经营目标的最低极限值。由《钨矿企业生产经营分析模式》可知, 以变动成本来确定边界品位, 此时:
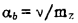
|
(2) |
式中: v—变动成本。
边界品位αb也是最低极限边界品位。
由(1)(2)式不难看出, 边界品位指标等于企业最低经营目标b与原矿的单位属产值mz之比:
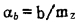
|
(3) |
企业的最低经营目标只能在收回全部成本和收回变动成本之间进行选择。技收回全部成本计算, 可以使矿床获得最大盈利, 而当目标值b小于变动成本费用、时, 处理的低于最低极限品位的原矿越多, 经济效果越差〔4〕。界于这两者之间的企业, 比如条件较好的晚期矿山, 尽管资源即将枯竭, 但部分劳动力可以通过多种经营而疏散和横向联合开发新产品, 最低经营目标不仅仅是收回变动成本, 而且还应该回收工资福利费fg和部分企管费f'g, 此时, 边界品位:
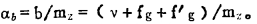
|
总之, 企业最低经营目标及边界品位, 应根据生产矿山的具休情况而定。至于工程指标体系, 矿床的工业指标确定和计算储量的着眼点, 则是最大限度利用资源, 如果一旦将着眼点放在“资源价值的利用”上, 由于边界品位提高, 势必导致不少企业(含新老矿山)无矿可采。为使生产持续正常进行, 应在原工业指标的宏观控制下确定边界品位指标, 矿体形态不应有过大的变化, 资源条件好的矿山, 原则上应以最大盈利为目标,资源条件差的矿山, 开始不应将目标定得过高, 应随企业改革的进程, 和实行“一业为主多种经营”来降低成本增强企业活力, 而逐步提高目标。
四 边界品位指标与矿体开采的阶段性地下开采从开拓到出矿, 具有明显的阶段性、前移性及其沉没成本的不可收回性。随着开拓、采准、切割工程的完成, 矿体的自然形态和品位分布将进一步揭露, 储量级别随之提高。为使矿块或矿段的开采设计与实际相吻合, 需对矿体进行重新圈定。本着对矿产资源的充分利用和经济上的合理性、考虑各开采阶段成本的阶段性和沉没性, 应建立级差品位体系, 矿堆的取舍, 采场二次贫化后的低品位矿石及地表民窿废石的取舍决策, 崩落采矿法最终放矿矿石品位的决定, 都应该以级差品位指标为准绳。
现以地下开采的矿床为例, 进行各开采阶段的级差品位计算。地下开采的、开拓、采准、回采三个生产阶段, 相应地有对应的三级矿量和存窿矿石, 按其成本的不可回收性和矿山企业的最低经营目标, 级差边界品位为:

|
(4) |
式中rx为矿块开采过程中巳支付的成本费用。在级差品位计算中, 用得最多的是备采阶段级差边界品位指标, 当矿块作好切割工程后, 一般需对矿块进行重新圈定, 称为二次圈定。此时, rx为开拓、采准、切割费用之和, 而存窿矿石的取舍, 则还需加上回采费用。
在进行级差品位计算时, 首先需进行生产成本的分解, 先将企业的生产成本分为接作业成本和非作业成本两大部分, 然后根据矿石开采, 加工、产品出售的阶段性将直接作业成本分为:开拓、采准、切割、回采及其他等费用, 非作业成本则含管理、通风、排水、提升运输、维简等费用。确定各阶段开采费用, 可根据各作业成本与非作业成本的关系, 将各项非作业成本分摊到各项直接作业项目中去计算, 切忌从财务成本中直接照搬。
五 生产矿山矿床工业指标的有效性矿山企业应在市场的引导下, 确定与之相适应的品位, 使矿床在整个开采过程中获得最大盈利。据对某些矿床经济分析, 我国采用的工程体系指标中, 所采用的边界品位指标, 由于过份地强调资源利用, 不仅远低于最优边界品位指标, 而且还低于最低极限边界品位, 把大量经济上不合理的品位样点圈入矿体, 人为地降低了经济效益。
然而, 工程指标体系的边界品位的确定, 能尽量保证矿体的完整性, 使矿体开采尽可能显得简单些, 并且可保证利用选矿、冶金技术, 充分回收资源, 这是工程指标体系优于矿块指标体系之处。但矿体是被开发利用的对象, 充分地考虑对象的被利用的可能性和难易程度, 是确立品位指标的必要条件, 正确地圈定矿体, 必须对矿床地质特征, 矿体形态、产状及其变化规律, 矿体与围岩的关系, 有益和有害组份的赋存状态, 以及后期地质构造的影响等, 进行详细的地质分析研究, 而工程指标体系的边界品位的确定, 考虑了上述关系和指标的有效性。
根据企业最低经营目标确立的合理性, 毫无疑问, 生产矿山应以级差品位作为边界品位指标来圈定矿体。同时, 为使矿体保证满足上述地质关系和指标的有效性, 对于各类不同矿床类型, 各种自然丰度及其不同品位变异性的矿床, 在圈定过程中, 应吸取工程指标体系之所长, 使矿体能具有较好的完整性并符合其自然形态。
对品位分布变化较为均衡的矿床, 直接以级差品位作为边界品位指标, 按样点品位进行圈定矿体, 容易如愿以偿地圈出矿体, 计算储量, 既能形成完整的矿体自然形态, 又能取得最符合予期目标的最佳经济效果, 如图一中斜线部分。
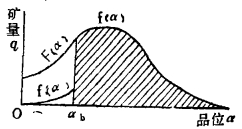 |
| 图 1 品位变异性小的矿床矿体函致圈 |
F(∝)为矿床样点密度函数即全部勘探样点密度函数, f (∝)为高于边界品位以b的矿体样点密度函数, f'(α)为低于边界品位的矿体样点密度函数。品位变异性小的矿床, 低于边界品位的样点f'(α)能排除出矿体之外, f'(α)接近于q = 0函数, 而高于边界品位的样点又能最大限度地圈入矿体, 使f(α)接近于F(α), 在矿体中能满足造成贫化的f'(α)的样点最少, 取得效益实现目标的f(α)中的样点, 最大限度地圈入矿体。
对于品位变化均衡性较差、自然丰度较差的矿床, 以级差品位指标按样点品位来圈定矿体, 往往就难于圈出符合矿体自然形态的完整矿体, 如脉状矿体, 可能圈定若干断断续续的扁豆状或透镜状矿体。为使矿体便于开采, 既可能会不恰当地把大量低品位样点圈入矿体, 也有可能过份地将高品位样点丢失。
图 2中斜线部分为圈定的矿体, 密度函数f(α)与f'(α)的函数分布状态与矿体圈定的地质技术密切相关。在最低经营目标所确定的指标条件下, 同时应以最佳的地质技术来圈定矿体, 才能保证最佳的经济效果。通过最佳的地质技术使样点密度函数f'(α)能最接近q=0; f(α)最接近于F(α)。
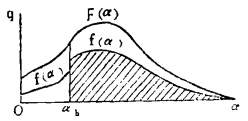 |
| 图 2 品位变异性大的矿床、矿体函数图 |
一般工业品位指标计算的方法是对具体矿床考虑经济性和有效性的方案比较法, 如总现值法、总盈利法、级差矿利法和方案对比法, 这些都是一步骤的方案法。在此, 推荐两种二步骤的指标确定方法, 以便进一步说明按最低经营目标所确的边界品位指标的不可动摇性和地质技术适应的必要性, 寻求一种适合各种自然丰度和品位变异性的最优指标和圈定方法, 使圈定的矿体开采后经济上最佳。其方法是在已确定的边界品位的基础上, 吸取了工程指标体系对矿体形态重视之长处。现分述如下:
1.最小统计单元法, 将矿床划分成许多统计单元, 统计单元的品位由所包含的样点品位计算出为ξ, 矿床的密度函数则为F (ξ)。矿床圈定时, 通过相宜的统计单元形式和规模来适应各种矿床类型、地质条件以及品位分布特征的矿床, 使矿体在已确定的边界品位条件下, 被圈成符合自然形态而又便于开采。
对一个具体矿床, 在圈定矿体时, 如果统计单元的规模过小, 难于圈定出可靠而又便于开采的矿体, 尽管采用了合理的边界品位指标, 而达不到最佳的效果, 过大的统计单元, 能很容易地圈出矿体, 并易使贫点函数f’(ξ)接近q=0, 富点函数f(ξ)接近于F(ξ)。若统计单元过大, 容易把许多低品位样点被统计单元所掩盖而圈入矿体中, 使f'(α)远离q = 0, 造成矿体过大的贫化, 达不到最佳的经济效果。
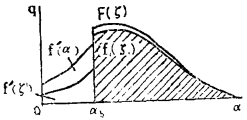 |
| 图 3 矿床(矿体)统计单元密度函数曲线 |
因此, 最小统计单元法就是以αb为边界品位圈定矿体时, 在满足贫点函数f'(ξ)为q = 0, 富点函数f (ξ)接近F(ξ)和矿体有较好的可采性的同时, 使统计单元最小。统计单元的规模大小是由矿床地质特征和品位变异性质, 边界品位的高低所决定。其规模最小可能是一个样点的储量, 最大可能是一个矿段。同时, 由于统计单元表示了一定储量计算范围, 计算边界品位指标时应将开采贫化率考虑进去:
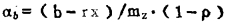
|
(5) |
当储量计算的范围较大时, 如果各个不同的部位地质特征和品位的变异性较大, 应该根据具体情况, 选择几种不同大小的统计单元规模与之相适应, 达到最佳的效果。
2.经验法:矿山地质专家在具有明确的最合理的边界品位指标同时, 根据矿床的地质特征, 尽可能地剔除低于边界品位的样点, 保留高于达界品位的样点, 圈出便于开采矿体。对子品位变化较大的矿床, 还需按(5)式所计算的指标对矿块平均品位进行校核。此法为国内惯用的工程体系矿体圈定方法。
结语钨矿企业受计划经济影响, 技术设备落后, 劳动生产率低, 机构庞大, 生产成本高, 促使边界品位指标很高, 难于决断, 究其原因:一是按经验法确定边界品位, 未从经济上加以考虑, 指标偏低, 二是钨矿企业生产成本高。钨矿企业只有按经济规律办事, 尽快取得效益, 才能以较多的财力开展多种经营, 开发新产品, 开拓新市场, 加强横向联合, 疏散劳动力, 减轻企业负担, 在竟争中建立起经济良性循环, 降低成本, 下降边界品位, 充分利用国家资源。
 1988, Vol. 2
1988, Vol. 2
