| 钨矿床品位指标优化模型 |
十三大报告指出:“为了实现产业结构和企业组织结构合理化,达到资源优化配置,不仅要发挥市场和自由竞争的作用,而且要依靠国家制定正确的产业政策和企业组织结构政策,并运用价格、财政、税收、信贷等经济杠杆来进行干预和调节,以改革促进经济的健康发展,以发展为改革创造较好的经济环境。这样,就有可能把发展和改革、计划和市场、宏观管理和微观搡活结合起来,并在计划工作上走出一条新的路子。”
在新的经济运行机制下,矿山企业应努力做到“经营参数最佳化,目标利润极大化。”矿床的开采过程中,经营参数便是矿石的品位指标。矿山企业应该在市场的引导下,采用灵活的经营技巧,在保证矿山企业盈利的基础上,确定与之相适应的品位指标,迸而更加经济合理地开采矿床。
目前,对我国习用的“双指标体系”已有较多的批评,对“单指标体系”持欢迎态度的人越来越多。“优化模型”所建立的最优准则,既可适应于单指标体系,也可适应双指标体系。即不论在那种指标体系下,它都是最优的。这里的最优标准,是使矿床在整个开采过程中获得最大盈利。模型对矿山价值,定义了一个最优边界品位,相应的价值便是国家所能得到的基本收益。接下来定义了一个开采函数序列,可以运用最优开采函数的方法,指导矿山进行灵活的经营,这个构想,是对矿山企业如何体现“宏观管理与微观搞活结合起来”的探索。
(一) 基本模型确定矿床工业指标,应从储量计算开始。通常将矿床区域设为Ω,在任一座标点Pxyz上,品位为f (Pxyz),若品位和空间座标的关系f (x)已知,则矿床的总金属为:
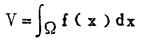
|
(1) |
显然,一般情况下,f (x)是个随机变量,即使在离散的情况下,通过各中段各勘探线上的样点求和:
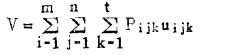
|
(2) |
(式中:Pijk—第i中段、第j勘探线、第k样点的品位,Uijk—相应于Pijk的矿石量)。
式中Pijk也仍然是个随机变量。图 1是三条勘探线上的品位变化关系。不难看出,通过式(1)、(2)计算储量,特别是给出品位与储量的关系,是很困难的。
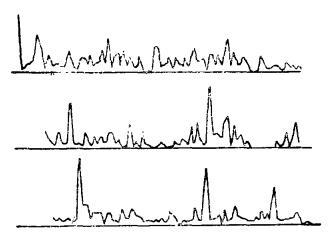 |
| 图 1 表征品位空间随机性的三条折线 |
传统统计法,根本的弱点是不考虑矿其平均品位为床的赋存特点。因此,在实际运用上有很大的出入,当然,如果通过深入研究,对偏离实际值的程変作出活计,统计法仍不失为一个很好的方法。最重要的是,统计法有它深刻的数字背景。如果对储量与品位的关系是用于评价时,我们傾向用统计法,甚至运用抽样分析和假设检验的方法。
作为矿床设计,为提供足以信赖的模型,我们采用如下方法获得矿床品位的密度函数:
1) 通过CKCG软件,按品位圈出矿体,并算出矿量;
2) 采用函数逼近的方法或者用数理统计的方法求出密度函数。
这样建立的数学模型,便是一个确定性的数字模型。这与计算机技术的发展是分不开的。
密度函数f(ξ), 是一个描述矿床品位间密度关系的变量•对不同的矿床矿山对应不同的密度函数。不过,密度函数服从对数正态分布规律。这一规律在建立密度函数时可以参考。
f(ξ)确定后, 矿床的总金属量即由下式确定:
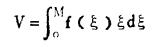
|
(3) |
式中M为品位的上限。
矿床中的平均品位为总金属量与总矿石量之商,即:
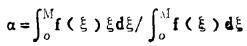
|
(4) |
相应地,对于品位M>ξ≥x的金属量为
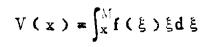
|
(5) |
其平均品位为
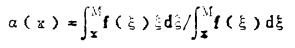
|
(6) |
在密度函数确定之后,储量与品位的关系也就随之确定。作为今后计算分析的依据,不难说明(5)、(6)式具有如下性质:
1) v(o)=V, v(M)=0;
2) v (x) ≥ 0,且为关于x的非增函数;
3) v (x)关于x连续;
4) α (x) ≥ 0, 且为关于x的非降函数。
其次,对密度函数f(ξ)除以V,则得到与槪率论中一致的密度函数。
(二) 贫化函数与开采函数矿石贫化率问题是与品位变异有关的问题。但在采矿方法确定之后,便可利用一定的地质技术,预先将废石量圈入矿块中.在图 2所示的斜线部分即为废石量。这里不考虑品位为O的废石,而将它们视为带有一定矿量的围岩,这对于细脉型和细脉侵染型矿床,这种假设是合理的.
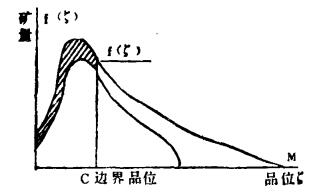 |
| 图 2 贫化函教与开采函数示意 |
这里定义贫化函数ψ (ξ)为:品位ξ的废石混入量。它由品位的变异性质所确定,对应于不同的采矿方法,并可以允许不同的夹石厚度。结合矿体圈定,采用与建立密度函数F(ξ)相应的方法求出。考虑到矿石品位分布的随机性,不妨认为ψ (ξ)与f (ξ)有相同的形式。
因此,在给定边界品位X和求出ψ (ξ)以后,矿石贫化率即可按下二式分别计算:
1) 直接法:
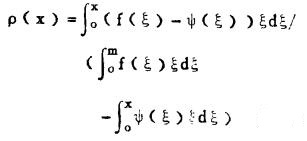
|
(7) |
2) 间接法:
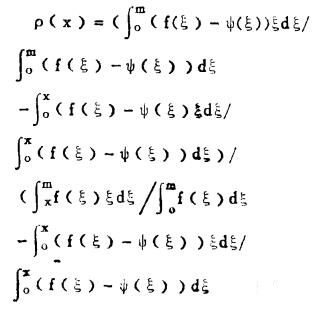
|
(8) |
当然,在设计中也可以不单独计算贫化率,而将废石直接圈入矿体,然后给出整个矿体的平均品位。此略。
类似于贫化函数,可以定义开采函数φ(ξ),φ(ξ)为品位匕的开采矿量。显然,在开采品位确定之后,开采的全部金属量由(5)式给出,而对于计划中的开采金属量,则由下式确定:
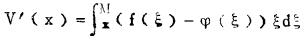
|
(9) |
图 2中阴影部分即为V'(x)。显然开采函数是由生产经营中的各种因素所确定的。对开采函数的深入研究,是提高企业经济效益的重要途径之一。
(三) 最优开采品位根据“生产经营分析漠型”可导出矿山对品位ξ≥X的矿床开采的盈利为:
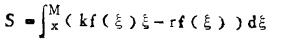
|
(10) |
式中: k=(P2 — Tz)(1-ηz)εz/βz为原矿中每吨金属产值
Pz—产品价格
Tz—矿外加工费
ηz—产品销售税率
εz—选矿实收率
βz—精矿品位
最优开采品位的准则,可以从不同角度提出,例如,使矿床获得最大盈利,使矿床开采最多金属等等。我们取前者,即,最优开采品位是保证矿床在开采中能获取最好的经济效益。
以(10)式为优化的目标函数,对它取极大:
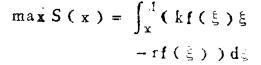
|
(11) |
由于f(ξ)为连续函数,且g(ξ)=kξ-r在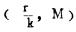
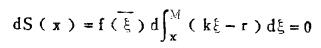
|
极值为:x. = r/k
且:d2δ(x.) < 0)。
这一结论证明了,在不考虑约束和任何的矿床密度函数的条件下,矿床的最优开采品位与矿床的分布形式无关,取决于获得最大总盈利的下限品位,即其最优开采品位为经济平衡品位。
在单指标体系中,可以将其作为边界品位。
如果以最优开采品位x.作为最低工业品位,则可以通过式(6)导出准边界品位公式:
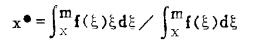
|
(12) |
由(12)确定的准边界品位,是保证平均品位能达到x.的品位。即矿山按此品位开采,可在不亏的前提下,开采出最多的资源。显然,矿山的经济效益是很差的.
我们建议,在原则上应以最优开采品位为边界品位,但为了实现矿体完整性,在圈定矿块时,应采取必要的地质技术手段进行。
在资源利用与盈利上有过较多的争议,可在新的经济体制下得到解决。事实上也只有利用经济的杠杆,组织企业有自主权的生产,才能从根本上改变我国经济结构不合理的局面。根据投入产出的方法,可以证明开采低于平衡品位的资源,实际上也是一种对资源和能源的浪费。
(四) 开采函数序列由(9)所定义的开采金属量,是在不考虑时间因素的开采函数下所开采的,因此,用此式不便于进行动态计算。
现在讨论开采函数序列。如果本期开采期为n年,即分为n个阶段进行,且每个阶段有m个排产方案构成m个不同的开采函数,则可定义幵采函数序列φij(ξ),相应的开采量为:
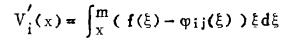
|
(13) |
每个阶段及整个开采期的金属量分别为:
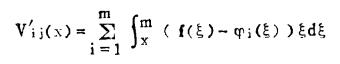
|
(14) |
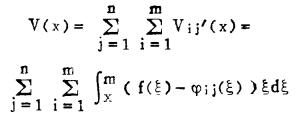
|
(15) |
为简洁起见,只考虑每年只有一个方案,即:
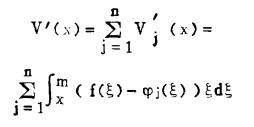
|
(15') |
相应于(10)式,每个开采阶段的盈利为:
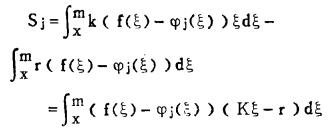
|
(16) |
则总盈利为:
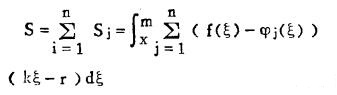
|
(17) |
设利率为i, 设n为开采年限,则得到在第j个开采阶段的在本期开采结束时的总金额:
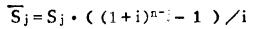
|
(18) |
因此,全矿在整个开采期间所获得的总金额为:
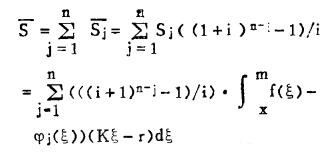
|
(19) |
aj = ((1 + i) n-: - 1) /i,则aj为递减序列。不难证明,仅当Si为递减序列时,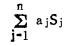
可以构造函数,
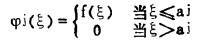
|
(20) |
其中,M = a0≥a1≥a2≥aj… ≥an=x.可以由下式确定aj.
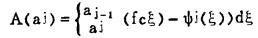
|
(21) |
A(aj)为第j年矿山的最大矿石处理能力。可以证明由(20)所定义的开采函数序列为最优开采函数序列。虽然在实际生产中很难实现,但尽可能靠近最优开采函数应是一条矿山排产的原则。
在矿山初期阶段采高品位矿石,以改善投产初期的经济效果。事实上,应该在整个开采期间内贯彻这一原则:富矿优先。这个结论,也可以由动态规划理论予以证明。
在采矿工程中,随着矿山地压管理技术的提高和经济观念的树立,人们对“由上到下、由上盘到下盘、由两翼到中央或由中央到两翼,贫富兼采……”等矿床开采顺序与准则有着更加全面的理解。例如,运用合理的充填技术,就可以不受上述顺序的制约。通过对坚固围岩的急倾剁脉群矿床的地压研究,认识到采深200~300M, 采空区100万M3以后才可能产生地压,而且现代岩石力学丰富的计算方法,可以对矿山地压作出预测预报,这就意味着,矿山开采并非一定要严格遵循上述顺序,这样就大大地提高了矿床开采的灵活性和经济效益。
最后,证明在动态规划下,最优开采品位,与静态一致,都是经济平衡品位。由(19),令,Z(ξ) = f(ξ)-
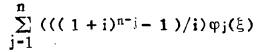
|
(22) |
这里Z(ξ)在〔x、M〕上有界,且有有限多个间断点的函数,在这些间断点的ξ.i的ε邻域内定义连续函数Z(ξ),则得到新函数:
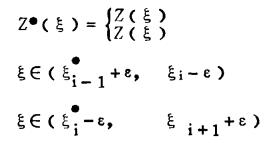
|
(19)式则为:
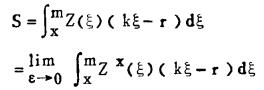
|
此时,用第三节的方法,即可得到x. = r/k.
(五) 储量管理系统CKCG软件简介储量管理系统软件CKCG是为了适应某钨矿的经济技术优化而研制的。该矿的勘探网度(60~120米)× (50~100米),在勘探线上连续取样.因而样点密集,数据齐全。
应用这个软件,分析了某钨矿的品位一储量关系,按最优开采顺序排产。计算结果说明,该矿经过优化后,可以取得极其显著的经济效果。目前,CKCG软件正在不断完善之中。同时,计划使其能在排产中考虑矿山地压因素等问题。下面对现有的二个部分作一简介:
1.勘探样点数据库
数据结构层次清晰,查找与修改都很方便,是矿山生产经营实现动态管理的基础。经对每个样点加以岩怵条件的内容,便可用于考虑地压问题。
2.应用软件库
应用软件库里存贮了各种基本程序,如统计分析程序、优化程序、回归分析程序等》其中,最重要的是矿块圈定程序和预排产程序。
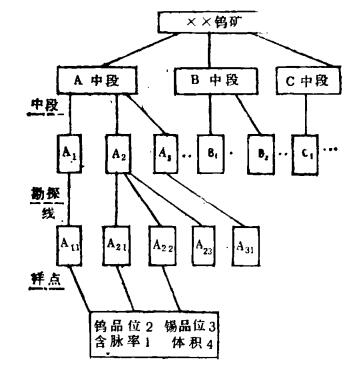 |
| 图 3 数据结构图 |
两个程序的主框图如下:
两个程序用basic语言写成,具有人机对话功能,屏幕上汉字显示,为矿山生产经营决策起了有力的助手作用。
程序在IBM—PC/XT微机上实现。
结语某一地质及开采条件均较好的中型钨矿,因矿床工业指标确定时,未进行系统的经济分析,投产后年亏损160—220万元。通过生产经营分析,改变产品结构,提高处理能力,预讨年盈利万亓》尤其是矿床经营模式优化后,效益得到了大幅良提高.该矿勘探和基建费xxx万元,按原工业指标进行开采,失去偿还能力,优化后xx年即可偿还全部基建投资。可见,矿床经营指标优化,能庚一个开采意义不大的矿床转变为有开采价值。
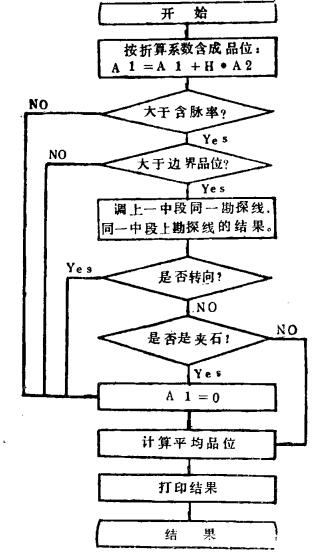 |
| 图 4 矿块圈画程序主框图 |
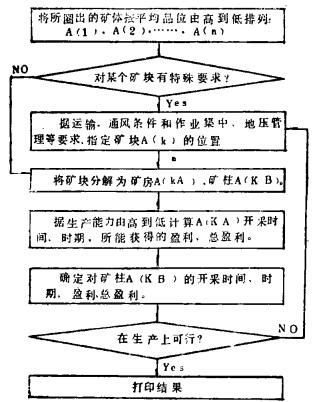 |
| 图 5 预排产程序主框图 |
随着改萆开放的深入,我匡蔌的经济运冇积制为企业提供了更为广阔的天地。钨矿企业应该审时度势,改变技术落后,管理落后,靠消耗大量资源来发展经济和开采不合理的矿产资源、浪费资源与社会财富的做法,才能使老矿获得新生。
 1988, Vol. 2
1988, Vol. 2
