| 旋转塔形螺旋溜槽液流特性的研究 |
螺旋选矿机自从美国I.B.汉弗莱于1641年试制成功以来,以其结构简单,生产成本低,处理能力大及操作容易等优点引起选矿工作者的兴趣与重视,相继有苏联、东德、澳大利亚以及南非等国家试验和研制成各种型号与规格的螺旋选矿机,至今已获得了很大的发展,是世界上正在使用的重选设备中最普通的一种。已广泛应用于选别赤铁矿、钛铁矿、钨矿、砂锡矿以及一些稀有金属等矿物。
在理论研究方面亦有很大的发展,60年代苏联选矿学者M.Ф.阿尼金对螺旋水流的运动结构和矿粒运动规律进行了研究[1];80年代加拿大学者R.O.布特以及苏联A.V.雅辛对螺旋溜槽的现代化设计与生产发展方向进行了研究[2]。我国自1955年开始研究螺旋选矿机,最早由广西平桂矿务局等单位用轮胎制成螺旋选矿机,用于选别平桂地区砂锡矿石。60年代后随着陆地沉积砂矿、海滨砂矿的开发以及铁矿石的大量利用,有更多的单位从事螺旋选矿机、螺旋溜槽的研究。至今在国内已研究出多种型式的螺旋选矿设备,如以溜槽横断面形状来区分有立方抛物线型、复合椭圆型、平底型以及正锥型的螺旋溜槽等,70年代末出现了旋转螺旋溜槽。对螺旋溜槽分选机理的研究,我国已做了大量的研究工作,其中如范象波、卢继美等专家分别对螺旋结构最优化,流膜特性等方面进行了卓有成效的研究。
螺旋溜槽已成为一种细粒重选设备,在国内外得到了广泛发展,但是随着选矿技术指标要求不断提高,该设备也暴露了一些弱点,如回收粒度下限仍不理想,一般大于30 ~50微米,并且现今面临资源利用日趋贫、细,也急待延伸螺旋溜槽回收粒度下限。本文针对上述问题从理论上探讨了旋转塔形螺旋溜槽的液流特性。试验采用的设备,主要结构参数如下:
溜槽横断面特性为立方抛物线型,其特性方程为:
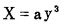
|
(1) |
式中:a——为系数。
螺距的变化用下式表示:
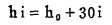
|
(2) |
式中:hi——为第i圈螺距;
h0——为基数值70毫米。
溜槽构成的锥台:上底直径为240毫米,下底直径为400毫米,锥台高为1050毫米。还值得提出的螺旋槽面各点的纵向倾角β、横向倾角α均属变化的。
一 螺旋溜槽两相流雷诺数的研究早在1880年雷诺通过实验[3],发现流体运动有层流和紊流两种不同的流态,以因次式来表示,称雷诺数Re即:
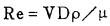
|
(3) |
式中:V——为流体平均流速;
D——为流管直径;
P——为流体密度;
μ——为流体粘度。
(3)式中的直径D也可以用过流断面其他特性尺寸来表示,如溜槽用过流水层厚度H来表示。
国内外曾有学者从不同流态出发研究流膜分选机理,迄今形成两种截然不同的理论。紊流作用理论认为:由于流膜层间存在速度梯度,使流体质点发生旋转,形成旋涡,当流体质点产生较大的压力差时,此流体质点即产生升举力,促使流体质点互相交换,形成紊流的咏动作用。在溜槽中就是利用脉动水流所产生的紊动压力使矿粒悬浮、松散、析离分层,但是在生产实践中发现,随着矿浆紊流程度的增加,细粒有用矿物的损失也增加。英国学者拜格诺德(R.A. Bagnold)著名的层间剪切理论[4],通过实验提出:当悬浮液中固体颗粒连续受到剪切应力作用时,在垂直于剪切方向将产生一种分散压,使颗粒有向两侧分散的倾向,以降低切应力,分散压力的大小达到使相当一部分顆粒在分散压和重力间平衡时,保持悬浮状态,同时在试验中确定了剪切应力和分散压的大小,得出经验公式(略),拜格诺德假说较正确地解释了在层流情况下矿粒悬浮分层的机理。
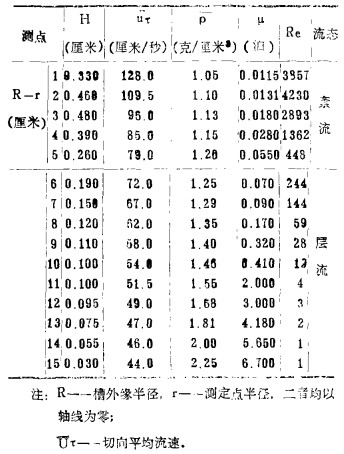
现有的研究表明,流态不同,支持矿群粒子悬浮的垂向力是不同的,研究两相流雷诺数,能较全面地揭示矿群床层松散的机理。在对矿浆流态的雷诺数进行研究时,必须对决定流态的相关物理量进行测定,作者采用相应的测定方法分别对矿浆流膜流速、矿浆粘度以及流膜厚度进行测定。当给矿体积为13升/分时测定结果如表 1及表 2所示。
| 表 1 螺旋溜槽两相流雷诺数沿径向的分布 |
 |
| 点击放大 |
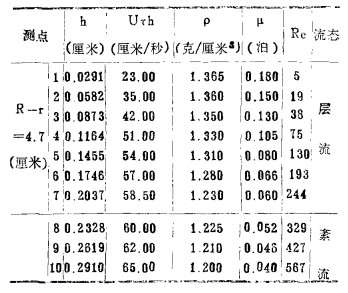
| 表 2 R-r=4.7厘米处雷诺数沿流膜厚度的分布 |
 |
| 点击放大 |
由实验得知,螺旋溜槽两相流雷诺数沿径向及流膜厚度的分布是不相同的,当变化给矿体积或外加离心力场时可以改变组成雷诺数的物理量,导致雷诺数变化。选别不同性质的矿物需要不同的流态,产生不同的升举力使颗粒悬浮分层达到分选目的。
二 一次环流及二次环流水流在螺旋溜槽中的运动是相当复杂的,在三个方向即沿流线方向、径向和流膜厚度方向都存在位变加速度,为了分析方便,人们把水流的运动分解为二个方向的运动,即沿切向的一次环流及沿径向的二次环流的运动。一次环流是由水的位能和离心力所产生的,主要决定于螺旋溜槽的结构参数,在分选中一次环流对矿石的搬运和分层起着主要作用,同时是二次环流产生的主要原因。
二次环流的产生,一般认为是由于水流的切向速度沿流膜厚度的分布不均匀引起离心力不同所产生的。上层水流和下层水流的流速不相同,上层水流切向流速大,具有较大的离心力而被推向外缘,到外缘后,螺旋倾角变小,水流受到边界效应的作用,速变减慢,离心力减小而进入下层,下层水流速度慢,离心力小,在重力的作用下沿横断面方向流向内缘,而内缘水流要补充上层水流外移时而空下来的位置,则必然上升,从而形成连续的水流运动,即二次环流。在二次环流中,存在一个中性面,即二次环流速度的大小为零的面,在中性面以上的水流流向外缘,中性面以下的水流流向内缘,因此二次环流是围绕中性面作三维空间的复合螺旋线运动[1]。
二次环流对选别有很大的影响,它能把悬浮在中性面之上的脉石轻矿物推向外缘而变成尾矿;把沉降到中性面之下的重矿物推向内缘而成为精矿,从而提高选别效果。
一次环流的切向速度测定方法,是将流膜速度通过电解质及电极对转换成电信号,然后采用电子扫描的方法记录下来,其测量误差小于2.5%。经给定条件测出切向流速沿流膜厚度的分布,切向流速沿径向的分布,结果分别如图 1、图 2所示。
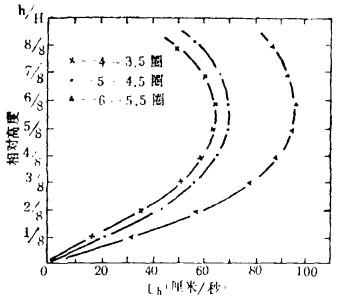 |
| 图 1 切向流速沿流膜厚度的分布 |
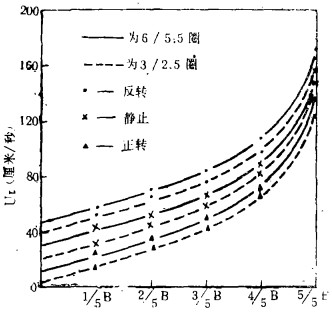 |
| 图 2 切向流速沿径向的分布 |
由图 1可以看出:切向速度Uτ沿流膜厚度的分布,表层快,底层慢,流膜层间存在速度梯度,这一特性在选别时具有意义,使颗粒受到剪切应力作用,其选别理论上面已作叙述。
由图 2可以看出:
1.切向速度Uτ随着转速的变化而变化,正转时,离心力增大,大量水流往外缘运动,槽的内缘及中间区流膜变薄,Uτ减小;反转时,流膜运动与正转的相反,Uτ增大;静止时,Uτ的大小居于正、反转流速之中。
2.切向流速Uτ随着离轴中心线的距离r的增大而增大,越往外缘,Uτ增大得越快,即Uτ沿径向存在速度梯度。
3.除了在溜槽外缘5/5B (B为测点上的槽宽)的测点之外,切向速度Uτ从上而下随着螺旋圈数的增加而增大,而测点5/5B处Uτ为最大,说明该处水流的紊动程度很大。
4.Uτ是决定流态雷诺数的相关物理量。
二次环流的存在是螺旋液流的一个特性,但是用肉眼是观察不到的,以前许多学者都作为假设来论述,由于现代测试技术的发展,现采用光学的方法将二次环流流动的矢量半定量地测出来。
三 流膜运动方程切向速度沿径向的分布,由于流速沿水层厚度存在速度梯度,现讨论的切向流速择其平均流速而言。苏联有人曾推导了螺旋选矿机平均流速公式[1],
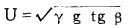
|
(4) |
式中:γ——水流质点至溜槽轴线的距离;
P——溜槽的螺旋角;
G——重力加速度。
(4) 式为大概沽计流膜切向速度提供了方便,但忽略了流转速的影响,而采用下式计算能反映实际。
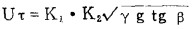
|
(5) |
式中:K1——流量系数,流量愈大,其值愈大;
K2——转速系数,正转速度愈大,则K2值愈小;反转速度愈大,则K2值愈大。
径向环流理论公式,由于切向流速和径向流速是互相影响和互相制约的,因此在推导过程中使用Burch C.R的假说[5],即先计算一次环流而不考虑二次环流,而后计算二次环流时,又认为它的存在不影响一次环流,这种假设是有一定意义的。在旋转螺旋溜槽中某一点,取定自然坐标系,切线τ, 主法线γ (径向),副法线h, 于流体中隔离出微元六面体,其边长分别为dτ、dγ、dh, 作用在此微元体上的力有重力、压力和摩擦阻力,如图 3所示。当微元体沿螺旋线运动时所产生的离心惯性力是与Uτh有关的,对旋转溜槽来说Uτh是一个相对值,应该根据速度合成定理求出微元体的绝对速度如图 4所示。经推导分别得到旋转螺旋溜槽正转时,反转时的径向环流公式(推导过程从略)[6]。
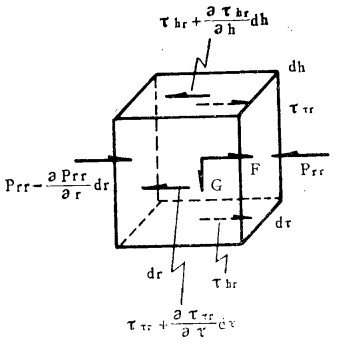 |
| 图 3 流体微元体受力分析 |
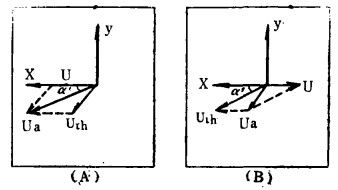 |
| 图 4 螺旋溜槽转动时微元体的速度合成 |
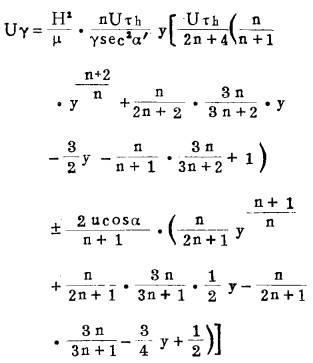
|
(6) |
式中,H——流膜总厚度;
μ——流体粘度;
n——表示流态的常数。
(6)式中±符号的决定,正转时取正号,反转时取负号。从(6)式可以看出,径向环流速度与表面切向流速、螺旋线的曲率半径、水的粘度、相对水层厚度及表示流态的n值有关。
现按测定数据进行计算比较,以R-r=4.7处(r=15.3厘米)为例,计算其表层(y=1)的径向环流速度,计算所需的数据列于表 3。
| 表 3 计算径向环流速度有关的测定数据 |
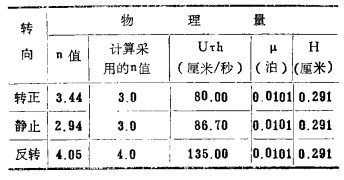 |
| 点击放大 |
1.分别计算静止,正转和反转时微远体绝对速度与水平线夹角,即α(静止)、α’(正转)和α’(反转)。
由tgα= L/2πγ,L(螺距)=24厘米,r=-15.3厘米。代入得
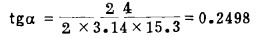
|
故α=14.03° cosα=0.970
由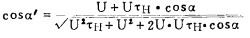
而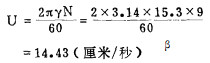
代入得:

|
同理可得: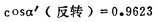
2.计算Ur正、Uor、Ur反
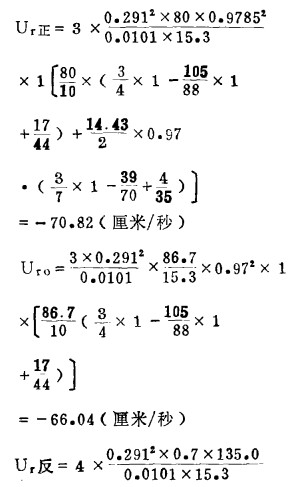
|

|
由上述计算可知,正转时径向环流速度大,反转时径向环流速度小,静止时居中,从而证实了关于加大流体的离心惯性力时径向环流加快,反之则径向环流减小的看法是正确的。同时可知,控制径向环流的大小,只要控制转速就可以达到。联系前面切向流速沿流膜厚度的分布可知,N变化,n亦变化,即流态变化。因此可知Uτ的变化引起流膜流态改变是完全可以的。
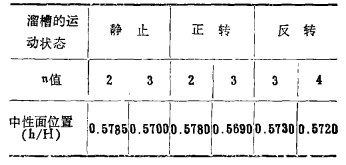
3.径向环流存在一个中性面,其径向速度为零,中性面的具体位置可以通过理论计算找到,经计算得到旋转螺旋溜槽正转、静止及反转时对径向环流中性面位置随n值的变化关系,列于表 4中。
| 表 4 中性面位置与n值的关系 |
 |
| 点击放大 |
由表 4可以看出:旋转螺旋溜槽正向转动时,中性面下降,反向转动时中性面上升,且其上升、下降的大小与溜槽转动速度及流态n值有关,中性面在流膜中的这一运动规律对选矿具有重要意义。正转时,中性面往重矿物品位更高的方向移动,即中性面降低,因此重矿物的质量就会提高,但回收率会下降;反转时则会出现相反的情况,应该指出,溜槽正、反转均存在临界转速。
4.离心流场质点运动轨迹。上述讨论的径向环流是一个理想的流动面,但实际流场中质点运动轨迹是由螺旋线运动的切向速度。径向环流速度和重力下滑速度的合成运动,也就是流体质点的径向环流围绕中性面作三维空间复合螺旋线运动如图 5所示。流场质点运动速度为:
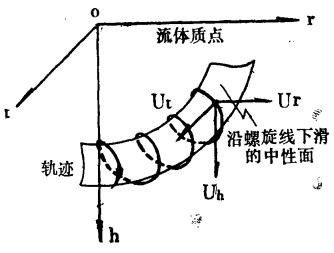 |
| 图 5 质点的运动轨迹 |
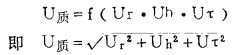
|
(7) |
其中Uh可视为不可压缩单位重量的理想流体作稳定绝对运动时的速度,由伯努利方程求得:
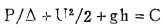
|
(8) |
式中:P——流体静压力;
A——流体密度;
U——流体运动速度;
h——流体质点运动高差;
C——积分参数。
流体质点空间运动轨迹方程为:
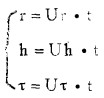
|
(9) |
式中:r、h、τ分别为流体质点与取定的自然坐标轴系的距离。
流场质点方向可由U质与坐标轴所构成夹角的方向余弦求得[3]:
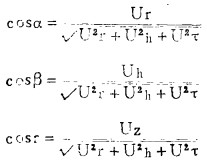
|
(10) |
式中:α、β、r分别为质点运动方向与r、h和τ轴的夹角。
四 回收粒级的理论计算螺旋溜槽选别钒钛磁铁矿时,粒级回收的理论计算,在此仅选取靠近溜槽外缘的一点(R-r=4.7厘米)对矿粒回收情况进行分析[7]。
从测定及计算结果知:在R-r=4.7厘米处,其h=0~0.75H区间内液流雷诺数为Re < 300, 即流态为层流,因此只能是分散压P促使床层松散,矿粒在纵断面上的受力情况如图 6所示。
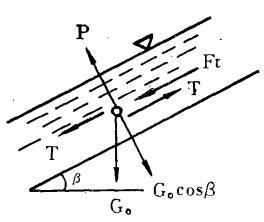 |
| 图 6 矿粒在溜槽纵断面的受力分析 |
矿粒在水中受到的重力沿垂直于剪切方向的分力:
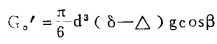
|
(11) |
式中:d——矿粒直径;
δ——矿粒密度;
Δ——水的密度;
β——溜槽的螺旋角。
设直径为d的矿粒所受到的分散压力为:P•π/4•d2,要使矿粒悬浮,必须满足:
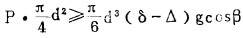
|
(12) |
借用二次环流速度计算式求得:中性面在h=0.578~0.579H区间内。因悬浮于中性面上、下两侧的矿粒,其径向运动方向相反,故取其上、下两点予以计算。
1.取h=0.5H时,则矿浆浓度为33%,(μ=0.028泊,容积浓度为C’=0.11,C'*为颗粒静态堆置时的最大容积浓度,一般圆滑而均匀的颗粒取C‘*=0.65。
矿浆线性浓度由下式计算:
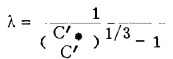
|
(13) |
分别将C'、C'*、代入(13)式计算得λ=1.24。
计算流速梯度可采用下式:
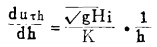
|
(14) |
式中: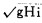
i——水力坡度;
h——距床底高度;
k——尔曼常数,取k = 0.34。
由(14)式计算得duih/dh = 171(1/秒)。又给矿最大粒度dmax=0.0074厘米,由拜格诺德判定准数公式:
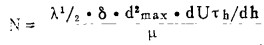
|
(15) |
得N=0.99
因N=0.99 < 40, 故属粘性剪切。
代入计算分散压公式:
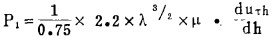
|
(16) |
得P1=19.40(达因/厘米2)
2.取h=0.6H时,同理可以计算分散压为:
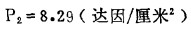
|
又令(12)式中的P•π/4•d2=P’d;
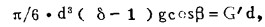
|
分别对不同直径的矿粒所受的分散压计算结果列于表 5。
| 表 5 矿粒受力计算结果 |
 |
| 点击放大 |
根据(12)式的悬浮条件及表 5可以看出,二次环流中性面以上h=0.6H处,则有G'0.00.0(长石)↑ < P‘0.0020 > G'0.0020 (钒钛磁铁矿)↑二次环流中性面以下h=0.5H处,则有G’0.0074(长石)↑ > P‘0.0074 > G'0.0074(钒钛磁铁矿)↓即20微米的长石及钒钛磁铁矿均能悬浮,不可能沉降通过中性面,只能由二次环流带向外缘作为尾矿排出,致使细粒有用矿物损失于尾矿;74微米的长石能悬浮,而钒钛磁铁矿能沉降通过中性面,被二次环流送回内缘精矿区,最终作为精矿回收。
由(12)式可以求钒钛磁铁矿通过中性面的最小粒度,即回收粒度下限dmin为
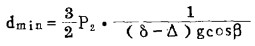
|
(17) |
将P2=8.29(达因/厘米2),δ=5.2(克/厘米3),△=1(克/厘米3),代入(17)式得dmin=0.0031厘米=31微米。
同理可以计算在螺旋溜槽R-r =8.7厘米处矿粒回收粒度下限dmin=0.0027厘米=27微米。
上述矿粒的受力分析,是从流态不同所受作用力亦异的观点出发进行计算的,计算结果与实验回收粒度下限是一致的。
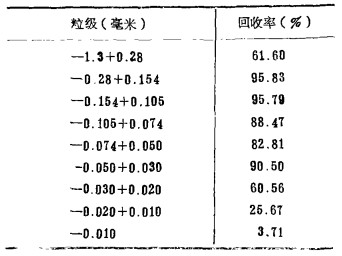
3.粒级回收下限实例之一。某矿采用浮选法选别硫化锑,其尾矿中含有氧化锑,现厂采用摇床来回收,由于浮选尾矿含泥量大,粒度细,故回收率低。经采用旋转塔形螺旋溜槽来回收氧化锑,半工业性试验表明是可行的,其粒级回收率如表 6所示。
| 表 6 粒级回收率 |
 |
| 点击放大 |
由表 6可以看出,回收细粒氧化锑矿-30+20微米的粒级还可以回收60.56%,此一粒级回收下限与理论计算回收粒级下限是相一致的,从而证实理论计算是符合实际的。
五 结论1.研究螺旋溜槽两相流雷诺数分布的规律能揭示分选机理,在层流流态中,矿粒的松散和悬浮主要靠颗粒相互剪切所产生的分散压,在紊流流态中主要靠紊动压力使床层松散,引起矿粒析离分层。不同的流态,产生不同的升举力使矿粒悬浮分层达到分选的目的。
2.对旋转螺旋溜槽进行流膜速度分布特性的研究,结果表明:槽面上不同半径之处切向流速沿流膜厚度的分布,切向流速沿径向的分布以及流态均是不相同的。
3.分别探讨了旋转螺旋溜槽的一次环流切向流速及二次环流流速的表达式。通过计算可以得出溜槽正转、反转及静态的二次环流速度,通过控制二次环流速度大小及中性面位置的高低,对选矿具有重要意义。
4.推导了溜槽中流场质点三维空间运动轨迹方程。
5.通过回收粒级的计算,得知某测定回收粒级下限与实际测定相一致。
| [1] |
〔苏〕M. Ф阿尼金等著: 《螺旋选矿机》, 冶金工业出版社, 1975年6月
|
| [2] |
R. O. Burt, spiral concentration Current trends in design and oieraticm《 Mineral processing and Extractive Metallurgy》, editors M. J. Jones and P. Gill IMM, 1984, England, P. 117—127
|
| [3] |
李富成主编: 《流体力学及流体机械》, 冶金工业出版社, 1980年1月
|
| [4] |
R. A. Bagnold, "Experiments on a gravityfree dispersioa ot large solid spheres iu a newtonian fluit under shear", 《Proceedings of the Royal society》, A. 1954, NO 1160, vol. 225, P49—63
|
| [5] |
卢继美, 等. 螺旋选矿机中水流的运动规律[J].
《有色金属》(选矿部分), 1980(4).
|
| [6] |
徐镜潜, 等. 离心螺旋溜槽流膜特性的研究[J].
《有色金属》(季刊), 1983(2).
|
| [7] |
徐镜潜, 等. 两相流雷诺数的研究[J].
《有色金属》(季刊), 1982(3).
|
 1987, Vol. 1
1987, Vol. 1
