江西有色金属  1987, Vol. 1 Issue (2): 49-56
文章快速检索     高级检索
引用本文
0
邓佐国, 徐廷华. 铕钆萃取分离的动态平衡计算及程序编制[J]. 江西有色金属, 1987, 1(2): 49-56.
铕钆萃取分离的动态平衡计算及程序编制[PDF全文]
邓佐国 , 徐廷华     
江西冶金学院
摘要：本文用FORTRAN语言编制了应用电子计算机技术完全模拟"分液漏斗法"的实验澡作，对皂化P507盐酸体系的Eu/Gd分离进行了动态平衡计算。得到了人工实验中无法获得的信息和结论。本程序不仅适用于Eu/Gd分离，而且也适用于任一恒定混合萃取比体系的双组份分离。
${affiVo.addressStrEn}

一 概述

铕钆是化学性质相似，分离因数较小的难分离元素对，需要的萃取级数很多。用分液漏斗进行串级萃取模拟实验，需要长时间才能达到预期的结果和体系的平衡，极为费工耗时。本文在北京大学串级萃取理论〔1-5〕研究的基础上，用FORTRAN语言编制了用电子计算机模拟“分液漏斗法”的实验操作的计算程序。对铕钆的串级萃取从启动到稳态进行逐级逐排的计算，即进行所谓的串级萃取动态平衡的计算。计算机技术代替人工实验，不仅节约时间，而且能快速、确准地获得串级萃取过程中的大量信息，这是人工实验无法实现的。本程序不仅适用于(Eu3+、Gd3+)/HC/皂化P507—磺化煤油(RA3·3 HA)体系，也适用于一切恒定混合萃取比体系的双组份分离。它是研究与设计优化串级萃取工艺的有力工具。

二 程序编制

1.静态工艺参数设计  我国科技工作者在应用P507萃取分离提纯稀土元素方面做了大量工作，取得了可喜的成绩〔6-8〕。本研究是以江西寻乌稀土经P204萃取分组的中稀土，在P507盐酸体系中进行Sm/Eu及Gd/Tb分离后〔9〕，所得的铕钆富集物为原料进行铕钆分离。

铕轧分离是以水相进料的二元体系。其中FA=FGd=0.826，FB=FEu=0.174。

为了保证Gd2O3有较高的纯度和收率，拟定的分离指标为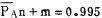：，YA=1099，选取βGd/Eu=1.5。

根据串级萃取理论Ⅰ1Ⅳ对本体系的静态工艺参数：W(洗涤量)、S(萃取量)、E'M(萃取段的混合萃取比)，E'M(洗涤段的混合萃取比)，N(萃取段级数)，M(洗涤段级数)进行计算。

由水相进料的极值公式有：

假设进料MF=1.00毫克分子，在极值范围内计算了K=0.50~0.95共10组可供选择的工艺参数，选取R=S(N+M)最小的一组(K=0.70)的工艺参数：

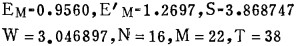
进行串级萃取动态平衡计算(考虑到生产实际，将级数增加五级)。

2.串级萃取的计算机模拟  根据串级萃取理论Ⅵ〔5〕中两组份体系的萃取平衡方程，及计算机对串级模拟实验中的启动前的充料、摇振、相转移，加料和排料等动作的计算机模拟。用FORTRAN语言編制了程序，并在微机上对铕钆萃取分离进行了动态平衡计算。

铕钆萃取分离动态平衡计算程序

A..B# T

       REAL MA(2, 52), MB(2, 52), MT(2, 52)

       DIMENSION XA(2, 52), XB(2, 52), YA(2, 52), YB(2, 52), XAP(52), (52),

  1    YAP (52), YBP(52), XA 1(1, 52), XA 2(1, 52)

       DATA XA/104*0.0/, XB/104*0.0/, YA/104*0.0/, YB/104*0.0/

  1    XBP/52*0.0/, XAP/52*0.0/, YAP/52*0.0/, YBP/52*0.0/

       DATA N, M/20, 23/, S, W, FAI, FBI/3.86876, 3.04691, 0.8218, 0.1782/,

  1    FA, FB, BATA, BATA1, PB, PA/0.826, 0.174, 2*1.5, 0.96, 0.995/

       D(A, B, C)=SQRT(B*B-4.0*A*C)

       ROOT(A, B, C)=(-B + D(A, B, C)/(2.0*A)

       G=FLOAT(N + M)

       N1=N + 1

       N2=N + 2

       N3=N + 3

       N4=N + M - 1

       N5=N+M

       N6=N + M + 1

       N7=N + M + 2

       DO 1 I=1, 2

       DO 1 J=1, N 7

       MA(I, J)=0.0

  1    MB(I, J)=0.0

       MA(1, 2)=(S + FB1)*FA

       DO 5, J=4, N, 2

  5    MA(1, J)=(S + W + 1.0)*FA

       DO 2 J=N2, N4, 2

  2    MA(1, J)=(S+W)*FA

       MA(1, N6)=(W + FA1)*FA

       MB(1, 2)=(S + FB1)*FB

       DO 3 J=4, N, 2

  3    MB(1, J)=(S + W + 1.0)*FB

       DO 4 J=N2, N4, 2

  4    MB(1, J)=(S+W)*FB

       MB(1.N6)=(W + FA1)*FB

       WRITE(3, 110)(J, MA(1, J), J=2, N6)

  110  FORMAT(1X, 4(’M A(1, ’I2, ’)=’, F8.6, 2X)

       WRITE(3, 111)(J, MB(1, J), J=2, N6)

  111  FORMAT(1X, 4 (’MB(1, ’, )12, ’)=’, F8.6, 2X)

       I=0

  150  I=I+1

       DO 8 J=1, N6, 1

  8    MT(1, J)=MA(1, J)+MB(1, J)

       IF ((FLOAT(I)/2.0-I/2), EQ.0.0)GOTO 135

       DO 9 J=2, N, 2

       A1=BATA-1.0

       B1=(BATA-1.0)*(S-MA(1, J))+MT(1, J)

       C1=(S-MT(1, J))*MT(1, J)*MA(1, J)

       XA1(1, J)=ROOT(A1, B1, C1)

       XA2(1, J)=XA1(1, J)-D(A1, B1, C1)/A1

       IF(XA1(1, J).LT.MA (1, J).AND. XA1(1, J).GT.0.0) XA(1, J)=XA1(1, J)

       IF(XA2(1, J).LT.MA (1, J).AND. XA2(1, J).GT.0.0) XA(1, J)=XA2(1, J)

       YA(1, J)=MA(1, J)-XA(1, J)

       YB(1, J)=S-YA(1, J)

       XB(1, J)=MB(1, J)-YB(1, J)

  9    CONTINUE

       DO 10 J=N2, N6, 2

       A2=BATA1-1.0

       B2=(1.0-BATA1)*W+(BATA1-1.0)*MB(1, J)+ MT(1, J)

       C2=(-W*MA(1, J))

       XA1(1, J)=ROOT(A2, B2, C2)

       XA2(1, J)=XA1(1, J)-D(A2, B2, C2)/A2

       IF(XA1(1, J).LT.MA(1, J).AND. XA1(1, J).GT.0.0)XA(1, J)=XA(1, J)

       IF(XA2(1, J).LT.MA(1, J).AND. XA2(1, J)GT.0.0)XA(1, J)=XA2(1, J)

       XB(1, J)=W-XA(1, J)

       YA(1, J)=MA(1, J)-XA(1, J)

       YB(1, J)=MB(1, J)-XB(1, J)

  10   CONTINUE

       GOTO 1>0

  135  DO 18 J=3, N1, 2

       A1=BATA-1.0

       B1=(BATA-1.0)*(S-MA(1, J))+MT(1, J)

       C1=(S-MT(1, J))*MA(1, J)

       XA1(1, J)=ROOT(A1, B1, C1)

       XA2(1, J)=XA1(1, J)-D(A1, B1, C1)/A1

       IF(XA1(1, J).LT.MA(1, j).AND

  XA1(1, J).GT.0.0) XA(1, J)-XA1(1, J)

       IF(XA2(1, J).LT.MA(1, J).AND

  XA2(1, J).GT.0.0)XA(1, J)=XA2(1, J)

       YA(1, J)=MA(1, J)-XA(1, J)

       YB(1, J)=S-YA(1, J)

       XB(1, J)=MB(1, J)-YB(1, J)

  18   CONTINUE

       DO 19 J=N3, N5, 2

       A2=BATA1-1.0

       B2=(1.0-BATA1)*W+(BATA1-1.0)*MB(1, J)+MT(1, J)

       C2=(-W*MA(1, J))XA1(1, J)

       XA1=ROOT(A2, B2, C2)

       XA2(1, J)=XA1(1, J)-D(A2, B2, C2)/A2

       IF(XA1(1, J).LT.MA(1, J).AND.XA1(1, J).GT.0.0) XA(1, J)=XA1(1, J)

       IF(XA2(1, J).LT.MA(1, J).AND.XA2(1, J).GT.0, 0) XA(1, J)=XA2(1, J)

       XB(1, J)=W-XA(1, J)

       YA(1, J)=MA(1, J)-XA(1, J)

       YB(1, J)=MB(1, J)-XB(1, J)

  19   CONTINUE

       DO 11 J=2, N6, 1

       YAP(J)=YA(1, J)/(YA(1, J)+YB(1, J))

       YBP(J)=1.0-YAP(J)

       XBP(J)=XD(1, J)/(XB(1, J)+XA(1, J))

       XAP(J)=1.0-XBP(J)

  11   CONTINUE

       WRITE(3, 102)(J, YAP(J), J=2, N6)

  102  FORMAT (1X, 5(’YAP(’, I2’, )=’, F7.6, 1X))

       WRITE(3, 106)(J, YBP(J), J=2, N6)

  106  FORMAT(1X, 5(’YBP(’, 12, ’)=’, F7.6, 1X))

       WRITE(3, 107)(J, XBP(J), J=2, N6)

  107  FORMAT(1X, 5(’XBP(’, 12, ’)=’, F7.6, 1X))

       WRITE(3, 108)(J, XAP(J), J=2, N6)

  108  FORMAT(1X, 5(’XAP(’, 12, ’)=’, F7.6, 1X))

       II=I/2

       XBNP=XB(1, N1)/(XB(1, N1)+XA(1, N1))

       XANP=1.0-XBNP

       AW=(XA(1, 2)+YA(1, N6))/FA

       BW=(XB(1, 2)+YB(1, N6))/FB

       SUM1=0.0

       SUM2=0.0

       DO 12 J=2.N1, 1

       SUM1=SUM1+MA(1, J)

  12   SUM2=SUM2+MB(1, J)

       TSA=SUM1/N

       TSB=SUM2/N

       SUM3=0.0

       SUM4=0.0

       DO 13 J=N2, N6, 1

       SUM3=SUM3+MA(1, J)

  13   SUM4=SUM4+MB(1, J)

       TWA=SUM3/M

       TWB=SUM4/M

       SUM5=SUM1+SUM3

       SUM6=SUM2+SUM4

       TMA=SUM5/G

       TMB=SUM6/G

       WRITE(3, 103)II, XBNP, XANP, AW, BW, TSA, TSB, TWA, TWB, TMA, TMB

  103  FORMAT(1X’ II=’, 15, 2X, ’XBNP=’, F7.6, 2X, ’XANP=’, F7.6, 2X, ’AW=’, F8.6

    1  2X, ’BW=’, F8.6, 2X, ’TSA=’, F8.6’1X, ’TSB=’, F8.6, 3X, ’TWA=’, F8.6,

    1  3X, ’TWB=’, F8.6, 3X, ’TMA=’, F8.6, 3X, ’TMB=’, F8.6)

  170  DO 14 J=2, N6, 1

  14   MB(2, J)=XB(1, J+1)+YB(1, J-1)

       DO 16 J=2, N6, 1

  16   MA(2, J)=XA(1, J+1)+YA(1, J-1)

       IF((FLOAT(I)/2.0-I/2).EQ.0.0) GOTO 300

       B1P=XBP(2)

       IF(B1P.LT.PB) GOTO200 I1=(I+1)/2

       GB=FLOAT(I1)/G

       WRITE(3, 104) I1, GB, B1P

  104  FORMAT(1X, ’I1=’, I6.5X, ’GB=’, F8.2, 5X, ’B1P=’, F7.6)

       IF(ABS(1.0-AW).LE.1.OE-5.AND ABS(1.0-BW). LE.1.OE-5)STOP

  200  IF(FLOAT(N)/2.0-N/2).NE.0.0)GOTO 250

       MA(2, N1)=MA(2, N1)+FA

       MB(2, N1)=MB(2, N1)+FB

       IF((FLOAT(M)/2.0-M/2).NE.0.0) GOTO 310

  270  DO 15 J=2, N6, 1

  15   MB(1, J)=MB(2, J)

       DO 17 J=2, N6, 1

  17   MA(1, J)=MA(2, J)

       GOTO 150

  250  IF((FLOAT(M)/2.0-M/2).NE.0.0) GOTO 270

  310  ANMP=YAP(N6)

       IF(ANMP.LT.PA)GOTO 270

       IF(FLOAT(I)/2.0-I/2).EQ.0.0) I2=I/2

       IF((FLOAT(I)/2.0-I/2).NE.0.0) I2=(I+1)/2

       GA=FLOAT(I2)/G

       WRITE(3, 105) I2, GA, ANMP

  105  FORMAT(1X, ’I2=, ’I6, 5X, ’GA=’, F8.2, 5X, ’ANTMP=’, F7.6)

       IF(ABS(1.0-AW).LE.1.OE-5.AND. ABS(1.0-BW).LE.1.OE-5) STOP

       GOTO 270

  300  IF((FLOAT(N)/2.0-N/2).EQ.0.0) GOTO 350

       MA(2, N1)=MA(2, N1)+FA

       MB(2, N1)=MB(2, N1)+FB

       IF((FLOAT(M)/2.0-M/2)EQ.0.0) GOTO 270

       GOTO 310

  350  IF((FLOAT(M)/2.0-M/2).NE.0.0) GOTO 270

       GOTO 310

       END

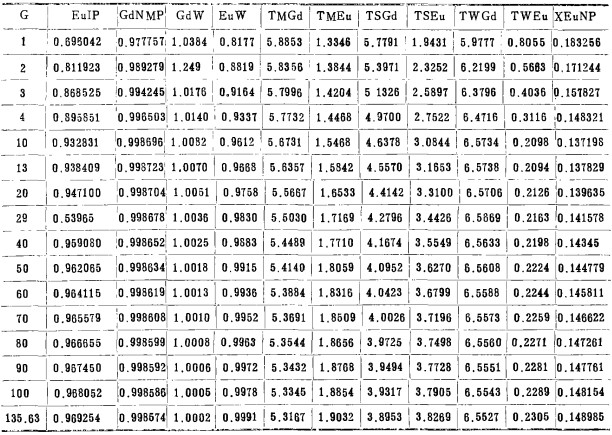
三 计算结果分析与讨论

1.计算结果  串级萃取的动态平衡过程，是铕、钆组份在串级萃取中不断重新分布的过程。也是铕、钆组份逐渐积累或排放的过程。各动态参量随排级比G的变化而变化。计算结果列于表 1和图 1—4中(表2略)

表 1 串级萃取动态平衡计算结果
点击放大

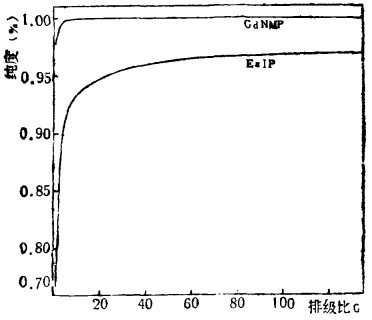图 1 出口产品纯度与排级比的关系

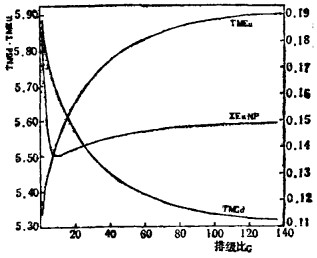图 2 TMGd、TMEu、XEuNP与排级比G的关系

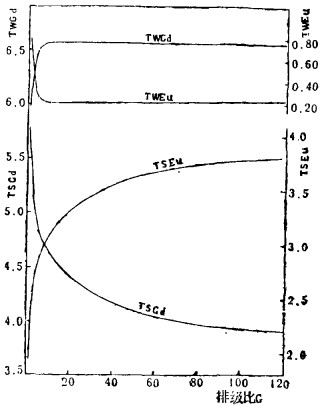图 3 TSGd、TSEu、TWGd、TWEu与排级比G的关系

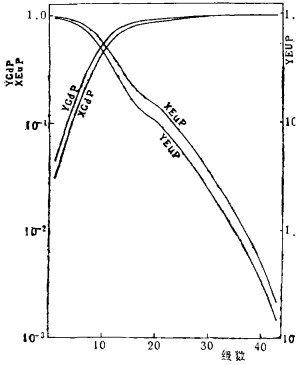图 4 Gd、Eu在各级的纯度分布

2.计算结果分析与讨论

(1) 由表 1和图 1可见，两相出口产品纯度Eu1P和GdNMP，总的趋向是随排级比G的增加而提高，并在GA, GB处分别达到分离指标，最后达到平衡。Eu和Gd谁先达到预定分离指标，与原料组成有关。本研究所采用的铕钆富集物中钆的含量(fGd=0.826)比铕的含量(fEu=0.174)高得多。故当排级比GA=4.0，即摇到172排时，Gd的纯度达到分离指标(GdNMP= 0.995)。而铕在排级比GB=29，即摇到1247排时，Eu的纯度才达到分离指标(Eu1P=0.9536)。达到平衡后。Eu1P和GdNMP在一定数值范围内不再变化，平衡度GdW和EuW分别趋近于1。

Eu1P随G的变化呈单调上升，而GdNMP在(GA)max=13.0处有极大值。这与料液中Gd的含量较高有关。

(2) 由计算结果可估计达到纯度指标所需的最少时间DA、DB。若“漏斗法”的操作一天能摇20排，由表 1及图 1中可查到GA=4.0，GB=29，则

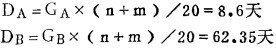
所以两相出口同时满足产品纯度要求所需最少时间为62.35天。

若以铕的平衡度(Euw)达99.91%为该体系基本达到平衡的指标，由表 1査知，GAB=135.63，则DAB=GAB×(n+m)/20=291.6天 所以用漏斗实验是难以使体系达到稳态的，只有生产上长期运转才有可能。

应用以上数据及根据相接触时间，澄清室与混合室的体积比，也可估计混合澄清槽操作时，达到稳态所需的时间或任一时间内两相出口产品的纯度。

(3) 由表2 (略)图 4可见，第18级水相组成与料液组成最接近，这一级可定为实验或生产的进料级。

(4) 由图 2及表 1可见，在串级萃取过程中，Gd随排级比G的增加而不断排放，Eu随G的增加而不断积累。图 3可见，萃取段的TSEu随G的增加而不断积累，TSGd随G的增加而不断排放。洗涤段的TWEu随G的增加而不断排放，TWGd随G的增加而不断积累。这是因为在萃取段出口水相获得纯Eu产品，即Eu必须从料液中的0.174富集到0.9536，故在萃取段Eu必定是积累的，反之，洗涤段的出口有机相获纯Gd产品，所以Gd在洗涤段必定是积累的。

(5) 由图 4及表2(略)可知，两相出口产品均已超过预定指标，洗涤段有4级富余，萃取段有1级富余。因比该工艺条件是可行的，可按此条件进行试验或生产，只是将洗涤段级数适当减少即可。可见，电子计算机技术不仅可代替费时耗工的串级模拟试验产生萃取工艺条件，而且可检验现行生产上的串级萃取工艺条件是否合理。

(6) 由于计算中排除了实验中可能造成的各种误差因素，故该计算称为“理想的实验操作”。目前至少可以做到，用计算机技术确定串级萃取工艺条件，再用实验验证，避免盲目性。这对串级萃取实验及生产都有极大的指导意义。

(7) 本文用FORTRAN语言编制的程序，不仅适用于Eu、Gd分离，也适用于任一恒定混合萃取比体系的双组份分离。

为了节省篇幅，文中符号意义，请参阅文献〔1-5〕

参考文献
[1]
徐光宪: 《北京大学学报》, 1978年, 第1期, 51页
[2]
徐光宪: 《北京大学学报》, 1978年, 第1期, 67页
[3]
李标国、徐献瑜、徐光宪: 《北京大学学报》, 1980, 第2期, 66页
[4]
徐光宪、李标国、倪亚明: 《稀有金属》, 1982年, 第1期、10页
[5]
李标国、李俊然、严能华、徐光宪: 《稀有金属》, 1985年第3期
[6]
北京有色院: P507盐酸体系萃取分离包头矿稀土的研究, 1980年
[7]
包头冶金研究所: P507盐酸体系轻中稀土全萃取连续分离小试报告1981年
[8]
包头冶金研究所: P507盐酸体系轻中稀土全萃取连续分离工艺扩大试验报告, 1982年
[9]
邓佐国: P507盐酸体系全萃取连续分离江西寻乌中稀土工艺流程研究(一), 《江西冶院科技》1984年, 第1期