国家教育部主管、北京师范大学主办。
文章信息
- 张婕, 黄碧娟, 司继伟, 官冬晓. 2018.
- ZHANG Jie, HUANG Bijuan, SI Jiwei, GUAN Dongxiao. 2018.
- 乡镇小学生的数学焦虑与数学成绩:数学自我效能感和数学元认知的链式中介作用
- Relationship between Math Anxiety and Mathematical Achievement in Township Pupils: The Chain Mediating Roles of Mathematical Self-efficacy and Metacognition
- 心理发展与教育, 34(4): 453-460
- Psychological Development and Education, 34(4): 453-460.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2018.04.09
数学是一门极其重要的工具学科,占据着学生从幼儿园到大学乃至更高层次的学习生活。美国国家研究理事会1989年曾提出,拥有数学和几何领域的基础,对所有职业的专业化都至关重要,很多国家正在深入开展数学课程的改革,以使得数学教育更符合人学习的心理活动发展规律。许多研究聚焦于影响数学成绩的因素,以及如何提高和数学相关的技能、策略,进而为相应的数学课程改革提供依据。影响数学成绩的因素包括与学生数学学习相对紧密的个人因素(如数学焦虑、数学学习效能感和数学元认知等)和环境因素(如数学课的负面经验和数学老师的支持等) (Eysenck & Calvo, 1992; Guay, Marsh, & Boivin, 2003; Lee, Lee, & Bong, 2014)。目前,大多数研究仅仅针对其中的一、两个变量进行探索,并未能系统地、全面地描述影响数学成绩的内在机制。因此,从个体因素和环境因素等多方面,同时分析多个变量对数学成绩的影响,将能更全面深刻地了解和揭示数学成就个体差异的成因机制,为数学课程改革和数学教学提供理论支持。
1.1 数学焦虑与数学成绩数学焦虑,作为特殊的学科焦虑之一,是普遍存在的带有认知色彩的消极情绪,其相关研究可追溯到上世纪50年代(司继伟, 徐艳丽, 封洪敏, 许晓华, 周超, 2014)。数学焦虑被认为是一种不舒服的数学任务表现状态,即在处理数字、使用数学概念、学习数学知识、解决数学问题等时所产生的不安、紧张、畏惧、担忧等焦虑体验,在各种普通生活和学术情景中它被定义为干扰数字操纵和解决数学问题的紧张和焦虑感(Carey, Hill, Devine, & Szücs, 2016; 崔吉芳, 李嫩晓, 陈英和, 2011),从而对数学成绩产生明显不良影响(Devine, Fawcett, Szücs, & Dowker, 2012; Jansen, 2008)。学生能力国际评估计划(Programme for International Student Assessment, PISA)是目前全球最权威的学习素养测试之一,旨在评估不同地区15岁学生在阅读、数学及自然科学方面的知识、能力和技巧,以及跨学科的基础技能,在2012年PISA以数学素养为主要评价领域,足可见个体的数学素养在当下社会的重要性(刘星辰, 原露, 陈启山, 2016)。此外,从社会认知角度出发,成功的职业道路包括个体追求事业的能力和运用这种能力的动机,而如果不擅长数学和科学,就很难从事与STEM (Science, Technology, Engineering, and Mathematics)相关的活动,更不用说从事STEM职业(Wang & Degol, 2017)。因此,数学焦虑不仅会影响个体的学业成绩、甚至会影响到其后续的专业和职业选择,因而成为数学教育、数学认知等领域的研究焦点之一。
1.2 数学焦虑和数学自我效能感、数学成绩的关系数学自我效能感是自我效能感在数学领域的具体化,一般指个体对自己解决特定数学问题,执行数学相关的任务,或者在数学相关的课程中取得成功的能力的判断(庄鸿娟, 刘儒德, 刘颖, 2016)。数学自我效能感受很多因素影响,如数学焦虑、消极认知等。已有研究发现,数学自我效能感影响着学生行为的选择、努力、面对任务时的坚持性以及做事时的思维方式和情绪反应,高的自我效能感能使学生在解决问题时表现较高的兴趣和注意,提高努力水平,在遇到困难时有较高的坚持性,越来越多的研究结果支持效能感的预测作用和中介作用(孔令跃, 2002)。根据干扰模型理论,高低数学焦虑学生的成绩差异主要是由注意集中的差异引起的,评价情境中的各种思维如担忧、消极自我集中、自卑体验等认知导致的,从而学生自我效能感的高低中介了数学焦虑与成绩(张宁, 2006)。
目前,关于自我效能与学业成就之间联系的研究主要集中在学生的自我效能感是如何影响学业表现的(Bernacki, Nokes, & Aleven, 2014; Singh, Granville, & Dika, 2002; Stake, 2010)。有证据表明,自我效能感可直接影响数学表现(Xu & Jang, 2017)。Shams, Mooghali, Tabebordbar和Soleimanpour (2011)报告了在数学学习领域,具有强烈数学自我效能感的学生往往在数学计算中表现出很高的准确性,并在困难的数学任务上比低数学自我效能的学生更能坚持。Derakshan等(2009)也表明,数学中的自我效能与数学焦虑呈负相关,并与数学成绩呈正相关。这些发现意味着,数学自我效能感、数学焦虑和数学成绩三者间存在一定的关系。因此,研究假设数学自我效能感可能在数学焦虑和数学成绩间起中介作用。
1.3 数学焦虑和数学元认知、数学成绩的关系元认知是指“反思、理解和控制学习的能力” (Schraw & Dennison, 1994)。数学元认知,即在数学学习中,个体对数学认知活动的自我意识和自我监控,它以元认知知识为基础,并在对数学认知过程的评价、控制和调节中显示出来,对数学认知过程发挥知晓、支配、决策、监控的作用(申继亮, 陈英和, 2014)。
许多研究者探讨了数学元认知对数学问题解决的影响,发现3、4年级儿童的元认知与其问题解决能力有很强的相关,元认知能力可以被训练以提高应用题解题能力(Jacobse & Harskamp, 2012)。近期研究还发现数学元认知和数学焦虑是与数学成绩和数学问题解决相关的重要认知和情感变量,低数学焦虑学生使用更多元认知调节(Lai, Zhu, Chen, & Li, 2015)。在信息加工之前,高数学焦虑的个体可以通过回避与数学相关的情境来影响数学学习(Chinn, 2009)。随后在信息加工和检索阶段,数学焦虑可能通过认知干预来影响数学表现,如会占用工作记忆资源,而工作记忆资源对于加工和检索数学事实和方法至关重要(Ashcraft & Krause, 2007; Krinzinger, Kaufmann, & Willmes, 2009)。抑制型焦虑模型理论(the Debilitating Anxiety Model)则认为,数学焦虑会通过影响信息的预加工、加工和检索,占用元认知资源,降低个体的数学表现(Carey et al., 2016),即为数学元认知在数学焦虑和数学成绩之间起中介作用提供理论依据。国内有关研究也已证实,数学元认知在数学焦虑和数学成绩之间起中介作用(周双珠, 韩瑽瑽, 陈英和, 2014)。但对于数学元认知的中介作用仍然需要更多实证研究证据进行支持。
1.4 数学焦虑、数学自我效能感、数学元认知和数学成绩的关系大量实证研究已发现,数学焦虑和数学成绩存在显著负相关关系(Ashcraft & Krause, 2007; Devine et al., 2012; Jansen et al., 2013)。因此,数学焦虑影响数学成绩的作用机制颇受研究者关注。干扰模型理论为数学自我效能感在数学焦虑和数学成绩之间起中介作用提供了理论依据,抑制型焦虑模型理论则为数学元认知在数学焦虑和数学成绩之间起中介作用提供了理论依据。以上两种理论表明,数学自我效能感、数学元认知在数学焦虑与数学成绩的关系间起着重要作用。
此外,数学自我效能感和数学元认知之间也存在密切联系。Pennequin等人(2010)曾提出,受效能信念控制的各种心理社会过程与认知能力的培养都有密切的关系,通常在寻找解决方案时,高自我效能感的学生往往表现出高度的灵活性,而他们在评估自己智力表现的质量时也更为准确。相关研究发现低焦虑水平且更积极自信的学生会通过增加毅力、策略和认知资源的补充提高学习表现(Sabourin & Lester, 2014; Verkijika & De Wet, 2015)。不仅如此,自我效能感与个体对元认知策略的运用存在直接关系,对数学没有焦虑、恐惧和厌恶等情绪反应,数学自我效能感高的学习者会更好地运用元认知策略以产生成功的数学表现(Hoffman & Spatariu, 2007)。Horn等人(1993)曾发现自我效能感对元认知策略使用的数量和类型产生了积极的影响。因此,自我效能感能通过影响元认知策略的使用来影响个体的学业表现,自我效能感的提高会形成元认知策略自动化,从而获得更好表现。胡桂英和许百华(2003)也指出,自我效能感可能是通过影响学习策略的使用间接影响学业成绩。根据抑制型焦虑模型,焦虑、恐惧和担忧会打击学生在数学任务上的自信心,降低数学自我效能感,进而影响他们在数学情境下认知策略的选择,抑制元认知资源的使用,最终降低学习表现(Chinn, 2009; Devine et al., 2012; Jansen, 2008)。因此,本研究假设,数学焦虑可能通过数学自我效能感和数学元认知间接影响数学成绩。
前人研究多关注大、中学生,而针对小学生的研究便于揭示数学焦虑、数学自我效能感等变量与数学成绩之间的关系是否在小学阶段就存在相应联系,尤其是小学高段学生是数学焦虑的高发年级,这对深入揭示数学成绩的影响因素有着突出意义。如果在小学阶段发现已存在数学焦虑影响数学成绩的作用机制,那么可以通过与中学生、成年人的作用机制进行对比,或采用追踪的方法,以发展的角度观察两者内在机制的变化趋势;此外,如果确认了这一作用机制,可以从更早的时间采取措施调控学生的数学焦虑,减少其对数学成绩的负面影响(Hill et al., 2016)。此外,相比城市学生,农村学生的数学焦虑现状更加严重,数学成绩更差,可能是由于农村教学硬件条件相对较差,学生对数学学习缺少兴趣和自信,不相信自己的数学能力(韩晓琳, 张康莉, 张晓明, 2016);农村学生的整体元认知水平也较低,学习策略使用更加单一、不灵活(张丽绵, 2009),从而可能导致各个变量在整个模式中所起的效果不同,并最终导致农村和城市小学生数学焦虑影响数学成绩的作用机制不同;或者数学焦虑影响数学成绩的作用机制可能未改变,但各变量所起的效果在程度上有所差异。所以,农村儿童的数学焦虑对数学成绩的负面影响在程度上可能更严峻,更需要相关研究进行揭示。
因此,本研究拟深入探究乡镇小学生数学焦虑、数学自我效能感、数学元认知与数学成绩之间的复杂作用机制,这对于提高乡镇小学生的数学学习成效和质量具有重要理论指导意义。本研究假设数学焦虑不仅可以直接影响数学成绩,而且可能通过数学自我效能感或数学元认知间接影响数学成绩,还可能通过数学自我效能感进而通过数学元认知间接影响数学成绩,即数学焦虑与数学成绩之间的关系可能存在链式多重中介效应。
2 方法 2.1 被试选取山东省某乡镇3所小学四、五、六年级的小学生共536人作为被试,剔除数据缺失在10%以上的被试和作答倾向明显的被试,最终有效被试508人,其中男生268人,女生240人,被试的平均年龄为11.45岁(SD=0.53岁)。
2.2 研究工具 2.2.1 儿童数学焦虑量表采用由Chiu & Henry编制(1990),耿柳娜、陈英和(2005)修订的《儿童数学焦虑量表》。该量表共22个项目,包含数学评估焦虑、数学问题解决焦虑、数学学习焦虑和数学教师焦虑4个维度,数学评估是指学生对自己学习成果的评估,因而数学学习评估焦虑指学生在面临与考试有关的情境时的焦虑反应;数学问题解决焦虑是指学生在可能引起厌倦的学习情境中,需要付出一定努力才能解决数学问题时的焦虑反应;数学学习焦虑是与数学学习过程或活动紧密相连的一种焦虑反应;数学教师焦虑指学生因为教师自身的一些特点或行为而产生的焦虑反应。量表共22个题目,使用4点量表评估焦虑程度。例如,“我清楚自己对已学过的数学知识的掌握程度”。采用4点计分法,从1(完全不焦虑)到4(极度焦虑),得分越高表示个体的焦虑水平越高。其中,KMO为0.91 (p>0.50),Bartlett检验值为2236.59,p < 0.001,本研究中的内部一致性系数为0.913。
2.2.2 小学生数学学习自我效能感量表采用刘电芝(2003)编制的《小学生数学学习效能感量表》,用于测量在数学情境下的自我效能感。该量表共20个项目,包含目标自信感、课程胜任感和课程应对感3个维度,例如,“我总是认为自己没有足够的能力学好数学”。采用5点计分,从1(完全不符合)到5(完全符合),其中有11个项目正向计分,9个项目反向计分,得分越高表示个体发展水平越高。其中,χ2/df值=4.40,GFI=0.83,NNFI=0.73,RMSEA=0.099,本研究中的内部一致性系数为0.902。
2.2.3 小学生数学元认知问卷采用由Panaoura & Philippou (2007)编制,郝嘉佳、齐琳和陈英和(2011)翻译修订的《小学生数学元认知问卷》,来考察小学生在课堂数学问题解决过程中对自身行为和经验的感知。该量表共30个项目,包含自我认知、自我调节、策略选择和动机4个维度,自我认知是指儿童对自己能力的信念和自我效能感;自我调节包含有关澄清问题目标、理解数学概念、应用已有知识生成解决问题的策略并监控问题解决的过程;策略选择是指用于解决问题和克服认知障碍的方法;动机是指儿童关于自己的努力和意愿以及家长和老师的期望影响数学学习的信念。采用5点计分,从1(从不)到5(总是),得分越高表示个体的元认知水平越高。其中,χ2/df值< 2,CFI和NNFI均在0.90以上,RMSEA < 0.08,本研究中的内部一致性系数为0.945。
2.2.4 数学成绩为保证数学成绩测量工具的同质性,所选被试都是来自同一地区,3所学校使用统一试卷。采用学生最近一次期末考试的数学成绩,将其原始成绩标准化,转化为标准分。
2.3 程序和数据处理以班级为单位进行团体施测,由研究者统一宣读指导语,被试独立完成问卷,总共时间大约20~25分钟,当场收回。采用EXCEL、SPSS19.0和AMOS17.0录入数据并对数据进行处理和分析。
3 结果由于采用自我报告方法,可能会存在共同方法偏差问题,采用Harman的单因素因子分析对共同方法偏差进行检验,结果表明未旋转时,特征值大于1的因子共17个,并且第一个因子解释了26%的方差变异,小于临界标准40%,表明本研究的共同方法偏差不显著。
3.1 初步分析为了探究不同年级的小学生在数学焦虑、数学自我效能感、数学元认知和数学成绩上是否有显著差异,分别运用单因素方差分析对四个变量进行统计分析,结果显示数学焦虑存在显著的年级差异,F(2, 505)=12.11,p < 0.001,四年级学生(M = 41.75,SD=11.91)的数学焦虑显著低于五年级(M = 44.58, SD=11.21)和六年级(M = 47.55, SD=10.76),五年级学生的数学焦虑显著低于六年级(p < 0.05)。数学元认知也存在显著的年级差异,F(2, 505)=10.04,p < 0.001,四年级学生(M = 14.10, SD=0.74)的数学元认知显著高于五年级(M = 13.17, SD=0.71)和六年级(M = 12.68, SD=0.63)。
为探讨对小学生的数学焦虑、数学自我效能感、数学元认知和数学成绩间的关系,对其进行皮尔逊相关分析。相关分析结果显示,数学焦虑和数学自我效能感、数学元认知、数学成绩之间均有中等程度的负相关,相关系数分别为-0.46、-0.54、-0.47;数学自我效能感和数学元认知、数学成绩有高度的正相关,相关系数分别为0.63、0.77;数学元认知和数学成绩之间也有高度正相关,相关系数为0.63。结果表明,在小学中、高年级中,数学焦虑、数学自我效能感、数学元认知与学生的数学成绩之间联系密切。
| 变量 | M±SD | 1 | 2 | 3 | 4 |
| 1数学焦虑 | 44.60±11.60 | 1 | |||
| 2数学自我效能感 | 3.37±0.66 | -0.46** | 1 | ||
| 3数学元认知 | 13.31±2.85 | -0.54** | 0.63** | 1 | |
| 4数学成绩 | 0±0.99 | -0.47** | 0.77** | 0.63** | 1 |
| 注: * p <0.05,** p<0.01,*** p <0.001。 | |||||
为了进一步考察数学焦虑与数学效能感、数学元认知和数学成绩的关系,检验数学效能感和数学元认知的中介作用,采用潜变量结构模型来构建四个变量之间的关系模型。在结构方程模型中,在控制年级后,以数学焦虑为预测变量、数学成绩为观测变量,数学效能感和数学元认知为中介变量建立为潜变量模型。
结果显示,该模型的拟合指数为:χ2 (49)=166.65,CFI、NFI、IFI和TLI都大于0.95,RMSEA < 0.08,说明模型拟合良好(吴明隆, 2010)。对模型(图 1)中的路径进行分析可知,数学焦虑对数学效能感和数学成绩都具有显著的负向预测作用(β= -0.488,p < 0.001;β = -0.138,p < 0.001);表明数学效能感对数学成绩具有显著的正向预测作用(β = 0.674,p < 0.001),说明数学效能感在数学焦虑和数学成绩的关系中起着部分中介作用。此外,数学焦虑对数学元认知具有显著的负向预测作用(β = -0.303,p < 0.001),数学效能感对数学元认知具有显著的正向预测作用(β = 0.528,p < 0.001),表明数学效能感在数学焦虑和数学元认知的关系中起着部分中介作用;数学元认知对数学成绩存在显著正向预测作用(β = 0.104,p < 0.001),所以数学元认知在数学焦虑和数学成绩间起着部分中介作用。本研究采用Bootstrap分析方法检验中介效应是否显著,置信区间设定为95%,如果路径系数95%的置信区间没有包括0,就说明中介效应显著。数学效能感在数学焦虑和数学成绩间的中介效应大小ab = -0.33,[-0.44, -0.09];数学效能感在数学焦虑和数学元认知间的中介效应大小ab = -0.26,[-0.39, -0.07];数学元认知在数学焦虑和数学成绩间的中介效应大小ab = -0.03,[-0.08, -0.01];数学元认知在数学效能感和数学成绩间的中介效应大小ab = 0.05,[0.03, 0.10];数学效能感和数学元认知在数学焦虑和数学成绩间的中介效应大小ab = -0.03,[-0.07, -0.01],置信区间都不包含0,因此,各路径系数显著,数学自我效能感和数学元认知在数学焦虑和数学成绩之间起到链式多重中介作用,数学焦虑不仅直接作用于小学生的数学成绩,而且通过数学自我效能感或数学元认知间接影响数学成绩,还可通过数学自我效能感进而通过数学元认知间接影响数学成绩。
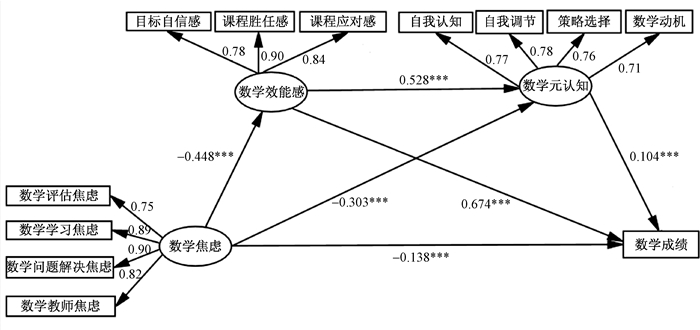
|
| 图 1 中、高年级小学生数学焦虑、数学效能感、数学效能感和数学成绩的关系模型图 |
本研究通过对508名乡镇中、高年级小学生进行调查,揭示了小学生的数学焦虑对数学成绩的影响,以及数学自我效能感和数学元认知在其中的中介作用。相关分析显示,小学生数学焦虑与数学成绩呈负相关,即数学焦虑越高的小学生,其数学成绩越差,这与以往的许多研究发现一致(Ashcraft & Krause, 2007; Devine et al., 2012; Jansen et al., 2013)。高数学焦虑个体的数学成绩差,使其产生不良的情绪体验,会更可能回避处理数学问题,逃避与数学相关的境况,进而使其数学成绩更差。
此外,本研究发现,数学焦虑可通过数学自我效能感间接影响数学成绩,即数学自我效能感在数学焦虑和数学成绩的关系中起部分中介作用。这个结果与孔令跃(2002)、张宁(2006)等人的研究结果一致, 也在一定程度上支持了干扰模型理论。高数学焦虑的学生,自信心低,不相信自己能解决数学相关的问题,会更加逃避与数学相关的境况,使得数学成绩更差(Carey et al., 2016)。这一研究结果也说明,数学焦虑程度较高的小学生,他们对自己、对与数学相关的任务问题更恐惧、更没有自信,他们的数学自我效能感更低,很难发挥自己的能力去解决数学问题,因此,这种不自信也会影响到其数学表现。在数学学习中恐惧遇到的问题,回避数学难题,无法取得较好的数学成绩。
同时,我们还发现,数学焦虑还可以通过数学元认知间接影响数学成绩。这一结果也在一定程度上支持了抑制型焦虑模型理论,即数学焦虑确实会通过过度占用加工资源,损害数学加工阶段的数学表现。一些实证研究已证明,个体的数学焦虑水平与工作记忆加工的广度和存储容量呈负相关(Ashcraft & Kirk, 2001; Eysenck & Calvo, 1992)。由于数学焦虑的个体,其担忧、恐惧会占用一部分数学认知加工资源,造成高工作记忆负载,影响了工作记忆的加工和存储,导致元认知资源不足,干扰元认知策略选择和使用的灵活性、流畅性,无法更好地解决数学问题,从而造成数学表现不良。这与以往的研究结果较为一致,被试的数学焦虑和被试的任务表现的相关性受到被试元认知水平高低的影响,但也有所差异。周双珠等(2014)的研究发现数学元认知在数学焦虑和数学成绩之间起完全中介作用,这与本研究中数学元认知起部分中介作用的结果不同。可能是由于农村小学生与城市小学生相比,数学元认知水平低,而数学焦虑高,所以数学焦虑影响数学成绩的作用机制虽然未改变,但各变量所起的效果在程度上有所差异。并且周双珠等人的研究结果虽然证明了数学元认知在数学焦虑和数学成绩之间起完全中介作用,但是中介效应只占33.9%,意味着仍有其他变量可能在其中起中介或调节作用,根据数学焦虑与表现的相关研究,城市中学生感知到的教师支持、父母支持和教学环境等可调节教学焦虑与表现间的关系。
更值得注意的是,本研究结果还显示数学自我效能感、数学元认知在数学焦虑与数学成绩的关系中发挥着链式多重中介作用。自我效能感理论认为,自我效能感对个体的行为具有重要的作用,它普遍影响着个体的动机和情感,决定人们的行为选择和行为结果(雷浩, 徐瑰瑰, 邵朝友, 桑金琰, 2015; 王伟, 雷雳, 王兴超, 2016; Wu et al., 2013)。其形成受情绪唤醒的影响,如强烈的厌恶、恐惧、焦虑等往往会降低数学自我效能感,使学生对自身的数学能力失去信心(李跃, 2014)。传统成就动机理论也指出数学自我效能感是成就动机中的一个积极成分,对任务选择和决定有重要的影响,高数学自我效能感会使学生解决数学问题时表现出较高的兴趣和注意,会提高使用数学元认知策略的灵活性和流畅性,并提高数学成绩(孔令跃, 2002)。因此,高数学焦虑会影响到小学生在数学方面的信心,而数学自我效能感则会进一步影响到他们的数学元认知和数学成绩,数学自我效能感越强的小学生,对于数学问题和自己的数学能力越有自信心和判断力,这种自信心和判断力能使小学生根据不同问题情境及时采用适宜的、多样化的策略,可以较为完美地组织、使用相应的认知资源,能更好地加工、处理数学问题,数学成绩也会越好;相反,高数学焦虑的学生会使数学自我效能感下降,降低了元认知策略使用的灵活性和流畅性,数学成绩也会变差。因此,在中、高年级阶段,小学生的数学焦虑可依次通过数学自我效能感、数学元认知间接影响数学成绩,即数学自我效能感和数学元认知在数学焦虑和数学成绩间起到链式多重中介作用,形成了“数学焦虑—数学自我效能感—数学元认知—数学成绩”这一作用路径。
本研究的上述发现拓展了数学焦虑的研究领域,探讨了小学生数学焦虑、数学自我效能感、数学元认知和数学成绩的关系,揭示了其作用机制,丰富了相关研究。此外,本研究结果也可为基础教育者和家长提供参考,有必要采取相应措施降低乡镇小学生的数学焦虑水平,注重培养、提高其数学自我效能感,有助于学生形成数学元认知能力,更好地运用认知资源,从而有效提升学生的数学成绩。不过,此前研究拟采用近两次的大型数学成绩,但由于乡镇小学的条件有限,数据保存并不完善,为了保证真实性和效度,只采用了有完整数据的最近一次数学成绩。Trujillo & Hadfield (1999)认为三方面会导致数学焦虑:环境、智力和人格。也有国内学者认为,数学焦虑的产生原因主要来自自身因素与环境因素两个方面,自身因素主要指学生对数学认知本身的体验及情感体验等;环境因素主要指学校与家庭,学校方面与老师、同伴群体和教学设计等因素有关,家庭与则与父母经济能力等有关(韩晓琳等, 2016)。因此,为了更好理解小学生的数学焦虑对数学成绩的作用机制,未来研究可以扩大研究对象的选取范围,增加城市样本,以进一步了解城市和乡镇学生在该方面的差异性和一致性,从而增强所得研究发现的概括性和可推广性。
5 结论数学焦虑不仅可通过数学自我效能感或数学元认知间接影响数学成绩,还可通过数学自我效能感进而通过数学元认知间接影响数学成绩。
| Ashcraft M. H., & Krause J. A. (2007). Working memory, math performance and math anxiety. Psychonomic Bulletin & Review, 14(2), 243-248. |
| Bernacki M. L., Nokes-Malach T. J., & Aleven V. (2014). Examining self-efficacy during learning:Variability and relations to behavior, performance, and learning. Metacognition & Learning, 10(1), 1-19. |
| Carey E., Hill F., Devine A., & Szücs D. (2016). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology, 6, 1987. DOI: 10.3389/fpsyg.2015.01987. |
| Chinn S. (2009). Mathematics anxiety in secondary students in England. Dyslexia, 15(1), 61-68. DOI: 10.1002/dys.v15:1. |
| Chiu L., & Henry L. L. (1990). Development and validation of the mathematics anxiety scale for children. Measurement & Evaluation in Counseling & Development, 23(3), 121-127. |
| Derakshan N., & Eysenck M. W. (2009). Anxiety, processing efficiency, and cognitive performance:New developments from attentional control theory. European Psychologist, 14(2), 168-176. DOI: 10.1027/1016-9040.14.2.168. |
| Devine A., Fawcett K., Szücs D., & Dowker A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions, 8(1), 33-41. DOI: 10.1186/1744-9081-8-33. |
| Eysenck M. W., & Calvo M. G. (1992). Anxiety and performance:The processing efficiency theory. Cognition & Emotion, 6(6), 409-434. |
| Guay F., Marsh H. W., & Boivin M. (2003). Academic self-concept and academic achievement:Developmental perspectives on their causal ordering. Journal of Educational Psychology, 95(1), 124-136. DOI: 10.1037/0022-0663.95.1.124. |
| Hill F., Mammarella I. C., Devine A., Caviola S., Passolunghi M. C., & Szűcs D. (2016). Maths anxiety in primary and secondary school students:Gender differences, developmental changes and anxiety specificity. Learning and Individual Differences, 48, 45-53. DOI: 10.1016/j.lindif.2016.02.006. |
| Hoffman B., & Spatariu B. (2008). The influence of self-efficacy and metacognitive prompting on math problem-solving efficiency. Contemporary Educational Psychology, 33(4), 875-893. DOI: 10.1016/j.cedpsych.2007.07.002. |
| Horn C., Bruning R., Schraw G., Curry G., & Katkanant C. (1993). Paths to Success in the College Classroom. Contemporary Educational Psychology, 18(4), 464-478. DOI: 10.1006/ceps.1993.1035. |
| Jacobse A. E., & Harskamp E. G. (2012). Towards efficient measurement of metacognition in mathematical problem solving. Metacognition and Learning, 7(2), 133-149. DOI: 10.1007/s11409-012-9088-x. |
| Jansen B., Louwerse J., Straatemeier M., Ven S., Klinkenberg S., & Maas H. (2013). The influence of experiencing success in math on math anxiety, perceived math competence, and math performance. Learning and Individual Differences, 24, 190-97. DOI: 10.1016/j.lindif.2012.12.014. |
| Krinzinger H., Kaufmann L., & Willmes K. (2009). Math anxiety and math ability in early primary school years. Journal of Psychoeducational Assessment, 27(3), 206-225. DOI: 10.1177/0734282908330583. |
| Lai Y., Zhu X., Chen Y., & Li Y. (2015). Effects of mathematics anxiety and mathematical metacognition on word problem solving in children with and without mathematical learning difficulties. Plos One, 10(6), e0130570. DOI: 10.1371/journal.pone.0130570. |
| Lee W., Lee M. J., & Bong M. (2014). Testing interest and self-efficacy as predictors of academic self-regulation and achievement. Contemporary Educational Psychology, 39(2), 86-99. DOI: 10.1016/j.cedpsych.2014.02.002. |
| Panaoura A., & Philippou G (2007). The developmental change of young pupils' metacognitive ability in mathematics in relation to their cognitive abilities. Cognitive Development, 22(2), 149-164. DOI: 10.1016/j.cogdev.2006.08.004. |
| Pennequin V., Sorel O., & Mainguy M. (2010). Metacognition, executive functions and aging:The effect of training in the use of metacognitive skills to solve mathematical word problems. Journal of Adult Development, 17(3), 168-176. DOI: 10.1007/s10804-010-9098-3. |
| Sabourin J. L., & Lester J. C. (2014). Affect and engagement in game-based learning environments. IEEE Transactions on Affective Computing, 5(1), 45-56. DOI: 10.1109/T-AFFC.2013.27. |
| Schraw G., & Dennison R. S. (1994). Assessing metacognitive awareness. Contemporary Educational Psychology, 19(4), 460-475. DOI: 10.1006/ceps.1994.1033. |
| Shams F., Mooghali A. R., Tabebordbar F., & Soleimanpour N. (2011). The mediating role of academic self-efficacy in the relationship between personality traits and mathematics performance. Procedia-Social and Behavioral Sciences, 29, 1689-1692. DOI: 10.1016/j.sbspro.2011.11.413. |
| Singh K., Granville M., & Dika S. (2002). Mathematics and science achievement:Effects of motivation, interest, and academic engagement. Journal of Educational Research, 95(6), 323-332. DOI: 10.1080/00220670209596607. |
| Stake J. E. (2010). The ability/performance dimension of self-esteem:Implications for women's achievement behavior. Psychology of Women Quarterly, 3(4), 365-377. |
| Trujillo K. M., & Hadfield O. D. (1999). Tracing the roots of mathematics anxiety through in-depth interviews with preservice elementary teachers. College Student Journal, 33(2), 219-222. |
| Verkijika S. F., & De Wet L. (2015). Using a brain-computer interface (BCI) in reducing math anxiety:Evidence from South Africa. Computers & Education, 81, 113-122. |
| Wang M. T., & Degol J. L. (2017). Gender gap in science, technology, engineering, and mathematics (stem):Current knowledge, implications for practice, policy, and future directions. Educational Psychology Review, 29(1), 119-140. DOI: 10.1007/s10648-015-9355-x. |
| Wu S. V., Huang H., Lee M., Wang T., Tung H., & Wu M. (2013). Self-efficacy, self-care behavior, anxiety, and depression in Taiwanese with type 2 diabetes:A cross-sectional survey. Nursing & Health Sciences, 15(2), 213-219. |
| Xu Z. H., & Jang E. E. (2017). The role of math self-efficacy in the structural model of extracurricular technology-related activities and junior elementary school students' mathematics ability. Computers in Human Behavior, 68(4), 547-555. |
| 崔吉芳, 李嫩晓, 陈英和. (2011). 数学焦虑影响儿童数学任务表现的作用机制探析. 心理发展与教育, 27(2), 118-125. |
| 耿柳娜, 陈英和. (2005). 数学焦虑对儿童加减法认知策略选择和执行的影响. 心理发展与教育, 21(4), 24-27. DOI: 10.3969/j.issn.1001-4918.2005.04.005. |
| 韩晓琳, 张康莉, 张晓明. (2016). 农村初中生数学焦虑及与数学成绩之间关系. 中国健康心理学杂志, 24(4), 596-599. |
| 郝嘉佳, 齐琳, 陈英和. (2011). 小学六年级数学困难儿童的元认知特点及其在应用题解决中的表现. 中国特殊教育, 11(2), 52-57. DOI: 10.3969/j.issn.1007-3728.2011.02.011. |
| 胡桂英, 许百华. (2003). 中学生学习自我效能感、学习策略与学业成就的关系. 浙江大学学报(理学版), 30(4), 477-487. DOI: 10.3321/j.issn:1008-9497.2003.04.028. |
| 孔令跃. (2002). 数学焦虑与数学成绩关系的研究(硕士学位论文). 首都师范大学, 北京. |
| 雷浩, 徐瑰瑰, 邵朝友, 桑金琰. (2015). 教师关怀行为与学生学业成绩的关系:学习效能感的中介作用. 心理发展与教育, 31(2), 188-197. |
| 李跃. (2014). 中学生数学焦虑、数学自我效能感、数学学习动机对数学成绩的影响(硕士学位论文). 东北师范大学, 长春. |
| 刘电芝. (2003). 小学儿童数学学习策略的发展与加工机制研究(博士学位论文). 西南师范大学, 重庆. |
| 刘星辰, 原露, 陈启山. (2016). 数学焦虑与数学自我效能感对数学素养的影响:来自PISA的结果. 考试研究, 14(2), 89-93. |
| 申继亮, 陈英和. (2014). 中国教育心理测评手册. 北京: 高等教育出版社. |
| 司继伟, 徐艳丽, 封洪敏, 许晓华, 周超. (2014). 不同数学焦虑成人的算术策略运用差异:ERP研究. 心理学报, 46(12), 1835-1849. |
| 孙洲. (2010). 小学高段学生的数学焦虑及其教育对策研究(硕士学位论文). 温州大学, 温州. |
| 王伟, 雷雳, 王兴超. (2016). 大学生主动性人格对学业成绩的影响:学业自我效能感和学习适应的中介作用. 心理发展与教育, 32(5), 579-586. |
| 吴明隆. (2010). 问卷统计分析实务:SPSS操作与应用. 重庆: 重庆大学出版社. |
| 张丽绵. (2009). 农村普通高中学生数学元认知水平的调查和培养研究(硕士学位论文). 河北师范大学, 石家庄. |
| 张宁. (2006). 高中数学焦虑、数学自我效能感与数学成绩的关系(硕士学位论文). 河北师范大学, 石家庄. |
| 周双珠, 韩瑽瑽, 陈英和. (2014). 数学焦虑影响数学学业成就的作用机制. 数学教育学报, 23(5), 1835-1849. |
| 庄鸿娟, 刘儒德, 刘颖. (2016). 中学生社会支持对数学学习坚持性的影响:数学自我效能感的中介作用. 心理发展与教育, 32(3), 317-323. |
 2018, Vol. 34
2018, Vol. 34


