国家教育部主管、北京师范大学主办。
文章信息
- 高瑞彦, 牛美心, 杨涛, 周新林. 2018.
- GAO Ruiyan, NIU Meixin, YANG Tao, ZHOU Xinlin. 2018.
- 4~8年级学生分数数量表征的准确性及形式
- The Accuracy and Form of Fraction Magnitude Representation for 4 to 8 Graders
- 心理发展与教育, 34(4): 443-452
- Psychological Development and Education, 34(4): 443-452.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2018.04.08
2. 北京市大兴区地方税务局, 北京 102600;
3. 北京师范大学认知神经科学与学习国家重点实验室, 北京 100875
2. Beijing Daxing Local Taxation Bureau, Beijing 102600;
3. National Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Beijing 100875
分数是人类处理现实世界中两个量之间关系的有力数学工具,对数学学习有重要意义。近些年来关于分数学习的研究更多地关注分数数量表征,它是一种重要的数学认知能力,不仅影响分数学习本身(如理解分数概念与掌握分数运算法则),还会影响到代数学习与数学学业成就(Bailey, Hoard, Nugent, & Geary, 2012; Booth & Newton, 2012; Siegler, Thompson, & Schneider, 2011; Siegler et al., 2012; Wang & Siegler, 2013)。
已有研究为分数数量可以在心理数字线(mental number line)上进行表征提供了依据。Schneider和Siegler(2010)在分数大小比较实验中选取复杂的异分子异分母分数作为刺激材料,结果发现,与分子或分母间的距离相比,分数数量实际值(real value)间的距离更好地解释了被试的反应时和准确率。为避免数字符号对分数数量表征的干扰,辛自强和李丹(2013)在分数大小比较任务中用非符号分数代替符号分数,进一步证明个体能够对分数实际值(real value)进行表征。脑神经核磁的研究发现,被试在对分数大小进行表征时,具有对分数值间的距离进行表征功能的大脑顶内沟异常活跃(Ischebeck, Schocke, & Delazer, 2009; Jacob & Nieder, 2009)。这些结果均证明个体对分数数量的表征建立在连续量的基础上,即个体可以将分数从小到大按照从左到右的顺序映射到心理数字线上(Hevia & Spelke, 2009)。
有关分数数量表征的准确性,已有研究表明分数数量表征准确性随着个体年级或年龄的增长而提高,这在中西方的儿童被试中都有体现(Siegler et al., 2011;孙玉,司继伟,黄碧娟,2016;辛自强,李丹,2013)。Siegler等(2011)对分数数量表征发展的研究表明,八年级学生分数估计准确性高于六年级学生。辛自强和李丹(2013)对小学三到六年级学生在非符号材料上的分数表征研究发现,学生的表征准确性随着年级上升而显著提高。这些关注分数数量表征准确性的研究在年级发展趋势上主要体现在小学生阶段或者初中生阶段。与西方儿童相比,中国儿童可能具有更高的分数数量表征准确性。无论六年级还是八年级,中国学生的分数数量表征准确性高于美国等其它国家的学生(Bailey et al., 2015;Torbeyns, Schneider, Xin, & Siegler, 2015)。
分数包含了单位分数(即分子为1的分数)和非单位分数(即分子不为1的分数)两个基本类型,由于表征思维过程的不同,它们在数量表征准确性上也存在差异(Bonato, Fabbri, Umiltà, & Zorzi, 2007;Booth & Newton,2012;Booth, Newton,& Twissgarrity,2014;郭红力, 2010)。Booth和Newton(2012)的研究表明个体对两类分数进行表征时采用的思维过程有差异,对单位分数数量进行表征,个体需要找出分数所代表单位的大小;对非单位分数数量进行表征,个体需要进行比率的转化。Bonato等(2007)通过四个实验研究了71名大学生在单位分数上的表征形式,结果表明被试对分数进行表征时主要根据分数中某个具体的成分(如分子或分母)。同Bonato等(2007)对分数成分表征的解释类似,郭红力(2010)认为对单位分数的估计只需要考虑分母,而在估计非单位分数时要同时考虑分子和分母,因此对单位分数估计的准确性高于非单位分数,但只在位置数字(PN)任务上发现了这一差异;这项研究没有发现两类分数表征差异上的年级变化,也没有对年级增长趋势进行研究。基于先前研究可知,相对于单位分数,非单位分数表征可能涉及到更为复杂的思维过程导致个体对单位分数表征准确性高于非单位分数,但对两类分数表征准确性上的差异随着年级增长而呈现出的变化趋势尚不清楚。
对于分数数量表征的形式,目前有单一形式和混合形式两种观点。分数表征形式为单一的线性表征还是多种形式的混合表征尚处在争论之中,且在不同的年龄发展阶段也可能存在表征形式上的不同(Bonato et al., 2007; Jacob & Nieder, 2009; Liu, Xin, Lin, & Thompson, 2013; Siegler et al., 2011; 陈英和,2015; 郭红力, 2010; 张丽, 卢彩芳, 杨新荣, 2014; 张丽, 辛自强, 王琦, 李红, 2012)。Siegler根据Dehaene(1997)的理论,认为个体对分数数量表征,尤其是异分子异分母分数,只存在线性表征形式,不存在对数表征形式。Siegler等(2011)利用数字线估计任务证明了这一假设。他们以六年级和八年级学生为被试,要求被试在0~1和0~5的数字线范围上估计10个异分子异分母分数的位置。通过曲线估计发现在0~1数字线上,六八年级学生的表现都与线性函数拟合好,其表征的线性函数的斜率与1更接近。在0~5数字线上,八年级学生的表现与线性函数拟合好,而六年级学生的表现没有函数与之拟合。说明个体对异分子异分母分数的数量表征只存在线性表征形式,且这种线性形式只有儿童的数量表征能力发展到一定程度才会出现。无论对中国儿童还是西方儿童,目前多数研究表明分数表征只存在线性表征,或非线性表征向线性表征的发展,并不支持两种表征形式共存的理论(Siegler et al., 2011; 陈英和,2015;张丽等,2014)。并且中西方儿童线性表征形式出现的年龄是有差异的。张丽等(2014)研究表明,与三四年级儿童相比,五六年级儿童已经形成了分数数量的线性表征形式(0~1数字线);但Siegler等(2011)的研究中线性表征形式出现的年级可能更晚,不同的数字线范围可能会影响线性表征形式出现的年龄(陈英和,2015)。
郭红力(2010)的观点与Siegler的观点不同,他认为重叠波理论(Booth & Siegler, 2006; Siegler, 1996; Siegler & Opfer, 2003)对分数数量表征同样适用,即个体对分数数量的表征也能够使用多种表征形式。具体表征形式与数字情境有关,在熟悉的数字情境中,个体采用线性表征形式;在不熟悉的数字情境中,个体采用对数表征形式。在实验中他要求六年级儿童和大学生在0~1数字线上对异分子异分母分数和分子为1的分数进行估计,在1/100~1/10数字线上对分子为1的分数进行估计,结果发现被试在0~1(熟悉的数字环境)数字线上对两类分数都采用线性表征的形式,在1/100~1/10(不熟悉的数字环境)数字线上采用对数表征的形式。他认为这个实验结果说明重叠波理论在分数数量表征中同样适用,数字线范围会影响到个体对分数数量的表征形式。但是,该实验材料无论分数范围还是具体分数都相对比较特殊。
分数数量表征的研究方法通常采用数字线任务,刺激材料可以选择真分数、假分数、带分数等多类分数,数字线环境可以为常规的0~1、0~3、0~5等环境,即数字线左右端点均为整数(Siegler et al., 2011);也可以为1/1~1/1440等环境,左右端点为分数(Opfer & Devries, 2008; Opfer, Thompson, & Devries, 2007)。
通过文献回顾发现,分数数量表征还存在一些值得继续研究的内容。一是已有研究集中于小学阶段或者初中阶段,缺少对从小学阶段(儿童时期)到初中阶段(青少年时期)的变化趋势研究。年级或者年龄跨度较小,不容易观察到发展趋势,但从小学阶段到初中阶段(六和八年级),学生在部分数学认知发展的任务中表现出差异(Siegler et al., 2011)。另外,分数表征尤其是符号表征,与学生学习分数的经验相关,考虑到我国三年级的分数学习内容为“分数的初步认识”(且分母为十以内),选取四年级为起始被试年级相对合理。此外,对中国文化背景下的儿童进行研究,可以与已有研究中西方儿童在分数数量表征上的跨文化差异进行更加深入的分析比较。
二是个体对单位分数和非单位分数数量表征的情况不明朗,尤其是随着年级的变化两类分数表征准确性的差异是否发生变化,以及如何变化,尚没有充分研究证据。根据已有研究,可以提出“4~8年级学生对单位分数表征的准确性高于对非单位分数表征的准确性”的假设(Bonato et al., 2007;Booth & Newton,2012;郭红力, 2010),但两类分数表征准确性差异的变化趋势,缺乏直接的研究证据。在数字认知发展的部分任务中,如数字空间表征、数量比较大小、估算等,随着年级或年龄的增加,被试完成任务的准确性越高,部分任务中八年级和大学生(或成人)的表现已经没有显著差异(Berch, Foley, Hill, & Ryan, 1999;Girelli, Lucangeli, & Butterworth, 2000;Lemaire & Lecacheur, 2002;Siegler et al., 2011;Van Galen & Reitsma, 2008)。据此可提出两类分数数量表征准确性的差异随年级增高逐渐减少的假设。另外,对两类分数表征准确性的差异研究多是西方文化背景下的儿童,较少有中国文化背景下儿童的表现。
三是个体对分数数量表征的形式没有明确结论。重叠波理论(多表征假说)由Siegler(1996)提出后,主要是在整数数量估计等任务中得以证实(Siegler & Opfer,2003),反映了儿童对大、小数量认识的熟悉程度不同,但随着年龄增加,对数量范围和熟悉度增加,只出现了线性表征。儿童对分数,尤其是符号表征的分数认识,是在对整数数量认识的基础上得以发展,对分数的表征是以分数的实际值进行表征(Schneider & Siegler, 2010;辛自强,李丹,2013),遇到不同分数的几率与分数大小无关。且基于已有研究中,多数结果表明分数数量只存在线性表征,或非线性表征向线性表征的发展,并不支持两种表征形式共存的理论(Siegler et al., 2011; 张丽等,2014),研究倾向于假设分数数量表征的形式为线性表征。此外,通过对中国儿童分数表征形式的研究,也可以为不同文化中线性表征形式的出现年龄提供更多研究证据。
在不同文化背景下,分数数量表征的准确性和表征形式可能存在差异。已有研究揭示了中国儿童在数学学业表现以及整数的数量加工、数字估计等任务上都有更好的表现(Mullis et al., 2008; Mullis, Martin, Foy, & Arora, 2012;Siegler & Mu, 2008; Stevenson, Chen, & Uttal, 1990; Zhou, Peverly, & Lin, 2005;周广东, 莫雷, 温红博, 2009),而整数数量表征与分数数量表征存在正相关(Fazio, Bailey, Thompson, & Siegler, 2014;张丽等,2014)。通过对分数数量表征的相关研究进行分析,中国儿童与西方儿童可能有相似的发展路径,但可能在准确性上高于西方儿童、线性表征出现时间上早于西方儿童。
综上分析,本研究选取4~8年级学生,探索在0~3数字线环境中分数数量表征的准确性及表征形式,具体问题是:4~8年级学生分数数量表征的准确性上,对单位分数和非单位分数表征准确性的差异是什么,该差异随着年级的变化如何变化?4~8年级学生对分数数量表征的形式是什么?基于已有研究,提出以下研究假设:
(1) 4~8年级学生对单位分数表征的准确性高于对非单位分数表征的准确性,两类分数表征准确性的差异随年级增加逐渐减小;
(2) 4~8年级学生对分数数量表征为线性表征形式;
(3) 中国儿童与西方儿童有相似的发展路径,但在表征准确性上高于西方儿童、线性表征出现时间上早于西方儿童。
2 方法 2.1 被试从北京市某郊区县选取两所小学的4~6年级学生和两所初中的7、8年级学生,被试分布情况见表 1。
| 年级 | 男生 | 女生 | 总计 |
| 四年级 | 81 | 72 | 153 |
| 五年级 | 62 | 74 | 136 |
| 六年级 | 105 | 62 | 167 |
| 七年级 | 105 | 116 | 222 |
| 八年级 | 82 | 82 | 165 |
| 总计 | 435 | 406 | 843 |
本研究采用分数数字线估计任务。
任务采用5(年级:4~8年级)×2(分数类型:单位分数;非单位分数)的实验设计。其中年级为组间变量,分数类型为组内变量,因变量为被试在数字线上所确定的位置。刺激材料为20个分数1/10, 1/12, 1/14, 1/15, 1/17, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 10/12, 10/13, 10/18, 10/19, 11/12, 11/14, 11/16,其中单位分数13个,非单位分数7个。
2.3 实验程序 2.3.1 培训主试在施测前,主试需要参加培训,熟悉整个测试过程,包括指导语内容、实验程序和实验过程中的注意事项等。达到施测要求后,主试方能参加测试工作。
2.3.2 正式实验本次测试采用集体施测方式,借用“多维心理网络平台”中的数字线估计任务。正式施测前,被试先完成5个练习,以便了解整个实验过程和操作方法。
正式施测开始后,屏幕上出现一条0~3的白色线段,左边标有0,右边标有3,线段左上方出现一个分数(比如1/2)。被试估计出1/2在0~3数字线的位置后,用鼠标点击该位置,在该位置会出现一条白色竖线表示被试估计的1/2的位置,被试确认之后点击左下方的“提交”按钮,计算机程序能够记录被试的应答反应。每做完一题,被试点击屏幕下方“下一题”按钮,当20个分数的位置都估计完后,屏幕上会自动出现“测验完成”的字样,表示测验结束。
2.4 数据分析采用SPSS20.0软件对收集的数据进行分析。
表征准确性使用Siegler研究中经典的准确性指标——“绝对误差百分比(percent absolute error,PAE)”。计算方法为PAE=∣估计值-实际值∣÷被估计的数值范围。比如要求被试估计1/2在0~3数字线上的位置,而某被试标出的位置实际是1/3所在的位置,那么该被试的绝对误差百分比便是∣1/3-1/2∣÷3。由此可见,PAE是一个负向指标,PAE值越大,被试估计的误差越大。
表征形式使用曲线估计的方法进行分析。首先计算学生对每个分数估计的中值(以降低极端值的影响),然后以估计值为自变量,以分数实际值为因变量,进行曲线估计,分别采用线性函数和对数函数的曲线拟合。如果与线性函数拟合得好,则说明学生表现为线性表征形式;如果与对数函数拟合得好,则说明学生表现为对数表征形式。
3 研究结果 3.1 分数数量表征的准确性以分数类型(单位分数;非单位分数)为组内变量,年级(4~8年级)为组间变量进行2×5的重复测量方差分析,具体结果如下:
(1) 分数类型主效应显著:F(1, 797)=789.81,p<0.001,η2=0.50。单位分数和非单位分数的PAE分别为18.97%和22.56%,被试对单位分数数量估计的准确性高于对非单位分数数量的估计。
(2) 年级主效应显著,F(4, 797)=26.41,p<0.001,η2=0.12。
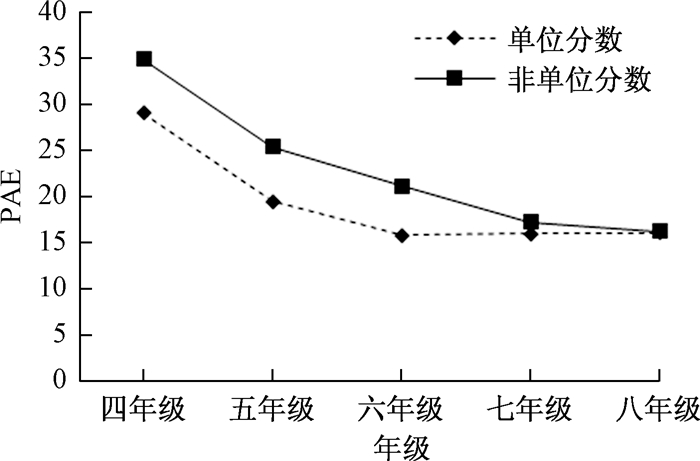
(3) 分数类型与年级的交互作用也非常显著,F(4, 797)=86.76,p<0.001,η2=0.30。交互作用见图 1。可以看出学生在四到六年级阶段对于非单位分数数量表征的准确性显著低于单位分数的数量表征,在两种类型分数数量表征的准确性都随着年级增长而迅速提高时,两类分数表征之间的差异也逐渐减小;而到了七八年级阶段,两类分数表征的准确性都趋于平缓,且两者之间的差异逐渐消失。
|
| 图 1 各年级两类分数数量表征 |
再进一步分析简单效应,分别对两类分数数量表征的PAE进行分析,结果见表 2。
| 四年级 | 五年级 | 六年级 | 七年级 | 八年级 | F | p | 事后比较 | |
| 单位分数PAE | 29.11 | 19.46 | 15.78 | 15.91 | 16.01 | 19.96 | 0.000 | 4>5>6 |
| 非单位分数PAE | 34.92 | 25.36 | 21.16 | 17.21 | 16.17 | 32.21 | 0.000 | 4>5>6>7 |
从表 2可知,四至八年级被试的单位分数PAE存在显著的年级差异,F(4, 797) =19.96, p<0.001。进行事后比较,发现只有四、五、六年级被试的差异显著,随着年级增长,PAE逐渐降低;六、七、八年级被试的PAE没有显著差异。这说明六年级前被试对单位分数表征的准确性有比较明显的提升,六年级被试对单位分数表征的准确性相对稳定,六年级至八年级被试对单位分数表征的准确性保持在一个相对比较高的水平上。
四至八年级被试的非单位分数PAE存在显著的年级差异,F(4, 797) =32.21, p<0.001。进行事后比较,发现只有四、五、六、七年级被试的PAE差异显著,随着年级增长,PAE逐渐降低;七八年级被试的PAE没有显著差异。这说明,七年级前被试对非单位分数表征的准确性有比较明显的提升,七年级被试对非单位分数表征的准确性相对稳定,七年级至八年级被试对非单位分数表征的准确性保持在一个相对比较高的水平上。
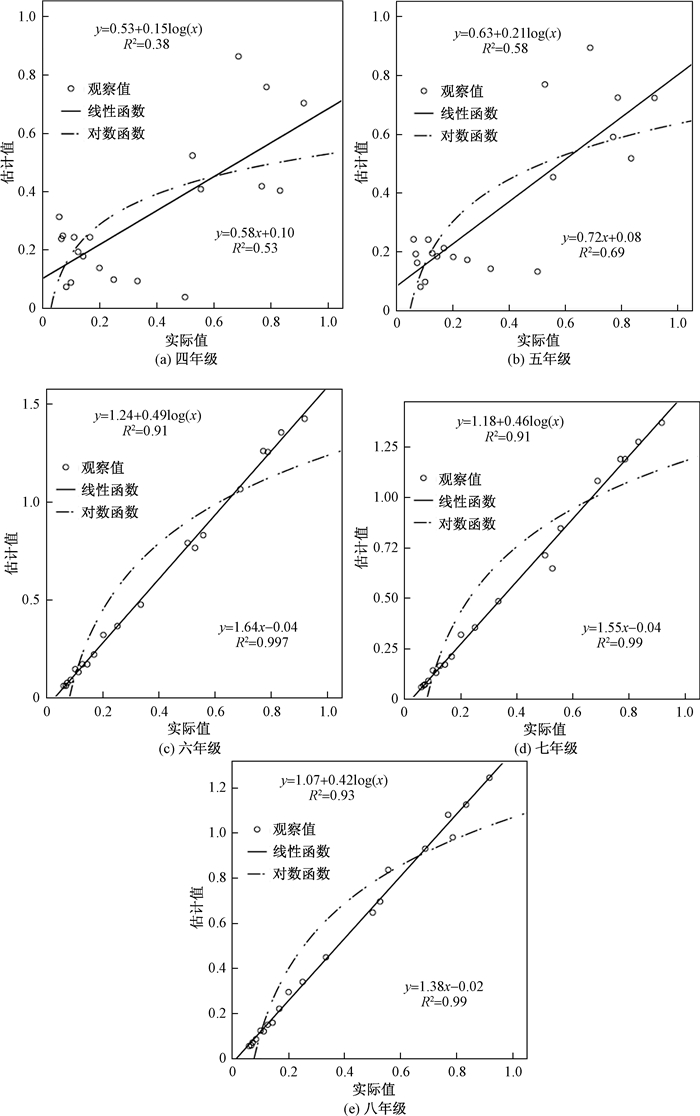
3.2 分数数量表征形式对每个被试对应的20个分数估计值进行曲线估计。由于研究采用的是数字位置(NP)估计方法,基于前人相关研究(Liu, 2017;Siegler et al., 2011; Stapel, Hunnius, Bekkering, & Lindemann, 2015;卢淳,郭红力,司继伟,孙燕,2014;张帆,赖颖慧,陈英和,2015),分别采用线性函数和对数函数的曲线拟合,拟合结果见图 2。总体上,线性函数与4~8年级被试的分数数量表征的拟合度比对数函数较高。
|
| 图 2 分数数量表征形式 |
为了更加确定地判断被试表征时采用的形式,将线性函数和对数函数差异的显著性进行检验。检验过程是,先求得两模型产生的预测值,再将预测值的绝对误差进行配对t检验,结果显示:四年级被试的线性模型和对数模型的拟合程度不存在显著差异[t(19)=-2.48, p=.086, ns];五年级被试的线性模型和对数模型的拟合程度不存在显著差异[t(19)=-1.78, p=.091, ns];六年级被试[t(19)=-7.81, p<0.001],七年级被试[t(19)=-5.51,p<0.001]和八年级被试[t(19)=-3.50,p<0.001]的线性模型和对数模型拟合程度差异显著。说明被试在四年级和五年级没有出现较为明显的线性或对数表征形式,在六年级之后出现较为明显的线性拟合形式。
4 讨论 4.1 分数数量表征准确性的年级或年龄发展趋势分数数量表征的PAE随着年级增长而降低,说明个体对分数数量的表征随年龄增长越来越趋向于准确。此结果与Siegler等(2011)、辛自强和李丹(2013)的研究结果相同;但是与Opfer et al.(2007)、Opfer和Devries(2008)的研究结果不一致,他们发现成人分数数量表征的准确性反而低于儿童。之所以出现这样的不同,可能是因为实验任务有差异。Opfer等人的实验要求被试估计分子为1的分数在1/1~1/1440的数字线上的位置,这种两端为分数的数字线很容易迷惑被试,被试非常容易以分母为参考对分数进行估计,从而将整数数量表征带入到分数数量表征中。这种估计方法,显然对于整数数量表征准确的成人是不利的。因为对分子为1的分数,分母的值与分数值是呈幂函数的关系,分母越大,分数值越小,且分数值越小变小的速度越慢,而整数变化速度是均匀的。因此,对整数采用线性表征的个体会扩大分母大而实际值小的分数之间的距离。也就是说对整数表征越准确的被试,在Opfer等人的任务中对分子为1的分数的表征可能越不准确。这种实验任务的差异可能是导致本研究与Opfer等的研究结果有差异的原因。
最近多项研究也表明分数数量表征的准确性随着年龄或年级增长而提高(陈英和,2015;卢淳等,2014;张帆等,2015)。卢淳等(2014)采用了0~1和1/100~1/10两种数字线条件下数字位置和位置数字估计任务考察了儿童和成人的分数表征,发现儿童在两种数字线条件下准确性均低于成人。
另外,本研究结果也揭示在分数数量表征的跨学段发展过程中,四五六年级学生分数表征的准确性发展相对比较明显,而六七八年级相对趋缓,但主要在单位分数和非单位分数的表征准确性及其发展上表现出差异。
4.2 两类分数数量表征准确性的差异被试对单位分数表征的准确性高于非单位分数,可能是因为将两类分数表征在数字线上需要不同的思维过程。将单位分数表征在数字线上只需要找出分数所代表的单位大小,而将非单位分数表征在数字线上需要进行比率转化,与早期代数知识有关(Booth & Newton, 2012;Booth et al., 2014)。比如,将1/3表征在数字线上,被试只需找到三等分点的位置;而将4/29表征在数字线上,被试需要判断4/29表示的数量接近于0.15,这涉及更多的思维过程。这种思维难度的差异导致学生对两类分数表征准确性的不同。
从两类分数表征与年级的交互作用结果发现,低年级学生对单位分数表征的准确性显著高于非单位分数,随着年级增长,两类分数表征准确性之间的差异逐渐消失。虽然个体对两类分数的表征随年级增加准确性逐渐提高,但不同分数类型上的年级发展趋势不同,对单位分数的认识在六年级比较稳定,而对非单位分数的认识在七年级才比较稳定。这可能源于两类分数表征上不同的思维过程,使得个体对于非单位分数成熟且稳定的认识晚于对单位分数的认识(Booth & Newton, 2012;Booth et al., 2014)。
另外,随着年级增加,被试在数字空间表征、数量大小比较、估算等任务上的准确性提高,部分任务中八年级和大学生表现已没有显著差异,小学生到初中生在单位分数和非单位分数上表征准确性差异逐渐减小,也体现了准确性发展趋势到了某个年龄阶段可能会趋于稳定状态(Berch et al., 1999;Girelli et al., 2000;Lemaire & Lecacheur, 2002;Siegler et al., 2011;Van Galen & Reitsma, 2008)。最后,学生在进入初中阶段以后代数学习经验的增加也可能有益于提高非单位分数表征的准确性,使其逐渐接近对单位分数表征的准确性(Booth et al., 2014)。
4.3 分数数量表征的形式四五年级被试估计中值与分数实际值的线性函数与对数函数的拟合度均不高,且不存在显著差异;六到八年级被试估计中值与20个分数线性函数的拟合度高于对数函数,表明这三个年级的被试分数数量表征呈线性形式,且随年级增长,线性函数的斜率越接近于1。学生在0~3数字线范围内,分数数量表征为线性表征形式,且线性形式是随被试对数量的准确认知逐步发展起来的,这与Siegler et al.(2011)的研究结果一致。与本研究结果类似,张丽等(2014)的研究表明,五六年级儿童已经形成了分数数量的线性表征形式,三四年级儿童没有表现出明显的对数或线性表征。
个体没有表现出对数表征形式,可能是因为分数没有产生对数表征形式的条件。虽然Siegler(1996)提出了重叠波理论(多表征假说),但主要在整数数量估计等任务中得以证实(Siegler & Opfer,2003)。儿童在对整数数量认识的基础上,进一步发展对分数,尤其是符号表征的分数认识。Dehaene和Mehler(1992)认为对整数的对数表征形式反映了人们遇到不同大小数字的几率。对整数而言,人们遇到小数字的几率大于大数字,对小数字比对大数字熟悉,因此小数字间的距离在心理表征上会更大,而大数字相反。比如,与82和84相比,我们经常遇到2和4,人们会认为2与4之间的距离大于82与84间的距离(Dehaene, 1997),这样就会产生数量表征的对数形式。然而,我们遇到不同分数的几率与分数大小无关。比如我们遇到1/2、1/4等分数的几率要大于小分数1/29和大分数28/29。如果遇到整数的几率可以解释整数的对数表征形式,而遇到分数的几率与分数大小无关,那么个体对分数是不大可能表现出对数表征形式的。这也印证了Schneider和Siegler(2010),Ischebeck et al.(2009),Jacob和Nieder (2009)以及辛自强和李丹(2013)关于个体对分数数量表征的观点:个体能够把分数的实数值表征在心理数字线上,即个体可以将分数看作整体进行表征。
综上,虽然线性表征形成的时间及形成机制尚无定论,但可以认为分数的线性表征形式是一个随着年级或年龄发展逐渐形成的过程;在符号数量表征发展中,分数数量表征形式是一个由非线性到线性形式转变的过程(陈英和,2015)。
4.4 中西方儿童分数数量表征准确性与形式的跨文化分析本研究结果基于中国儿童被试得到,不同文化背景下可能存在一定差异。
首先,在分数数量表征准确性的年级变化趋势上,中西方儿童具有相同表现。已有中国儿童和西方儿童的研究分别得到了相同的结论(Siegler et al., 2011;卢淳等,2014;辛自强,李丹,2013;张帆等,2015),即准确性随着年级或年龄增长都有提高的趋势。这在跨文化研究中也得到直接验证(Bailey et al., 2015)。在0~1和0~5数字线上,对中国、比利时和美国学生,八年级分数数量表征的准确性都高于六年级(Torbeyns et al., 2015)。
但跨文化研究也发现分数数量表征的准确性上有国家间差异,对六八年级学生来说,都表现为中国最好,比利时次之,美国最低(在0~1数字线上,中国与比利时差异不显著)。这可能与中国学生具有更好的数学学业表现以及整数数量加工表现等有关,也可能与各国不同的课程内容、教师教学等有关(Mullis et al., 2008, 2012;Siegler & Mu, 2008; Stevenson et al., 1990; Zhou et al., 2005;周广东等, 2009)。
其次,两类分数表征准确性及其差异变化上,中西方儿童也可能存在相似表现。中国儿童单位分数表征的准确性高于非单位分数,与已有西方研究结果一致(Bonato et al., 2007;Booth & Newton, 2012)。另外,两类分数表征准确性的差异变化趋势上虽然还没有直接的跨文化研究,但在整数数量表征、数量比较等相关任务中(Berch et al., 1999;Girelli et al., 2000;Lemaire & Lecacheur, 2002;Siegler et al., 2011;Van Galen & Reitsma, 2008),被试随着年级增加准确性提高,在部分任务中八年级和大学生表现已没有显著差异。整数数量表征与分数数量表征存在一定正相关(Fazio et al., 2014;张丽等, 2014),因此,西方文化背景下儿童分数数量表征的发展到了某个年龄段也可能趋于稳定,即两类分数表征上可能与中国儿童存在相似的发展路径。
但在趋于稳定的具体年级上可能不同。儿童对分数的认识和理解比整数更复杂,中国儿童对两类分数表征准确性在七年级趋于稳定,西方儿童可能晚于中国儿童。
第三,在表征形式上,中西方儿童都表现出线性形式。本研究结果支持了Siegler等(2011)对六八年级美国儿童得到的结论,即分数表征只存在线性形式。张丽等(2014)的研究,也支持分数表征的单一形式。可见,虽没有跨文化的直接研究,不同文化下的独立研究都印证了分数表征的单一形式假设。
但在线性表征出现的年级上,中西方儿童存在差异。本研究采用0~3数字线,六、七、八年级出现线性形式;Siegler等(2011)的研究,0~1数字线上美国学生六八年级为线性表征,0~5数字线上只有八年级的表现与线性函数拟合好;张丽等(2014)的研究,采用0~1数字线,五、六年级形成了分数数量的线性表征形式。对中西方儿童来说,不同数字线范围可能会影响线性表征形式出现的年龄,即数字线范围越小,出现的年龄也越早(陈英和,2015);另外,因为儿童的数量表征能力发展到一定程度才出现线性形式(Siegler et al., 2011),中国儿童在分数数量表征准确性、分数比较等任务上的表现都好于美国儿童(Torbeyns et al., 2015;Bailey et al., 2015),美国儿童出现线性形式的年级可能晚于中国儿童。
综上,中国儿童与西方儿童有相似的发展路径,但可能在准确性上高于西方儿童、线性表征出现时间上早于西方儿童。
4.5 研究不足与展望本研究任务情境只选择了0~3的数字线环境,没有类似其他研究者采用两种数字线环境进行对比(Siegler et al., 2011)。因本研究重点是探索单位分数与非单位分数表征情况,意不在比较不同数字环境中的表现,所以只选择了0~3数字线环境。以后研究可以增加不同数字线环境,对比学生在不同环境中两类分数表征的情况。
考虑到非单位分数表征思维过程的复杂性以及测试时间限制,本研究刺激材料采用的单位分数多于非单位分数,虽然被试量较为充足,但今后研究中还可以考虑对两类分数设置同样或相近数量的刺激材料,也可以考虑熟悉非单位分数与不熟悉非单位分数的情形(Booth & Newton, 2012;Booth et al., 2014;郭红力,2010)。再者,本研究只选取了数字线估计的数字位置任务,并没有考察位置数字任务,两种任务下可能存在不同的分数数量表征形式也是需要考虑的方向(卢淳等,2014)。另外,采用相同数字线范围,对不同文化背景的儿童进行直接的跨文化比较研究,也是今后值得考虑的方向。
5 结论随着年级升高,被试分数数量表征的准确性也随之提高;被试对两类分数(单位分数和非单位分数)表征的准确性存在显著差异,对单位分数表征的准确性显著高于非单位分数,这种差异在低年级显著,随着年级增长,差异逐渐消失;四到八年级学生在0~3数字线上,分数数量表征表现为线性形式而非对数形式,且这种线性形式是在六年级开始出现并随年龄增长逐渐发展起来的。中西方儿童在分数数量表征的准确性和形式上有相似的发展路径,但是在表征准确性上中国儿童更高、线性形式出现时间上中国儿童可能更早。
| Bailey D. H., Hoard M. K., Nugent L., & Geary D. C. (2012). Competence with fractions predicts gains in mathematics achievement. Journal of Experimental Child Psychology, 113(3), 447-455. DOI: 10.1016/j.jecp.2012.06.004. |
| Bailey D. H., Zhou X., Zhang Y., Cui J., Fuchs L. S., & Jordan N. C. (2015). Development of fraction concepts and procedures in u. s. and chinese children. Journal of Experimental Child Psychology, 129, 68-83. DOI: 10.1016/j.jecp.2014.08.006. |
| Berch , Daniel B., Foley , Elizabeth J., Hi ll, Rebecca J., Ry an, & Patricia McDonough. (1999). Extracting parity and magnitude from Arabic numerals:Developmental changes in number processing and mental representation. Journal of Experimental Child Psychology, 74(4), 286-308. DOI: 10.1006/jecp.1999.2518. |
| Bonato M., Fabbri S., Umilta C., & Zorzi M. (2007). The mental representation of numerical fractions:real or integer?. Journal of Experimental Psychology:Human Perception and Performance, 33(6), 1410-1419. DOI: 10.1037/0096-1523.33.6.1410. |
| Booth J. L., & Newton K. J. (2012). Fractions:Could they really be the gatekeeper's doorman?. Contemporary Educational Psychology, 37(4), 247-253. DOI: 10.1016/j.cedpsych.2012.07.001. |
| Booth J. L., Newton K. J., & Twissgarrity L. K. (2014). The impact of fraction magnitude knowledge on algebra performance and learning. Journal of Experimental Child Psychology, 118(1), 110-118. |
| Booth J. L., & Siegler R. S. (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology, 42(1), 189-201. DOI: 10.1037/0012-1649.41.6.189. |
| Dehaene S. (1997). The number sense:How the mind creates mathematics. New York: Oxford University Press: 53-76. |
| Dehaene S., & Mehler J. (1992). Cross-linguistic regularities in the frequency of number words. Cognition, 12(1), 119-149. |
| Fazio L. K., Bailey D. H., Thompson C. A., & Siegler R. S. (2014). Relations of different types of numerical magnitude representations to each other and to mathematics achievement. Journal of Experimental Child Psychology, 123(123), 53-72. |
| Girelli L., Lucangeli D., & Butterworth B. (2000). The development of automaticity in accessing number magnitude. Journal of Experimental Child Psychology, 76(2), 104-122. DOI: 10.1006/jecp.2000.2564. |
| Hevia M. D. D., & Spelke E. S. (2009). Spontaneous mapping of number and space in adults and young children. Cognition, 110(2), 198-207. DOI: 10.1016/j.cognition.2008.11.003. |
| Ischebeck A., Schocke M., & Delazer M. (2009). The processing and representation of fractions within the brain:An fmri investigation. Neuroimage, 47(1), 403-413. DOI: 10.1016/j.neuroimage.2009.03.041. |
| Jacob S. N., & Nieder A. (2009). Notation-independent representation of fractions in the human parietal cortex. Journal of Neuroscience the Official Journal of the Society for Neuroscience, 29(14), 4652-4657. DOI: 10.1523/JNEUROSCI.0651-09.2009. |
| Lemaire P., & Lecacheur M. (2002). Children's strategies in computational estimation. Journal of Experimental Child Psychology, 82(4), 281-304. DOI: 10.1016/S0022-0965(02)00107-8. |
| Liu C. H., Xin Z. Q., Lin C. D., & Thompson C. A. (2013). Children's mental representation when comparing fractions with common numerators. Educational Psychology, 33(2), 175-191. DOI: 10.1080/01443410.2012.730324. |
| Liu Y. (2017). Fraction magnitude understanding and its unique role in predicting general mathematics achievement at two early stages of fraction instruction. British Journal of Educational Psychology, 87(5), 1-18. |
| Mullis, I. V. S., Martin, M. O., Foy, P., Olson, J. F., Preuschoff, C., Erberber, E., et al. (2008). TIMSS 2007 international mathematics report: Findings from IEA's trends in international mathematics and science study at the fourth and eighth grades. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College. 31-42. |
| Mullis, I. V. S., Martin, M. O., Foy, P., & Arora, A. (2012). TIMSS 2011 international results in mathematics. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College. 36-50. |
| Opfer J. E., & Devries J. M. (2008). Representational change and magnitude estimation:Why young children can make more accurate salary comparisons than adults. Cognition, 108(3), 843-849. DOI: 10.1016/j.cognition.2008.05.003. |
| Opfer J. E., Thompson C. A., & Devries J. M. (2007). Why children make better estimates of fractional magnitude than adults. Xxix Conference of the Cognitive Science Society., 1361-1366. |
| Schneider M., & Siegler R. S. (2010). Representations of the magnitudes of fractions. Journal of Experimental Psychology Human Perception & Performance, 36(5), 1227-1238. |
| Siegler R. S. (1996). Emerging minds:The process of change in children's thinking. New York:Oxford University Press, 49-83. |
| Siegler R. S., Duncan G. J., Davis-Kean P. E., Duckworth K., Claessens A., & Engel M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691-697. DOI: 10.1177/0956797612440101. |
| Siegler R. S., & Mu Y. (2008). Chinese children excel on novel mathematics problems even before elementary school. Psychological Science, 19(8), 759-763. DOI: 10.1111/j.1467-9280.2008.02153.x. |
| Siegler R. S., & Opfer J. E. (2003). The development of numerical estimation:Evidence for multiple representations of numerical quantity. Psychological Science, 14(3), 237-243. DOI: 10.1111/1467-9280.02438. |
| Siegler R. S., Thompson C. A., & Schneider M. (2011). An integrated theory of whole number and fractions development. Cognitive Psychology, 62(4), 273-296. DOI: 10.1016/j.cogpsych.2011.03.001. |
| Stapel J. C., Hunnius S., Bekkering H., & Lindemann O. (2015). The development of numerosity estimation:Evidence for a linear number representation early in life. Journal of Cognitive Psychology, 27(4), 400-412. DOI: 10.1080/20445911.2014.995668. |
| Stevenson H. W., Chen C., & Uttal D. H. (1990). Beliefs and achievement:A study of black, white, and hispanic children. Child Development, 61(2), 508-523. DOI: 10.2307/1131111. |
| Torbeyns J., Schneider M., Xin Z., & Siegler R. S. (2015). Bridging the gap:Fraction understanding is central to mathematics achievement in students from three different continents. Learning & Instruction, 37(3), 5-13. |
| Van Galen M. S., & Reitsma P. (2008). Developing access to number magnitude:A study of the SNARC effect in 7-to 9-year-olds. Journal of Experimental Child Psychology, 101(2), 99-113. DOI: 10.1016/j.jecp.2008.05.001. |
| Wang Y. Q., & Siegler R. S. (2013). Representations of and translation between common fractions and decimal fractions. Chinese Science Bulletin, 58(36), 4630-4640. DOI: 10.1007/s11434-013-6035-4. |
| Zhou Z., Peverly S. T., & Lin J. (2005). Understanding early mathematical competencies in american and chinese children. School Psychology International, 26(4), 413-427. DOI: 10.1177/0143034305059018. |
| 陈英和. (2015). 儿童数量表征与数概念的发展特点及机制. 心理发展与教育, 31(1), 21-28. |
| 郭红力. (2010)小学高年级儿童的分数数量表征(硕士学位论文). 山东师范大学, 济南. |
| 卢淳, 郭红力, 司继伟, 孙燕. (2014). 不同数字线下儿童与成人分数估计的表征模式. 心理发展与教育, 30(5), 449-456. |
| 孙玉, 司继伟, 黄碧娟. (2016). 分数的数量表征. 心理科学进展, 24(8), 1207-1216. |
| 辛自强, 李丹. (2013). 小学生在非符号材料上的分数表征方式. 心理科学, 36(2), 364-371. |
| 张帆, 赖颖慧, 陈英和. (2015). 儿童数字线表征的发展——心理长度的影响. 心理发展与教育, 31(2), 149-156. |
| 张丽, 卢彩芳, 杨新荣. (2014). 3~6年级儿童整数数量表征与分数数量表征的关系. 心理发展与教育, 30(1), 1-8. |
| 张丽, 辛自强, 王琦, 李红. (2012). 整数构成对分数加工的影响. 心理发展与教育, 28(1), 31-38. |
| 周广东, 莫雷, 温红博. (2009). 儿童数字估计的表征模式与发展. 心理发展与教育, 25(4), 21-29. |
 2018, Vol. 34
2018, Vol. 34


