国家教育部主管、北京师范大学主办。
文章信息
- 顾红磊, 温忠麟. 2017.
- GU Honglei, WEN Zhonglin. 2017.
- 多维测验分数的报告与解释:基于双因子模型的视角
- Reporting and Interpreting Multidimensional Test Scores:A Bi-factor Perspective
- 心理发展与教育, 33(4): 504-512
- Psychological Development and Education, 33(4): 504-512.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2017.04.15
2. 华南师范大学心理应用研究中心/心理学院, 广州 510631
2. Center for Studies of Psychological Application/School of Psychology, South China Normal University, Guangzhou 510631
多维测验(multidimensional test)是指一份测验包含了多个不同而又相互关联的维度或分测验。例如,在智力领域,韦氏成人智力量表(Wechsler Adult Intelligence Scale, WAIS)是一个多维量表,它由言语理解能力(Verbal Comprehension, VC),知觉推理能力(Perceptual Reasoning, PR),工作记忆能力(Working Memory, WM)和加工速度能力(Processing Speed, PS)构成(Wechsler, 2008)。再如,在人格领域,马基雅维利主义人格量表(Machiavellianism Personality Scale, MPS)包括不道德操纵、控制欲、地位欲和不信任他人四个维度(Dahling, Whitaker, & Levy, 2009)。在多维测验中,通常各个维度不可以相互替换,而且每个维度与其他变量的关系不同。
尽管多维测验的使用越来越普遍,但应用工作者仍存在一些迷惑不解的问题:何时可以报告多维测验的总分?何时可以报告分测验分数?报告总量表的信度还是分量表的信度?在控制总分的影响后,分测验分数还能提供额外的有价值的信息吗?什么时候多维测验数据可以用单维模型去拟合?
本文将针对以上问题展开论述,首先对多维测验的一般建模方法进行回顾和评介,其次概述基于双因子模型(bi-factor model)计算得到的统计指标,然后总结出两个兼顾简洁性和精确性的多维测验分析流程,明确如何报告多维测验的信度,如何报告和解释多维测验分数,如何利用多维建模进行结构模型分析。最后通过一个实例进行演示。
1 多维测验建模方法一般来说,多维测验建模方法可以分为两大类,一类使用显变量,另一类使用潜变量。
1.1 显变量建模总分法(total score approach)假定各维度的权重相同,不考虑维度之间的差异,将整个构念作为研究对象,合成整份测验的总分或平均分,然后研究整个构念与其他变量的关系。
总分法主要有三个优点:(1) 概念简单,容易计算;(2) 由于整个测验比任何一个维度包含的题目数都要多,因此总分法得到的量表信度通常比较高;(3) 总分法覆盖的内容范畴比任何一个维度都要宽泛,因此比单个维度提供更高的内容效度(Carmines & Zeller, 1979)。总分法最大的不足在于提供的信息有限,无法知晓各维度与其他变量的具体关系。用量表总分或平均分来预测结果变量时,会遮掩许多有价值的信息。例如,哪些维度的预测效应显著,哪些维度的预测效应不显著。如果几个维度与结果变量的关系刚好相反,则研究者可能得出零效应的错误结论(Hull, Lehn, & Tedlie, 1991)。
分量报告法(individual score approach)将各维度作为研究对象,合成每个维度的总分或平均分,然后分别探讨各维度与其他变量的关系。分量报告法可以单独检验各个维度对结果变量的预测效应,在一定程度上弥补了总分法的不足。分量报告法的主要缺点在于无法分离各维度的特殊效应与共同效应,二者容易发生混淆(Chen, Hayes, Carver, Laurenceau, & Zhang, 2012)。此外,当使用几个相关较高的维度预测结果变量时,可能存在多重共线性问题(Cole & Preacher, 2014)。
总之,总分法和分量报告法在测量多维构念时,往往顾此失彼,无法同时检验各维度的共同效应和独特效应。此外,两种方法都是基于显变量的分析方法,无法控制测量误差,因此得到的参数估计值可能与真值之间存在一定的偏差(侯杰泰, 温忠麟, 成子娟, 2004; 温忠麟, 刘红云, 侯杰泰, 2012)。
1.2 潜变量建模下面以韦氏成人智力量表(WAIS)为例,比较各种测量模型的差异。
1.2.1 单维模型单维模型是和总分法对应的验证性因子分析(confirmatory factor analysis, CFA)模型,它把整个构念作为因子(潜变量),把所有题目作为观测指标。
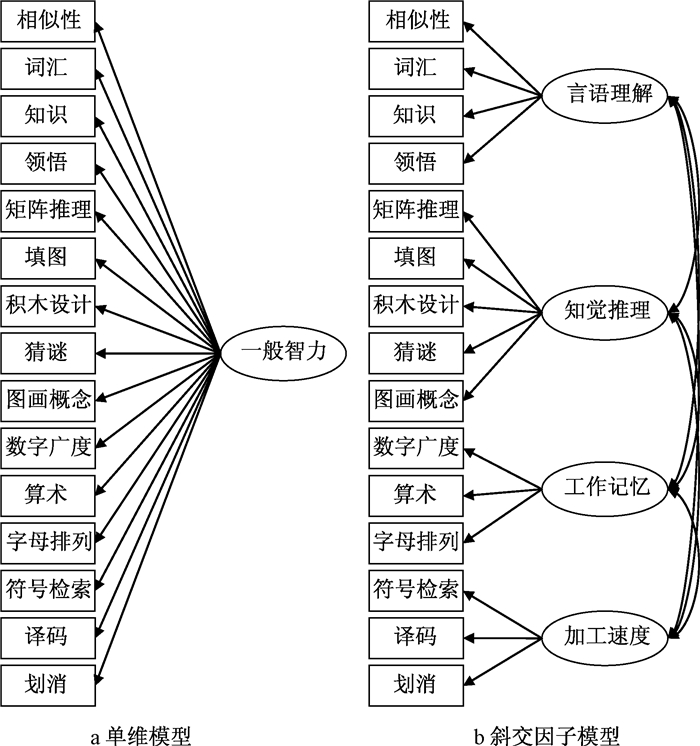
如图 1a所示,一般智力(整体构念)作为唯一的因子,直接定义在相似性、词汇、知识等15个观测分数上。
|
| 图 1 单维模型和斜交因子模型 |
和总分法一样,单维模型简单易行,但无法反映各维度与其他变量的关系。
1.2.2 斜交因子模型斜交因子模型(见图 1b)是和分量报告法对应的CFA模型,它把各个维度作为因子,相应的题目作为观测指标,用因子相关来反映维度之间的共变性,因此斜交因子模型又称作“相关特质模型”。
同分量报告法一样,尽管斜交因子模型可以单独检验各维度的独特效应,但无法对维度之间的共同效应进行分析。
1.2.3 高阶因子模型如果维度之间高度相关,并且可以形成一个有实质意义的整体构念(例如,一般智力),则可以建立高阶因子模型(higher-order factor model),常用的是二阶因子模型。
高阶因子模型(如图 2c所示)假定每个一阶因子(言语理解、知觉推理、工作记忆和加工速度)同时受到两个因素的直接影响:一个是代表一般智力(G因子)的二阶因子,它可以解释维度之间的共同变异;另一个是一阶因子(被二阶因子解释后)的残差(ζ),它可以解释各个维度的特殊变异。

|
| 图 2 高阶因子模型和双因子模型 |
高阶因子模型中一阶因子和题目的关系与斜交因子模型中各维度与题目的关系相同(即因子负荷对应相等),并且高阶因子模型中任意两个二阶因子负荷的乘积都等于斜交因子模型中对应维度之间的协方差(例如,γ1γ2=cov(VC, PR))。
当模型中只有3个一阶因子时(共有3个相关),二阶因子模型和斜交因子模型的拟合指标完全等同。当模型中一阶因子的个数超过3个时,二阶因子模型需要估计的参数较少,因此比斜交因子模型简约(侯杰泰等, 2004)。
尽管高阶因子模型分离了各维度的共同效应(用高阶因子负荷表示)和特殊效应(用低阶因子的残差表示),但过于强调维度之间的共同性,妨碍了对维度独特性的研究。另外,高阶因子并非定义在观测变量上,而是定义在低阶因子上,看起来难以捉摸,高阶因子负荷的解释含糊不清(Gignac, 2008)。
1.2.4 双因子模型双因子模型(如图 2d所示)假定:(1) 存在一个全局因子(general factor;例如,一般智力因子)可以解释所有题目的共同变异;(2) 存在多个局部因子(specific factor;例如,特殊能力因子),控制了全局因子的影响后,每个局部因子可以额外解释部分题目的共同变异(Chen, West, & Sousa, 2006)。
若一份多维测验由p个题目x1, x2, …, xp组成,测量了一个全局因子G和n个局部因子F1, F2, …, Fn,则题目xi可以表示为(叶宝娟, 温忠麟, 2012):

|
(1) |
其中,ai是题目xi在全局因子G上的负荷,bij是题目xi在局部因子Fj上的负荷,δi是题目xi的测验误差。通常假设全局因子、局部因子和误差互不相关(Chen et al., 2012)。
双因子模型整合了多维测验的单维性和多维性,可以同时检验各维度的共同效应和独特效应,近年来被研究者广泛应用于人格心理学(Armon & Shirom, 2011)、教育心理学(Wang, Fredricks, Ye, Hofkens, & Linn, 2016)、管理心理学(Mészáros, Ádám, Szabó, Szigeti, & Urbán, 2014)、临床心理学(Caci, Morin, & Tran, 2015)、犯罪心理学(Hyland, 2015)、运动心理学(Cornick, 2015)等领域。
2 基于双因子模型的统计指标不难发现,如果将双因子模型中的局部因子负荷固定为0,则可以得到单维模型。如果将双因子模型中的全局因子负荷固定为0,并且允许局部因子之间的相关自由估计,那么可以得到斜交因子模型。因此,单维模型和斜交因子模型都是双因子模型的特例。高阶因子模型也是双因子模型的特例(Reise, 2012; 顾红磊, 温忠麟, 方杰, 2014):如果将高阶因子换作全局因子,全局因子的负荷等于一阶因子负荷和二阶因子负荷的乘积;一阶因子被二阶因子解释后的残差变成了局部因子。因此,可以最一般地以双因子模型为基准,构建与多维构念测量有关的统计指标。
2.1 共同变异解释比根据双因子模型的测量方程(1),可以计算出全局因子解释的变异占共同因子变异的比例(explained common variance, ECV):
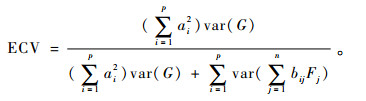
|
(2) |
ECV反映了全局因子相对于全部因子的强度,即多维测验单维倾向性的程度。ECV取值在0和1之间,ECV越大,测验越单维。当ECV足够大时(例如,ECV > 0.7),用单维模型拟合多维测验数据产生的参数估计值(例如,全局因子负荷、路径系数)偏差较小,可以接受(Reise, 2012)。
2.2 未受影响的相关比例研究表明,使用单维模型拟合多维数据产生的参数估计值偏差,不仅与ECV直接有关,而且二者的关系还受到未受影响的相关比例(percentage of uncontaminated correlations, PUC)的调节(Bonifay, Reise, Scheines, & Meijer, 2015; Reise, Scheines, Widaman, & Haviland, 2013)。PUC反映了双因子模型中,题目相关仅受全局因子影响的程度,等于1减去同属于一个局部因子的题目之间的相关系数的个数与所有题目相关系数的个数的比例:

|
(3) |
其中,pj表示第j个局部因子包含的题目个数,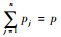
① 一份12题的多维测验,每3个题目测量一个维度,则整份测验测量了1个全局因子和4个局部因子。该测验共包含[(12×11)/2]=66个题目相关系数。同一个局部因子内题目之间的相关同时受到全局和局部因子变异的影响,这样的相关共有[(3×2)/2]×4=12个。来自不同局部因子的题目之间的相关只反映了全局因子变异,共有66-12=54个未同时受全局和局部因子变异影响的相关,则PUC=54/66=0.82。
一般来说,当PUC足够大时(例如,PUC > 0.7),即使ECV不高,用单维模型拟合多维测验数据也能得到相对无偏的参数估计值。当PUC不够大时,只有ECV足够高(例如,ECV > 0.7),用单维模型拟合多维测验数据的偏差才可以忽略不计。如果PUC和ECV都不高,那么使用单维模型拟合多维数据的偏差就很大,应该选用双因子模型(Rodriguez, Reise, & Haviland, 2016a)。
2.3 信度系数基于双因子结构,可以计算四类信度系数:总量表合成信度、同质性系数、分量表合成信度和分量表残差化信度(Rodriguez et., 2016a)②。
② ECV和四类信度系数可以通过Mplus程序得到,见附录;PUC可以手算,计算过程见脚注①。
2.3.1 总量表合成信度总量表合成信度(composite reliability, 用ω表示),又称作是内部一致性信度,反映了所有题目之间的相关性,大小等于全局因子分数方差和所有局部因子分数方差之和占测验分数方差的比例(Rodriguez, Reise, & Haviland, 2016b; 温忠麟, 叶宝娟, 2011),则

|
(4) |
一般认为,当ω在0.7以上时,表明多维测验合成分数的可靠性可以接受(Bentler, 2009)。
2.3.2 同质性系数同质性系数(homogeneity coefficient, 用ωH表示),反映了所有题目测量相同特质的程度,大小等于全局因子分数方差占测验分数方差的比例(Rodriguez et al., 2016b; 叶宝娟, 温忠麟, 2012):
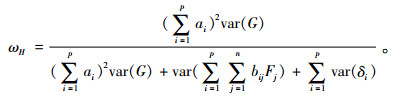
|
(5) |
ωH越大,测验越同质。一般来说,当ωH > 0.5时(全局因子分数和测验总分的相关系数大致为0.7,属于高相关),可以认为同质性较高,合成整份测验总分有意义(温忠麟, 叶宝娟, 印刷中)。ωH随着测验长度、全局因子负荷和PUC的增大而增大(Rodriguez et al., 2016a)。
ECV和ωH的区别在于,ECV反映的是数据的单维程度(即全局因子的强度),而ωH表示的是用测验总分反映单个公共因子的程度(即全局因子的饱和度)。显然,如果同质性系数高,ECV一定高;反之不然——某个测验具有完美的单维结构,但如果测量误差很大,那么合成测验总分也是没有意义的。因此,ECV大,ωH不一定高。特别地,如果是单维,ECV变成1,而同质性系数ωH(此时等于合成信度ω)未必高。
2.3.3 分量表合成信度如果只考虑第j个局部因子Fj内题目(记为x1, x2, …, xpj)对应的负荷和误差,则可以得到分量表的合成信度(用ωSj表示),
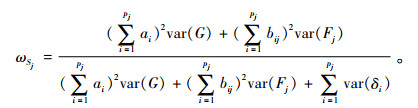
|
(6) |
ωSj越高,表明分量表合成分数的可靠性越高。
2.3.4 分量表残差化信度对于多维测验,除了报告量表总分对目标构念变异的解释程度(即同质性系数)以及总的测验信度(即合成信度),还可以计算控制了全局因子的影响后,第j个局部因子额外解释的变异占该分量表分数变异的比例,即分量表残差化信度(residualized subscale reliability, ωRSj; Reise, 2012):
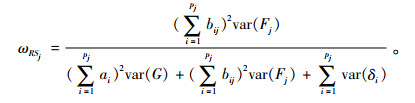
|
(7) |
当ωSj和ωRSj相差较大时(ωRSj/ωSj < 0.7),表明分测验的变异主要是由全局因子贡献的,局部因子解释的变异较少,因此计算和报告分量表分数没有实质意义;当ωSj和ωRSj相差较小时(ωRSj/ωSj > 0.7),表明分测验的变异主要是由局部因子贡献的,因此计算和报告分量表分数合理(Gu, Wen, & Fan, 2017a; Reise, Bonifay, & Haviland, 2013)。
值得注意的是,信度的计算公式中,涉及的负荷是先求和后平方,这是因为信度是从合成分数为出发点,去分解和计算各种方差;而ECV计算公式中涉及的负荷是先平方后求和,这是因为ECV是以合并各题目的公共因子方差之和为出发点,去计算全局因子的方差所占的比例。
3 多维测验分数报告根据前面的讨论,本文提出一个“自上而下”(从总测验到分测验)的多维测验分数报告的流程。
首先,建立双因子模型,计算同质系数、分量表合成信度和分量表残差化信度。
然后,按照以下四种情况进行多维测验分数的报告:
(1) 如果ωH足够大(大于0.5),ωSj足够高(大于0.7),并且ωSj和ωRSj相差较小(后者与前者的比值大于0.7),则同时报告测验总分和分测验分数都有意义;
(2) 如果ωH足够大(超过0.5),但ωSj低(小于0.7) 或者ωSj和ωRSj相差较大(后者与前者的比值低于0.7),则只报告测验总分;
(3) 如果ωH偏低(小于0.5),ωSj足够高(大于0.7),则只报告分测验分数;
(4) 其余情况,报告测验总分或分测验分数没有多少意义。
4 包含多维测验变量的统计建模如果研究者在多维测验分数的基础上,要进一步探讨多维构念与其他变量的关系,则可以依据图 3所示的流程,决定建立什么样的测量模型作为统计分析模型的组成部分:

|
| 图 3 多维测验建模流程 |
第一步,建立双因子模型。如果PUC足够高,则建立单维模型。否则,继续检验ECV;
第二步,检验ECV。如果ECV足够大,则建立单维模型。否则,建立双因子模型。
5 示例接下来用一个实际例子演示如何通过双因子建模对多维测验分数进行报告和解释。本例要探究的是马基雅维利主义人格量表(MPS)的因子结构以及如何报告该量表的分数。数据来自219名企业员工,被试年龄在17岁至51岁之间(M=26.52, SD=4.63),平均工作年限为48个月。先将题目得分进行标准化,然后使用Mplus 7.0软件建立双因子模型(Mplus程序见附录)。结果表明,χ2=201.7,df=88,CFI=0.91,RMSEA=0.077,SRMR=0.06,基本达到了良好拟合的标准。
最后,基于双因子模型,计算有关统计指标。由表 1可知,整份量表的合成信度(ω)为0.91,各分量表的合成信度(ωSj)在0.73和0.81之间,表明总量表和分量表信度均不低于0.7,达到了心理测量学的标准。同质系数(ωH)为0.77,在0.5以上,因此在本研究中,报告MPS的总分是有意义的。四个分量表的残差化信度(ωRSj)分别为0.24、0.46、0.38和0.32,各占分量表合成信度的29.6%、56.8%、47.5%和43.8%,表明在控制了全局因子的影响后,局部因子对分量表分数的贡献处于中下水平,因此在报告MPS总分的基础上,报告四个分量表得分没有意义。需要说明的是,以往研究者报告的分量表分数实际上同时包含共同效应和独特效应。较好的做法是通过建立双因子模型将题目变异分解为各维度的共同效应(全局因子解释的变异)和各维度的独特效应(局部因子解释的变异)。当各维度的共同效应较小时,可以把双因子模型简化为斜交因子模型,传统的分析方法才有意义。
| 题目 | 单维模型 | 双因子模型 | |||||||
| Mach | Mach | 不道德操纵 | 控制欲 | 地位欲 | 不信任他人 | ECV | PUC | ||
| x1 | 0.61 | 0.59 | 0.63 | ||||||
| x2 | 0.46 | 0.46 | 0.42 | ||||||
| x3 | 0.47 | 0.46 | 0.24 | ||||||
| x4 | 0.61 | 0.61 | 0.27 | ||||||
| x5 | 0.59 | 0.72 | 0.26 | ||||||
| x6 | 0.56 | 0.53 | 0.30 | ||||||
| x7 | 0.54 | 0.41 | 0.66 | ||||||
| x8 | 0.66 | 0.53 | 0.74 | ||||||
| x9 | 0.58 | 0.44 | 0.55 | ||||||
| x10 | 0.65 | 0.59 | 0.46 | 0.54 | 0.78 | ||||
| x11 | 0.69 | 0.60 | 0.53 | ||||||
| x12 | 0.57 | 0.63 | 0.04a | ||||||
| x13 | 0.32 | 0.38 | 0.28 | ||||||
| x14 | 0.23 | 0.20 | 0.26 | ||||||
| x15 | 0.49 | 0.48 | 0.51 | ||||||
| x16 | 0.47 | 0.46 | 0.78 | ||||||
| ω(ωSj) | 0.91 | 0.81 | 0.81 | 0.80 | 0.73 | ||||
| ωH(ωRSj) | 0.77 | 0.24 | 0.46 | 0.38 | 0.32 | ||||
| 注:a表示p > 0.05。 | |||||||||
此外,在本研究中,ECV在0.7以下(ECV=0.54),PUC超过了0.7(PUC=0.78)。与双因子模型中的全局因子负荷相比,单维模型因子负荷的平均相对偏差为6.3%(相对偏差等于单维模型因子负荷与全局因子负荷的差值除以全局因子负荷),在10%以内,可以接受(Muthén, Kaplan, & Hollis, 1987)。由此表明,如果要使用MPS进行后续分析(例如,探讨马基雅维利主义人格与亲社会行为的关系),可以忽略局部因子(不道德操纵等分量表)的影响,用简单的单维模型(将马基雅维利主义人格作为因子,原始题目或者按照维度打包后的题目包作为指标)拟合MPS数据,然后建立马基雅维利主义人格和其他变量之间的路径关系。
6 讨论在心理和教育测量中,经常涉及多维测验分数如何报告和解释,以及多维测验如何建模等议题。一般的做法是先在SPSS里计算总测验及分测验的克伦巴赫α系数,如果α系数高,表明总测验及分测验信度高,然后合成测验总分和分测验得分,进行后续分析。这种做法无法厘清测验总分和分测验分数的变异来源,常常误导研究者得出错误的结论(Rodriguez et al., 2016b)。本文基于双因子模型的视角,提供了多维测验分数报告和解释以及多维测验建模的流程,不仅可以让读者明确如何正确报告和解释测验总分和分测验分数,而且还为如何使用多维测验进行下一步统计分析带来一些启示。
概括的说,是否使用测验总分和分测验分数,看同质性系数、分测验合成信度和分测验残差化信度。当同质性系数足够大(在0.5以上)时,可以报告测验总分。当某个分量表的合成信度足够高而且和残差化信度相差较小时,可以报告该分测验的分数。
是否建立单维模型,不应该看单维模型是否拟合良好,而应该看由PUC和ECV决定的参数估计值相对偏差。即便单维模型拟合不佳,只要PUC和ECV至少有一个足够高,就可以在进行后续分析时将多维构念当做单维构念处理,此时研究者可以采用两种方法建立单维模型:一是把整个构念作为因子,把题目作为指标;二是先采用内部一致性策略(internal-consistency approach)将每个维度打成一个题目包(item parcel),然后把整个构念作为因子,把维度作为指标进行结构模型分析(Rodriguez et al., 2016b; 吴艳, 温忠麟, 2011)。
需要指出的是,当全局因子和局部因子其中有一个是方法因子时(即该因子解释的变异是由测量方法引起的、与测量构念无关的系统变异),使用本文提出的两个流程也是有意义的。如果全局因子是方法因子,那么它代表的可能是共同方法偏差(Henry, Gorman-Smith, Schoeny, & Tolan, 2014; Lilleoja, Dobewall, Aavik, Strack, & Verkasalo, 2016),此时合成测验总分没有意义,研究者不需考虑同质系数,只需通过计算分测验合成信度和残差化信度判断是否可以合成分测验分数。当PUC和ECV至少有一个很高时,表明测验受共同方法偏差的影响较大,则研究者在进行其他分析时必须通过建立双因子模型对共同方法偏差进行统计控制;当二者都低时,研究者可以忽略共同方法偏差的影响,直接建立斜交因子模型。
如果局部因子是方法因子,那么它反映的可能是项目表述效应(即由项目表述方式的差异引起的与测量内容无关的系统变异; Gu, Wen, & Fan, 2015, 2017b; 顾红磊, 王才康, 2012; 顾红磊, 温忠麟, 2014),此时报告分量表分数没有意义,研究者不用考虑分量表信度,只需通过计算同质系数判断是否可以合成测验总分。当PUC和ECV至少有一个很高时,研究者可以忽略项目表述效应的影响,直接建立单维模型;当二者都低时,表明测验受项目表述效应的影响较大,则研究者在进行其他分析时必须通过建立双因子模型对项目表述效应进行统计控制。
一般来说,如果研究者对多个不同的变量建立双因子模型,那么全局因子代表的应该是方法因子(例如,共同方法偏差);如果研究者对包含多个维度的单个变量建立双因子模型,那么作为一种统计建模方法,双因子模型本身无法区分全局因子是特质因子还是方法因子。要解释全局因子是否有实质含义,关键在于研究者在分析测量模型之前,要有坚实的理论基础作为支撑(例如,明确合成多维测验总分是否有意义)。此外,局部因子是特质因子还是方法因子,和量表本身的特性有关。例如,如果研究者采用的量表既有正向题又有反向题,并且正向题和反向题分别对应不同的局部因子,那么局部因子代表的应该是项目表述效应方法因子。
附录:MPS双因子模型的mplus程序Title: Bi-factor Model of MPS
Data: File is p.dat; !假设所有变量为标准化变量
VARIABLE: NAMES ARE x1-x16;
MODEL: G by x1-x16* (b1-b16);
F1 by x1-x5* (c1-c5);! F1为不道德操纵局部因子
F2 by x6-x8* (c6-c8);! F2为控制欲局部因子
F3 by x9-x11* (c9-c11);! F3为地位欲局部因子
F4 by x12-x16* (c12-c16);! F4为不信任他人局部因子
G @ 1; F1-F4 @ 1;
x1-x16 (p1-p16);
G WITH F1-F4 @ 0; F1-F4 WITH F1-F4 @ 0;
MODEL constraint: NEW (H1-H47);
H1=b1+b2+b3+b4+b5; H2=b6+b7+b8; H3=b9+b10+b11;H4=b12+b13+b14+b15+b16;
H5=c1+c2+c3+c4+c5; H6=c6+c7+c8; H7=c9+c10+c11;H8=c12+c13+c14+c15+c16;
H9=p1+p2+p3+p4+p5; H10=p6+p7+p8; H11=p9+p10+p11; H12=p12+p13+p14+p15+p16;
H13=H1+H2+H3+H4; H14=H9+H10+H11+H12;
H15=H1^2; H16=H2^2; H17=H3^2; H18=H4^2;
H19=H5^2; H20=H6^2; H21=H7^2; H22=H8^2; H23=H13^2;
H24=H19+H20+H21+H22+H23; H25=H24+H14;
H26=H24/H25;!计算总量表合成信度
H27=H23/H25;!计算总量表同质性系数
H28=H15+H19; H29=H28+H9;
H30=H28/H29;!计算不道德操纵分量表合成信度
H31=H19/H29;!计算不道德操纵分量表残差化信度
H32=H16+H20; H33=H32+H10;
H34=H32/H33;!计算控制欲分量表合成信度
H35=H20/H33;!计算控制欲分量表残差化信度
H36=H17+H21; H37=H36+H11;
H38=H36/H37;!计算地位欲分量表合成信度
H39=H21/H37;!计算地位欲分量表残差化信度
H40=H18+H22; H41=H40+H12;
H42=H40/H41;!计算不信任他人分量表合成信度
H43=H22/H41;!计算不信任他人分量表残差化信度
H44=b1^2+b2^2+b3^2+b4^2+b5^2+b6^2+b7^2+b8^2+b9^2+b10^2+b11^2+b12^2+b13^2
+b14^2+b15^2+b16^2;
H45=c1^2+c2^2+c3^2+c4^2+c5^2+c6^2+c7^2+c8^2+c9^2+c10^2+c11^2+c12^2+c13^2
+c14^2+c15^2+c16^2;
H46=H44+H45;
H47=H44/H46;!计算ECV
OUTPUT: stdyx;
| Armon G., & Shirom A. (2011). The across-time associations of the five-factor model of personality with vigor and its facets using the bifactor model. Journal of Personality Assessment, 93, 618-627. DOI: 10.1080/00223891.2011.608753. |
| Bentler P. M. (2009). Alpha, dimension-free, and model-based internal consistency reliability. Psychometrika, 74, 137-143. DOI: 10.1007/s11336-008-9100-1. |
| Bonifay W. E., Reise S. P., Scheines R., & Meijer R. R. (2015). When are multidimensional data unidimensional enough for structural equation modeling? An evaluation of the DETECT multidimensionality index. Structural Equation Modeling, 22, 504-516. DOI: 10.1080/10705511.2014.938596. |
| Caci H., Morin A. J., & Tran A. (2015). Investigation of a bifactor model of the strengths and difficulties questionnaire. European Child & Adolescent Psychiatry, 24, 1291-1301. |
| Carmines, E. G., & Zeller, R. A. (1979). Reliability and validity assessment. Beverly Hills, CA:Sage. https://www.amazon.com/Reliability-Validity-Assessment-Quantitative-Applications/dp/0803913710 |
| Chen F. F., Hayes A., Carver C. S., Laurenceau J. P., & Zhang Z. (2012). Modeling general and specific variance in multifaceted constructs:A comparison of the bifactor model to other approaches. Journal of Personality, 80, 219-251. DOI: 10.1111/jopy.2012.80.issue-1. |
| Chen F. F., West S. G., & Sousa K. H. (2006). A comparison of bifactor and second-order models of quality of life. Multivariate Behavioral Research, 41, 189-225. DOI: 10.1207/s15327906mbr4102_5. |
| Cole D. A., & Preacher K. J. (2014). Manifest Variable Path Analysis:Potentially Serious and Misleading Consequences Due to Uncorrected Measurement Error. Psychological Methods, 19, 300-315. DOI: 10.1037/a0033805. |
| Cornick J. E. (2015). Factor Structure of the Exercise Self-Efficacy Scale. Measurement in Physical Education and Exercise Science, 19, 208-218. DOI: 10.1080/1091367X.2015.1074579. |
| Dahling J. J., Whitaker B. G., & Levy P. E. (2009). The development and validation of a new Machiavellianism scale. Journal of Management, 35, 219-257. |
| Gignac G. E. (2008). Higher-order models versus direct hierarchical models:g as superordinate or breadth factor?. Psychology Science Quarterly, 50, 21-43. |
| Gu H., Wen Z., & Fan X. (2015). The Impact of Wording Effect on Reliability and Validity of the Core Self-Evaluation Scale (CSES):A Bi-factor Perspective. Personality and Individual Difference, 83, 142-147. DOI: 10.1016/j.paid.2015.04.006. |
| Gu H., Wen Z., & Fan X. (2017a). Structural validity of the Machiavellian Personality Scale:A bifactor exploratory structural equation modeling approach. Personality and Individual Differences, 105, 116-123. DOI: 10.1016/j.paid.2016.09.042. |
| Gu H., Wen Z., & Fan X. (2017b). Examining and Controlling for Wording Effect in a Self-Report Measure:A Monte Carlo Simulation Study. Structural Equation Modeling:A Multidisciplinary Journal, 24, 545-555. DOI: 10.1080/10705511.2017.1286228. |
| Henry D., Gorman-Smith D., Schoeny M., & Tolan P. (2014). "Neighborhood Matters":Assessment of Neighborhood Social Processes. American Journal of Community Psychology, 54, 187-204. DOI: 10.1007/s10464-014-9681-z. |
| Hull J. G., Lehn D. A., & Tedlie J. C. (1991). A general approach to testing multifaceted personality constructs. Journal of Personality and Social Psychology, 61, 932-945. DOI: 10.1037/0022-3514.61.6.932. |
| Hyland P. (2015). Application of bifactor models in criminal psychology research:a guide to researchers. Journal of Criminal Psychology, 5, 65-74. DOI: 10.1108/JCP-03-2015-0011. |
| Lilleoja L., Dobewall H., Aavik T., Strack M., & Verkasalo M. (2016). Measurement equivalence of Schwartz's refined value structure across countries and modes of data collection:New evidence from Estonia, Finland, and Ethiopia. Personality and Individual Differences, 102, 204-210. DOI: 10.1016/j.paid.2016.07.009. |
| Mészáros V., Ádám S., Szabó M., Szigeti R., & Urbán R. (2014). The Bifactor Model of the Maslach Burnout Inventory-Human Services Survey (MBI-HSS)-An Alternative Measurement Model of Burnout. Stress and Health, 30, 82-88. DOI: 10.1002/smi.v30.1. |
| Muthén B. O., Kaplan D., & Hollis M. (1987). On structural equation modeling with data that are not missing completely at random. Psychometrika, 52, 431-462. DOI: 10.1007/BF02294365. |
| Reise S. P. (2012). The rediscovery of bifactor measurement models. Multivariate Behavioral Research, 47, 667-696. DOI: 10.1080/00273171.2012.715555. |
| Reise S. P., Bonifay W. E., & Haviland M. G. (2013). Scoring and modeling psychological measures in the presence of multidimensionality. Journal of Personality Assessment, 95, 129-140. DOI: 10.1080/00223891.2012.725437. |
| Reise S. P., Scheines R., Widaman K. F., & Haviland M. G. (2013). Multidimensionality and structural coefficient bias in structural equation modeling:A bifactor perspective. Educational and Psychological Measurement, 1, 5-26. |
| Rodriguez A., Reise S. P., & Haviland M. G. (2016a). Applying Bifactor Statistical Indices in the Evaluation of Psychological Measures. Journal of Personality Assessment, 98, 223-237. DOI: 10.1080/00223891.2015.1089249. |
| Rodriguez A., Reise S. P., & Haviland M. G. (2016b). Evaluating Bifactor Models:Calculating and Interpreting Statistical Indices. Psychological Methods, 21, 137-150. DOI: 10.1037/met0000045. |
| Wang M. T., Fredricks J. A., Ye F., Hofkens T. L., & Linn J. S. (2016). The Math and Science Engagement Scales:Scale development, validation, and psychometric properties. Learning and Instruction, 43, 16-26. DOI: 10.1016/j.learninstruc.2016.01.008. |
| Wechsler, D. (2008). Wechsler Adult Intelligence Scale-Fourth Edition. San Antonio, TX:Pearson Assessment. http://www.statisticssolutions.com/wechsler-adult-intelligence-scale-fourth-edition-wais-iv/ |
| 顾红磊, 王才康. (2012). 项目表述效应的统计控制:以中文版生活定向测验为例. 心理科学, 35, 1247-1253. |
| 顾红磊, 温忠麟. (2014). 项目表述效应对自陈量表信效度的影响——以核心自我评价量表为例. 心理科学, 37, 1245-1252. |
| 顾红磊, 温忠麟, 方杰. (2014). 双因子模型:多维构念测量的新视角. 心理科学, 37, 973-979. |
| 侯杰泰, 温忠麟, 成子娟. (2004). 结构方程模型及其应用. 北京: 教育科学出版社. |
| 温忠麟, 刘红云, 侯杰泰. (2012). 调节效应和中介效应分析. 北京: 教育科学出版社. |
| 温忠麟, 叶宝娟. (2011). 测验信度估计:从α系数到内部一致性信度. 心理学报, 43, 821-829. |
| 温忠麟, 叶宝娟. (印刷中). 多变量分析热点: 中介效应和调节效应. 见莫雷, 刘鸣(主编). 当代心理学研究. 北京: 科学出版社. |
| 吴艳, 温忠麟. (2011). 结构方程建模中的题目打包策略. 心理科学进展, 19, 1859-1867. |
| 叶宝娟, 温忠麟. (2012). 测验同质性系数及其区间估计. 心理学报, 44, 1687-1694. |
 2017, Vol. 33
2017, Vol. 33


