国家教育部主管、北京师范大学主办。
文章信息
- 赵琪, 李龙凤, 邓之君, 陈英和. 2017.
- ZHAO Qi, LI Longfeng, DENG Zhijun, CHEN Yinghe. 2017.
- 数量空间表征的特点:跨视听通道下的SNARC效应
- Characteristics of the Spatial Representation of Magnitude:SNARC Effect across Audiovisual Channels
- 心理发展与教育, 33(2): 129-138
- Psychological Development and Education, 33(2): 129-138.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2017.02.01
数量表征指主体对数量概念及其关系理解的概念系统(陈英和,赖颖慧,2013),是数认知过程中重要的一个环节。由于数量加工离不开客体的参与,而每一个客体都存在空间上的特性,所以抽象于客体之上,对数字的编码与空间信息的加工直接存在着某些关联。在Dehaene等人(1993)的经典研究中发现,在数字大小判断和奇偶判断等任务中,右手对大数的反应更快,左手对小数的反应更快,即数字的表征具有空间特性。数字大小与空间表征之间的这种对应关系称为空间数字联合反应编码效应,简称为SNARC(Spatial Numerical Association of Response Codes)效应(Dehaene,Bossini,& Giraux,1993)。后续大量研究证明数量空间表征广泛而稳定存在(Wood,Willmes,Nuerk,& Fischer,2008)。
大量研究发现,SNARC效应不仅稳定存在于不同刺激形式的加工过程中(Fisher,Riello,Giordano,& Rusconi,2013;Lidji,Kolinsky,& Lochy,2007;Previtali,de Hevia,& Girelli,2010),也广泛存在于不同通道的加工过程中(孔风,赵晶晶,游旭群,张宇,2012;Golob,Lewald,Jungilligens,& Getzmann,2016;Nuerk,Wood,& Willmes,2005)。孔风等人(2012)在研究中采用听觉条件下呈现负数材料,结果发现了稳定的数量空间表征。然而以往大部分研究只证实了SNARC效应的加工通道广泛性,很少有研究直观地对比两个通道的数量空间表征加工是否存在差异。在Nuerk等人的研究(2005)中发现,个体虽然对不同通道呈现的数字的反应时存在较大差异(听觉通道下数字的平均反应时为909ms,视觉通道下数字的平均反应时为574ms),但在不同通道下的SNARC效应值却不存在显著差异(听觉通道下SNARC效应大小为3.58,视觉的SNARC效应大小为3.02)。但是,Szucs等人(2004)在SNARC效应的ERP研究中发现,听觉刺激和视觉刺激引起的SNARC效应在N100和P400这两个脑电成份上差异显著。这个结果指出SNARC效应在听觉通道和视觉通道下的机制可能存在差异。那么,这两个通道的SNARC效应是否会存在差异是本研究想要关注的重点之一。
在现实世界中,信息往往以多种模式存在,因此人类的大脑也需要依靠不同的感官系统来获得信息。在生活中,往往单一通道的刺激模式不能产生足够的感觉信息,大脑更多的是以多通道感觉整合的模式来对外界的刺激进行感知和反应。在多感觉整合过程中,视觉和听觉是人类感知信息的最主要通道,二者在大脑中的整合也在准确感知外界刺激的过程中发挥着重要作用(Durk,Daniel,Salvador,& Marty,2010;Stein & Stanford,2008),因此,探究视觉和听觉以及二者的交互作用具有极重要的意义,也吸引了很多研究者的注意。已有研究发现,不同通道间的信息会相互影响,多通道的信息加工中的促进或干扰效应广泛存在。例如Starreveld等人(1996)的研究发现图-词刺激之间的语义相似性易引起语义干扰效应;Hughes等人(2005)证实了听觉偏差刺激的出现会影响系列回忆的成绩。而在Murray等人(2004)的研究中发现跨通道信号能增强事件记忆和知觉学习,对物体的视觉再认能从多感觉的编码中提取更多信息。那么这些通道间的促进或干扰效应是否也存在于数量空间表征这一过程中?
以往关于SNARC的研究多是以视觉方式呈现刺激,较少关注听觉通道的研究,且更少关注到跨通道呈现数量刺激情况下数量空间表征的研究。大量研究发现,数字空间表征具有受情境影响的特点,如依赖于数字的相对大小,而非绝对大小(Dehaene,Bossini,& Giraux,1993;Fias,Brysbaert,Geypens,& Ydewalle,1996),再如即便是相同或相似的数字序列,也会因为个体使用不同的空间参考框架来有意的匹配数字和空间而导致唤醒不同方向的SNARC效应(Viarouge,Hubbard,& Dehaene,2014;Vuilleumier,Ortigue,& Brugger,2004)。所以越来越多的研究发现SNARC效应具有灵活性、受情境影响的特点,可能是一种策略性的反应(Fischer,2006)。跨通道下同时呈现数量信息的研究将对SNARC效应的情境反应性特点进行进一步探索,并探索SNARC效应是否存在不同通道间的相互影响,如果存在,会是促进还是干扰效应,这是本研究想要考察的另一个重点。
本研究从跨通道的角度入手,将对跨通道下数量空间表征的特点进行探讨,更直观地比较单通道和跨通道下数量空间表征的差异。在实验一中,进行视、听两个通道的单通道基线任务,验证先前研究中在视、听两个通道下呈现数字信息,都可进行数量空间表征的结论,同时考察在视觉刺激、听觉刺激下进行数量空间表征是否表现出差异。在实验二中,视、听两通道刺激同时呈现,考察通道叠加时数量空间表征的特点以及视、听两通道在进行数量空间表征过程中的相互影响。在研究中,跨视听通道数字信息将同时呈现,其中一个通道的刺激作为提示信息,另一个通道的刺激作为主要考察通道,即分别考察视觉启动下听觉通道数量空间表征的情况和听觉启动下视觉通道数量空间表征的情况。并且启动通道的提示信息(非反应)分为与主通道(需要反应)内数量大小信息一致、不一致以及中性三种条件。通过比较SNARC效应值在两个通道分别启动时不一致条件下的大小,或比较在某个通道启动时三种提示条件下的大小等方式,考察跨通道间一致或不一致的提示信息是否会对主通道的SNARC效应造成影响、以及如何影响,产生促进还是干扰效应。
2 实验一 视觉与听觉通道中的SNARC效应 2.1 被试某校参加实验的研究生33名,男生17名,女生16名,均为健康成人,右利手,矫正视力正常,听力正常。被试的平均年龄为23.97±1.42岁。
2.2 材料和仪器视觉通道内,刺激为白色48号Arial字体呈现的阿拉伯数字1到9(除了5),注视点为“+”,字体颜色、大小与数字相同,注视点与数字均呈现在屏幕中央,屏幕背景为黑色;听觉通道内,刺激为女声汉语普通话读出的听觉数字1到9(除了5),通过内置式耳机呈现,音量控制在中等强度,声音刺激的音频格式为PCM,比特率为705kbps,采样速率为22.50kH,音频采样大小为16位;相同数字不连续出现。实验在保持日光灯照明的室内进行,实验仪器采用14英寸笔记本电脑,分辨率1280×800像素,刷新频率60Hz。
2.3 实验设计实验包含两个部分:视觉任务部分和听觉任务部分。实验为单因素被试内设计,自变量为刺激呈现通道(视觉通道、听觉通道),因变量为SNARC效应值(即回归斜率值)。
2.4 实验程序本研究依据Dehaene等人(1990)的数字大小判断任务,要求被试对数字1到9(除了5) 与数字5的大小比较进行判断,通过按键进行反应。在视觉任务部分中,被试对看到的数字进行反应,在听觉任务部分,被试对听到的数字进行反应。实验开始后,首先出现注视点“+”,500ms之后呈现刺激,被试需要又快又准确地做进行判断并反应。视觉通道部分中刺激在被试做出反应后消失,听觉部分中,刺激呈现时长为每个数字音频长度,平均为473.13ms。被试做出反应之后出现空屏1000ms,接着进入下一试次。每个数字在听觉条件和视觉条件下都对左右手反应进行平衡,即一半的试次左手对大数(即大于5的数字)反应、右手对小数(即小于5的数字)反应,另一半试次反之;同时,视觉任务部分与听觉任务部分的顺序也在被试间进行平衡。即实验1共分为4个block,分别为视觉任务部分下左手对小数反应、右手对大数反应的block和右手对小数反应、左手对大数反应的block,以及两个相应的听觉任务部分。每个block中每个数字随机呈现6次,即每个block有48个trial,整个实验四个block大概持续10分钟,block间隙时被试可以根据自己的状态适当休息。
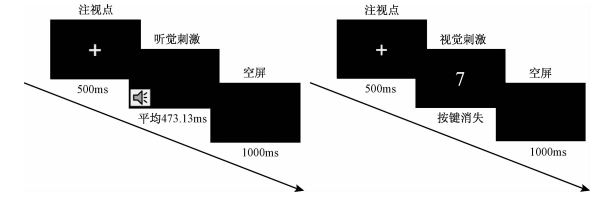
|
| 图 1 听觉部分(左图)和视觉部分(右图)一轮试次示意图 |
在分析SNARC效应时,首先分通道进行8(数字1到9(除了5))×2(左手、右手)的重复测量方差分析,计算是否出现SNARC效应及其特点;然后利用线性回归,以数字为自变量,以右手减去左手的反应时之差为因变量,计算不同条件下SNARC效应大小;最后比较不同条件下SNARC效应是否存在差异。
2.5.1 视觉通道下的SNARC效应对视觉通道任务中被试的错误率与正确反应时进行统计分析。删除错误率大于50%的被试1名(3.0%),同时剔除反应时在三个标准差以外的数据。删除后,被试的错误率范围为0%~11%,平均错误率为3.5%,正确反应的平均反应时为575.12±93.56ms。对正确率与反应时进行皮尔逊相关分析,发现两者不存在显著相关,r=0.008,p > 0.05,即不存在反应时与错误率的代偿。
在视觉通道下,32名被试在不同条件下的平均反应时数据见图 2。
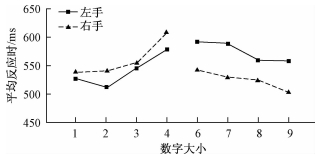
|
| 图 2 视觉通道下数字加工的反应时 |
进行8×2重复测量方差分析,结果发现,数字的主效应显著,F(7, 217)=9.73,p < 0.001,ηp2=0.24。反应手的主效应显著,F(1, 31)=7.42,p < 0.05,ηp2=0.19,被试左手的反应时显著长于右手的反应时。
数字与反应手的交互效应显著,F(7, 217)=4.30,p < 0.001,ηp2=0.12。进一步进行简单效应检验发现,被试对数字1、2、3进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字4进行反应时,左手的反应时显著快于右手(p < 0.05),对数字6、7、8、9进行反应时,右手显著快于左手(ps < 0.05),说明视觉通道下出现SNARC效应。
2.5.2 听觉通道下的SNARC效应听觉通道任务中,剔除反应时在三个标准差以外的数据。删除后,被试的错误率范围为0%~10%,平均错误率为3.3%,正确反应的平均反应时为722.35±127.59ms。对正确率与反应时进行皮尔逊相关分析,发现两者不存在显著相关,r=-0.03,p > 0.05,说明不存在反应时与错误率的代偿。
在听觉通道下,33名被试在不同条件下的平均反应时数据见图 3。
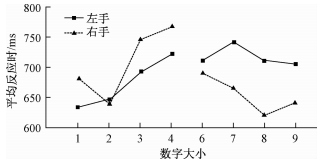
|
| 图 3 听觉通道下数字加工的反应时 |
进行8×2重复测量方差分析,结果发现,数字的主效应显著,F(7, 224)=11.68,p < 0.001,ηp2=0.27。反应手的主效应不显著,F(1, 32)=2.28,p > 0.05,ηp2=0.07,被试左右手的反应时没有显著差异。
数字与反应手的交互效应显著,F(7, 224)=5.11,p < 0.001,ηp2=0.14。进一步进行简单效应检验发现,被试对数字1、2、4、6进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字3进行反应时,左手的反应时显著快于右手(p < 0.05),对数字7、8、9进行反应时,右手显著快于左手(ps < 0.05),说明听觉通道下出现SNARC效应。
2.5.3 视听觉通道下SNARC效应的比较为了进一步考察并比较视觉与听觉通道下SNARC效应的差异。以数字为作为自变量,右手减去左手的反应时之差为因变量,进行线性回归分析(见图 4)。
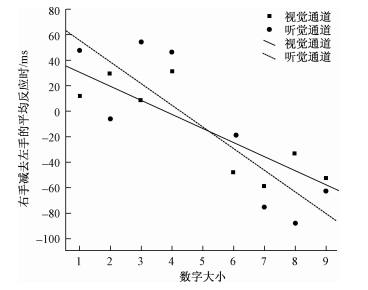
|
| 图 4 视觉与听觉通道下的SNARC效应比较 |
对于视觉通道,SNARC效应显著,B=-11.08,SE=2.34,β=-0.29,p < 0.001。听觉通道SNARC效应也显著,B=-16.97,SE=3.35,β=-0.30,p < 0.001。这个结果和方差分析的结果是基本一致的,即视觉和听觉通道下呈现刺激都出现了显著的SNARC效应。
两个回归系数没有显著差异,t (30)=1.52,p > 0.05,说明视觉与听觉通道的SNARC效应大小没有显著差异。
3 实验二 跨通道提示信息对SNARC效应的影响 3.1 被试参加实验一的被试33名。实验时,被试参加实验一和实验二的先后顺序在被试间进行平衡。
3.2 材料和仪器实验材料与实验一相似,增加了听觉与视觉的无关中性刺激。分别为:无意义音节“bi”,和无关符号,如“△”、“□”、“○”等。
3.3 实验设计实验分为视觉通道启动部分和听觉通道启动部分。实验为2(视觉通道启动、听觉通道启动)×3(一致情境、不一致情境、中性情境)被试内设计,因变量为个体SNARC效应值(即回归斜率值)。
3.4 实验程序仍采用大小比较任务,但实验刺激视听双通道同时呈现。在听觉反应通道部分中,要求被试在对视觉刺激保持注意的情况下,对听觉通道内呈现的数字进行反应;在视觉反应通道中,要求被试在对听觉刺激保持注意的情况下,对视觉通道的数字进行反应。两个通道刺激同时出现,视觉刺激在做出反应后消失,听觉刺激平均时长473.13ms,反应后出现空屏1000ms,然后进行下一试次。在实验中,要求被试在实验期间不能闭眼或摘掉耳机,需对两个通道的刺激保持注意。两个通道的刺激被设置成三个情境:数值大小的方向一致情境、方向不一致情境和中性情境:方向一致时,视听通道内呈现的两个数字与5相比结果相同,即都大于5或都小于5;方向不一致时结果相反,即启动通道的数字大于5,主通道数字小于5(或相反);中性条件时,启动通道内的刺激为无关符号或无意义音节,主通道仍为需要判断的数字。其中方向一致和方向不一致情境随机呈现,中性条件在独立的block中单独完成。与实验1相同,每个情况下均在被试内平衡左右手反应,被试间平衡视听反应通道。即实验2共分为8个block,分别为听觉通道启动-视觉反应通道条件下,左手对小数反应、右手对大数反应的block和右手对小数反应、左手对大数反应的block,视觉通道启动-听觉反应通道条件下相应的两个block,如图 5所示,以及四个中性条件的block:听觉部分下的左手小数右手大数block、右手小数左手大数block及视觉部分下的左手小数右手大数block、右手小数左手大数block,如图 6所示。在前4个block中,每个数字在方向一致和方向不一致情境下均随机呈现6次,即每个block中每个数字呈现12次,共96个trial;在中性条件的每个block中,每个数字随机呈现6次,共48个trial。整个实验大概持续30分钟,block间隙时被试可以根据自己的状态适当休息。
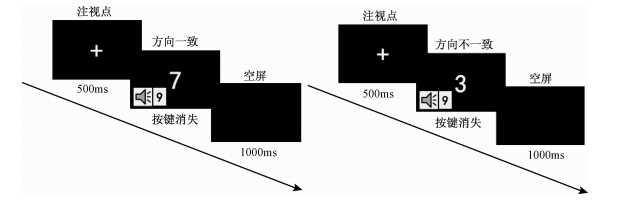
|
| 图 5 两通道方向一致(左图)和方向不一致(右图)一轮试次示意图 |
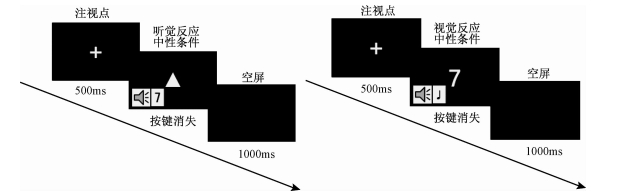
|
| 图 6 中性条件下听觉反应(左图)和视觉反应(右图)一轮试次示意图 |
与实验1相似,在分析SNARC效应时,先在每种条件下进行8(数字1到9(除了5))×2(左手、右手)的重复测量方差分析,计算不同实验条件下是否出现SNARC效应及其特点;然后利用线性回归,
以数字为自变量,以右手减去左手的反应时之差为因变量,计算不同条件下的SNARC效应大小;最后比较不同条件下的SNARC效应是否存在差异。
3.5.1 不同听觉提示信息对视觉反应通道SNARC效应的影响对视觉反应通道任务中被试的错误率与正确反应时进行统计分析。在视觉与听觉一致条件下,删除错误率大于50%的被试3名(9.1%),同时剔除反应时在三个标准差以外的数据。剩下30名被试的错误率范围为0%~11%,平均错误率为3.1%,正确反应的平均反应时为526.48±87.93ms。正确率与反应时不存在显著相关,r=-0.07,p > 0.05。在视觉与听觉不一致条件下,删除错误率大于50%的被试3名(9.1%),同时剔除反应时在三个标准差以外的数据。剩下30名被试的错误率范围为0%~17%,平均错误率为4.1%,正确反应的平均反应时为533.29±97.41ms。正确率与反应时不存在显著相关,r=-0.14,p > 0.05。在中性情况下,删除错误率大于50%的被试2名(6.0%),同时剔除反应时在三个标准差以外的数据。剩下31名被试的错误率范围为0%~12%,平均错误率为3.9%,正确反应的平均反应时为509.77±86.90ms。正确率与反应时不存在显著相关,r=0.29,p > 0.05。
被试在不同条件下的平均反应时数据见图 7。
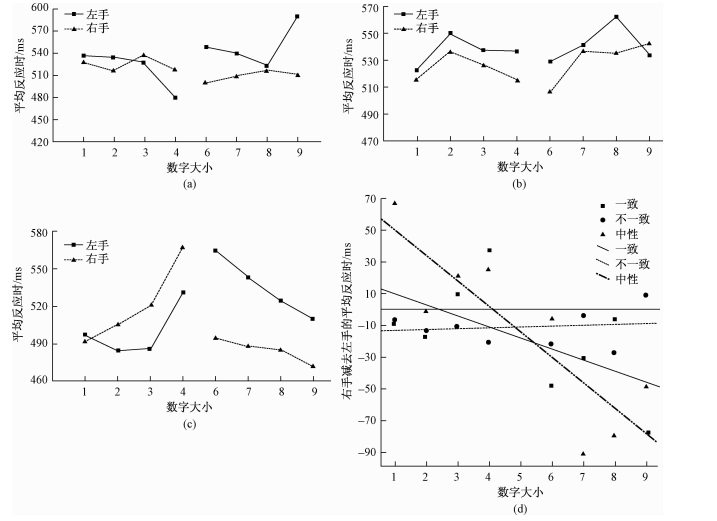
|
| 图 7 不同听觉提示信息对视觉SNARC效应的影响 注:a为听觉提示信息与视觉信息一致条件,b为听觉提示信息与视觉信息不一致条件,c为听觉提示信息为中性条件,d为三种条件下SNARC效应大小的比较 |
在听觉提示信息与视觉信息一致情况下,进行8×2重复测量方差分析(见图 7a),结果发现,数字的主效应显著,F(7, 203)=4.26,p < 0.001,ηp2=0.13;反应手的主效应显著,F(1, 29)=8.99,p < 0.01,ηp2=0.24,被试左手的反应时显著长于右手的反应时;数字与反应手的交互效应显著,F(7, 203)=4.65,p < 0.001,ηp2=0.14。简单效应检验发现,被试对数字1、2、3、7、8进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字4进行反应时,左手的反应时显著快于右手(p < 0.05),对数字6、9进行反应时,右手显著快于左手(ps < 0.05)。
在听觉提示信息与视觉信息不一致情况下,进行8×2重复测量方差分析(见图 7b),结果发现,数字的主效应显著,F(7, 203)=2.67,p < 0.05,ηp2=0.08;反应手的主效应显著,F(1, 29)=6.84,p < 0.05,ηp2=0.19,被试左手的反应时显著长于右手的反应时;数字与反应手的交互效应不显著,F(7, 203)=0.43,p > 0.05,ηp2=0.02。
当听觉提示信息为中性刺激时,进行8×2重复测量方差分析(见图 7c),结果发现,数字的主效应显著,F(7, 210)=0.90,p < 0.001,ηp2=0.25;反应手的主效应显著,F(1, 30)=9.81,p < 0.01,ηp2=0.25,被试左手的反应时显著长于右手的反应时;数字与反应手的交互效应显著,F(7, 210)=8.22,p < 0.001,ηp2=0.22。简单效应检验发现,被试对数字1、2进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字3、4进行反应时,左手的反应时显著快于右手(ps < 0.05),对数字6、7、8、9进行反应时,右手显著快于左手(ps < 0.05)。
为了进一步探讨不同听觉提示信息对视觉反应通道SNARC效应大小影响的差异,以数字为作为自变量,右手减去左手的反应时之差为因变量,进行线性回归分析(见图 7d)。
当听觉提示信息与视觉信息数量大小方向一致时,SNARC效应显著,B=-6.95,SE=2.21,β=-0.20,p < 0.01。当听觉提示信息与视觉信息不一致时,SNARC效应不显著,B=0.58,SE=2.20,β=0.02,p > 0.05。当听觉提示信息为中性刺激时,SNARC效应显著,B=-10.02,SE=1.96,β=-0.31,p < 0.001。
比较提示信息为中性与无任何提示信息时的SNARC效应,结果发现,两个回归系数没有显著差异,t (30)=0.40,p > 0.05,说明听觉通道的无关刺激对视觉的SNARC效应没有显著影响。比较提示信息与视觉信息一致条件与提示信息为中性条件下的SNARC效应大小,结果发现,两个回归系数也没有显著差异,t (30)=1.12,p > 0.05,说明听觉通道呈现一致信息或无关信息,视觉的SNARC效应大小没有显著差异。但当听觉呈现不一致提示信息时的SNARC效应大小消失,回归系数显著低于呈现一致信息(t (30)=2.23,p < 0.05) 和中性刺激时(t (30)=3.52,p < 0.001) 的系数。说明不一致的听觉提示信息对视觉的SNARC效应大小造成干扰。
3.5.2 不同视觉提示信息对听觉SNARC效应的影响对听觉通道任务中被试的错误率与正确反应时进行统计分析。在视觉与听觉一致条件下,删除错误率大于50%的被试1名(3.0%),同时剔除反应时在三个标准差以外的数据。剩下32名被试的错误率范围为0%~11%,平均错误率为3.5%,正确反应的平均反应时为684.37±106.95ms。正确率与反应时不存在显著相关,r=0。在视觉与听觉不一致条件下,删除错误率大于50%的被试1名(3.0%),同时剔除反应时在三个标准差以外的数据。剩下32名被试的错误率范围为2%~23%,平均错误率为6.9%,正确反应的平均反应时为702.54±100.06ms。正确率与反应时不存在显著相关,r=-0.05,p > 0.05。在中性情况下,删除错误率大于50%的被试3名(9.1%),同时剔除反应时在三个标准差以外的数据。剩下30名被试的错误率范围为0%~18%,平均错误率为5.1%,正确反应的平均反应时为657.02±90.06ms。正确率与反应时不存在显著相关,r=-0.06,p > 0.05。
被试在不同条件下的平均反应时数据见图 8。
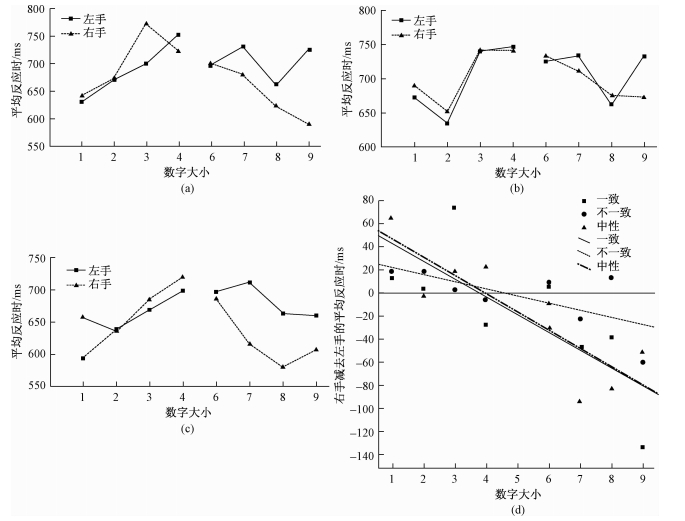
|
| 图 8 不同视觉提示信息对听觉SNARC效应的影响 注:a为视觉提示信息与听觉信息一致条件,b为视觉提示信息与听觉信息不一致条件,c为视觉提示信息为中性条件,d为三种条件下SNARC效应大小的比较 |
在视觉提示信息与听觉信息一致情况下,进行8×2重复测量方差分析(见图 8a),结果发现,数字的主效应显著,F(7, 217)=18.31,p < 0.001,ηp2=0.37;反应手的主效应显著,F(1, 31)=6.65,p < 0.05,ηp2=0.18,被试左手的反应时显著长于右手的反应时;数字与反应手的交互效应显著,F(7, 217)=5.99,p < 0.001,ηp2=0.16。进行简单效应检验发现,被试对数字1、2、4、6、8进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字3进行反应时,左手的反应时显著快于右手(p < 0.05),对数字7、9进行反应时,右手显著快于左手(ps < 0.05)。
在视觉提示信息与听觉信息不一致情况下,进行8×2重复测量方差分析(见图 8b),结果发现,数字的主效应显著,F(7, 217)=13.98,p < 0.05,ηp2=0.31;反应手的主效应不显著,F(1, 31)=0.13,p > 0.05,ηp2=0.004;数字与反应手的交互效应不显著,F(7, 217)=1.42,p > 0.05,ηp2=0.04。
当视觉提示信息为中性刺激时,进行8×2重复测量方差分析(见图 8c),结果发现,数字的主效应显著,F(7, 203)=14.46,p < 0.001,ηp2=0.33;反应手的主效应显著,F(1, 29)=9.54,p < 0.01,ηp2=0.25,被试左手的反应时显著长于右手的反应时;数字与反应手的交互效应显著,F(7, 203)=7.48,p < 0.001,ηp2=0.21。简单效应检验发现,被试对数字2、3、4、6进行反应时,左右手的反应时没有显著差异(ps > 0.05),但对数字1进行反应时,左手的反应时显著快于右手(p < 0.05),对数字7、8、9进行反应时,右手显著快于左手(ps < 0.05)。
为了进一步探讨不同视觉提示信息对听觉SNARC效应大小影响的差异,以数字为作为自变量,右手减去左手的反应时之差为因变量,进行线性回归分析(见图 8d)。
当视觉提示信息与听觉信息一致时,SNARC效应显著,B=-15.37,SE=3.19,β=-0.29,p < 0.001。当视觉提示信息与听觉信息不一致时,SNARC效应显著,B=-6.11,SE=2.90,β=-0.13,p < 0.05。当视觉提示信息为中性刺激时,SNARC效应显著,B=-15.99,SE=2.57,β=-0.37,p < 0.001。
比较视觉提示信息为中性与无任何提示信息时的听觉SNARC效应,结果发现,两个回归系数没有显著差异,t (30)=0.24,p > 0.05,说明视觉通道的无关刺激对听觉的SNARC效应没有显著影响。比较视觉提示信息与听觉信息一致条件与提示信息为中性条件下的SNARC效应大小,结果发现,两个回归系数也没有显著差异,t (30)=0.13,p > 0.05,说明视觉通道呈现一致信息或无关信息,听觉的SNARC效应大小没有显著差异。但当视觉呈现不一致提示信息时的SNARC效应大小显著地低于呈现一致信息(t (30)=2.69,p < 0.01) 或中性刺激时(t (30)=2.78,p < 0.01) 的SNARC效应大小。说明不一致的视觉提示信息对听觉的SNARC效应大小造成干扰。
4 讨论本研究利用两个实验首先比较视觉和听觉通道下的SNARC效应是否存在差异,并进一步探究跨通道的一致或不一致提示信息是否会对主通道的SNARC效应造成影响。结果显示,单通道反应下,视觉通道和听觉通道均存在SNARC效应,但两者的SNARC效应大小没有显著差异。而在跨通道任务下,结果发现,启动通道的不同信息对主通道的SNARC效应的影响存在差异。无论启动通道是视觉还是听觉通道,都表现出当启动通道的数量大小信息与主通道的信息大小一致或无关时,主通道的SNARC效应没有显著变化;但当启动通道的数量大小信息与主通道不一致时,主通道的SNARC效应受到显著影响,表现为降低或消失。另外,在无关刺激情境下,无论在视觉反应通道还是在听觉反应通道任务中,另一个通道的无关刺激对反应通道SNARC效应的影响与单通道基线任务相比,均没有显著差异。这个结果进一步证明了SNARC效应受情境影响的特点,并第一次发现空间数量表征受到跨通道信息的影响,且只有跨通道的数量信息才会影响主通道的数量空间表征,具有干扰的特异性。
在以往研究中,SNARC效应已被证明广泛存在于各种形式及各种呈现方式的数字信息中(金桂春,王强强,王有智,吴彦文,2016),即数量的空间表征可以发生在视觉通道和听觉通道。在本研究实验一中,进行视、听两通道的单通道基线任务,并在视觉、听觉通道下都发现了显著的SNARC效应的发生,验证了先前研究结果,进一步证明了SNARC效应广泛的存在于不同的通道中。
实验二的结果表明方向不一致的听觉和视觉提示信息对另一通道的SNARC效应大小造成干扰,且这一干扰是由于非反应通道的提示数字信息造成的。在提示信息与反应通道内的刺激方向一致时,并没有出现促进作用,反而出现了一定程度的干扰,令SNARC效应呈现出减弱的趋势,但是差异并未达到显著水平。出现这一结果的原因可能是由于两个通道的信息同时呈现时,被试同时加工了两个通道内的数字信息,分散了对反应通道的注意力,因此,对反应通道内无意识的SNARC过程造成干扰,致其SNARC效应有所降低。这在不一致的提示信息条件下更为明显。当提示信息不一致时,两个通道内的结果产生冲突,被试需要有意识地选择正确的结果,因而对无意识过程中的SNARC效应造成很大干扰。当呈现一致的提示信息时,两个通道内比较的结果相同,被试能尽快做出反应,因此,对SNARC效应的干扰较不一致条件下小。对SNARC效应干扰最小的是无关提示信息条件。在所有任务中,被试都只需要对数字进行反应,因此,当呈现无关信息时,被试可能并没有对这些刺激进行加工,而将认知资源集中在反应通道的数字上,因此,对SNARC效应几乎没有干扰。
这样的结果类似于以往关于工作记忆的研究结果。近年来,大量研究表明SNARC效应具有很强的情境依赖性(Fischer,Mills,Shaki,2010),而工作记忆作为一种对信息进行短暂加工和储存的记忆系统,在很多认知活动中起重要作用。目前已有研究表明工作记忆也影响着SNARC效应的发生(Lindemann,Abolafia,Pratt,& Bekkering,2008)。在已有的关于工作记忆的研究中,Kim、Kim和Chung(2005)发现当工作记忆的内容和目标信息的属性(如言语工作记忆对应言语目标信息)一致时,工作记忆负荷的增加会导致干扰效应的增强。而胡耿丹、金志成(2009)发现,当工作记忆的内容和干扰的属性一致时,会减小干扰效应的存在;当工作记忆和目标信息竞争资源时,会导致对干扰加工的增加。因此在本研究中,可能是由于当出现不一致信息时,不同通道间的两个数字间的距离变大,工作记忆的负荷增加,干扰效应增强;而当出现一致信息时,工作记忆内容与干扰的属性一致,减小干扰效应。
在实验二的研究中我们还发现,当在视觉通道启动的情境下,听觉信息与视觉信息方向不一致时,SNARC效应不显著,且显著低于一致和中性条件;而在听觉通道启动的情境下,两通道间信息方向不一致时,SNARC效应显著,且显著低于一致和中性条件。这个结果可能暗示,在进行跨通道数量空间表征时,听觉通道的信息对视觉通道的影响大于视觉通道的信息对听觉通道的影响。以往研究中,Szucs等人(2004)在SNARC效应的ERP研究中发现,听觉刺激和视觉刺激引起的SNARC效应在N100和P400差异显著,听觉刺激引发更强的N100。这种在ERP上表现出来的差异也许是造成跨通道数量空间表征时听觉通道对视觉通道的影响更大的原因。所以后续研究,我们可能会从ERP的角度入手考察这一影响和差异。
5 结论本研究得到以下结论:(1) 视、听两通道下均能进行数量空间表征,都表现出显著的SNARC效应;(2) 当听觉通道呈现与视觉反应通道方向一致或中性的提示信息时,视觉反应通道的SNARC效应大小没有显著差异,但当方向不一致时,视觉反应通道的SNARC效应消失;当视觉通道呈现与听觉方向一致或中性的提示信息时,听觉反应通道的SNARC效应大小没有显著差异;当方向不一致时,听觉反应通道的SNARC效应显著降低;(3) 在进行跨通道数量空间表征时,听觉通道的信息对视觉通道的影响大于视觉通道的信息对听觉通道的影响。
| Dehaene S., Bossini S., & Giraux P.(1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology:General, 122(3), 371-396. DOI: 10.1037/0096-3445.122.3.371. |
| Dehaene S., Dupoux E., & Mehler J.(1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. Journal of Experimental Psychology:Human Perception and Performance, 16(3), 626-641. DOI: 10.1037/0096-1523.16.3.626. |
| Durk T., Daniel S., Salvador S., & Marty G. W.(2010). The multifaceted interplay between attention and multisensory integration. Trends in Cognitive Sciences, 14(9), 400-410. DOI: 10.1016/j.tics.2010.06.008. |
| Fias W., Brysbaert M., Geypens F., & d'Ydewalle G.(1996). The importance of magnitude information in numerical processing:Evidence from the SNARC effect. Mathematical Cognition, 2(1), 95-110. DOI: 10.1080/135467996387552. |
| Fischer M. H.(2006). The future for SNARC could be stark…. Cortex, 42(8), 1066-1068. DOI: 10.1016/S0010-9452(08)70218-1. |
| Fischer M.H., Mills R.A., & Shaki S.(2010). How to cook a SNARC:Number placement in text rapidly changes spatial-numerical associations. Brain and Cognition, 72(3), 333-336. DOI: 10.1016/j.bandc.2009.10.010. |
| Fischer M. H., Riello M., Giordano B. L., & Rusconi E.(2013). Singing numbers … in cognitive space. Topics in Cognitive Science, 5(2), 354-366. DOI: 10.1111/tops.12017. |
| Golob EJ, Lewald J, Jungilligens J, & Getzmann S.(2016). Interaction of number magnitude and auditory localization. Perception, 45(1-2), 165-179. DOI: 10.1177/0301006615599906. |
| Hughes R. W., Vachon F., & Jones D. M.(2005). Auditory attentional capture during serial recall:Violations at encoding of an algorithm-based neural model. Journal of Experimental Psychology:Learning, Memory, and Cognition, 31(4), 736-749. DOI: 10.1037/0278-7393.31.4.736. |
| Kim S. Y., Kim M. S., & Chun M. M.(2005). Concurrent working memory load can reduce distraction. Proceedings of the National Academy of Sciences, 102(45), 16524-16529. DOI: 10.1073/pnas.0505454102. |
| Lidji P., Kolinsky R., Lochy A., Karnas D., & Morais J.(2007). Spatial associations for musical stimuli:A piano in the head?. Journal of Experimental Psychology:Human Perception and Performance, 33(5), 1189-1207. DOI: 10.1037/0096-1523.33.5.1189. |
| Lindemann O., Abolafia J.M., Pratt J., & Bekkering H.(2008). Coding strategies in number space:Memory requirements influence spatial-numerical associations. Quarterly Journal of Experimental Psychology, 61(4), 515-524. DOI: 10.1080/17470210701728677. |
| Murray M. M., Michel C. M., Grave de Peralta R., Ortigue S., Brunet D., Gonzalez A. S., & Schnider A.(2004). Rapid discrimination of visual and multisensory memories revealed by electrical neuroimaging. NeuroImage, 21(1), 125-135. DOI: 10.1016/j.neuroimage.2003.09.035. |
| Nuerk H. C., Wood G., & Willmes K.(2005). The universal SNARC effect:The association between number magnitude and space is amodal.. Experimental Psychology, 52(3), 187-194. DOI: 10.1027/1618-3169.52.3.187. |
| Pfister R., Schroeder P. A., & Kunde W.(2013). SNARC struggles:Instant control over spatial-numerical associations. Journal of Experimental Psychology:Learning, Memory, and Cognition, 39(6), 1953-1958. DOI: 10.1037/a0032991. |
| Previtali P., de Hevia M. D., & Girelli L.(2010). Placing order in space:the SNARC effect in serial learning. Experimental Brain Research, 201(3), 599-605. DOI: 10.1007/s00221-009-2063-3. |
| Shaki S., Fischer M. H., & G bel S. M.(2012). Direction counts:A comparative study of spatially directional counting biases in cultures with different reading directions. Journal of Experimental Child Psychology, 112(2), 275-281. DOI: 10.1016/j.jecp.2011.12.005. |
| Starreveld P. A., & La Heij W.(1996). Time-course analysis of semantic and orthographic context effects in picture naming. Journal of Experimental Psychology:Learning, Memory, and Cognition, 22(4), 896-918. DOI: 10.1037/0278-7393.22.4.896. |
| Stein B.E., & Stanford T. R.(2008). Mutisensory integration, current issues from the perspective of the single neuron. Nature Reviews Neuroscience., 9(4), 255-266. DOI: 10.1038/nrn2331. |
| Szucs D., & Csepe V.(2004). Access to numerical information is dependent on the modality of stimulus presentation in mental addition:A combined ERP and behavioral study. Brain research. Cognitive Brain Research, 19(1), 10-27. DOI: 10.1016/j.cogbrainres.2003.11.002. |
| Viarouge A., Hubbard E. M., & Dehaene S.(2014). The organization of spatial reference frames involved in the SNARC effect. The Quarterly Journal of Experimental Psychology, 67(8), 1484-1499. DOI: 10.1080/17470218.2014.897358. |
| Viarouge A., Hubbard E. M., & McCandliss B. D.(2014). The cognitive mechanisms of the SNARC effect:An individual differences approach. PLoS One, 9(4), e95756. DOI: 10.1371/journal.pone.0095756. |
| Vuilleumier P., Ortigue S., & Brugger P.(2004). The number space and neglect. Cortex, 40(2), 399-410. DOI: 10.1016/S0010-9452(08)70134-5. |
| Wood G., Willmes K., Nuerk H.C., & Fischer M.H.(2008). On the cognitive link between space and number:A meta-analysis of the SNARC effect. Psychology Science Quarterly, 50(4), 489-525. |
| 陈英和. (2015). 儿童数量表征与数概念的发展特点及机制. 心理发展与教育, 31(1), 21-28. |
| 陈英和, 赖颖慧. (2013). 儿童非符号数量表征的特点及作用探析. 北京师范大学学报(社会科学版), 1(1), 33-41. |
| 胡耿丹, 金志成. (2009). 工作记忆负载对位置干扰子激活加工和抑制加工的影响. 心理学报, 41(4), 292-304. |
| 金桂春, 王强强, 王有智, 吴彦文. (2016). 数字SNARC效应大小和顺序信息的分离. 心理与行为研究, 14(2), 228-233. |
| 孔风, 赵晶晶, 游旭群, 张宇. (2012). 听觉通道下负数的低水平加工引起注意的SNARC效应. 心理与行为研究, 10(1), 12-17. |
| 潘运, 白学军, 沈德立, 赵守盈. (2012). 内源性注意和外源性注意对中小学生SNARC效应的影响. 心理发展与教育, 28(6), 561-568. |
 2017, Vol. 33
2017, Vol. 33


