国家教育部主管、北京师范大学主办。
文章信息
- 高婷, 刘儒德, 刘颖, 庄鸿娟 .2016.
- GAO Ting, LIU Rude, LIU Ying, ZHUANG Hongjuan .2016.
- 小学生分数比较中的加工模式:基于反应时和口语报告的研究
- The Processing of Fractions Comparison Task in Elementary Students: Reaction Time and Trial-by-Trial Strategy Reports as Evidences
- 心理发展与教育, 32(4): 463-470
- Psychological Development and Education, 32(4): 463-470.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2016.04.10
分数比较是指让学生对两个分数的大小进行判断,所比较的两个分数往往涉及同分子分数对、同分母分数对以及异分子异分母分数对三种类型。对于个体在完成分数比较任务中的加工模式,目前存在三种不同的研究结论。一是成分加工模式(Bonato,Fabbri,Umiltà,& Zorzi,2007; Liu,Xin,Lin,& Thompson,2013; Meert,Grégoire,& Noël,2009; Zhang,Fang,Gabriel,& Szü,2014),即基于一种离散系统来表征分数,将分数的分子和分母分别加工,仅仅对分数成分进行加工就能完成任务;二是整体加工模式(Meert et al., 2009; Obersteiner,Van Dooren,Van Hoof,& Verschaffel,2013; Schneider & Siegler, 2010; Sprute & Temple, 2011),即基于分数实际数值的连续系统来表征分数,直接加工他们的实际数值来完成任务;三是混合加工模式(Faulkenberry & Pierce, 2011; Meert,Grégoire,& Noë,2010),即既有成分加工,又有整体加工。
上述相互矛盾的研究结论建立在这样一个研究范式的基础之上:以被试的反应时和正确率作为因变量,以所比较的分数对的数字距离和问题大小作为预测变量进行回归分析(Faulkenberry & Pierce, 2011; Meert et al., 2009,2010; Schneider & Siegler, 2010),然后根据回归分析结果中显著的预测变量来判定被试进行分数比较时的加工模式。数字距离包括两种:两个分数之间的实际数值距离(以下简称实值距离);两个分数的分子之间或分母之间距离(以下简称成分距离)。若是两分数之间的实值距离能显著预测反应时或者正确率,则为整体加工;若是两分数之间的成分距离能显著预测反应时或者正确率,则为成分加工,而且根据距离效应(Moyer & Landauer, 1967),反应时(和正确率)随着被比较的两个分子数或分母数的差距增大而减小(和增加)(Schneider & Siegler, 2010)。对于同分母分数对或同分子分数对,数字距离(实值距离与分子距离或分母距离)构成了所有的预测变量。但是,对于异分子异分母分数对,研究者们还采用另外一个预测变量—问题大小(Faulkenberry & Pierce, 2011)。根据问题大小效应,人在做数学运算时,解决数字较小的问题比数字较大问题速度更快、正确率更高(Ashcraft,1992)。如果被试采用成分加工模式,被试往往分别关注两个分数的分子或分母(而非每个分数的实际数值大小),因此两个分数的分子分母的数字大小就会影响被试的加工速度和准确率。研究者们采用两个分数的交叉乘积的均值作为问题大小的指标,如果这一预测变量显著,则说明被试的加工模式为成分加工模式(Faulkenberry & Pierce, 2011)。总结起来,在这一研究范式中,对于同分母或同分子分数对,两分数的实值距离是整体加工模式的预测指标;两分数的成分距离(分子距离或分母距离)是成分加工的预测指标。在此基础上,对于异分子异分母分数对,外加交叉乘积均值作为成分加工的预测指标。
然而,这种回归分析的研究范式存在一个内在的不足,即在不同类型的分数对中预测变量之间的相关程度存在差异,这种差异会影响回归分析结果。在上述方法中两个分数之间的实值距离、成分距离和问题大小的相关程度在不同类型、不同大小的分数对中是变化不定的,例如对于同分母分数,实值大小与分子大小成正比例函数,两个分数的实值距离会随着成分距离变大而按比例地变大;对于同分子分数,实值大小与分母大小成反比例函数,两个分数的实值距离随着成分距离变大而按非比例地变大;对于异分子异分母分数,实值大小与分子分母的关系是复杂的,两个分数的实值距离和成分距离之间的关系并不恒定。这意味着,根据回归分析的结果判定分数比较加工模式,其有效性和稳定性会极大受到所选用的分数对的材料的影响,因而值得质疑,这也可能是导致研究者们对分数比较加工模式做出相互矛盾的结论的一个重要原因。
近期的一些研究表明,被试对策略的选择可能直接反映了分数的加工模式(Faulkenberry & Pierce, 2011; Obersteiner et al., 2013; 辛自强,李丹,2013)。基于整体加工模式的策略,诸如标杆策略、化为小数策略等,从加工角度来看,被试考虑了分子和分母之间的关系,可能会激活分数整体值的表征(Obersteiner et al., 2013),例如,在以1/2为标杆的策略中,15/41小于13/24是因为15/41<1/2且13/24>1/2。该策略同时考虑了分子和分母之间的比例关系,激活了分数整体值的表征,符合整体加工模式的定义。基于成分加工模式的策略仅需关注分数成分的大小就可以完成任务,而无需加工分数的连续整体实值大小(Faulkenberry & Pierce, 2011)。例如,标准算术(standard algorithms),也叫通分,将分数转换为同分母再进行分子之间的比较;交叉相乘法(cross-multiplication),例如,a/b相比于c/d,通过比较a×d和c×b的大小来确定两个分数的大小;剩余策略,是分别用1减去两个分数后,再比较两个差值的分母大小。例如,3/4与6/7,分别用相减得到1/4与1/7,然后进行同分子分数的比较,只需比较两个分母。从加工角度来看,被试在使用上述策略时,仅考虑了分子或者分母之间的距离,并未考虑在同一分数下两者的关系,以一种离散的形式完成了分数的比较任务,符合成分加工模式的定义。分数对存在一定规律的情况下,如同分子或者同分母分数,被试可通过基于成分加工模式的策略来完成任务,而推广到分数对无规律的情况下,如异分子异分母,被试会因为很难生成基于成分加工模式的策略(Schneider & Siegler, 2010),或者说只比较分数的分子或者分母并不能一贯性地得到正确答案,转而利用整体策略去加工分数的真值(Meert et al., 2010)。对被试口语报告的策略进行记录和分析,可以更直观清晰地考查出被试在分数比较任务中所采用的加工模式。
本研究拟将采用口语报告的方式获取我国小学生在分数比较任务中的加工策略,作为其加工模式的直接证据,同时收集被试的反应时和正确率,通过前述的回归分析方法,采用两个分数的实值距离、成分距离和问题大小对反应时的预测的显著与否作为加工模式的间接证据,探查我国小学生在分数比较任务中的加工模式。在此基础上验证来自口语报告的直接证据与基于回归分析的间接证据的不一致性,以证实本研究对回归分析方法有效性的质疑。具体而言,根据直接证据,对被试实际采用整体加工策略的所有任务和实际采用成分加工策略的所有任务分别进行前述回归分析,如果实值距离显著预测所有整体加工任务的反应时,成分距离和问题大小能够显著预测所有成分加工任务的反应时,那么,回归分析的间接结果与口语报告的直接证据是一致的,否则,两者就是不一致的。
2 研究方法 2.1 被试选取北京和四川两所小学的六年级学生53名(男女各为20人和33人),平均年龄11.7岁,均为右利手,且口语表达清楚。由于对反应时的分析通常需要被试有较高的正确率,这就需要被试在电脑上进行分数比较时确实充分理解了分数概念(Liu et al., 2013),本研究的被试均通过了一次简单的有关分数理解的纸笔测试,以确认他们在后续的实验中具有分数的基本知识(Bonato et al., 2007)。
2.2 实验任务与研究设计为了完整地考察同一被试在三类分数比较中所采用的心理加工模式,所有被试均完成三类分数比较任务:8对同分子分数(x/a_x/b,如2/5_2/7)、8对同分母分数(a/x_b/x,如2/5_3/5)和16对异分子异分母分数(a/x_b/y,如3/7_5/8),共32个Trials。所有分数均为最简分数。
本研究拟将从三个方面做出分析。第一,直接证据分析。对口语报告的具体策略进行收集,并按照它们所属的加工模式进行归类,统计基于两种加工模式的策略的频次,本研究假设,如果基于整体加工的策略显著多于基于成分加工的策略,则为整体加工,反之为成分加工。第二,间接证据分析。从分数特征对反应时进行回归分析。因变量为被试完成分数比较任务的反应时,预测变量为分数对之间的实值距离、成分距离和问题大小,本研究假设,如果只有实值距离预测作用显著,表明被试对分数进行了整体加工;如果只有成分距离或者问题大小预测显著,则表明被试对分数进行了成分加工。第三,两种证据的对比分析。按照口语报告策略所属加工模式的类型,对两类策略所涵盖的trials的反应时做回归分析,本研究假设,如果在基于成分加工的策略下成分距离和问题大小预测作用显著,而且在基于整体加工的策略下实值距离预测作用显著,则两方面证据一致,反之不然。
2.3 程序本实验采用个体施测。指导语在电脑屏幕上呈现,被试准确理解指导语后按空格键进入下一环节。正式实验前有4个练习trials,在此期间被试可得到结果反馈,并且练习口语报告,确保被试理解实验要求后再开始正式实验。总测试时间为20分钟。
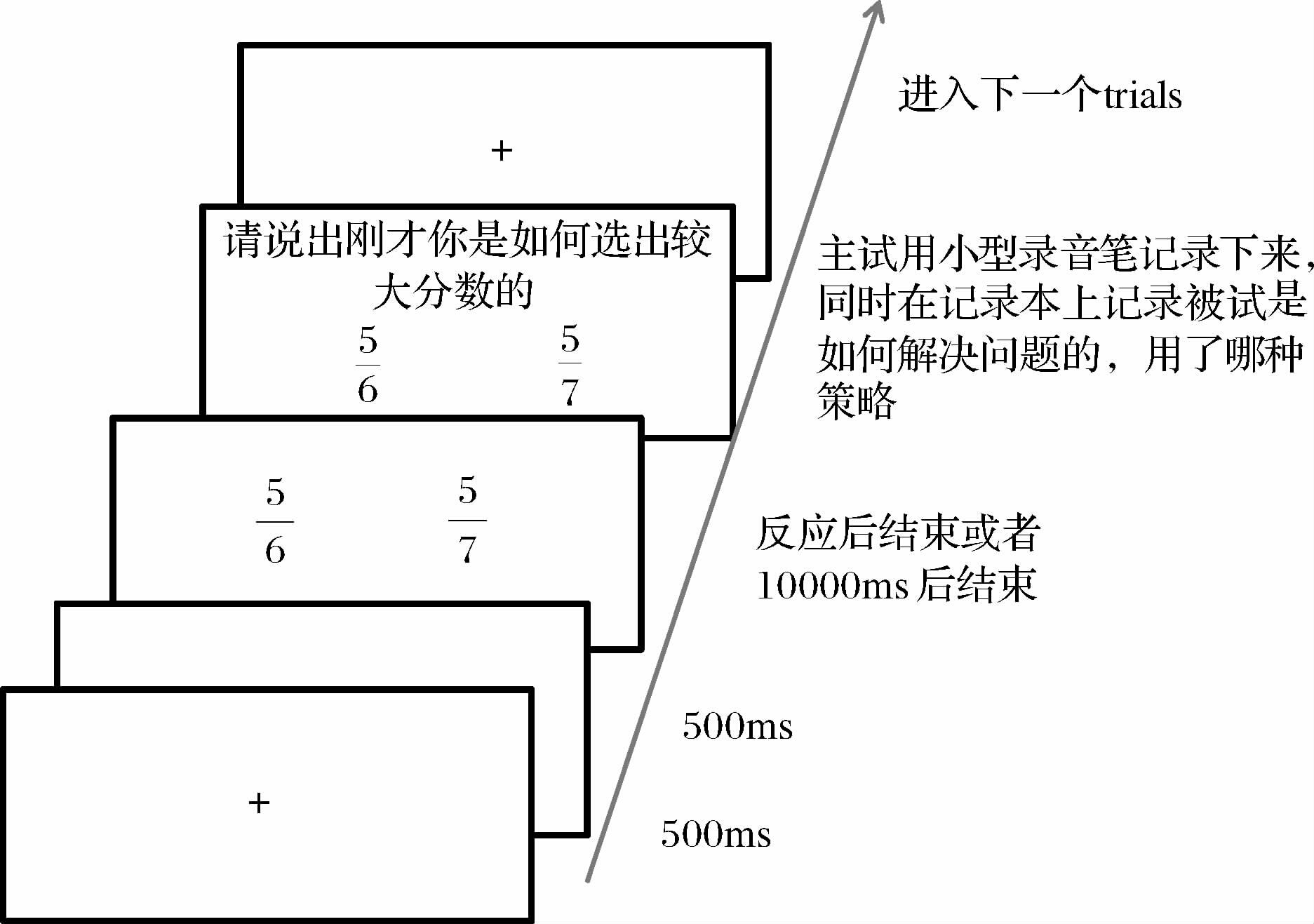
本实验的32个trials中的每一分数对仅呈现一次,对较大分数在屏幕上出现的左右位置进行平衡化处理(Faulkenberry & Pierce, 2011; Meert et al., 2009,2010)。分数以分子在上、分母在下,平行线分割的形式,黑色字体垂直呈现在白色背景的电脑屏幕上。每个分数大小为宽 11mm×长33mm。视距大约为60cm。实验开始后,在屏幕两侧会同时呈现两个分数,要求被试通过按键判断两个分数的大小,若数值较大的分数在左侧,按“←”键;若数值较大的分数在右侧,按“→”键。每个trials中,在电脑屏幕中央呈现注视点“+”,持续时间为500 ms;注视点消失后,是500 ms的空屏;接着分数对呈现在与注视点“+”相同的位置,直到被试做出按键反应或者10000 ms后自动消失;紧接着在屏幕中呈现一个句子“请说出刚才你是如何选出较大分数的”,句子下同时呈现刚才的分数对,待被试说出后比较方法后,进行下一个任务(图 1)。刺激任务的呈现和行为数据(反应时和正确率)的收集由E-prime1.1来实现。
|
| 图 1 实验程序示例 |
被试被要求在保证准确的前提下尽量快地反应,从刺激呈现到被试做出按键反应的时间记录为被试反应时。被试被要求清晰地描述所用方法的细节,主试在主试手册上记录下被试报告的策略,同时用录音笔录音。
2.4 统计分析使用SPSS18.0统计软件对数据进行分析。
在已有研究的基础上(Clarke & Roche, 2009; Faulkenberry & Pierce, 2011),根据本研究实际制定了分数比较任务策略的编码标准(表 1)。由一名主试当场对照策略编码表记录被试口语报告,另一名主试对现场录音进行策略评估和归类。编码前训练两名编码者在编码标准的认同度上的一致性比例达90%以上方可进行独立编码。
| 策略名称 | 界定 |
| 看分子/分母 | 分子相同,看分母;分母相同,看分子 |
| 通分 | 将分数化为同分母/同分子 |
| 交叉相乘 | 将两个分数的分子分母交叉相乘,比较乘积 |
| 剩余策略 | 比较1与分数之差,差值分母小者分数大 |
| 标杆策略 | 将两个分数分别与第三个数对比,通常是1或1/2 |
| 化为小数 | 先将分数转化为小数,再进行大小对比 |
剔除了反应时在三个标准差之外的trials,以及2名错误率高于35%的被试数据(分别为37.5%和46.3%)(Meert et al., 2009),对剩下的trials进行数据分析,总的正确率为95.64%,总的平均反应时为2789.36ms。具体见表 2。
| 分数对类型 | 正确率(%) | 反应时(ms) | ||
| 平均数 | 标准差 | 平均数 | 标准差 | |
| 同分母 | 98.77 | 3.75 | 1305.18 | 406.49 |
| 同分子 | 95.27 | 8.82 | 1970.33 | 822.23 |
| 异分子异分母 | 92.89 | 7.40 | 5092.57 | 2035.49 |
在正确率和平均反应时上分别对三类分数对进行单因素重复测量方差分析。结果表明,在正确率上,分数对类型的主效应显著,F(2,100)=9.97,p<0.001,偏η2=0.17。事后比较发现,同分母分数对的正确率显著高于其他两类分数对(p<0.01),而同分子分数对和异分子异分母分数对之间的差异不显著(p>0.05)。在反应时上,三类分数对之间同样存在显著差异,F(2,100)=138.14,p<0.001,偏η2=0.73。事后比较发现,被试在同分母分数对上的反应速度要快于其他两类分数对(p<0.001),在同分子分数对上的反应速度要快于异分子异分母分数对(p<0.001)。
3.2 对口语报告策略的分析两名编码者对策略归类的评判具有较高的一致性,Kappa系数均值为0.93。
在具有共同成分(即同分母与同分子)的两类分数比较任务中,被试均使用他们熟知的比较规则,即“分母相同,看分子,分子越大,分数越大;分子相同,看分母,分母越大,分数越小”,也就是只比较分子/分母大小的策略。从策略的角度分析,被试比较同分子和同分母分数对时,都是成分加工模式。而对于异分子异分母分数比较任务,794个口语报告策略中有5种分数比较策略被使用(表 3)。
| 策略类型 | Trials | 使用人数a | 使用最多的刺激b | 反应时均值(ms)c | 正确率c |
| 通分 | 22.42% | 26 | 1/7_2/9(16) | 6307.74 | 93.8% |
| 交叉相乘 | 44.46% | 31 | 5/6_4/7(27) | 4420.97 | 92.3% |
| 剩余策略 | 4.66% | 14 | 5/6_7/8(9) | 4700.43 | 89.1% |
| 标杆策略 | 15.37% | 24 | 1/2_3/7(18) | 4067.77 | 95.9% |
| 化为小数 | 10.33% | 14 | 1/4_2/5(8) | 6757.57 | 90.2% |
| 其他 | 2.77% | 9 | 3/5_2/7(3) | 4162.77 | 90.9% |
| 注:a指选择使用该策略至少1次的人数;b指在所有刺激中使用该策略人数最多的刺激,括号为使用人数;c为出现该策略下所有trials的反应时均值和正确率。 | |||||
按照被试口语报告策略所包含的实际加工过程以及已有研究的结果,上述策略可分别归属于成分加工模式及整体加工模式:通分、交叉相乘和剩余策略属于基于成分加工的策略,占Trial总数的71.54%;标杆策略和化为小数策略属于基于整体加工的策略,占Trial总数的25.70%。对基于两种加工模式的策略进行卡方检验结果表明,基于成分加工的策略的使用显著多于整体策略(χ2(1,773)=168.59,p<0.01),从策略的角度分析,被试比较异分子异分母时,是混合加工模式,其中成分加工模式占主导地位。
为了进一步验证上述结论,将基于距离效应和问题大小效应对反应时做进一步分析。
3.3 对三类分数比较任务反应时的回归分析由于整体错误率很低(4.36%),加之正确率与反应时的相关系数为0.02(p<0.05),不存在速度—准确性代偿问题,因此对正确率不再做进一步分析(Zhou,Chen,Chen,& Dong,2008; 辛自强,李丹,2013)。剔除错误反应的trials,对剩下的反应时数据进行分析。回归分析的方法与已有研究的分析范式一致(Faulkenberry & Pierce, 2011; Meert et al., 2009)。首先,将每个距离指标作为预测变量,分别对反应时进行单一线性回归,以考察各预测变量在反应时上的距离效应和问题大小;其次,若多个预测变量都显著,则同时放入回归方程,以评估它们对反应时的相关贡献。
对同分子分数比较任务的单一回归分析结果(表 4)表明,两个分数的实值距离的预测作用显著,R2=0.01,β=-0.10,t =-2.01,p<0.05;成分距离的预测作用显著,R2=0.03,β=-0.17,t =-3.34,p<0.01。将两者同时放入回归方程,结果表明,成分距离显著预测反应时(R2=0.03,β=-0.19,t =-2.69,p<0.01),实值距离不再显著预测反应时(β=0.03,t =0.40,p>0.05)。这些结果说明随着成分距离(分母之间的差值)的增加,被试的反应速度加快,被试在比较分数时采用的是成分加工模式。对于同分母分数比较任务的单一回归分析结果表明,成分距离和实值距离作为反应时的预测变量主效应均不显著,无法判断成分距离和实值距离对反应时的预测作用。
| 分数对类型 | 回归类型 | 预测变量 | F | R2 | β | t | p |
| 单一回归 | 实值距离 | 4.03 | 0.01 | -0.1 | -2.01 | 0.04* | |
| 同分子 | 成分距离 | 11.2 | 0.03 | -0.17 | -3.34 | 0.001 *** | |
| 多元回归 | 实值距离 | 5.67 | 0.03 | 0.03 | 0.4 | 0.69 | |
| 成分距离 | -0.19 | -2.69 | 0.01** | ||||
| 同分母 | 单一回归 | 实值距离 | 0.26 | 0 | 0.03 | 0.51 | 0.61 |
| 成分距离 | 0.09 | 0 | 0.02 | 0.31 | 0.76 | ||
| 交叉乘积均值 | 24.2 | 0.03 | 0.18 | 4.92 | 0.001 *** | ||
| 单一回归 | 分母距离 | 5.19 | 0.01 | -0.08 | -2.28 | 0.02* | |
| 异分子异分母 | 分子距离 | 1.73 | 0 | -0.05 | -1.32 | 0.19 | |
| 实值距离 | 2.28 | 0 | -0.06 | -1.51 | 0.13 | ||
| 多元回归 | 交叉乘积均值 | 12.32 | 0.03 | 0.17 | 4.39 | 0.001 *** | |
| 分母距离 | -0.03 | -0.68 | 0.5 |
对于异分子异分母分数比较任务的单一回归分析结果表明:两个分数的交叉乘积均值预测作用显著(R2=0.03,β=0.18,t =4.92,p<0.01);两个分数之间成分距离(即分母差距)预测作用显著(R2=0.01,β=-0.08,t =-2.28,p<0.05)。将两者同时放入回归方程(R2=0.03),对反应时的多元回归结果显示,交叉乘积均值是显著预测变量(β=0.17,t =4.39,p<0.00),分母距离不再显著预测反应时(β=-0.03,t =-0.67,p>0.05)。这些结果说明随着交叉乘积均值的增加,被试的反应速度变缓,问题大小效应说明被试在比较分数时采用的是成分加工模式。
对不同类型分数对中各个预测变量的相关分析结果表明:预测变量之间的相关程度在不同分数对类型中是变化不定的,如同分子分数对实值距离和成分距离之间相关较低(r=0.34,p<0.05),同分母分数对实值距离和成分距离之间相关较高(r=0.69,p<0.01),异分子异分母各预测变量之间相关见表 5,因此,有必要根据被试口语报告的策略进行进一步分析。
| 变量 | 1 | 2 | 3 | 4 | |
| 1.交叉乘积均值 | — | ||||
| 2.分母距离 | -0.33** | — | |||
| 3.分子距离 | 0.06 | 0.76** | — | ||
| 4.实值距离 | -0.06 | 0.02 | 0.23** | — | |
| 注:* p<0.05; ** p<0.01; ***p<0.001,下同 | |||||
为了进一步分析被试的分数比较策略与反应时预测的加工模式的一致性,按照策略所属类型(成分加工与整体加工)对异分子异分母的总体trials进行分类,并对两类加工模式的反应时做同样的回归分析,单一回归分析结果(表 6)表明,在被试以基于成分加工的策略完成的trials下,交叉乘积均值作为反应时的预测变量效应显著(R2=0.03,β=0.19,t =4.32,p<0.001)。也就是说被试用基于成分加工的策略时,并不依赖分数的实际整体大小。而在以基于整体加工的策略完成的trials下,单一回归分析发现了比较有趣的结果,作为成分加工模式指标的交叉乘积均值和分母距离均显著,交叉乘积的均值具有更大的影响力,作为整体加工模式指标的实值距离却不显著。
| 策略类型 | 交叉乘积均值 | 分子距离 | 分母距离 | 实值距离 |
| 成分 | 0.19*** | -0.03 | -0.05 | -0.08 |
| 整体 | 0.23*** | -0.11 | -0.19** | 0.01 |
从本研究结果可知,对于同分子分数,被试口语报告所采用的是成分策略,同时成分距离(分母间距离)对反应时具有显著预测作用,来自直接和间接的证据表明小学生比较同分子分数对时会采用成分加工模式,这与Bonato等人(2007)的研究结果一致。但是在同类型的刺激材料下,Meert等人(2009,2010)对成人及儿童的研究结果却是整体加工模式。不一致的原因可能在于,Meert等人是混合呈现分数对,从加工分母成分到加工分子成分的转换需要消耗一定的认知成本和灵活性(Huber,Moeller,& Nuerk,2014),因而被试倾向于采用加工分数整体值的方式来完成任务,是实验环境导致使用成分策略存在一定困难。而在本研究中,同分子的分数刺激与同分母的分数刺激是分开呈现的,被试先完成其中一项分数对比任务,再完成另一项。因此被试在单一同分子分数对的情景下,很容易找到仅仅选择分母较小的分数为目标反应的规律。
对于同分母分数,口语报告的结果表明小学生采用的是成分加工模式,与现有的反应时结果一致(Meert et al., 2009,2010; Obersteiner et al., 2013)。这样的结果与同分母分数自身属性有关,分子成分的大小与分数值大小是一致的,因此被试仅仅比较分子就能正确完成任务。
在异分子异分母分数比较任务下,口语报告的策略表明,被试主要采用成分加工模式,且对反应时回归分析的结果也验证了这一结论,这与Schneider和Siegler(2010)的整体加工模式结果不完全一致。在多数情况下,被试选择了所偏好的、更方便的成分加工策略,这就部分否认了“在分数对无规律的情况下,被试很难生成成分加工策略”的说法(Meert et al., 2009; Schneider & Siegler, 2010)。
加工模式的形成可以说是分数对类型和被试的策略相结合的结果(Faulkenberry & Pierce, 2011)。从口语报告看来,基于成分加工的策略在分数比较策略中占主导地位,同时反应时回归分析结果也证明了作为整体加工指标的实值距离并未对反应时有显著性贡献,两者共同说明:六年级的被试在不同类型分数比较任务中,主要采用成分加工模式,而非整体加工,表明具有分数基本知识的小学生,倾向于利用分数的整数成分来完成比较任务,而回避了对分数实值的判断,这是利用自然数知识正确解决分数比较任务的倾向。Schleppenbach等人(2007)的跨文化研究指出,在中国的数学课堂上,教师更重视规则的教学,经过大量练习,学生已将基本规则内化,比如对比有共同成分的分数时,采用“分子相同比较分母,分母小,分数大;分母相同比较分子,分子大,分数大”这一规则。因此在进行分数比较时,充分利用这些有效规则,形成定势,成分加工倾向受此定势的影响。对此,脑神经研究作了进一步解释,Cohen和Walsh(2009)假设了一个数字表征的双加工模型,初始存在一个与呈现材料表面形式直接相关的自动化表征,随后这种自动化表征会根据被试自身资源和任务需求等而被有意识地影响。也就是说初始的自动化表征依赖于分数的离散成分,当仅靠分数成分不能完成任务后,就需要进入数量精细加工阶段,再通过运算获得分数的整体实值值。本研究结果表明,即使被试采用了整体加工策略,也是显著受到了成分距离与问题大小的影响,这意味着被试可能是先通过对分数成分加工之后再进行整体加工的,即成分加工优先于整体加工。
另外,本研究采用的是符号系统的分数材料,小学生在对两个分数进行大小比较时,只是符号水平上的加工,因此得出成分加工的结论。辛自强和李丹(2013)通过对非符号分数材料的加工模式进行探讨,发现被试采用的是整体加工模式,也就是在脱离分数符号的情境中采用的是整体加工模式。若将分数的比较任务推广到有意义的实际生活情境,比如描述切蛋糕这样一种实际生活情境,让人们选择蛋糕的大小,这时候人们采用的是什么样的加工模式呢?还会继续考虑蛋糕所代表分数符号的整数成分吗?这些问题尚需进一步的研究。
4.2 来自反应时和口语报告策略证据的比较从本研究的结果可知,来自口语报告的策略(直接证据)与对反应时回归分析结果(间接证据)并非完全吻合。在同分子类型下,两方面的证据同时证明被试加工分数的成分;而在同分母类型下,成分距离(分子差距)或实值距离均无法解释被试的反应时变异,而口语报告证据表明被试采用成分加工策略;在异分子异分母分数比较任务中,口语报告证据表明被试既采用成分加工策略又采用整体加工策略,并且成分加工占主导地位,然而,从对基于两类加工的策略的反应时的回归分析结果可知,在被试以基于成分加工的策略完成的trials中,反应时回归分析结果支持了被试对分数进行成分加工,而在以基于整体加工的策略完成的trials中,反应时回归分析结果依然支持被试对分数进行成分加工。
如何解释两方面证据的不完全一致性呢?一方面大部分被试并不是采用单一策略来完成任务,因此从材料的呈现到被试做出反应期间既包含了策略选择又包含了策略的执行,两者并未独立地区分出来,这使得对反应时差异的解释复杂化。另一方面,整体加工策略下需要先对分数的成分进行加工,再比较分数的大小,或者与标杆分数比较大小,这意味着比较实值值大小的时间并不纯粹受某一种加工模式影响,因此用实值距离对反应时的变异作解释是毫无意义的。同分母分数对中对反应时的回归分析并未验证距离效应,无法通过此方法确认被试在该分数类型下的加工模式;在异分子异分母类型中,被试报告的是整体加工策略,但从反应时的回归分析证据来看却是成分加工模式,即来自两方面的证据没有很好的吻合,甚至出现了相反的结论。此外,根据结果3.3,在不同类型的分数对中,分数之间的实值距离与成分距离的相关性确实如同前言中所分析那样是不一致的。由此可以推断,通过对反应时或正确率做回归检测距离效应得出加工模式——这样的一种研究范式并不稳定,这种范式的不稳定性可能导致了先前研究对分数加工模式的结论的不一致性。
5 结论(1) 在不同类型分数比较任务中,小学生均采用成分加工模式,而非整体加工模式。
(2) 口语报告的策略与反应时回归分析结果并不完全吻合,侧面证明原有研究方法的不稳定性。
| Ashcraft M.H (1992). Cognitive arithmetic: A review of data and theory. Cognition , 44(1), 75-106. |
| Bonato M., Fabbri S., Umiltà C., & Zorzi M (2007). The mental representation of numerical fractions: Real or integer?. Journal of Experimental Psychology: Human Perception and Performance , 33(6), 1410-1419. DOI: 10.1037/0096-1523.33.6.1410. |
| Clarke D.M., & Roche A (2009). Students' fraction comparison strategies as a window into robust understanding and possible pointers for instruction. Educational Studies in Mathematics , 72(1), 127-138. DOI: 10.1007/s10649-009-9198-9. |
| Cohen Kadosh R., & Walsh V (2009). Numerical representation in the parietal lobes: abstract or not abstract?. Behavioral and Brain sciences , 32(3), 313-328. |
| Faulkenberry T.J., & Pierce B.H (2011). Mental representations in fraction comparison: Holistic versus component-based strategies. Experimental psychology , 58(6), 480-489. DOI: 10.1027/1618-3169/a000116. |
| Huber S., Moeller K., & Nuerk H.C (2014). Adaptive processing of fractions — Evidence from eye-tracking. Acta Psychologica , 148(3), 37-48. |
| Liu C., Xin Z., Lin C., & Thompson C.A (2013). Children's mental representation when comparing fractions with common numerators. Educational Psychology , 33(2), 175-191. DOI: 10.1080/01443410.2012.730324. |
| Meert G., Grégoire J., & Noël M (2009). Rational numbers: Componential versus holistic representation of fractions in a magnitude comparison task. The Quarterly Journal of Experimental Psychology , 62(8), 1598-1616. DOI: 10.1080/17470210802511162. |
| Meert G., Grégoire J., & Noël M (2010). Comparing the magnitude of two fractions with common components: Which representations are used by 10-and 12-year-olds?. Journal of Experimental child psychology , 107(3), 244-259. DOI: 10.1016/j.jecp.2010.04.008. |
| Moyer R.S., & Landauer T.K (1967). Time required for Judgements of Numerical Inequality. Nature , 215(5109), 1519-1520. DOI: 10.1038/2151519a0. |
| Obersteiner A., Van Dooren W., Van Hoof J., & Verschaffel L (2013). The natural number bias and magnitude representation in fraction comparison by expert mathematicians. Learning and Instruction , 28(4), 64-72. |
| Schleppenbach M., Perry M., Miller K.F., Sims L., & Fang G (2007). The answer is only the beginning: Extended discourse in Chinese and US mathematics classrooms. Journal of Educational Psychology , 99(2), 380-396. DOI: 10.1037/0022-0663.99.2.380. |
| Schneider M., & Siegler R.S (2010). Representations of the magnitudes of fractions. Journal of Experimental Psychology: Human Perception and Performance , 36(5), 1227-1238. DOI: 10.1037/a0018170. |
| Sprute L., & Temple E (2011). Representations of fractions: Evidence for accessing the whole magnitude in adults. Mind, Brain, and Education , 5(1), 42-47. DOI: 10.1111/j.1751-228X.2011.01109.x. |
| Zhang L., Fang Q., Gabriel F.C., & Szücs D (2014). The componential processing of fractions in adults and children: Effects of stimuli variability and contextual interference. Frontiers in Psychology , 5(3), 250-253. |
| Zhou X., Chen C., Chen L., & Dong Q (2008). Holistic or compositional representation of two-digit numbers? Evidence from the distance, magnitude, and SNARC effects in a number-matching task. .Cognition , 106(3), 1525-1536. DOI: 10.1016/j.cognition.2007.06.003. |
| 辛自强, 李丹. (2013). 小学生在非符号材料上的分数表征方式. 心理科学 , 36(2), 364-371. |
 2016, Vol. 32
2016, Vol. 32

