2016, Vol. 32
表1(Table 1)
不同任务类型条件下4~6年级儿童比例推理策略的表现
http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2016.04.01
国家教育部主管、北京师范大学主办。
国家教育部主管、北京师范大学主办。
文章信息
- 赖颖慧, 尹称心, 陈英和 .2016.
- LAI Yinghui, YIN Chenxin, CHEN Yinghe .2016.
- 不同任务类型条件下4~6年级儿童比例推理策略的表现
- The Performance of Proportional Reasoning Strategies of Children in grade 4 to 6 under Different Types of Tasks
- 心理发展与教育, 32(4): 385-393
- Psychological Development and Education, 32(4): 385-393.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2016.04.01
引用本文
赖颖慧, 尹称心, 陈英和 . 2016. 不同任务类型条件下4~6年级儿童比例推理策略的表现[J]. 心理发展与教育, 32(4): 385-393
LAI Yinghui, YIN Chenxin, CHEN Yinghe . 2016. The Performance of Proportional Reasoning Strategies of Children in grade 4 to 6 under Different Types of Tasks[J]. Psychological Development and Education, 32(4): 385-393.
不同任务类型条件下4~6年级儿童比例推理策略的表现
1. 首都体育学院, 教育学与心理学教研室, 北京 100191
;
2. 深圳市龙岗区布吉中学, 深圳 518172 ;
3. 北京师范大学, 发展心理研究所, 北京 100875
2. 深圳市龙岗区布吉中学, 深圳 518172 ;
3. 北京师范大学, 发展心理研究所, 北京 100875
摘要:
随机选取小学4~6年级被试86名，从辅助策略、比例推理策略的策略选择和策略效用三方面，通过五种类型的天平任务考察儿童比例推理策略的表现。结果表明：（1）儿童最常使用手指动作辅助加工基本数量信息。辅助策略的使用率随年龄增长而减少，五年级开始使用出声思维，反映出元认知能力的发展。（2）在正式学习比例知识之前，各年级儿童都能使用两种以上策略，也能根据任务难度自发产生新策略，具备策略选择的多样性和适应性。其中，三个年级均能使用定性比例推理策略（双维策略，IIIA策略，补偿策略），表明儿童初步认识了距离和重量两个维度的共变关系。此外，六年级儿童能使用“运货车策略”将冲突问题灵活地化解为简单问题。（3）儿童的错误策略表现为：在冲突任务中盲目使用补偿策略、简单策略或加法策略。（4）分层回归分析表明，在控制年龄后，儿童的一般推理能力越高，其对重量策略的依赖性越低，且可能更容易发掘距离维度的意义，其使用运货车策略的频次更多。此外，一般推理能力对解决冲突类天平任务的正确次数有正向预测作用。
关键词: 儿童 比例推理 策略发展 天平任务
The Performance of Proportional Reasoning Strategies of Children in grade 4 to 6 under Different Types of Tasks
1. The Teaching and Research Office of Education and Psychology, Capital University of Physical Education and Sports, Beijing, 100191
;
2. Buji Middle School, Shenzhen, 518172 ;
3. The Institution of Development Psychology, Beijing Normal University, Beijing, 100875
2. Buji Middle School, Shenzhen, 518172 ;
3. The Institution of Development Psychology, Beijing Normal University, Beijing, 100875
Abstract:
This study investigated the developmental characteristics of children's proportional reasoning in general domain by balance scale task. Eighty-six 4th to 6th graders in a primary school from Beijing were chosen. The results indicated: (1) Children used support strategies to help them represent problems. They use finger strategy to process basic information of numbers, and this strategy decreased with age. Children in grade 5 began to use think aloud protocol, which showed the development of children's metacognition; (2) Before the formal education of proportional reasoning, the children can use more than two kinds of strategies, and they can develop new strategies automatically. Children can use qualitative proportional reasoning strategies (two-dimensional strategy, compensatory strategy, IIIA strategy). It means that children recognized the co-variation of distance and weight. In addition, children in grade 6 used buggy strategy in conflict problems. With the buggy strategy they transferred complicated tasks into simple tasks. (3) The characteristic of children's wrong strategies were as follows: using compensatory strategy blindly in conflict circumstances, or using simple strategies and additive strategies to solve conflict tasks. (4) Hierarchical regression analysis shows that, after controlling age, the children with higher general reasoning ability depend less on weight strategy, and they use more distance strategy and the buggy strategy. In addition, the general reasoning ability positively predicts the correct times of the conflict problems.
Key words: children proportional reasoning strategy development the balance scale task
1 引言
3.2 不同任务类型条件下的比例推理策略选择的表现
3.2.1 策略选择多样性的表现
3.3 不同任务类型条件下的比例推理策略效用表现
4 讨论
4.1 儿童解决五类天平任务的辅助策略表现
比例(proportion)是表示两个比值相等的式子，如3:4 = 9:12；其特性是两外项之积等于两内项之积。比例推理(proportional reasoning)是指根据已有的数量信息并依照比例的特性，判断比例是否成立的过程。对比例项乘积关系的理解是解决比例推理问题的关键所在(Cramer & Post，1993)。
比例推理策略的研究范式多样。多数研究采用数学学科领域的研究范式：缺失值任务，如经典的高矮人问题(Karplus，Karplus， & Wollman，1974)；数值比较任务，如经典的橘子汁问题(Noelting，1980)；定性预测和比较等(Heller，Post，Behr， & Lesh，1990)。比例推理还存在于更综合的问题情境中。如比例尺问题(Akatugba & Wallace，2009)，溶液混合问题(Boyer，Levine， & Huttenlocher，2008)和天平(平衡尺)问题(Akatugba & Wallace，2009)等。
在上述范式中，天平问题代表了需要整合两个量化维度信息的问题(Dandurand & Shultz，2014)，体现了一般领域内的问题情境对比例推理能力的需求(Jansen & van der Maas，2002)。该任务涉及两个维度：天平两端的重物重量与重物到支点的距离。成功解决天平问题在于对重量与距离的比例关系(重量1：重量2 = 距离2：距离1)做出恰当的编码分析。天平任务集中反映了科学思维与数学思维的联系，这种思维联系是促进科学课程学习的关键因素(Akatugba & Wallace，2009)。有鉴于此，本研究将以天平任务为载体，从解题的辅助策略、策略选择及策略效用三个方面，以及一般推理能力与比例推理表现的关系角度，系统分析4~6年级儿童在五种任务类型条件下的比例推理策略表现。
首先，辅助策略能减轻工作记忆负荷，帮助问题表征，并侧面反映儿童思维发展的特点；以往研究未充分重视解题的辅助策略分析。本研究将编码手指动作、纸笔、出声思维等辅助策略，考察辅助策略类型和使用频次的发展特点。
其次，婴幼儿及学龄儿童在解决同一个问题时均不局限于某种特定策略(Coyle & Bjorklund，1996)。Siegler等(1999)提出了解释多种策略共存现象的“重波模型”(刘电芝和杨会会，2008)，并认为策略多样性广泛存在(Siegler & Jenkins，2014)。据此，本研究假设儿童能选用两种以上策略解决同一类天平问题，也能用多种策略解决不同类型的天平问题，具备策略选择的多样性；并假设儿童能根据任务难度自发产生新策略，具备策略选择的适应性。
以往研究表明，儿童解决天平任务所选择的主要策略如下。最初，Siegler等人(1976)发现了四种典型的比例推理策略：简单重量策略、简单距离策略、双维策略和乘法策略。后续研究提出了加法策略和定性比例推理策略(Jansen & van der Maas，2002)，其中，定性比例推理策略包括双维策略，IIIA策略和补偿策略等(Normandeau，Larivée，Roulin， & Longeot，1989)。
以上策略主要是用规则评定法(Rule Assessment Methodology，Siegler，1976)和分层多项选择法(Hilton，Hilton，Dole， & Goos，2013)进行划分的，两类方法并未充分挖掘策略类型。为了更充分地判断被试的策略类型，本研究将以前人研究为基础，采用编码分析法，划分出八种策略类型，并将它们归入四种策略水平，以期更系统地考察儿童比例推理策略选择情况，同时发展比例推理策略的分类方法。
再次，考察比例推理中的错误策略有助于认识儿童解决该类问题的难点(Boom & Hoijtink，2001; Quinlan，Van，Jansen，Booij， & Rendell，2007)，因此本研究将分析儿童的错误策略特点。此外，将分析儿童解决各类天平任务的正确次数和解题时间，以考察各年级的比例推理策略效用表现。
最后，本研究还关注儿童的一般推理能力与比例推理策略的选择及效用的关系。以往研究常用瑞文标准推理测验测查智力g因素或流体智力，而新近研究(Gignac，2015)表明瑞文测验与g因素的共变率仅为50%，与流体智力的共变率仅接近10%。且由于完成瑞文测验需要归纳推理和类比推理共同参与，故本研究将瑞文标准推理测验分数作为一般推理能力的测量指标，考察一般推理能力与比例推理的策略表现的关系。
综上，考察儿童使用辅助策略的特点及其比例推理策略选择的多样性与适应性，能揭示其思维品质，并为策略发展的重波模型等理论提供实证支持；对策略进行系统的编码分析能丰富比例推理的策略类型研究。此外，比例推理是连接小学与中学数学教育的重要知识点，是解决数学等学科复杂问题的必备运算能力(Johnson，2013; Akatugba & Wallace，2009)。探明比例推理策略类型的发展特点及错误策略的使用特点，有助于教师依据学生的学习准备状态选择教学方法。最后，分析一般推理能力与比例推理的关系，能为深入探索不同类型和不同层次的推理能力的关系提供思路。
2 研究方法采用3(年级：四、五、六年级)×5(题目类型：简单重量、简单距离、冲突重量、冲突距离、冲突平衡)的混合设计，其中题目类型是组内变量。记录儿童的正确次数、解题时间、辅助策略及口语报告。采用张厚粲等人(1989)修订的《瑞文标准推理测验》考察儿童的一般推理能力。
2.1 被试由于国外对比例问题的教学始于六、七年级(Adjiage & Pluvinage，2007；Jitendra，Star，Dupuis， & Rodriguez，2013)，我国数学课程标准也要求小学六年级下学期开展比例尺问题的教学；为了控制任务熟悉度的影响，本研究在学年的上学期取样。
随机抽取北京市某普通小学4 ~ 6年级儿童101名，排除未能完成全部任务的15人，得到有效被试86名：四年级30人(M = 10.23岁，SD = 0.34；男12人)，五年级28人(M = 11.21岁，SD = 0.25；男12人)，六年级28人(M = 12.37岁，SD = 0.35；男15人)。
2.2 任务首先，以班级集体施测的方式测查了瑞文测验。然后，对天平任务进行个别施测。采用Visual Basic程序编制天平任务，该任务共30项，其中前5项为练习试次。正式测验为：简单重量任务(W)、简单距离任务(D)、冲突重量任务(CW)、冲突距离任务(CD)和冲突平衡任务(CB)各5项。任务编排见附录。
2.3 程序正式实验由2名主试主持。主试A控制实验过程，主试B观察和记录被试解题过程中的反应，详细记录被试的口语报告。简要流程如下：
(1) 主试A读指导语：“小朋友，你好！我们来做一个天平的游戏，请你判断一下天平将向哪边倾倒。请做出判断并说答案，然后我会问你是怎么做的。……好了，我们先来熟悉一下天平任务。”
(2) 讲解天平任务。图 1左：“你看，中间这个就是天平，天平上每一小格的距离是相等的。右下角是砝码，每个砝码的重量是一样的，当天平左右两边砝码的重量不等时，天平就会向一边倾倒。左下角的是支撑物，它用来保持天平稳定。”图 1右：“这张图就是支撑物的作用。下面我们将给你看一张图片，问题是‘当去掉两个支撑物时，天平会向哪边倾倒？’明白了吗？”……“好，先来练习几道题”。
|
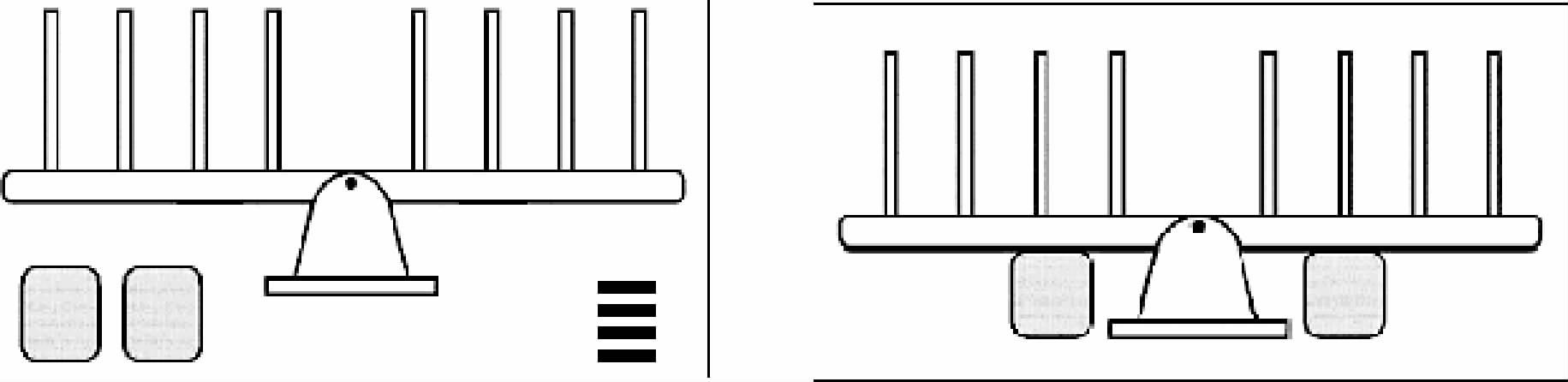
| 图 1 天平任务图例 |
(3) 让儿童练习5道题，然后开始正式实验。
(4) 正式测验时，题目出现则开始计时，被试说出答案的同时主试A按键停止计时。
(5) 主试A输入被试的答案。然后追问，“你是怎么得到这个结果的”。主试B详细观察被试的计算过程，并记录其口语报告内容及辅助策略。
2.4 策略编码我们基于前人的研究成果(Jansen & van der Maas，2002; Zelazo & Müller，2002; Normandeau，Larivée，Roulin， & Longeot，1989)，编制了儿童解决天平任务的比例推理策略编码表(表 1)。
表 1 天平任务的比例推理策略编码表
| 策略水平 | 策略种类 | 说明 |
| 水平一 | 重量策略 | 仅根据重量或砝码的多少判断。 |
| 距离策略 | 仅根据砝码距支点的远近判断。 | |
| 双维策略 | 能意识到重量和距离都对天平倾斜起作用，但只有当一个维度相等时(如距离)，才根据另一个维度(如重量)进行判断。 | |
| 水平二 | IIIA策略1 | 当距离和重量都不相等时，凭感觉线索进行判断，在一些冲突任务上觉得距离重要，而在另一些任务上则认为重量更重要。 |
| 补偿策略 | 在冲突问题上认为天平将保持平衡，因为他们认为一边的数量大弥补了另一边的距离远。 | |
| 水平三 | 加法策略 | 分别将天平两端的砝码数量和距离大小相加再进行比较，总和大的一端下沉，如果总数相等则天平将保持平衡。 |
| 运货车策略 | 在心理上移动砝码，砝码每向外移动一格，重量减少一个，直到左右砝码的位置相同，这样将冲突问题转化为简单问题，根据重量进行判断。 | |
| 水平四 | 乘法策略 | 分别将天平两端的砝码数量和距离相乘再比较，乘积大的一端将下沉。 |
| 注：该名称源自皮亚杰的推理策略分类 | ||
根据策略所涉及的维度，我们划分了如下四个策略水平，共八种策略。水平一：仅根据重量或距离维度进行判断，如重量策略和距离策略；口语报告为“左边砝码比右边多，所以左边会沉下去”。水平二：意识到重量和距离两个维度同时起作用，但只做了定性判断。如双维策略，IIIA策略，补偿策略；口语报告为“左边和右边砝码一样多，但左边比右边距离远，所以左边会沉下去”或“左边比右边砝码多，右边比左边距离远，好像是左边会沉下去”或“左边比右边砝码多，右边比左边距离远，所以平衡”；水平三：意识到重量和距离同时起作用，但以加减法判断，如使用加法策略和运货车策略；口语报告为“左边的砝码加距离是4，右边的砝码加距离是5，所以右边会沉下去”或“左边的砝码每往外移一格，相当于减掉一个砝码”。水平四：能用乘积的方式表示两个维度的关系，做出正确判断；口语报告为“左边的距离乘以砝码数大于右边的距离乘以砝码数，所以左边会沉下去”。
两名主试根据策略编码表对儿童的口语报告进行编码。评分者信度Kappa系数均值为0.92，说明主试对策略类型的评判可靠性较高。被试的反应时、正误判断由计算机自动录入Excel文档，所有数据采用SPSS 18.0软件分析。
3 结果首先，分析了被试在解决天平任务时的辅助策略的发展特点。然后，从策略多样性和任务适应性两方面分析了各年级儿童比例推理策略选择情况。此外，通过3(年级)×5(任务类型)的重复测量方差分析，从解题时间和正确次数两方面分析了比例推理策略效用的表现。最后，以年龄和瑞文测验得分为预测变量，各类比例推理策略的种数、使用频次和各任务的解题时间及正确次数分别为结果变量，进行了分层回归分析，考察了一般推理能力与比例推理策略表现的关系。
3.1 不同任务类型条件下的辅助策略表现被试在解决五类天平任务时均主要借助了纸笔辅助运算、用手指在电脑屏幕上移动辅助思考及出声思维三种辅助策略。由图 2可知，儿童使用次数最多的是手指动作，其次为出声，最少的是纸笔运算，使用次数的差异显著，x2(4)= 11.05，p＜0.05。且辅助策略具有年级差异，x2(4)= 59.64，p ＜ 0.001(图 3)，手指策略随年级升高而迅速减少，出声思维逐步增多，三个年级均很少使用纸笔运算。
|
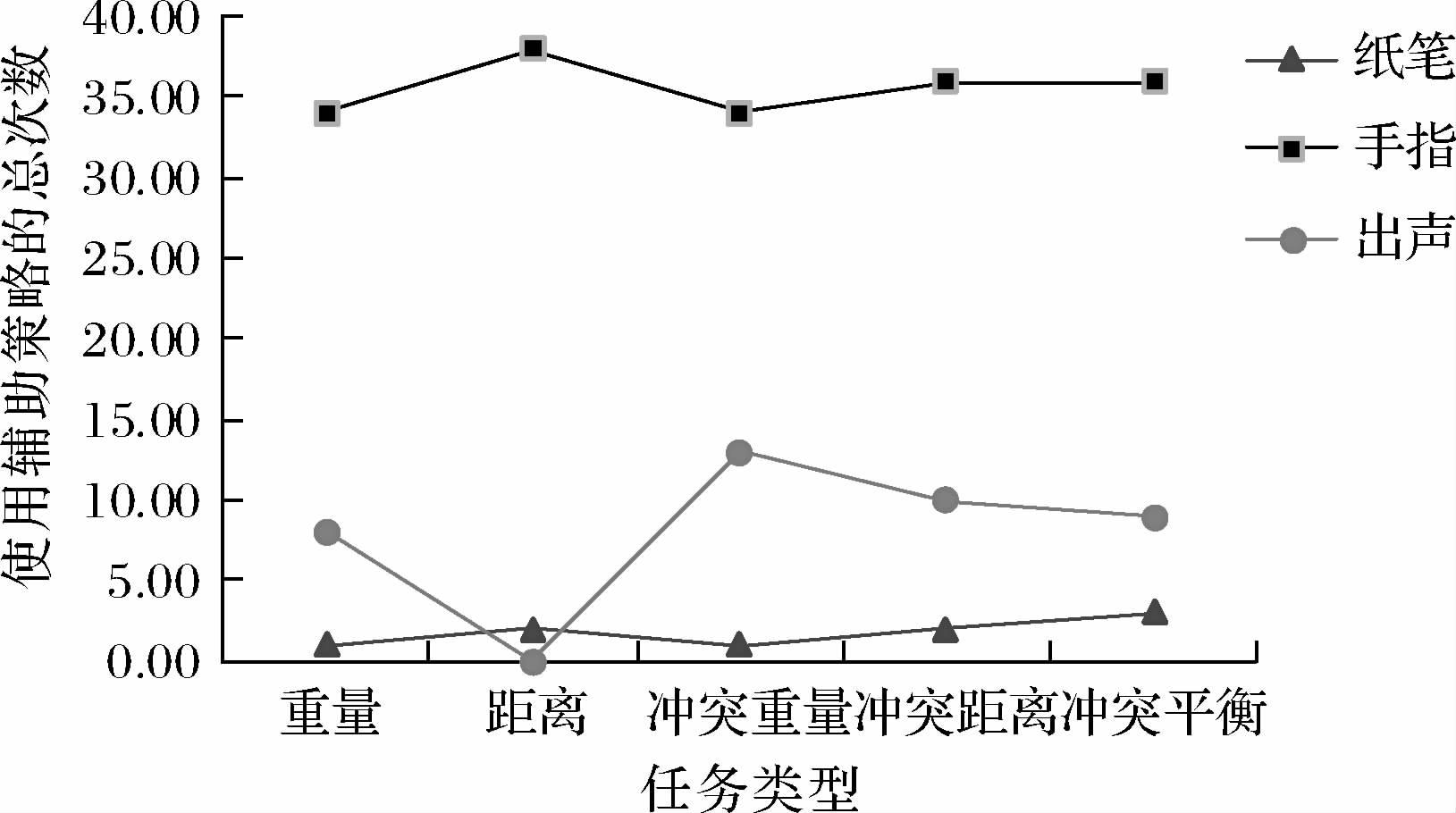
| 图 2 不同任务类型的辅助策略次数 |
|
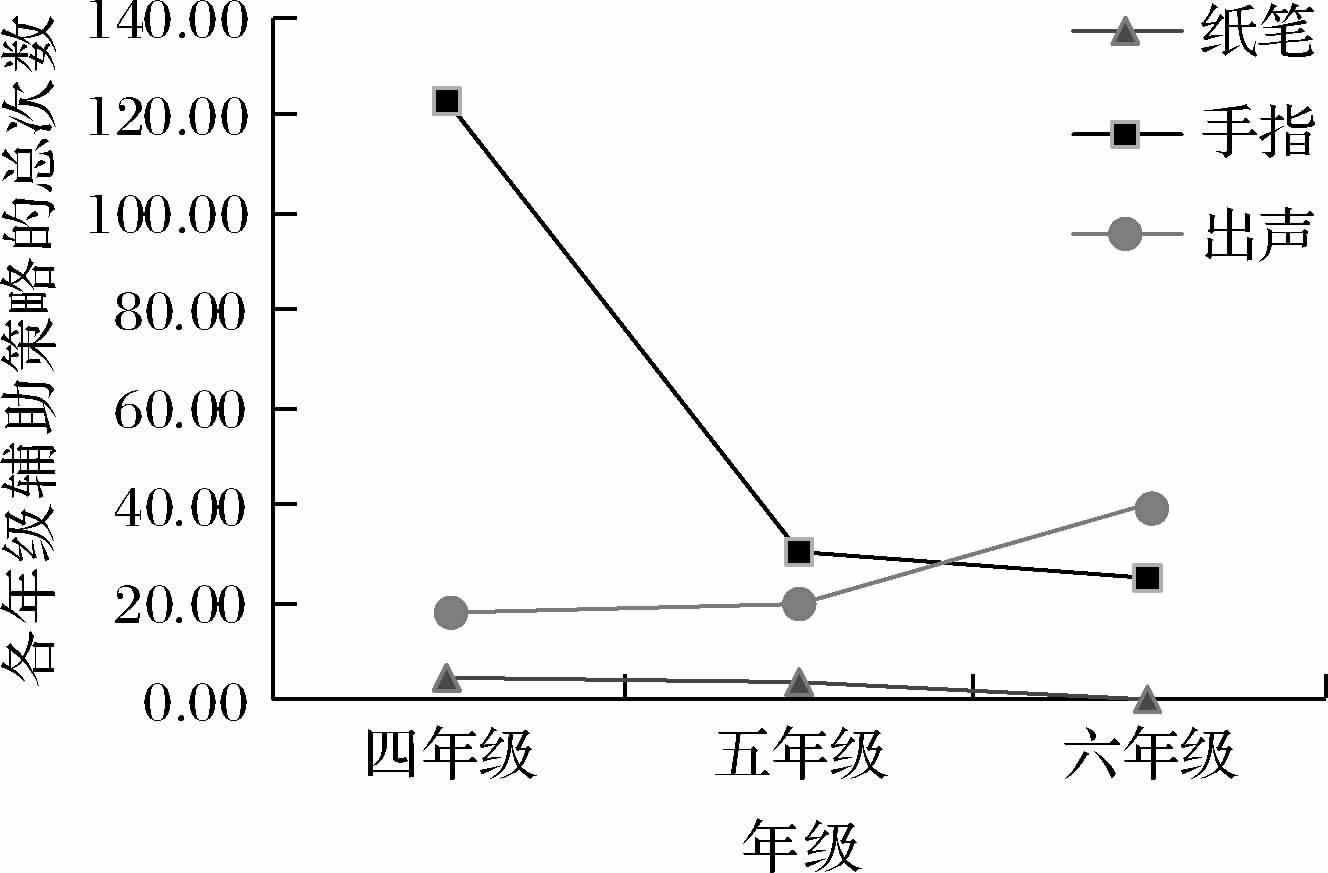
| 图 3 不同年级儿童的辅助策略次数 |
首先，根据儿童的操作步骤及口语报告，94.7%的儿童使用了两种以上的策略，且在同种任务类型下也会使用不同策略；随着任务难度增加，其所选择的策略种类随之增加。对被试所用的策略种类数(1~7种)和年级进行7×3的列联表分析，得出策略多样性的年级差异显著，x2 (12)= 21.57，p＜0.05。其中，四年级儿童多使用4种策略(27.3%)，五年级多使用6种策略(38.7%)，六年级多使用5种策略(27.3%)。
3.2.2 不同任务类型下的策略选择适应性表现首先，各策略选择频次的年级分布如图 4，四、五年级主要使用重量策略(47.4%，41.9%)；五年级开始使用乘法策略(2.3%)；六年级重量策略的使用次数减少，其他策略有所增加。其中，处于水平一的重量策略的使用频次随年级升高而逐渐下降，x2(2)= 49.62，p ＜ 0.001；距离策略的年级特点呈“U型”，x2(2)= 27.12，p ＜ 0.001。处于水平二的定性比例推理策略使用频次无年级差异(ps > 0.05)。处于水平三的加法和运货车策略均随年龄增长而增加，x2(2)= 20.44，p ＜ 0.001；x2(2)= 33.12，p ＜ 0.001。处于水平四的乘法策略从五年级开始出现，直到六年级仍不是主要策略。
|
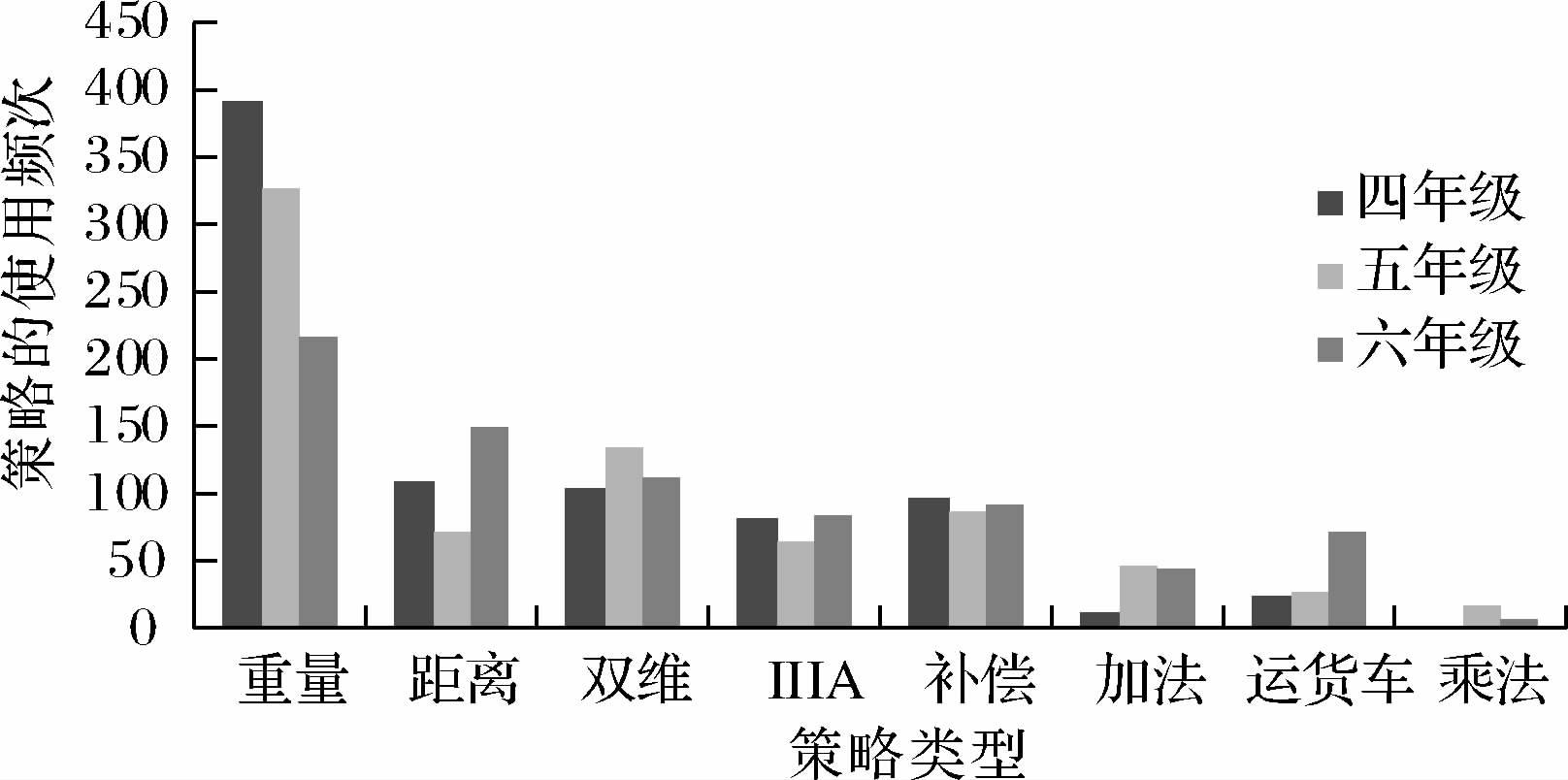
| 图 4 各年级儿童比例推理策略选择的频次分布 |
为了考察策略选择适应性的表现，对儿童在每类任务上的各策略使用频率分别做了年级差异检验。结果如表 2：儿童主要使用了处于水平一和水平二的策略。具体而言，儿童在简单重量/距离任务中，主要采用了重量/距离策略和双维策略；在冲突重量任务中主要选择重量和补偿策略；在冲突距离任务中主要选择重量和IIIA策略，距离策略和补偿策略其次；在冲突平衡任务中主要选择重量策略，补偿策略次之。卡方检验表明，儿童在简单重量任务中使用重量策略的比重明显高于其它任务。除乘法策略外，其它七种策略均存在显著的任务类型差异。
表 2 各年级儿童在各类任务中策略使用的频数和百分数(f，%)
| 任务类型 | 年级 | 指标 | 重量策略 | 距离策略 | 双维策略 | IIIA策略 | 加法策略 | 运货车策略 | 补偿策略 | 乘法策略 |
| 简单重量 | 四 | f | 154 | 4 | 47 | 3 | ||||
| % | 70.04% | 1.92% | 22.60% | 1.44% | ||||||
| 五 | f | 139 | 1 | 57 | 1 | |||||
| % | 70.20% | 0.51% | 28.79% | 0.51% | ||||||
| 六 | f | 145 | 1 | 50 | — | |||||
| % | 73.98% | 0.51% | 25.51% | — | ||||||
| x2 | 0.781 | 3 | 1.026 | 1 | ||||||
| 简单距离 | 四 | f | 38 | 51 | 54 | 10 | 4 | — | ||
| % | 24.20% | 32.48% | 34.39% | 6.37% | 2.55% | — | ||||
| 五 | f | 25 | 43 | 72 | 4 | 7 | 6 | |||
| % | 15.92% | 27.39% | 45.86% | 2.55% | 4.46% | 3.82% | ||||
| 六 | f | 9 | 83 | 58 | — | 5 | 3 | |||
| % | 5.70% | 52.53% | 36.71% | — | 3.16% | 1.90% | ||||
| x2 | 17.6 *** | 15.2 *** | 2.913 | 2.571 | 0.875 | 1 | ||||
| 冲突重量 | 四 | f | 88 | 12 | 20 | 3 | 7 | 35 | — | |
| % | 53.33% | 7.27% | 12.12% | 1.82% | 4.24% | 21.21% | — | |||
| 五 | f | 75 | 5 | 10 | 16 | 8 | 32 | 9 | ||
| % | 48.39% | 3.23% | 6.45% | 10.32% | 5.16% | 20.65% | 5.81% | |||
| 六 | f | 45 | 10 | 21 | 17 | 21 | 39 | 1 | ||
| % | 29.22% | 6.49% | 13.64% | 11.04% | 13.64% | 25.32% | 0.65% | |||
| x2 | 14.0 *** | 2.889 | 4.353 | 10.17** | 10.17** | 0.698 | 6.4* | |||
| 冲突距离 | 四 | f | 65 | 28 | 3 | 34 | 6 | 5 | 23 | — |
| % | 39.63% | 17.07% | 1.83% | 20.73% | 3.66% | 3.05% | 14.02% | — | ||
| 五 | f | 52 | 18 | 3 | 33 | 10 | 8 | 28 | 3 | |
| % | 33.55% | 11.61% | 1.94% | 21.29% | 6.45% | 5.16% | 18.06% | 1.94% | ||
| 六 | f | 24 | 39 | 1 | 40 | 3 | 23 | 22 | 3 | |
| % | 15.48% | 25.16% | 0.65% | 25.81% | 1.94% | 14.84% | 14.19% | 1.94% | ||
| x2 | 18.7 *** | 7.788* | 1.143 | 0.804 | 3.895 | 15.5 *** | 0.849 | 0 | ||
| 冲突平衡 | 四 | f | 91 | 14 | 1 | 15 | 4 | 8 | 31 | — |
| % | 55.49% | 8.54% | 0.61% | 9.15% | 2.44% | 4.88% | 18.90% | — | ||
| 五 | f | 79 | 4 | 2 | 16 | 21 | 5 | 23 | 5 | |
| % | 50.97% | 2.58% | 1.29% | 10.32% | 13.55% | 3.23% | 14.84% | 3.23% | ||
| 六 | f | 35 | 15 | 1 | 23 | 24 | 22 | 31 | 3 | |
| % | 22.73% | 9.74% | 0.65% | 14.94% | 15.58% | 14.29% | 20.13% | 1.95% | ||
| x2 | 25.4 *** | 6.72* | 0.5 | 2.11 | 14.2 *** | 14.1 *** | 1.506 | 0.5 | ||
| 注：* p ＜ 0.05，** p ＜ 0.001，*** p ＜ 0.001，下同。 | ||||||||||
表 3 儿童在5类天平任务下的解题时间(毫秒)的均值及标准差 M (SD)
| 年级 | 重量任务 | 距离任务 | 冲突重量任务 | 冲突距离任务 | 冲突平衡任务 |
| 四 | 6140.69(2222.60) | 9252.26(4806.96) | 9260.64(5303.97) | 10689.61(6740.54) | 9223.07(5358.95) |
| 五 | 5469.36(2355.22) | 8666.84(4403.72) | 10661.04(7420.38) | 9934.59(5315.98) | 9911.62(5052.11) |
| 六 | 4869.84(1853.62) | 6649.99(2763.45) | 11859.79(4866.64) | 10390.36(4982.20) | 10581.31(4291.51) |
表 4 儿童在5类天平任务下的正确次数的均值及标准差 M(SD)
| 年级 | 重量任务 | 距离任务 | 冲突重量任务 | 冲突距离任务 | 冲突平衡任务 |
| 四 | 4.97(0.18) | 3.50(1.91) | 3.37(1.83) | 1.97(1.88) | 1.03(1.35) |
| 五 | 4.93(0.38) | 3.82(1.70) | 3.11(1.73) | 1.93(1.46) | 1.50(1.62) |
| 六 | 5.00(0.00) | 4.61(1.20) | 2.07(1.72) | 3.07(1.51) | 2.32(1.87) |
3(年级)×5(任务类型)的重复测量方差分析表明，在解题时间上，仅任务类型的主效应显著，F(1，83)= 16.57，p ＜0.001，ηp2 = 0.17，其他效应皆不显著，ps ＞0.05。配对样本t检验表明，重量任务的解题时间显著短于距离任务，t(85)= -8.32，p ＜ 0.001，cohen’s d = -0.81，距离任务依次显著短于冲突重量，t(85)= -2.31，p ＜ 0.001，cohen’s d = -0.31，冲突平衡，t(85)= -3.55，p ＜ 0.001，cohen’s d = -0.33，及冲突距离任务，t(85)= -4.40，p ＜ 0.001，cohen’s d = -0.43；而三种冲突任务的解题时间没有显著差异，ps ＞0.05。
在正确次数上，任务类型和年级均有显著的主效应，F(4，332)= 64.68，p ＜0.001，ηp2 = 0.44；F(8，332)= 4.13，p ＜0.001，ηp2 = 0.09，任务类型与年级的交互作用显著，F(2，83)= 4.65，p＜0.05，ηp2 = 0.11。简单效应检验发现，重量任务的正确次数没有年级差异，p = 0.54；距离任务、冲突距离任务和冲突平衡任务的正确次数均表现为六年级显著高于四、五年级，F(2，83)=3.47，p＜0.05；F(2，83)= 4.44，p＜0.05；F(2，83)= 4.66，p＜0.05；冲突重量任务则表现出四、五年级显著高于六年级，F(2，83)= 4.32，p＜0.05。
3.4 一般推理能力对比例推理策略表现的影响为了考察一般推理能力与比例推理任务的关系，以年龄和瑞文测验的分数为预测变量，以五类天平任务的解题时间、正确次数、策略选择种数和策略使用频次分别为结果变量，进行了分层回归分析。在控制年龄后，瑞文测验得分对各类任务的解题时间的预测作用不显著，F(2，83): 0.47 ~ 4.76; β0: 0.02 ~ 0.18，t: 0.20 ~ 1.65，ps > 0.05，但对五类任务的策略选择种数均有显著的预测作用，F(2，83): 4.07 ~ 41.92; β0: 0.23 ~ 0.66，t: 2.38 ~ 8.71，ps ＜0.05。此外，瑞文测验得分对重量策略、距离策略和运货车策略的使用频次以及冲突任务的解题正确次数有显著的预测作用，见表 5。
表 5 瑞文推理测验分数对五类天平任务的策略使用频次与正确次数的预测
| ΔRp2 | F | df1 | df2 | η2 | β0 | t | |||
| 预测变量 | 瑞文分数 | ||||||||
| 结果变量 | 使用频次 | ||||||||
| 重量策略 | 0.16 | 16.19*** | 2 | 83 | 0.35 | -0.41 | -4.49*** | ||
| 距离策略 | 0.32 | 24.86*** | 2 | 83 | 0.54 | 0.57 | 6.77*** | ||
| 运货车策略 | 0.23 | 31.1*** | 2 | 83 | 0.68 | 0.48 | 5.93*** | ||
| 预测变量 | 瑞文分数 | ||||||||
| 结果变量 | 正确次数 | ||||||||
| 冲突重量任务 | 0.07 | 6.63** | 2 | 83 | 0.16 | 0.25 | 2.49* | ||
| 冲突距离任务 | 0.08 | 7.31** | 2 | 83 | 0.18 | 0.29 | 2.84** | ||
| 冲突平衡任务 | 0.10 | 9.08*** | 2 | 83 | 0.22 | 0.32 | 3.25** |
本研究发现儿童会使用外部动作辅助解决天平任务，儿童主要用手指辅助数清砝码个数和砝码到支点的距离，尤以四年级(Mage =10.23岁)使用最多。手指策略体现了动作与认知加工的交互作用(Itaguchi，Yamada， & Fukuzawa，2015)。进入五年级后开始出现出声思维。出声思维有助于儿童认清自己的认知过程并及时调整策略(Bannert & Mengelkamp，2008；McKeown & Gentilucci，2007)，是元认知监控能力发展的重要表现；辅助策略类型不断内化的趋势反映了儿童思维能力的发展。
4.2 儿童解决五类天平任务的比例推理策略选择表现 4.2.1 策略选择多样性的表现各年级的策略选择既有重合又不断变化，儿童在不同任务中不断尝试新策略，且在同种任务类型下也会使用不同策略。支持了重波模型的观点(van der Maas & Jansen，2003)。随着任务难度增加，儿童所选择的策略种类也随之增加，如五年级儿童开始运用乘法策略解决冲突问题。
4.2.2 策略选择适应性的表现结合策略选择水平的发展特点与任务特点可知，首先，三个年级主要采用重量策略。他们都能采用重量或双维策略熟练地解决简单重量任务。其中，在简单任务中使用双维策略相比使用简单重量策略体现了更严密的思维能力。其次，虽然在距离任务中儿童选择距离策略的频率相对较高，且表现出了使用频次随年龄增多的趋势，但距离策略的使用率总体仍远低于重量策略。这提示了影响儿童解决天平任务的一个潜在因素可能是两个维度物理意义的可理解性不对等。
再次，三个年级均能使用定性比例推理策略，尽管使用频率不高。定性思维表明儿童在未接受正式比例教育之前，初步认识了两个维度的共变关系(Hilton，Hilton，Dole， & Goos，2013)，能朴素地认知天平的物理特性。提示教师注意学生已有的定性思维准备状态，以更有效的方法帮助学生发展比例思维。
此外，本研究还发现儿童在冲突任务上能使用“运货车策略”，尤其是六年级儿童使用该策略的频次显著增加。这说明儿童比例推理的灵活性不断发展。这种策略可能相比乘法策略更真切。有研究对乘法策略也提出了质疑(Johnson，2013)，认为儿童之所以难以理解乘法策略，是因为该策略不是自然产生的，讲授这种策略反而有碍比例推理的发生。
近期研究已开始寻找促进比例推理能力的教学方法。比如进行交叉相乘的算法训练(Van de Walle，Karp，Bay-Williams，Wray， & Rigelman，2007)，设计可以与同伴互动的积木任务(Schwarz & Linchevski，2007)，用图式指导法(Jitendra，Star，Rodriguez，Lindell， & Someki，2011)帮助儿童理解比例推理的数学问题结构等。
我们还发现儿童的错误策略有如下特点：
第一，在冲突任务中盲目使用补偿策略，认为在天平两边的砝码个数和距离不对等时，重量和距离总是相互补偿，使天平保持平衡。第二，儿童对熟悉的简单策略有依赖，使用错误的简单策略得到复杂任务的正确答案。比如，解决冲突重量任务最好的方法是乘法策略，但大多数儿童使用了简单重量策略，即仅通过重量多少判断天平倾斜方向，虽然该策略也能得到正确答案，儿童却并未理解该任务的实质(Boyer，Levine， & Huttenlocher，2008)。
另外，以往研究发现儿童在解决比例推理问题时可能将加法推理和乘法推理混淆(Artut & Pelen，2015; Van Dooren，De Bock，Vleugels， & Verschaffel，2010)。Jeong等人(2007)也发现10岁儿童会用加法判断6/10大于4/6。本研究发现儿童在解决冲突类天平任务时开始使用加法策略，将距离和重量加和。虽然该策略是错的，但儿童对两个维度进行了运算操作，仍属于水平相对较高的策略。
了解儿童错误策略的特点有助于教师认清学生的知识准备状态，提醒教师要注意帮助学生区分比例和非比例情境，帮助其辨认何时适用加法或乘法策略。此外，提示教师要引导学生思考各维度和整体比例的关系。
4.3 儿童解决五类天平任务的比例推理策略效用表现首先，冲突类任务的解题时间没有年级差异，正确率却表现出了明显差异。这说明儿童在等量的时间内正确解决较复杂的天平问题的能力随年龄不断提高。
值得注意的是，本研究发现六年级儿童解决冲突重量问题的正确率反而低于四、五年级。该题型的特点是较轻的砝码离支点较远，较重的砝码离支点较近，且天平总是偏向较重的一方。也就是说，用简单重量这个错误策略解决该类任务同样可以得到正确答案。结合冲突重量问题的策略选择结果可知，四、五年级儿童主要使用了简单重量策略，六年级儿童则尝试寻求其他多样的策略。因此，四、五年级儿童在冲突重量问题上虽表面表现出较高的正确率，实则对任务的加工深度、策略使用的灵活性仍不及六年级。此外，在完成该任务时，五年级使用乘法策略的频次(9次)多于六年级(1次)，这可能是由于虽然我们在取样时避开了各年级儿童接受比例推理教育的时间，但仍无法控制家庭、课外教育等因素的潜在影响；后续研究应注意收集儿童的数学成就得分作为协变量，以获得更严谨的研究结果。该研究结果也提醒我们在采用反应时和正确率指标作为儿童认知加工能力指标时，需谨慎解释研究结果。
需要说明的是，本研究仅从总体上讨论了策略效用的发展特点，实际上，由于天平任务的正确率受题目类型的影响，如重量策略在简单重量问题中能得到正确答案，在冲突距离问题中则得不到正确答案。理论上需要结合任务类型和策略类型以及年级特点进行多因素方差分析，才能深入挖掘具体的策略效用，但这种方法所得结果将难以解释。后续研究需要寻找更好的方法探讨比例推理策略效用的发展特点。
4.4 一般推理能力对儿童比例推理策略表现的影响首先，在策略选择方面，本研究发现在控制了年龄因素的影响后，一般推理能力对策略多样性有正向预测作用，即一般推理能力越强的儿童，会使用更多样的策略解决各类天平问题。此外，一般归纳推理能力对重量策略的使用频次有负向预测作用。这说明随着一般推理能力的提高，儿童对简单策略的依赖性降低。同时，一般归纳推理能力对距离策略和运货车策略的使用频次有正向预测作用。前文已表明距离维度比重量维度更难理解，一般推理能力强的儿童可能更容易发掘距离维度的意义，体现为距离策略的使用频次较多。运货车策略体现了儿童自发地理解天平原理。因此，一般推理能力较高的儿童其灵活使用比例推理策略的能力可能更高。
其次，在策略效用方面，本研究发现一般推理能力能正向预测儿童解决冲突类天平任务的正确次数。这提示了一般推理能力对解决较复杂的比例推理问题的作用更大，反言之，在难度较小的比例推理问题中，可能并不需要很强的一般推理能力也能完成。
4.5 研究展望首先，由于天平任务需同时表征两个维度的变量，这与守恒任务的要求相似，已有研究表明守恒能力与执行功能密切相关(Schirlin & Houdé，2007)，比例推理策略选择的适应能力增强可能也同样反映了主体执行功能的发展(Zelazo & Müller，2002)。未来可考察执行功能与比例推理的关系。其次，比例推理研究包含多种任务范式，未来可结合不同的学科特点同时选用多个任务进行多角度实验研究，还可以从数量特征的角度，比较儿童进行连续量比例推理和离散量比例推理的特点异同(Boyer，Levine， & Huttenlocher，2008)。
5 结论(1) 在接受正式比例教学之前，儿童能根据任务难度自发产生新策略，具备策略选择的多样性和适应性。其中，三个年级均能使用定性比例推理策略(双维策略，IIIA策略，补偿策略)，表明儿童初步认识了距离和重量两个维度的共变关系。此外，六年级儿童能使用“运货车策略”将冲突问题化解为简单问题，表现出比例推理思维的灵活性。
(2) 儿童的错误比例推理策略特点为：在冲突任务中盲目使用补偿策略，使用简单策略或者加法策略解决冲突任务等。
(3) 儿童在等量的时间内正确解决比例推理的能力随年级不断提高，但由于在某些情况下(如冲突重量任务)使用错误策略也会得到正确答案，造成解题效率高的假象，需注意谨慎使用正确率和反应时解释儿童的解题效率。
(4) 控制年龄后，儿童的一般推理能力越高，其对重量策略的依赖性越低，且可能更容易发掘距离维度的意义，其灵活使用运货车策略的能力可能更高。此外，一般推理能力对解决较复杂的比例推理问题的作用可能更大。
参考文献
| Adjiage R, & Pluvinage F (2007). An experiment in teaching ratio and proportion. Educational Studies in Mathematics , 65(2), 149-175. DOI: 10.1007/s10649-006-9049-x. |
| Akatugba A.H, & Wallace J (2009). An integrative perspective on students' proportional reasoning in high school physics in a West African context. International Journal of Science Education , 31(11), 1473-1493. DOI: 10.1080/09500690802101968. |
| Artut P.D, & Pelen M.S (2015). Sixth grade students' solution strategies on proportional reasoning problems. Procedia-Social and Behavioral Sciences , 197, 113-119. DOI: 10.1016/j.sbspro.2015.07.066. |
| Bannert M, & Mengelkamp C (2008). Assessment of metacognitive skills by means of instruction to think aloud and reflect when prompted. Does the verbalization method affect learning? Metacognition and Learning , 3(1), 39-58. |
| Boom J, & Hoijtink H (2001). Rules in the balance. Cognitive Development , 16, 717-735. DOI: 10.1016/S0885-2014(01)00056-9. |
| Boyer T.W, Levine S.C, & Huttenlocher J (2008). Development of proportional reasoning: Where young children go wrong. Developmental Psychology , 44(5), 1478-1490. DOI: 10.1037/a0013110. |
| Coyle T.R, & Bjorklund D.F (1996). The development of strategic memory: A modified microgenetic assessment of utilization deficiencies. Cognitive Development , 11(2), 295-314. DOI: 10.1016/S0885-2014(96)90006-4. |
| Cramer K, & Post T (1993). Proportional reasoning. The mathematics teacher , 86(5), 404-407. |
| Dandurand F, & Shultz T.R (2014). A comprehensive model of development on the balance-scale task. Cognitive Systems Research , 31-32-1-25. |
| Gignac G.E (2015). Raven's is not a pure measure of general intelligence: Implications for g factor theory and the brief measurement of g. Intelligence , 52, 71-79. DOI: 10.1016/j.intell.2015.07.006. |
| Heller P.M, Post T.R, Behr M, & Lesh R (1990). Qualitative and numerical reasoning about fractions and rates by seventh-and eighth-grade students. Journal for Research in Mathematics Education , 21, 388-402. DOI: 10.2307/749396. |
| Hilton A, Hilton G, Dole S, & Goos M (2013). Development and application of a two-tier diagnostic instrument to assess middle-years students' proportional reasoning. Mathematics Education Research Journal , 25(4), 523-545. DOI: 10.1007/s13394-013-0083-6. |
| Itaguchi Y, Yamada C, & Fukuzawa K (2015). Writing in the air: Contributions of finger movement to cognitive processing. PLoS ONE , 10(6), 1-17. |
| Jansen B.R. J, & van der Maas H.L. J (2002). The development of children's rule use on the balance scale task. Journal of Experimental Child Psychology , 81(4), 383-416. DOI: 10.1006/jecp.2002.2664. |
| Jeong Y, Levine S.C, & Huttenlocher J (2007). The development of proportional reasoning: Effect of continuous versus discrete quantities. Journal of Cognition and Development , 8(2), 237-256. DOI: 10.1080/15248370701202471. |
| Jitendra A.K, Star J.R, Dupuis D.N, & Rodriguez M.C (2013). Effectiveness of schema-based instruction for improving seventh-grade students' proportional reasoning: A randomized experiment. Journal of Research on Educational Effectiveness , 6(2), 114-136. DOI: 10.1080/19345747.2012.725804. |
| Jitendra A.K, Star J.R, Rodriguez M, Lindell M, & Someki F (2011). Improving students' proportional thinking using schema-based instruction. Learning and Instruction , 21(6), 731-745. DOI: 10.1016/j.learninstruc.2011.04.002. |
| Johnson, K. H. 2013. Understanding proportional reasoning in pre-service teachers (Order No. 3576466). Available from ProQuest Dissertations and Theses A & I: The Humanities and Social Sciences Collection. (1477235539). Retrieved from http://search.proquest.com/docview/1477235539?accountid=8554 |
| Karplus E.F, Karplus R, & Wollman W (1974). Intellectual development beyond elementary school IV: Ratio, the influence of cognitive style. School Science and Mathematics , 74(6), 476-482. DOI: 10.1111/ssm.1974.74.issue-6. |
| McKeown R.G, & Gentilucci J.L (2007). Think-aloud strategy: Metacognitive development and monitoring comprehension in the middle school second-language classroom. Journal of Adolescent & Adult Literacy , 51(2), 136-147. |
| Noelting G (1980). The development of proportional reasoning and the ratio concept Part I-Differentiation of stages. Educational studies in mathematics , 11(2), 217-253. DOI: 10.1007/BF00304357. |
| Normandeau S, Larivée S, Roulin J, & Longeot F (1989). The balance-scale dilemma: Either the subject or the experimenter muddles through. The Journal of Genetic Psychology , 150(3), 237-250. DOI: 10.1080/00221325.1989.9914594. |
| Quinlan P.T, Van D.M. H. L, Jansen B.R.J, Booij O, & Rendell M (2007). Re-thinking stages of cognitive development: An appraisal of connectionist models of the balance scale task. Cognition , 103(3), 413-459. DOI: 10.1016/j.cognition.2006.02.004. |
| Schirlin O, & Houdé O (2007). Negative priming effect after inhibition of weight/number interference in a Piaget-like task. Cognitive Development , 22(1), 124-129. DOI: 10.1016/j.cogdev.2006.06.003. |
| Schwarz B.B, & Linchevski L (2007). The role of task design and argumentation in cognitive development during peer interaction: The case of proportional reasoning. Learning and Instruction , 17(5), 510-531. DOI: 10.1016/j.learninstruc.2007.09.009. |
| Siegler R.S (1976). Three aspects of cognitive development. Cognitive Psychology (4), 481-520. |
| Siegler R.S (1999). Strategic development. Trends in Cognitive Sciences , 3(11), 430-435. DOI: 10.1016/S1364-6613(99)01372-8. |
| Siegler R, & Jenkins E.A (2014). . How children discover new strategies (2th Edition) , 6, 27. |
| Van de Walle J.A, Karp K.S, Bay-Williams J.M, Wray J.A, & Rigelman N.R. M (2007). Elementary and middle school mathematics: Teaching developmentally. MA: America: Pearson Publication : 115 -133. |
| Van der Maas H.L, & Jansen B.R (2003). What response times tell of children's behavior on the balance scale task. Journal of Experimental Child Psychology , 85(2), 141-177. DOI: 10.1016/S0022-0965(03)00058-4. |
| Van Dooren W, De Bock D, Vleugels K, & Verschaffel L (2010). Just answering … or thinking? Contrasting pupils' solutions and classifications of missing-value word problems. Mathematical Thinking & Learning , 12(1), 20-35. |
| Zelazo P.D, & Müller U (2002). The balance beam in the balance: Reflections on rules, relational complexity, and developmental processes. Journal of Experimental Child Psychology , 81(4), 458-465. DOI: 10.1006/jecp.2002.2667. |
| 刘电芝, 杨会会. (2008). 几种策略选择模型的发展轨迹与比较. 心理科学 , 31(1), 156-159. |
| 张厚粲, 王晓平. (1989). 瑞文标准推理测验在我国的修订. 心理学报 (02), 113-121. |