国家教育部主管、北京师范大学主办。
文章信息
- 牛玉柏, 时冉冉, 曹贤才. 2016.
- NIU Yubai, SHI Ranran, CAO Xiancai. 2016.
- 学前儿童近似数量系统敏锐度与符号数学能力的关系
- Preschool Children's Approximate Number System Acuity and Symbolic Number Abilities
- 心理发展与教育, 32(2): 129-138
- Acta Meteorologica Sinica, 32(2): 129-138.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2016.02.01
2. 北京师范大学发展心理研究所, 北京 100875
2. Institute of Developmental Psychology, Beijing Normal University, Beijing 100875
数量表征的研究表明,我们对物体或事件数量的表征依赖于两种不同的表征系统,即精确的表征系统和近似的表征系统(王乃弋,罗跃嘉,李红,2006)。其中成人、婴儿和动物共有近似的表征系统,被称为近似数量系统(approximate number system, ANS)(Halberda & Feigenson, 2008),而它们是否具有精确表征系统尚存在争议(王乃弋等,2006)。ANS是通过“心理数字线”(mental number line)的连续激活对数量进行表征的,具有噪音和不精确性,可以通过相互重叠的正态分布来模拟(如图 1)(Pica, Lemer, Izard, & Dehaene, 2004)。同时,它对数量的表征遵从韦伯定律,即对数量的区分依赖于数量的比率,因此韦伯系数常作为个体ANS敏锐度的指标(Halberda, Mazzocco, & Feigenson, 2008)。ANS对数量的表征是跨通道的,对视觉数量和听觉刺激数量的表征均存在这种近似的方式(Barth, La Mont, Lipton, & Spelke, 2005)。脑研究也表明其存在相应的脑区定位,位于双侧顶内沟(bilateral intraparietal sulcus, IPS)处(Cantlon, Platt, & Brannon, 2009)。对ANS的研究对于明确人类数学能力从何而来具有重要的意义。
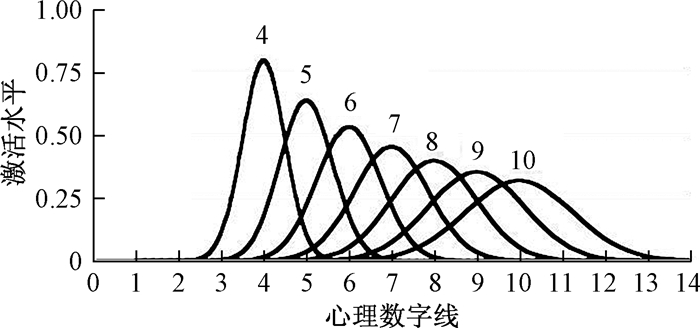 |
| 图 1 近似数量系统对数量的表征形式 |
近年来,越来越多的研究开始探讨ANS与数学能力间的关系。首先,Halberda等人(2008)的纵向研究发现,在控制众多非数量的一般认知能力后,14岁被试的韦伯系数与其学前阶段的数学能力测验(Test of Early Math Ability, TEMA)及小学各年级的数学能力测验(Woodcock-Johnson revised calculation subtest, WJ-Rcalc)总分都显著相关。随后,在其他年龄阶段被试及计算障碍被试群体中均发现了二者间显著的正相关关系,且不因ANS敏锐度的指标不同而不同(Halberda, Ly, Wilmer, Naiman, & Germine, 2012; Mazzocco, Feigenson, & Halberda, 2011a)。由此,研究者们认为,ANS可能是我们获得数概念及发展更为高级的数学能力的基础,对二者关系的研究可以用来解释、预测数学能力的个体差异,为数学学习困难儿童的干预提供新的思路。
已有研究较多采用点数比较任务来测量被试的ANS敏锐度,该任务要求被试判断两个阵列的点数谁更多。此外,采用点数异同任务的结果同样符合数量表征的假设,表现出距离效应,但与点数比较任务相比,该范式中被试无法依据数量的序数位置来进行判断(van Opstal & Verguts, 2011)。此外,刺激的非数量特征在两种任务中的作用不同。Gebuis和van der Smagt(2011)认为,与点数比较任务相比,成人被试在点数异同任务中更少依赖点的非数量信息(如总面积、周长等)来进行数量多少的判断,因此点数异同任务测得的数表征敏锐度会更纯净。然而,幼儿被试的研究却发现,刺激的非数量信息(如大小、形状、颜色等)会阻碍点数异同任务中对数量信息的提取而不会影响非符号比较任务(Cantlon, Fink, Safford, & Brannon, 2007)。这些差异均表明,点数比较任务要难于点数异同任务。但也可发现,无论哪种任务,均可能受非数量信息的影响。虽然两种任务均可用于ANS敏锐度的测量,但已有研究中多采用点数比较任务来考察ANS敏锐度与符号数学能力的关系。如果ANS是发展符号数学能力的基础,那么这种显著的相关关系不会因为任务改变而变化。因此本研究同时采用两种任务来考察二者关系的稳定性,根据前面的分析本研究假设,学前儿童在点数异同任务上的表现要差于点数比较任务,但两种任务与符号数学能力均显著相关。
在数认知研究中,符号数学能力特指与数字符号(阿拉伯数字或文字)有关的数学认知能力,为人类特有(Park & Brannon, 2013)。学前阶段与正式入学后的符号数学能力存在差异,幼儿通过数学有关的游戏、与老师父母间与数量有关的对话等经验获得对数字符号意义及关系的理解(Klibanoff, Levine, Huttenlocher, Vasilyeva, & Hedges, 2006)。学前儿童的符号数学能力是一个多维度的结构,包含唱数、基数、计数、简易计算等内容(Ginsburg, & Baroody, 1990),表现出较大的个体差异,并能正向预测个体在小学时期的数学成就和数学成就的增长速度(Jordan, Kaplan, Ramineni, & Locuniak, 2009)。那么ANS敏锐度与符号数学能力不同维度间的关系是否不同?Lourenco, Bonny, Fernandez和Rao(2012)发现,点数比较任务成绩与计算测验(WJ-caculation)显著相关而与几何测验不相关。从这些研究可以看到,学前儿童ANS敏锐度与符号数学能力不同维度间的关系可能不同。Libertus, Feigenson和Halberda(2013a)发现学前儿童点数比较任务的正确率与TEMA测验中正式数学能力维度分数无关而与非正式数学能力维度分数显著相关。他们认为ANS对于数值定位系统(place value system)的理解和回忆基本的数字事实的作用并不明显。然而该研究并没有进行更为细致的划分。按照正式数学能力与非正式数学能力包含的范畴,本研究假设,学前儿童的ANS与数数、基数和符号数字知识均显著相关,与简易计算成绩无显著相关。
ANS敏锐度与符号数学能力关系的研究中,研究者控制了工作记忆、言语能力分数后仍能发现二者间显著的相关关系(Halberda et al., 2012; Halberda et al., 2008; Libertus, Feigenson, & Halberda, 2011)。近年来有学者认为,ANS敏锐度与数学能力间的关系可能受抑制控制的影响。在点数比较任务中,为了排除点的非数量信息(以总面积为例)对被试进行数量判断的影响,存在两种条件,一种条件下点数多的阵列总面积大,一种条件下点数少的阵列总面积大。在条件二中,被试需要抑制总面积信息来进行数量多少的判断,类似于stroop任务,如果被试的抑制控制能力更好,则总的正确率会更高,因此点数比较任务的成绩很可能反映了被试的抑制控制能力(Fuhs & McNeil, 2013; Gilmore et al., 2013)。但也有研究表明抑制控制并不影响二者间的相关关系(Halberda et al., 2008)。然而在以学前儿童为被试的研究中很少控制抑制控制的作用,因此,本研究在控制工作记忆和言语能力分数的同时,也控制了抑制控制的分数。
综上,本研究在控制学前儿童的抑制控制、言语等多种一般认知能力后,考察同时采用了点数比较任务和点数异同任务测得的ANS敏锐度与符号数学能力多种成分间的相互关系。
2 研究方法2.1 被试采用方便取样,选取杭州市某幼儿园3~6岁幼儿122名(女孩60名),年龄范围为39~78月(M=59月,SD=12月),其中,3、4、5、6岁幼儿分别为31名、30名、35名、26名。
2.2 实验材料2.2.1 ANS敏锐度测验(1)点数比较任务
参考Halberda等人(2008)的研究,要求幼儿判断呈现在电脑屏幕上相互分离的蓝色和黄色的点哪种颜色的点更多。该测试包含6个练习试次和60个实验试次,每个试次呈现时间为1200ms。每种颜色的点数量范围为5~21,两种颜色点的数量比率有五种,分别为1:2、2:3、3:4、6:7、7:8。为了平衡其他无关因素,一半试次黄色的点更多,一半蓝色的点更多;一半试次两阵列点的平均面积相等,一半点的总面积相等。每个点的大小默认为36±20%像素。幼儿口头回答后由主试按键,记录被试判断的正确率。
(2)点数异同任务
参考Gebuis和van der Smagt(2011)的研究,要求幼儿判断两种颜色点的数目是否一样多。该测试也包括6个练习和60个实验试次,每种颜色点数范围为5~21,一半试次点数目相同,一半试次点数目不同,比例分别是1:2、2:3、3:4、6:7、7:8。其他平衡方法及结果记录同点数比较任务。
2.2.2 符号数学能力测验采用Mussolin, Nys和Leybaert(2012)研究中的三个测验,并增加了简易加减测验。(1)数数测验。考察幼儿的数数能力,要求幼儿从“1”数到“60”,能数到的最高值作为该测验的分数。(2)基数测验。只考察3~4岁幼儿的基数能力,要求幼儿从水果形状的橡皮中选出x个(其中x从1、2、3、4、5、7中随机选择),共12个试次,最高分12分。(3)符号数字系列测验。内容包括:幼儿对数字序列的掌握;对阿拉伯数字知识的掌握;快速给出数目的能力;数字单词的识别;数量多少的判断能力。考察幼儿符号数字知识的掌握情况,共61个试次,最高分63分。(4)简易加减法。考察幼儿的简单计算能力,内容为10以内的加减法,包含加减各10个试次,测验最高分为20分。
2.2.3 数字记忆广度测验采用麦卡锡幼儿智能量表中的“数字记忆”分测验。主试间隔1秒读出数字,幼儿按顺序和逆序复述,得分为连续两次正确按顺序、逆序复述的数列长度,最高分别为8分和5分,分别作为短时记忆和工作记忆的成绩。
2.2.4 皮博迪图片词汇测验(PPVT)该测验由Llody Dunn及Leota Dunn编制,桑标等人1990进行了修订,通过测验儿童的听觉词汇能力反映其语言能力和一般智力状况。要求幼儿在4张图片中选择出听到的词汇意思相同的那幅图,共175个词汇,若连续8张中有6张反应错误就停止,对1题记1分。
2.2.5 抑制控制能力测试因采用多个抑制控制任务比一个任务更可靠(Fuhs & McNeil, 2013),选用如下测试:
(1)白天/黑夜任务
由Gerstadt, Hong和Diamond(1994)设计。在确认幼儿认识图片上的太阳和月亮,且能把太阳(月亮)与白天(黑天)联系在一起,要求幼儿看到“太阳”图片时报告“黑夜”;当看到“月亮”图片时报告“白天”。随机呈现太阳和月亮图片各12张,对1题记1分。
(2)木棒敲击任务
最先由Luria开发用来研究有额叶损伤的成人,并且被Diamond和Taylor(1996)运用于儿童。要求当主试用木棒敲击1次后,幼儿立即用木棒敲击两次;主试敲击两次,幼儿立即敲击1次。共进行16次,敲击正确则记1分。
2.3 实验设计和程序采用被试内设计。实验在幼儿熟悉的房间单独施测。所有测验项目分两次进行,每次时间约为三十分钟,两次时间间隔不超过一周。因图片词汇测验及数学能力测验时间较长,且部分任务具有相似性,所以为平衡测验顺序及控制每次测验的时间,采用四种测验顺序,顺序1:第一天进行点数比较任务、数字顺序播报、白天/黑夜和符号数学能力测验,第二天测试其他任务;顺序2:第一天进行点数异同任务、数字顺序播报、白天/黑夜任务和符号数学能力测验,第二天测试其他任务;顺序3:先进行顺序1第二天任务;顺序4:先进行顺序2第二天任务。首先采用拉丁方方法把被试安排到这四个顺序中,再采用拉丁方顺序给被试安排当天要完成的四个任务。
3 研究结果3.1 各变量的描述性统计因被试不愿参与、不理解指导语或其他非实验原因,并非所有的被试都完成了全部测验任务,此外,基数测验只适用于3~4岁被试。各变量完成测验的人数及描述性统计结果如表 1所示。
| 变量 | n | 极小值 | 极大值 | M | SD |
| ANS敏锐度 | |||||
| 点数比较正确率 | 120 | 41.67% | 88.33% | 66.86% | 11.47% |
| 点数异同正确率 | 112 | 36.67% | 71.67% | 54.93% | 7.01% |
| 符号数学能力系列测验 | |||||
| 数数 | 122 | 1 | 60 | 36.08 | 21.22 |
| 基数 | 61 | 0 | 12 | 7.41 | 3.25 |
| 符号数字知识测验 | 121 | 17 | 63 | 45.93 | 13.56 |
| 简易加减法 | 121 | 0 | 20 | 8.17 | 8.27 |
| 数字记忆广度测试 | |||||
| 短时记忆 | 122 | 1 | 8 | 4.70 | 1.30 |
| 工作记忆 | 118 | 1 | 5 | 1.93 | 1.04 |
| 抑制控制测试 | |||||
| 白天/黑夜 | 121 | 0 | 24 | 17.55 | 6.69 |
| 木棒敲击 | 121 | 0 | 16 | 12.39 | 3.62 |
| 皮博迪图片词汇测验 | 122 | 7 | 106 | 41.67 | 25.90 |
(1)以正确率为指标
各年龄组被试的描述性统计结果如表 2所示。各年龄组成绩的正确率均大于随机水平(p<0.01)。以年龄和比率为自变量,点数比较任务的正确率为因变量进行混合设计方差分析。结果发现,年龄的主效应显著,F(3,116)=17.037,p<0.01,η2=0.31,除5岁组和6岁组被试的成绩差异不显著外,其他年龄组间的成绩两两比较均差异显著(p<0.05)。这表明,随着年龄增长,幼儿在点数比较任务上的表现越好。比率的主效应显著,F(4,464)=50.657,p<0.01,η2=0.30,除比率为1:2与2:3时被试成绩差异不显著及2:3与3:4差异边缘显著外(p<0.1),其他比率条件间的成绩比较均表现为比率越接近1,被试判断的正确率越低(p<0.05)。年龄与比率的交互作用不显著,表明各年龄组被试在点数比较任务上的成绩随比率改变其变化趋势一致。
| 点数比率 | 3岁组(n=31) | 4岁组(n=30) | 5岁组(n=33) | 6岁组(n=26) | 总计(N=120) |
| 1:2 | 65.86±19.88 | 72.78±19.20 | 81.31±18.98 | 87.50±13.79 | 76.53±19.80 |
| 2:3 | 63.71±15.45 | 68.06±16.96 | 77.02±19.21 | 83.65±15.72 | 72.78±18.42 |
| 3:4 | 59.14±11.46 | 65.56±16.91 | 73.23±13.62 | 76.60±16.33 | 68.40±15.95 |
| 6:7 | 53.49±12.69 | 60.83±14.54 | 65.15±14.05 | 67.95±13.06 | 61.67±14.51 |
| 7:8 | 49.19±11.66 | 52.78±13.90 | 60.10±12.80 | 57.69±14.13 | 54.93±13.64 |
(2)以韦伯系数为指标
采用心理物理学模型对被试的韦伯系数进行估计。该模型假设,两个阵列的点数分别为n1和n2时,各自的心理表征符合平均数为n1和n2,标准差为韦伯系数与平均数乘积的正态分布,点数之差同样为正态分布,平均数为n1-n2,标准差为w 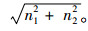 。则被试判断的正确率为正态曲线下大于0的总面积,为
。则被试判断的正确率为正态曲线下大于0的总面积,为 ,其中r为n2/n1(Pica et al., 2004)。在该任务中,每个被试在各比率下均存在一个正确率,通过L-M算法可以获得自由参数w, 也即韦伯系数。
,其中r为n2/n1(Pica et al., 2004)。在该任务中,每个被试在各比率下均存在一个正确率,通过L-M算法可以获得自由参数w, 也即韦伯系数。
删除不能拟合模型和3个标准差外的数据,剩余101名被试的描述性统计结果如表 3所示。方差分析发现,年龄效应显著,F(3,97)=4.263,p<0.01,η2=0.12,6岁组被试的韦伯系数显著小于3岁组和4岁组(p<0.05),5岁组与3岁组差异边缘显著(p<0.1),其他组别间差异不显著。表明随着年龄增长,ANS敏锐度越好。
| 3岁组 | 4岁组 | 5岁组 | 6岁组 | 总计 | |
| n | 20 | 24 | 32 | 25 | 101 |
| M | 0.78 | 0.73 | 0.55 | 0.35 | 0.59 |
| SD | 0.44 | 0.56 | 0.53 | 0.21 | 0.48 |
(1)以总正确率为指标
各年龄组被试点数异同任务描述性统计结果如表 4所示,各年龄组成绩的正确率均大于随机水平(p<0.01)。方差分析发现,年龄效应显著,F(3,108)=3.513,p<0.05,η2=0.09,6岁组被试的正确率显著高于3岁组(p<0.05),6岁组与4岁组、6岁组与5岁组、5岁组与3岁组差异边缘显著(p<0.1),其他年龄组间差异均不显著。这表明随着年龄增长,幼儿在点数异同任务中的表现越好。
| 3岁组 | 4岁组 | 5岁组 | 6岁组 | 总数 | |
| n | 27 | 27 | 34 | 24 | 112 |
| M | 52.04 | 54.69 | 55.10 | 58.19 | 54.93 |
| SD | 4.86 | 5.76 | 8.49 | 6.95 | 7.01 |
(2)以点数不同试次正确率为指标
除总正确率外,研究者还采用点数不同试次的正确率作为ANS敏锐度的指标(van Opstal & Verguts, 2011)。在排除测验中存在明显反应偏好的被试数据(倾向于回答“一样多”或“不一样多”)后共有90名被试。这些被试与排除的被试在年龄、数学能力、记忆广度、抑制控制和词汇能力测验分数上均无显著差异(p>0.05)。描述性统计结果如表 5所示。各年龄组成绩的正确率均显著大于随机水平(p<0.01)。
| 点数比率 | 3岁组(n=20) | 4岁组(n=22) | 5岁组(n=28) | 6岁组(n=20) | 总计(N=90) |
| 1:2 | 49.17±30.34 | 52.27±26.87 | 69.05±26.34 | 74.17±21.27 | 61.67±27.98 |
| 2:3 | 47.50±27.72 | 59.09±31.59 | 63.10±25.40 | 69.17±22.47 | 60.00±27.57 |
| 3:4 | 40.00±25.59 | 48.48±21.77 | 51.79±23.28 | 66.67±29.62 | 51.67±26.21 |
| 6:7 | 45.00±26.55 | 48.49±24.07 | 55.36±17.60 | 56.67±21.90 | 51.67±22.49 |
| 7:8 | 48.33±28.05 | 49.24±21.50 | 54.17±24.69 | 64.17±20.43 | 53.89±24.23 |
以年龄和比率为自变量,被试在点数不同试次上的正确率为因变量进行混合设计方差分析发现,年龄的主效应显著,F(3,86)=5.053,p<0.01,η2=0.15,6岁组成绩显著高于3岁组和4岁组(p<0.05),5岁组显著高于3岁组(p<0.05),其他年龄组间差异不显著。这表明,随着年龄增长,幼儿的ANS敏锐度逐渐提高。比率的主效应显著,F(4,344)=4.693,p<0.01,η2=0.05,点数比率为1:2正确率显著高于2:3和3:4时的正确率(p<0.05),2:3与6:7时正确率差异边缘显著(p<0.1),其他比率间的正确率差异均不显著。这表明,点的比率越接近1,被试判断的正确率越低。年龄与比率的交互作用不显著,表明各年龄组被试的成绩随比率改变其变化趋势一致。
3.2.3 两种任务难度的比较各年龄及任务类型条件下被试判断的正确率如图 2所示。以年龄和任务类型为自变量,正确率为因变量进行方差分析发现,任务类型的主效应显著,F(1,106)=135.776,p<0.001,η2=0.56,即点数比较任务的成绩显著高于点数异同任务。交互效应显著,F(3,106)=6.157,p<0.05,η2=0.15,简单效应分析表明,各年龄组内点数比较任务正确率均显著高于点数异同任务(p<0.001)。
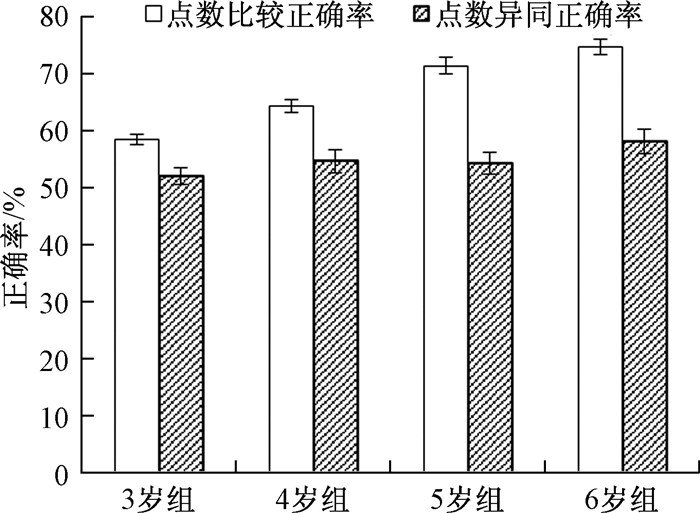 |
| 图 2 各年龄组学前儿童在两种任务类型下的正确率 |
对各变量两两间进行Pearson相关分析,结果见表 6所示。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 DCA | ||||||||||||
| 2 WF | -0.76** | |||||||||||
| 3 SDA | 0.26** | -0.08 | ||||||||||
| 4 SDNA | 0.30** | -0.24* | 0.55** | |||||||||
| 5 PPVT | 0.51** | -0.35** | 0.34** | 0.32** | ||||||||
| 6 短时记忆 | 0.35** | -0.13 | 0.27** | 0.26* | 0.43** | |||||||
| 7 工作记忆 | 0.48** | -0.37** | 0.27** | 0.20 | 0.59** | 0.45** | ||||||
| 8 白天/黑夜 | 0.39** | -0.25* | 0.22* | 0.07 | 0.40** | 0.42** | 0.45** | |||||
| 9 木棒敲击 | 0.48** | -0.31** | 0.31** | 0.07 | 0.53** | 0.39** | 0.49** | 0.59** | ||||
| 10 数数 | 0.52** | -0.35** | 0.30** | 0.31** | 0.60** | 0.49** | 0.63** | 0.53** | 0.61** | |||
| 11 基数 | 0.39** | -0.23 | 0.24 | 0.08 | 0.28* | 0.37** | 0.25 | 0.38** | 0.64** | 0.51** | ||
| 12 数字知识 | 0.60** | -0.40** | 0.32** | 0.35** | 0.67** | 0.60** | 0.60** | 0.61** | 0.69** | 0.79** | 0.66** | |
| 13 简易加减 | 0.51** | -0.37** | 0.26** | 0.31** | 0.66** | 0.52** | 0.65** | 0.50** | 0.52** | 0.72** | 0.30* | 0.78** |
| 注:DCA=点数比较任务正确率,WF=韦伯系数,SDA=点数异同任务正确率,SDNA=点数不同试次正确率。 **.在 0.01 水平(双侧)上显著。*.在 0.05 水平(双侧)上显著。以下同。 |
||||||||||||
结果表明,除韦伯系数与点数异同任务正确率相关不显著外,ANS敏锐度各指标间均显著相关;除基数能力外,ANS敏锐度各指标与其他符号数学能力均显著相关。
3.4 ANS敏锐度对符号数学能力的预测作用为分析ANS敏锐度各指标对符号数学能力各维度的预测作用,进行分层回归分析。第一层放入控制变量,有PPVT、短时记忆、工作记忆及抑制控制测验的分数;第二层放入预测变量,为ANS敏锐度的各个指标。因变量为符号数学能力的各维度。点数比较任务下的结果如表 7和表 8所示。
| 项目 | 变量 | 数数 | 基数 | 符号数字知识 | 简易加减 | ||||
| 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | ||
| PPVT | 0.19* | 0.15+ | 0.04 | -0.03 | 0.27** | 0.22** | 0.32** | 0.29** | |
| 短时记忆 | 0.12 | 0.11 | 0.25* | 0.23* | 0.25** | 0.24** | 0.17* | 0.16* | |
| 第一步 | 工作记忆 | 0.28** | 0.26** | -0.08 | -0.08 | 0.12 | 0.08 | 0.29** | 0.27* |
| 白天黑夜 | 0.12 | 0.11 | 0.04 | 0.02 | 0.19* | 0.17* | 0.13 | 0.12 | |
| 木棒敲击 | 0.25** | 0.22* | 0.57** | 0.56** | 0.28** | 0.24** | 0.06 | 0.03 | |
| 第二步 | 正确率 | 0.14+ | 0.23* | 0.20** | 0.12 | ||||
| F值 | 26.80** | 23.20** | 9.40** | 9.02** | 49.95** | 46.47** | 28.88** | 24.81** | |
| R2 | 0.55** | 0.56+ | 0.47** | 0.51* | 0.65** | 0.72** | 0.57** | 0.58 | |
| ΔR2 | 0.55** | 0.01+ | 0.47** | 0.04* | 0.65** | 0.03** | 0.57** | 0.01 | |
| 注:+. 在 0.1水平(双侧)上显著,以下同。 | |||||||||
| 项目 | 变量 | 数数 | 基数 | 符号数字知识 | 简易加减 | ||||
| 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | ||
| PPVT | 0.17+ | 0.15 | 0.04 | 0.01 | 0.24** | 0.22** | 0.27** | 0.26** | |
| 短时记忆 | 0.10 | 0.11 | 0.29* | 0.35** | 0.21** | 0.22** | 0.16* | 0.17* | |
| 第一步 | 工作记忆 | 0.31** | 0.29** | -0.02 | -0.11 | 0.14+ | 0.11 | 0.34*** | 0.32** |
| 白天黑夜 | 0.14 | 0.13 | 0.22 | 0.20 | 0.23** | 0.23** | 0.15+ | 0.15 | |
| 木棒敲击 | 0.21* | 0.20+ | 0.41** | 0.44** | 0.27** | 0.26** | 0.04 | 0.04 | |
| 第二步 | 韦伯系数 | -0.09 | -0.25* | -0.11+ | -0.09 | ||||
| F值 | 21.01** | 17.79** | 7.79** | 7.89** | 44.93** | 38.90** | 26.05** | 22.01** | |
| R2 | 0.52** | 0.53 | 0.48** | 0.54* | 0.70** | 0.71+ | 0.57** | 0.58 | |
| ΔR2 | 0.52** | 0.01 | 0.48** | 0.06* | 0.70** | 0.01+ | 0.57** | 0.01 | |
以上结果显示,在点数比较任务下,控制了被试的言语能力、短时记忆、工作记忆及抑制控制后,正确率能显著预测被试的基数能力和符号数字知识,韦伯系数能显著预测被试的基数能力。采用相同的方法分析了点数异同任务下各指标与符号数学能力的预测作用,结果如表 9和表 10所示。
| 项目 | 变量 | 数数 | 基数 | 符号数字知识 | 简易加减 | ||||
| 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | ||
| PPVT | 0.20* | 0.20* | 0.03 | 0.04 | 0.24 | 0.24 | 0.30** | 0.30** | |
| 短时记忆 | 0.17* | 0.17* | 0.29* | 0.30* | 0.29 | 0.29 | 0.18* | 0.18* | |
| 第一步 | 工作记忆 | 0.24** | 0.24** | -0.12 | -0.14 | 0.10 | 0.10 | 0.30** | 0.30** |
| 白天黑夜 | 0.12 | 0.12 | 0.04 | 0.04 | 0.18 | 0.18 | 0.14+ | 0.14+ | |
| 木棒敲击 | 0.26** | 0.26** | 0.63** | 0.66** | 0.30 | 0.30 | 0.06 | 0.06 | |
| 第二步 | 总正确率 | 0.01 | -0.08 | 0.00 | -0.05 | ||||
| F值 | 28.28** | 23.34** | 10.39** | 8.66** | 48.11** | 39.71** | 27.12** | 22.54** | |
| R2 | 0.58** | 0.58 | 0.525** | 0.53 | 0.70** | 0.70 | 0.568** | 0.57 | |
| ΔR2 | 0.58** | 0 | 0.525** | 0.005 | 0.70** | 0 | 0.568** | 0.002 | |
| 项目 | 变量 | 数数 | 基数 | 符号数字知识 | 简易加减 | ||||
| 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | 第一步 | 第二步 | ||
| PPVT | 0.22* | 0.19+ | 0.02 | 0.01 | 0.23** | 0.18* | 0.29** | 0.26* | |
| 短时记忆 | 0.15 | 0.13 | 0.26+ | 0.25 | 0.35** | 0.32*** | 0.14 | 0.13 | |
| 第一步 | 工作记忆 | 0.26* | 0.25* | -0.13 | -0.12 | 0.12 | 0.11 | 0.35** | 0.35** |
| 白天黑夜 | 0.15 | 0.16 | 0.11 | 0.12 | 0.21* | 0.22** | 0.13 | 0.14 | |
| 木棒敲击 | 0.15 | 0.17 | 0.51** | 0.52** | 0.17* | 0.20* | 0.00 | 0.02 | |
| 第二步 | 不同正确率 | 0.12 | 0.09 | 0.17** | 0.12 | ||||
| F值 | 16.79** | 14.54** | 5.51** | 4.60** | 35.00** | 32.71** | 19.40** | 16.75** | |
| R2 | 0.51** | 0.52 | 0.44** | 0.45 | 0.68** | 0.71** | 0.55** | 0.56 | |
| ΔR2 | 0.51** | 0.01 | 0.44** | 0.01 | 0.68** | 0.03** | 0.55** | 0.01 | |
以上结果可知,点数异同任务下,在控制了被试的言语能力、短时记忆、工作记忆及抑制控制后,总正确率不能显著预测符号数学能力各维度的分数,点数不同试次的正确率能显著预测被试的符号数字知识。
4 讨论4.1 3~6岁学前儿童ANS敏锐度的发展采用两种任务测量学前儿童ANS敏锐度的结果发现,被试判断的正确率均大于随机水平,表明两种任务下被试是基于点的数量信息作出的判断。两个阵列点数的比率越接近1,幼儿判断的正确率越低,且变化趋势不受年龄影响,这与以往点数比较任务的研究结果相同(Halberda & Feigenson, 2008)。这反映了学前儿童的数量区分能力对数量比率的依赖,支持了韦伯定律适用于描述学前儿童数量区分能力的假定,也肯定了数字距离效应的存在,符合数量表征的假设。表明两种任务均适合学前儿童ANS敏锐度的测量。
研究结果也表明了3~6幼儿的ANS敏锐度会随着年龄的增长而不断提高。正如Halberda和Feigenson(2008)发现,3~6岁幼儿及成人分别能正确区分数量的比率为2:3、3:4、4:5、6:7和9:10。在年龄差异上,虽然各指标间存在差异,但多数指标显示了较为一致的结果:5~6岁幼儿的敏锐度要显著高于3~4岁幼儿,5岁与6岁幼儿、3岁与4岁幼儿间的差异均不显著。即3~4岁及5~6岁期间,学前儿童的ANS敏锐度的发展较为缓慢,而4~5岁期间的发展较为迅速。
成熟和环境都是影响ANS敏锐度的因素。Pica等人(2004)就发现了接触过数学教育的法国成人和缺少数学经验的亚马逊原住民都具有很好的数量区分能力,但前者的韦伯系数要小于后者,这表明除成熟的影响外,数学有关的经验能够影响ANS的敏锐度。训练研究也表明反馈与训练能提高点数比较任务下的韦伯系数(Dewind & Brannon, 2012;Park & Brannon, 2013)。因此,ANS敏锐度发展的速度可能与学前儿童符号数字知识的学习有关。幼儿4岁左右时开始学习数字符号、数数、数的相对大小等知识,逐渐获得数字符号与数量的相互联系,对数量的表征越来越离散,促进了ANS敏锐度的发展;而一旦幼儿掌握了数字符号的意义后,这种促进作用减弱,ANS敏锐度发展变得较为缓慢。马俊巍(2012)发现,小学阶段儿童在点数比较任务中的正确率同样随着年龄的增长而不断提高,但小学初期发展速度较缓慢。可见,儿童ANS敏锐度发展缓慢的年龄起点很可能可以扩展到学龄前5岁左右。
与以往研究不同,本研究还采用了点数异同任务来考察学前儿童ANS敏锐度的发展,其结果与点数比较任务较为一致,但是点数异同任务较难,这与Gebuis和van der Smagt(2011)的结果一致。其研究也指出,关于ANS敏锐度的婴儿研究采用的注视时间范式本质是一种点数异同判断任务,这样以往ANS敏锐度发展的研究结果不应当直接与婴儿数据进行对比,而应当采用同一实验范式来考察ANS的毕生发展。然而,点数比较任务不能运用于婴儿研究,因此采用点数异同任务来考察ANS的毕生发展可能更为合适。
4.2 ANS敏锐度各指标的相互关系在点数异同任务中,van Opstal和Verguts(2011)等认为,点数相同试次不包含被试表征数量的信息,通常将这部分试次不进行分析。本研究中,除韦伯系数与点数异同任务总正确率相关不显著外,其他ANS敏锐度的指标两两间均显著相关。可见除点数异同任务的总正确率外,其他几个指标具有共同的认知基础,都能用来反映个体ANS的敏锐度。然而这种关系是否可以通过一般认知能力来解释,未来研究需要做进一步探讨。
近年有研究者认为,点数比较任务测验结果可能混入了被试的抑制控制能力(Fuhs & McNeil, 2013; Gilmore et al., 2013)。本研究结果也支持了该假设,被试两种抑制控制任务的成绩均与点数比较任务的正确率显著正相关,与韦伯系数显著负相关。然而,抑制控制任务与点数异同任务中点数不同试次的正确率的相关不显著,此结果也支持了在点数异同任务中,被试的判断对点的视觉线索的依赖更小的假设,可见该指标反映了更为纯净的数表征能力(Gebuis & van der Smagt, 2011)。然而,点数异同任务难度要大于点数比较任务,说明点的非数量信息促进了点数比较任务中被试的成绩,或被试更难在点数异同任务中提取数量信息。然而本研究中已对非数量信息对整体正确率的促进作用进行了控制,因此更有可能的原因是后者,或者被试在点数异同任务中进行判断时能够使用的策略更少,如不能依赖数量的相对位置进行判断。
4.3 学前儿童ANS敏锐度与符号数学能力的关系首先,从不同任务及指标的差异来看。点数比较任务中,正确率与韦伯系数对符号数学能力各成分的预测作用不同。原因可能是,韦伯系数在具体计算中需要获得在每个比率条件下被试判断的正确率,通过曲线拟合来求得;而正确率则表示个体点数比较任务的成绩,它包含更多的信息。虽然van Opstal和Verguts(2011)提出,若被试作出判断是基于点的连续特性,如总面积、总周长来进行,则正确率可能并不具有很好的效度。但是相关研究也表明,韦伯系数指标用来表示幼儿的数量表征的敏锐程度可能并不可靠(Libertus et al., 2012; Mussolin et al,2014),Mazzocco等人(2011b)发现,点数比较任务的正确率与随后的数学成绩间显著相关而韦伯系数却不存在这种相关。本研究中参与实验的被试中,能拟合模型并求得韦伯系数的被试较少,并且与Libertus等人(2011)的研究相比实验任务较难,即使在最简单的比率条件下,3、4岁被试的正确率均小于75%,测得的韦伯系数可能不如正确率可靠。
本研究中,点数异同任务中仅有点数不同试次的正确率能显著预测符号数字知识,验证了van Opstal和Verguts(2011)的观点。因此,Gebuis和van der Smagt(2011)的研究结果未得出点数异同任务测得的近似数量敏锐度与符号数学能力间的相关,很可能是因为该研究使用总正确率为指标而没采用点数不同试次的正确率作为指标。
其次,从对符号数学能力各成分的预测作用来看。本研究结果发现在点数比较任务中,ANS敏锐度与数数能力、基数能力及符号数学知识显著相关,而与简易计算能力不相关。而点数异同任务下仅能预测符号数字知识。可见,ANS敏锐度可能对学前儿童掌握不同的符号数学能力的作用不同。对于ANS敏锐度与符号数学能力间的关系,研究者给出了不同的解释,Wynn(1992)认为,在儿童学习数字单词及阿拉伯数字时,需要将这些数字符号或单词与近似表征相匹配,这种近似的表征在没有学习数字符号时就已经存在,是获取数字符号意义的基础;Fuhs和McNeil(2013)则认为,早期数学经验是二者表现出相关的主要原因,尽管较小的儿童有能力进行近似的表征,但是他们只有在数学活动中才能真正使用它,并且通过不断使用才能使ANS变得越来越敏锐,这也增加了儿童在学习新的数学概念时对ANS的依赖。然而,二者显著相关并不能说明它们间的因果关系,如一些纵向研究表明,被试早期的数学能力或回忆的数学成绩与一段时间后的ANS敏锐度显著正相关(Halberda et al., 2012,2008; Libertus, Feigenson, & Halberda, 2013b),而ANS敏锐度却不能预测一段时间后的符号数字知识测验分数(Mussolin et al., 2014)。
另外,各种ANS敏锐度指标均不能显著预测简易加减成绩,原因可能是:首先,对于3~6岁儿童,相比于非符号的表征方式,可能符号表征对于算术运算起到的作用更大(Holloway & Ansari, 2009);其次,本研究是通过口头言语呈现的简易加减测验,可能被试的语言能力对测验的结果会有影响,回归分析中也发现,词汇测验的分数对简易加减的预测作用显著。最后,此结果可能也与学前儿童在进行算术运算时采用的策略有关。一部分学前儿童在进行算术运算时都不需要通过手指计数、最小加数这些策略,而是直接提取长时记忆的信息来完成这项任务,回归分析结果中也发现记忆测验的分数均能显著预测幼儿的简易加减成绩。结合相关研究可以推测(Lyons & Beilock, 2011),算术策略可能在ANS敏锐度与算术运算能力间起调节作用,需要进一步研究来进行验证。
在儿童群体中,计算障碍具有较高的发生率(张树东,董奇,2004)。而ANS的损害可能是计算障碍产生的原因(Mazzocco et al., 2011a)。心理学研究对人类健康的影响日益明显,ANS敏锐度与符号数学能力相互关系的研究可以为数学教育及对计算障碍被试的干预提供借鉴。近年来的几项训练研究就表明,对ANS敏锐度的训练对提高成人及小学儿童在算术运算的速度上有一定效果(Hyde, Khanum, & Spelke, 2014;Park & Brannon, 2013),但结论不一且迁移效果有限(Obersteiner, Reiss, & Ufer, 2012)。本研究则表明,未来的研究有必要考察这些训练方式是否适合于学前儿童,以及训练对除计算外的其他数学能力是否有效果。
| Barth, H., La Mont, K., Lipton, J., & Spelke, E. S. (2005). Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences, 102(39), 14116-14121. |
| Cantlon, J., Fink, R., Safford, K., & Brannon, E. M. (2007). Heterogeneity impairs numerical matching but not numerical ordering in preschool children. Developmental Science,10(4), 431-440. |
| Cantlon, J. F., Platt, M. L., & Brannon, E. M. (2009). Beyond the number domain. Trends in Cognitive Sciences, 13(2), 83-91. |
| Dewind, N. K., & Brannon, E. M. (2012,). Malleability of the approximate number system:Effects of feedback and training. Frontiers in Human Neuroscience.68(6), 1-10. |
| Diamond, A., & Taylor, C. (1996). Development of an aspect of executive control:Development of the abilities to remember what I said and to "Do as I say, not as I do." Developmental Psychobiology, 29(4), 315-334. |
| Fuhs, M. W., & McNeil, N. M. (2013). ANS acuity and mathematics ability in preschoolers from low-income homes:Contributions of inhibitory control. Developmental Science, 16(1), 136-148. |
| Gebuis, T., & van der Smagt, M. J. (2011). False approximations of the approximate number system? Plos One, 6(10), e25405. |
| Gerstadt, C. L., Hong, Y. J., & Diamond, A. (1994). The relationship between cognition and action:Performance of children 3.5-7 years old on a stroop-like day-night test. Cognition, 53(2), 129-153. |
| Gilmore, C., Attridge, N., Clayton, S., Cragg, L., Johnson, S., Marlow, N., Simms, V., et al. (2013). Individual differences in inhibitory control, not non-verbal number acuity, correlate with mathematics achievement. Plos One, 8(6), e67374. |
| Ginsburg, H. P., & Baroody, A. J. (1990). The Test of Early Mathematics Ability (2nd ed.). Austin, TX:Pro-Ed. |
| Halberda, J., & Feigenson, L. (2008). Developmental change in the acuity of the "Number Sense":The Approximate Number System in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology, 44(5), 1457-1465. |
| Halberda, J., L, R., Wilmer, J. B., Naiman, D. Q., & Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences, 109(28), 11116-11120. |
| Halberda, J., Mazzocco, M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455(7213), 665-669. |
| Holloway, I. D., & Ansari, D. (2009). Mapping numerical magnitudes onto symbols:The numerical distance effect and individual differences in children's mathematics achievement. Journal of Experimental Child Psychology, 103(1), 17-29. |
| Hyde, D. C., Khanum, S., & Spelke, E. S. (2014). Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. Cognition, 131(1), 92-107. |
| Jordan N. C., Kaplan D., Ramineni C., & Locuniak, M. N. (2009). Early math matters:Kindergarten number competence and later mathematics outcomes. Developmental Psychology,45(3), 850-867. |
| Klibanoff, R. S., Levine, S. C., Huttenlocher, J., Vasilyeva, M., & Hedges, L. V. (2006). Preschool children's mathematical knowledge:The effect of teacher"math talk."Developmental Psychology, 42(1), 59-69. |
| Libertus, M. E., Feigenson, L., & Halberda, J. (2011). Preschool acuity of the approximate number system correlates with school math ability. Developmental Science, 14(6), 1292-1300. |
| Libertus, M. E., Feigenson, L., & Halberda, J. (2013a). Numerical approximation abilities correlate with and predict informal but not formal mathematics abilities. Journal of Experimental Child Psychology, 116(4), 829-838. |
| Libertus, M. E., Feigenson, L., & Halberda, J. (2013b). Is Approximate Number Precision a Stable Predictor of Math Ability? Learning and Individual Differences, 25(2), 126-133. |
| Lourenco, S. F., Bonny, J. W., Fernandez, E. P., & Rao, S. (2012). Nonsymbolic number and cumulative area representations contribute shared and unique variance to symbolic math competence. Proceedings of the National Academy of Sciences, 109(46), 18737-18742. |
| Lyons, I. M., & Beilock, S. L. (2011). Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition, 121(2), 256-261. |
| Mazzocco, M. M. M., Feigenson, L., & Halberda, J. (2011a). Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia). Child Development, 82(4), 1224-1237. |
| Mazzocco, M. M. M., Feigenson, L., & Halberda, J. (2011b). Preschoolers' precision of the approximate number system predicts later school mathematics performance. Plos One, 6(9), e23749. |
| Mussolin, C., Nys, J., Content, A., & Leybaert, J. (2014). Symbolic number abilities predict later approximate number system acuity in preschool children. Plos One,9(3), e91839. |
| Mussolin, C., Nys, J., & Leybaert, J. (2012). Relationships between approximate number system acuity and early symbolic number abilities. Trends in Neuroscience and Education, 1(1), 21-31. |
| Obersteiner, A., Reiss, K., & Ufer, S. (2013). How training on exact or approximate mental representations of number can enhance first-grade students' basic number processing and arithmetic skills. Learning and Instruction, 23, 125-135. |
| Park, J., & Brannon, E. M. (2013). Training the approximate number system improves math proficiency. Psychological Science, 24(10), 2013-2019 |
| Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science, 306(5695), 499-503. |
| Van Opstal, F., & Verguts, T. (2011). The origins of the numerical distance effect:The same-different task. Journal of Cognitive Psychology, 23(1), 112-120. |
| Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358(6389), 749-750. |
| 马俊巍. (2012). 学龄儿童近似数量表征的研究. 硕士学位论文. 东北师范大学. |
| 王乃弋, 罗跃嘉, 李红. (2006). 两种数量表征系统. 心理科学进展,14(4), 610-617. |
| 张树东,董奇.(2004)发展性计算障碍的诊断与矫治.中国特殊教育,(2),21-25. |
 2016, Vol. 32
2016, Vol. 32


