国家教育部主管、北京师范大学主办。
文章信息
- 费广洪, 王淑娟, 秦梅梅. 2015.
- FEI Guanghong, WANG Shujuan, QIN Meimei. 2015.
- 提示对3~11岁儿童解决类比推理问题的影响
- The Influences of Hints 3~11 Years Old Children's Performance on Analogical Reasoning
- 心理发展与教育, 31(5): 578-585
- Acta Meteorologica Sinica, 31(5): 578-585.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2015.05.09
-
文章历史
类比推理(Analogical Reasoning)是人类认知发展的核心能力之一,是根据两类事物的结构相似性和一类事物已有的特征推出另一类事物也具有此特征的过程(王亚同,1999)。以往研究主要采用A∶B∷C∶D式类比任务和问题解决类比任务。20世纪70年代,Piaget首先采用A∶B∶∶C∶D式类比任务。80年代,研究者设计了类似于日常生活情景的问题解决任务。
纵观已有研究发现,研究者主要采用几何图形、关系图形、词语、数字和故事来研究类比推理,项目关系随着材料类型的变化而变化。几何图形中项目A、B的关系包括颜色、大小、形状等(Sternberg,1977; Alexander,Wilson,White,Wilson,& Tallent,1987;王亚同,1992; Thibaut,French,& Vezneva,2008; Tunteler,Pronk,& Resing,2008;赵顶位,戴海琦,2012);关系图形中项目A、B的关系主要有二元关系和三元关系等(Richland ,Morrison,& Holyoak,2006;马晓清,冯廷勇,李宇,李红,2008;辛自强,张莉,2010;王树芳,莫雷,金花,2010);数字中项目A、B的关系主要有相邻、等差、比例、组成与分解等(查子秀,1984;孙建梅,1997);词语中项目A、B的关系包括功能、并列、反义、包含、因果、整体与部分(Sternberg & Nigro,1980;张嘉玮,1980;刘建清,1995;Kostic,Cleary,Severin,& Miller,2010; Thibaut,French,& Vezneva,2010;赵鸣,徐知媛,刘涛,杜锋磊,李永欣,陈飞燕,2012);故事早期研究中主要用源问题“辐射问题”来解决“堡垒问题”(Holyoak,Junn,& Billman,1984; Antonietti,1991; Antonietti & Gioletta,1995; 邱琴,胡竹菁,闵容,2005; Catrambone,2006; Richland & McDonough,2010)。
纵观已有研究发现,研究者主要采用几何图形、关系图形、词语、数字和故事来研究类比推理,项目关系随着材料类型的变化而变化。几何图形中项目A、B的关系包括颜色、大小、形状等(Sternberg,1977; Alexander,Wilson,White,Wilson,& Tallent,1987;王亚同,1992; Thibaut,French,& Vezneva,2008; Tunteler,Pronk,& Resing,2008;赵顶位,戴海琦,2012);关系图形中项目A、B的关系主要有二元关系和三元关系等(Richland ,Morrison,& Holyoak,2006;马晓清,冯廷勇,李宇,李红,2008;辛自强,张莉,2010;王树芳,莫雷,金花,2010);数字中项目A、B的关系主要有相邻、等差、比例、组成与分解等(查子秀,1984;孙建梅,1997);词语中项目A、B的关系包括功能、并列、反义、包含、因果、整体与部分(Sternberg & Nigro,1980;张嘉玮,1980;刘建清,1995;Kostic,Cleary,Severin,& Miller,2010; Thibaut,French,& Vezneva,2010;赵鸣,徐知媛,刘涛,杜锋磊,李永欣,陈飞燕,2012);故事早期研究中主要用源问题“辐射问题”来解决“堡垒问题”(Holyoak,Junn,& Billman,1984; Antonietti,1991; Antonietti & Gioletta,1995; 邱琴,胡竹菁,闵容,2005; Catrambone,2006; Richland & McDonough,2010)。
提示是指在学习情境中通过明确指导语向被试说明源问题之间的关系(Richland et al., 2006;陈哲,王瑞明,莫雷,2008)。提示使儿童明确源问题之间的关系,从而使源问题和目标问题之间的同型结构关系凸现出来,以帮助儿童克服困难(冯廷勇,李宇,李红,苏缇,龙长权,2006)。类比推理的研究成果不仅能够揭示人类认知加工过程,而且对教育领域的作用也越来越明显(王树芳等,2010)。如果提示能够促进儿童类比推理的发展,则可以认为教育对儿童认识发展具有极大的促进作用。而推理是内在心理现象,如果发展成熟,那么从理论上来说,它应该是稳定的,不论使用什么材料研究所得出的结论都应该是一致的,但前人的研究结论并不一致。Richl and 等(2006)的研究发现,通过指导语向被试明确说明关系图形涉及的关系知识并不能提高测试成绩。但是,Loewenstein和Gentner(2005)研究发现44个月大的幼儿能在指导语提示关系的条件下成功完成任务,而49个月大的幼儿在提示和无提示条件下都能完成任务;Christie和Gentner(2007)使用新提示语言,而非儿童熟悉的提示语言。结果发现,在使用新提示语言的条件下,4.5岁和8.5岁儿童及成人的成绩都提高了。另外,冯廷勇等(2006)研究发现直接的关系提示能提高3、4岁儿童类比推理成绩,但不能提高5岁儿童成绩;而Gentner和Anggoro(2011)研究3~6岁儿童在有无提示条件下类比推理的成绩,结果发现,4、5岁儿童在提示条件下能完成类比推理,但3岁儿童却不行,6岁儿童在有无提示条件下均能完成类比推理。究其原因,可能是由于研究者各自只采用单一材料进行研究,导致结果存在很大的差异。不同研究者的指导语也不同。另外,年龄也可能是个影响因素。由于前人对类比推理发展年龄差异研究的结论不一致,甚至矛盾,本研究拟在前人研究的基础上,扩大研究对象的年龄范围,选取3~11岁儿童为被试,考察提示对不同年龄儿童影响的规律;同时,使用几何图形、关系图形、词语、数字、故事五种材料,考察提示对不同材料类比推理影响的规律,为促进儿童类比推理发展提供一定的依据。
2 实验方法 2.1 被试随机选取了4所幼儿园和4所小学,幼儿园为省级、市级、区级及新办园各1所,小学为省级、市级各1所,新办校2所。由主试在每所幼儿园和小学的各年级花名册中简单随机选取10名儿童作为被试。每一年龄儿童共40人,男女各半。3~11岁儿童共360人。3岁组儿童平均年龄为3岁7个月,标准差为2.18个月;4岁组儿童平均年龄为4岁8个月,标准差为3.21个月;5岁组儿童平均年龄为5岁6个月,标准差为3.23个月;6岁组儿童平均年龄为6岁7个月,标准差为3.11个月;7岁组儿童平均年龄为7岁6个月,标准差为3.13个月;8岁组儿童平均年龄为8岁7个月,标准差为3.55个月;9岁组儿童平均年龄为9岁3个月,标准差为3.92个月;10岁组儿童平均年龄为10岁2个月,标准差为3.21个月;11岁组儿童平均年龄为11岁4个月,标准差为3.95个月。
2.2 实验工具几何图形:反映大小、形状、数量、颜色、方向、位置、内外包含关系的几何图形共5套。例如  :
: ::
::  :?,选项:
:?,选项: 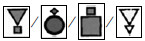 。
。
词语:反映从属、功能、对立、并列、整体与部分关系的词语各1套,共5套,配相应图片。例如:  ::
:: 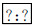 ,选项:
,选项: 
 。
。
数字:反映相邻、组成与分解、等差、相加、相减关系的数字共5套。例如:  ::
::  ,选项:
,选项: 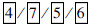 。
。
关系图形:反映二元关系(青蛙抓害虫;老鹰抓小鸡)、三元关系(人拉船,船拉木筏;人拉马,马拉车)等的图片共5套。
故事:“堡垒问题”和“辐射问题”、“森林问题”和“洞穴问题”、“称大象问题”和“称雕像问题”、“乌鸦喝水”和“皮球浮上来”、“水罐问题”和“绳子问题”的故事各一套,共5套,配相应图片。
每种材料各5套,五种材料共25题。每题选对计1分,选错计0分,每种材料满分为5分,五种材料共25道题,满分25分。
各种材料以公认有效的研究材料作为校标,具体而言,几何图形是Sternberg的研究材料,关系图形是Richl and 等的材料,词语是Sternberg和Nigro的研究材料,数字是查子秀的材料,故事Holyoak等的材料,效度分别是0.70、0.70、0.62、0.68、0.72,α信度分别是0.89、0.89、0.91、0.90、0.88。
2.3 实验设计采用9×5×2混合设计,9(年龄:3,4,5,6,7,8,9,10,11岁)×5(材料类型:几何图形,关系图形,词语,数字,故事)×2(提示条件:有,无),材料类型为被试内变量,年龄和提示条件为被试间变量。因变量为类比推理的成绩。
2.4 实验程序个别施测,每个儿童要做5份试题,随机顺序呈现试题,为防止疲劳,做完12道题中间休息5分钟。
首先主试给被试读指导语,然后请被试完成5道练习题,确定被试理解实验目的。如果被试经过三遍学习仍然不理解题意,则放弃该被试。主试向被试呈现源问题后,要求被试根据源问题的关系来解决目标问题。指导语因提示条件不同而变化,具体情况如下:
(1)有提示条件:先向儿童呈现源问题后,提示源问题之间的关系,然后呈现目标问题,要求儿童根据源问题的关系来解决目标问题。
①几何图形、词语、数字的指导语:“小朋友,你好!我们来玩个小游戏。(出示两张源图片)现在我们先看这两张图片(边说边指给被试看),它们是好朋友,它们都是……(提示类比关系,例如,水果和香蕉是整体和部分的关系),(出示第三张图片)现在我们再来看这张图片(边说边指给被试看),(出示四张备选图片)请你根据上面两个好朋友的关系,在下面四张图片中找一张跟它(指着第三张图片)成为好朋友。”
②关系图形的指导语:“小朋友,你好!我们来玩个小游戏。(出示源图片)现在我们先看这张图片(边说边指给被试看),它们是……(提示类比关系,例如,这是猫追老鼠,追的关系),(出示目标图片)我现在指上面这张图片中一个物体,请你在下面这张图片中找一个跟它关系相同的物体。”
③故事的指导语:“小朋友,你好!我们来玩个小游戏。现在我们先听第一个故事(出示源故事图片)……小朋友,你记住这个故事了吗?好,下面我们听第二个故事(出示目标故事图片),然后想想第一故事是如何解决的(提示源故事的解决方法),根据第一个故事的解决办法想想第二个故事该怎么办?”
(2)无提示条件:与有提示条件基本一致,不同之处是向儿童呈现源问题后不提示源问题之间的关系,其余的都相同。
被试1分钟不反应,即得0分,继续下一道题。被试反应后,主试记录被试对每道题的反应。
2.5 数据管理和分析采用SPSS16.0对数据进行管理和统计处理。
3 结果与分析研究对3~11岁儿童在不同提示条件下五种材料类比推理的成绩进行分析,结果如图 1、图 2和表 1所示:
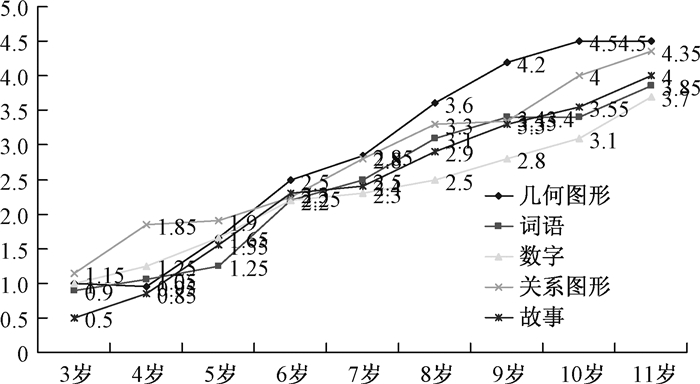 |
| 图 1 儿童在无提示条件下类比推理的平均成绩 |
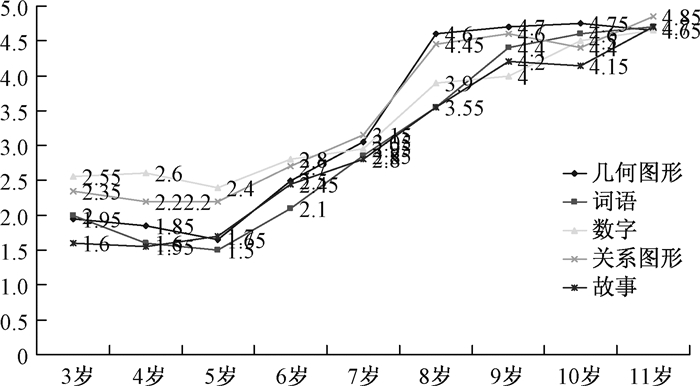 |
| 图 2 儿童在提示条件下类比推理的平均成绩 |
| 年龄 | 几何图形 | 词语 | 数字 | 关系图形 | 故事 | |||||
| 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | |
| M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | M(SD) | |
| 3 | 1.95(1.36) | 1.00(0.92) | 2.00(1.45) | 0.90(0.91) | 2.55(1.67) | 1.00(0.79) | 2.35(1.42) | 1.15(0.88) | 1.60(1.19) | 0.50(0.51) |
| 4 | 1.85(1.39) | 0.95(0.60) | 1.60(0.99) | 1.05(0.51) | 2.60(1.39) | 1.25(0.85) | 2,20(1.28) | 1.85(0.81) | 1.55(0.76) | 0.85(0.67) |
| 5 | 1.65(0.88) | 1.65(0.99) | 1.50(0.69) | 1.25(0.55) | 2.40(1.14) | 1.65(0.67) | 2.20(0.89) | 1.90(1.12) | 1.70(0.47) | 1.55(0.76) |
| 6 | 2.50(1.00) | 2.50(0.89) | 2.10(0.55) | 2.20(0.83) | 2.80(0.70) | 2.20(0.89) | 2.70(0.80) | 2.25(0.55) | 2.45(0.51) | 2.30(0.57) |
| 7 | 3.05(1.10) | 2.85(0.59) | 2.85(0.59) | 2.50(0.51) | 2.95(0.89) | 2.30(0.47) | 3.15(1.04) | 2.80(0.41) | 2.80(0.77) | 2.40(0.82) |
| 8 | 4.60(0.60) | 3.6(0.88) | 3.55(0.69) | 3.10(0.79) | 3.90(0.79) | 2.50(0.51) | 4.45(0.69) | 3.30(0.57) | 3.55(0.51) | 2.90(0.64) |
| 9 | 4.70(0.47) | 4.20(0.83) | 4.40(0.60) | 3.40(0.88) | 4.00(0.00) | 2.80(0.62) | 4.60(0.50) | 3.35(0.81) | 4.20(0.95) | 3.30(1.08) |
| 10 | 4.75(0.55) | 4.50(0.61) | 4.60(0.50) | 3.40(0.88) | 4.50(0.51) | 3.10(0.85) | 4.40(0.50) | 4.00(0.72) | 4.15(0.59) | 3.55(0.69) |
| 11 | 4.65(0.49) | 4.50(0.69) | 4.70(0.47) | 3.85(0.88) | 4.65(0.49) | 3.70(0.86) | 4.85(0.37) | 4.35(0.67) | 4.70(0.47) | 4.00(0.92) |
由图 1可见,在无提示条件下,3~11岁儿童各材料类比推理成绩基本随着年龄的增长而提高。由图 2可见,在提示条件下,3~11岁儿童各材料类比推理成绩并非随年龄增长而呈直线提高。
结果表明,在无提示条件下,儿童的类比推理的正确率基本随着年龄的增加而提高;但是在提示条件下,儿童的类比推理的正确率并非随年龄的增长而呈直线提高。
研究将各材料原始分数在SPSS软件中转化成标准分数,是同年龄转化。对儿童的类比推理成绩进行了2(提示条件)×9(年龄)×5(材料类型)的方差分析,结果表明:年龄的主效应显著,F(1,342)=248.74,p<0.001,η2=0.85,说明不同年龄的类比推理成绩之间有显著性差异;提示条件的主效应显著,F(1,342)=212.05,p<0.001,η2=0.38,说明不同提示条件的类比推理成绩之间有显著性差异;材料类型的主效应不显著,说明不同类型材料的类比推理成绩之间无显著性差异;年龄与提示条件交互作用显著,F(8,342)=5.26,p<0.001,η2=0.11;年龄与材料类型交互作用显著,F(32,1368)=2.45,p<0.001,η2=0.05;提示条件与材料类型交互作用显著,F(4,1368)=13.26,p<0.001,η2=0.03;年龄、材料类型与提示条件交互作用不显著。
| (%) | |||||||||||
| 年龄 | 几何图形 | 词语 | 数字 | 关系图形 | 故事 | ||||||
| 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | 有提示 | 无提示 | ||
| 3 | 39 | 20 | 40 | 18 | 51 | 20 | 47 | 23 | 32 | 10 | |
| 4 | 37 | 19 | 32 | 21 | 52 | 25 | 44 | 37 | 31 | 17 | |
| 5 | 33 | 33 | 30 | 25 | 48 | 33 | 44 | 38 | 34 | 31 | |
| 6 | 50 | 50 | 42 | 44 | 56 | 44 | 54 | 45 | 49 | 46 | |
| 7 | 61 | 57 | 57 | 50 | 59 | 46 | 63 | 56 | 56 | 48 | |
| 8 | 92 | 72 | 71 | 62 | 78 | 50 | 89 | 66 | 71 | 58 | |
| 9 | 94 | 84 | 88 | 68 | 80 | 56 | 92 | 67 | 84 | 66 | |
| 10 | 95 | 90 | 92 | 68 | 90 | 62 | 88 | 80 | 83 | 71 | |
| 11 | 93 | 90 | 94 | 77 | 93 | 74 | 97 | 87 | 94 | 80 | |
因为提示条件与材料类型存在交互作用,需要进一步做简单效应分析,结果发现,在几何图形中,提示条件的简单效应均显著(p<0.01);在词语中,提示条件的简单效应均显著(p<0.01);在数字中,提示条件的简单效应显著(p<0.01);在关系图形中,提示条件的简单效应显著(p<0.01);在故事中,提示条件的简单效应显著(p<0.01)。说明,提示可以提高几何图形、词语、数字、关系图形和故事类比推理的成绩。在有提示中,材料类型条件的简单效应均显著;无提示中,材料类型条件的简单效应均显著。
进一步比较提示对每种材料在各年龄中类比推理成绩的影响。抽取同一种材料(例如几何图形)来分析提示对不同年龄影响的差异是否显著,只有提示和年龄两个变量,因此只能做t检验。结果发现,几何图形中,3、4、8、9岁的提示条件差异显著,t=2.59,p<0.05;t=2.66,p<0.01;t=4.19,p<0.01;t=2.34,p<0.01,而5、6、7、10、11岁的提示条件差异不显著。词语中,3、4、9、10、11岁的提示条件差异显著,t=2.87,p<0.01;t=2,20,p<0.01;t=4.20,p<0.01;t=5.28,p<0.01;t=3.83,p<0.01,而5、6、7、8岁的提示条件差异不显著。数字中,3、4、5、6、7、8、9、10、11岁的提示条件差异显著,t=3.74,p<0.001;t=3.70,p<0.01;t=2.53,p<0.01;t=2.37,p<0.01;t=2.90,p<0.01;t=6.66,p<0.01;t=8.72,p<0.01;t=6.29,p<0.01;t=4.28,p<0.01。关系图形中,3、8、9、10、11岁的提示条件差异显著,t=3.21,p<0.01;t=5.76,p<0.01;t=5.85,p<0.01;t=2.02,p<0.01;t=2.93,p<0.01,而4、5、6、7差异不显著。故事中,3、4、8、9、10、11岁的提示条件差异显著,t=3.80,p<0.001;t=3.09,p<0.01;t=3.55,p<0.01;t=2.80,p<0.01;t=2.97,p<0.01;t=3.04,p<0.01,而5、6、7岁的提示条件差异不显著。
4 讨论 4.1 提示对同一材料不同年龄儿童类比推理的影响不同本研究发现,提示对不同年龄儿童的影响存在差异,与冯廷勇等(2006)关于提示对儿童解决类比推理问题的影响是非线性的结论是一致的。
结果表明,在几何图形类比推理中,提示对不同年龄儿童类比推理影响是不同的。研究发现,提示对3~4岁儿童几何图形类比推理有影响。几何图形虽然是幼儿园中常规的学习内容,幼儿比较熟悉,但是3~4岁儿童思维具有直觉行动性和具体形象性,而几何图形的源问题、目标问题和备选项包含着较多的元素,儿童要从具体的几何图形中抽取出抽象的关系还是存在困难的。在无提示的条件下,3~4岁儿童的类比推理成绩低于概率水平,儿童不会类比推理。主试对源问题和目标问题关系的提示强化了儿童要根据关系进行类比推理,儿童能对自己理解的事物之间外部关系进行迁移,即根据“低层次关系”进行类比推理。查子秀(1984)研究发现,3岁和4岁儿童几何图形类比推理的正确率仅仅是7.1%和19.2%,儿童还不会类比推理,而本研究发现经过提示以后,3岁和4岁儿童类比推理的正确率达到39%和37%。但是,提示对5~7岁儿童的几何图形类比推理影响不显著。由于这个年龄的儿童处于从前运算向具体运算阶段过渡时期,主要采用联想的方式进行类比推理,属于“低层次关系”类比推理(Piaget,1977),即使主试提示了源问题中事物之间的关系,但是由于儿童的知识经验有限,仍然不理解源问题事物之间关系的含义,所以,无法将源问题之间关系映射到目标问题中。当儿童成长到8~9岁已经能够理解源问题之间的关系,能够根据关系进行类比推理,但会受到外部特征干扰,表现不稳定。经过提示以后,儿童能抑制表面相似性的干扰,稳定地依据关系进行类比推理。到了10~11岁儿童已经非常熟悉几何图形,对其进行类比推理比较容易,即使主试不提示关系,儿童也能进行类比推理。因此,提示对10~11岁儿童影响不显著。
结果表明,在词语类比推理中,提示对不同年龄儿童类比推理影响是不同的。儿童要进行词语类比推理,首先要理解源问题中词语的涵义,例如, ,儿童要抽取出源问题词语之间所包含的抽象关系——整体与部分,最后将源问题之间的关系迁移到目标问题——
,儿童要抽取出源问题词语之间所包含的抽象关系——整体与部分,最后将源问题之间的关系迁移到目标问题—— 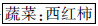 。对3~4岁儿童来说这些关系比较抽象,要独立抽取和迁移这些抽象关系比较困难。经过提示以后,儿童开始意识到词语所代表的事物之间具有某种关系,开始尝试能够根据这些抽象关系进行推理,从根本不会类比推理转变为开始能够进行类比推理,但是水平很低。查子秀(1984)研究发现,3岁和4岁儿童类比推理的正确率仅仅是2.3%和6.9%,儿童不会类比推理,而本研究发现经过提示以后,3岁和4岁儿童类比推理的正确率达到40%和32%,说明提示能促进儿童类比推理。但是提示对5~8岁儿童词语类比推理没有显著影响。这个年龄的儿童虽然意识到要根据关系进行推理,但是由于知识经验不够丰富,抽象逻辑思维发展水平较低,仍然难于理解词语所代表的事物之间的抽象关系,例如整体与部分关系,功能关系,所以,提示的作用难于见效。当儿童成长到9~11岁时,处于具体运算阶段,其抽象逻辑思维有所发展,基本能够理解词语所代表的事物之间的抽象关系。但是,日常经验仍然对其起着重要的作用,所以,在儿童独立进行类比推理时,会受到同一类别特征干扰,表现不稳定,例如,源问题为
。对3~4岁儿童来说这些关系比较抽象,要独立抽取和迁移这些抽象关系比较困难。经过提示以后,儿童开始意识到词语所代表的事物之间具有某种关系,开始尝试能够根据这些抽象关系进行推理,从根本不会类比推理转变为开始能够进行类比推理,但是水平很低。查子秀(1984)研究发现,3岁和4岁儿童类比推理的正确率仅仅是2.3%和6.9%,儿童不会类比推理,而本研究发现经过提示以后,3岁和4岁儿童类比推理的正确率达到40%和32%,说明提示能促进儿童类比推理。但是提示对5~8岁儿童词语类比推理没有显著影响。这个年龄的儿童虽然意识到要根据关系进行推理,但是由于知识经验不够丰富,抽象逻辑思维发展水平较低,仍然难于理解词语所代表的事物之间的抽象关系,例如整体与部分关系,功能关系,所以,提示的作用难于见效。当儿童成长到9~11岁时,处于具体运算阶段,其抽象逻辑思维有所发展,基本能够理解词语所代表的事物之间的抽象关系。但是,日常经验仍然对其起着重要的作用,所以,在儿童独立进行类比推理时,会受到同一类别特征干扰,表现不稳定,例如,源问题为  ,部分儿童据此推出
,部分儿童据此推出 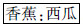 。经过提示以后,儿童能抑制同一类别特征相似性的干扰,稳定地依据关系进行类比推理。刘建清(1995)研究发现9岁儿童能完成一半的类比推理任务,而本研究发现9岁儿童在有提示条件下的类比推理正确率达到88%,远远高于刘建清的研究结果。
。经过提示以后,儿童能抑制同一类别特征相似性的干扰,稳定地依据关系进行类比推理。刘建清(1995)研究发现9岁儿童能完成一半的类比推理任务,而本研究发现9岁儿童在有提示条件下的类比推理正确率达到88%,远远高于刘建清的研究结果。
结果表明,在关系图形类比推理中,提示对不同年龄儿童类比推理影响是不同的。3岁儿童基本不会进行关系图形类比推理,经过提示关系以后,儿童开始意识到要根据关系进行推理,而关系图形呈现的关系基本都是日常生活情境,例如,狗追猫,猫追老鼠,这些3岁儿童基本能够理解,所以,3岁儿童开始能对关系图形进行类比推理。到了4~7岁,因为类比推理中所包含的关系是儿童日常生活中熟悉的关系,所以,不论提示与否,儿童都能够根据关系进行类比推理。所以,提示的作用不显著,只是这阶段儿童的类比推理仍然会受到表面特征的干扰。到了8~11岁儿童进行类比推理时会受到外部特征干扰。例如,源问题是小熊娃娃装在箱子里,目标问题是书装在书包里,旁边放了一只小熊娃娃,要求儿童在目标问题中选出与源问题小熊娃娃的关系相同的物体,部分儿童会选择错误答案小熊娃娃,而不是正确答案书。而提示帮助儿童抑制了事物之间的外部特征干扰,从而能够稳定地根据关系进行推理。王树芳等(2010)研究发现,10~11岁儿童类比推理的正确率低于50%,而本研究在提示条件下儿童类比推理的正确率达到88%~97%。
结果表明,在故事类比推理中,提示对不同年龄儿童类比推理的影响是不同的。故事类比推理实际上反映的是问题解决策略的类比推理。儿童首先要发现源问题中的问题情境与目标问题中的问题情境是一致的,才能够推理出同样的问题解决策略。儿童故事类比推理的发展受到多因素制约,而且是非常复杂的动态过程,总体来说是呈上升的趋势,但局部可能是波浪式的前进(陈英和,赵笑梅,2007)。在无提示条件下,3~4岁儿童更多关注故事类比推理中具体情境的表面相似性,而故事中包含抽象的关系,儿童从源故事中抽取出抽象的关系迁移到目标故事中是比较困难的。而经过主试提示后,儿童才开始有意识去思考源故事与目标故事之间的关系,能够初步进行类比推理,正确率达到31%~32%。到了5~7岁,儿童开始关注结构相似性,但是故事涉及到的关系复杂,有多个学科的知识。即使经过提示,儿童知道要根据关系进行类比推理,但是,仍然不能发现源问题和目标问题之间具有相同的问题情境,不能找出二者之间相同的结构关系,所以,提示不能带来儿童问题解决类比推理结果的变化。因为类比推理的最后一个阶段是运用所获得的策略和规则,当源问题和目标问题之间只是解决问题的基本规则相同,但是具体程序不同,即使提示了源问题的解决策略,儿童在解决目标问题时也会遇到困难(Chen,2002)。这一结果与冯廷勇等(2006)研究结果一致,即提示对5岁左右儿童类比推理的影响不显著。儿童发展到小学中高年级,抽象思维发展起来了,相关领域的知识也越来越丰富,在无提示条件下儿童故事类比推理成绩是58%~80%。而经过成人提示以后,能够发现源问题和目标问题之间的结构关系,能将源问题解决策略迁移到目标问题中,正确率达到71%~94%。Chen(1999)研究也发现给9岁儿童提供明确的指导,儿童能够有效把问题解决策略迁移到结构相似的其它问题中。
4.2 提示帮助儿童明确了源问题之间的关系,从而促进了类比推理儿童解决类比推理问题首先需要编码和表征源问题,然后感知类比关系,激活了类比源,即知道源问题之间的关系以及源问题与目标问题之间的关系,最后就是运用获得策略(陈哲等,2008)。如果儿童不了解源问题之间是什么关系,那么,是无法实现类比推理的。而提示明确告诉了儿童源问题之间的关系,例如,在词语类比推理中提示儿童这两个词语是整体与部分的关系;几何图形类比推理中提示了两个图形的颜色和形状不同;数字类比推理中提示了两个数字是相加的关系。这使原本没有发现源问题之间关系的儿童知道了源问题之间的关系,不需要再自己激活类比源。但是,经过提示后,不同年龄儿童词语和几何图形类比推理成绩变化的规律不同,这可能与提示的功效是否充分发挥有关。小学低年级儿童经提示后类比推理成绩仍然无变化,这可能是因为儿童不理解提示所指关系的含义,如不理解整体与部分关系,所以,无法将源问题之间的关系迁移到目标问题中。而高年级儿童就能够理解提示所指关系的含义,能够将源问题中获得的关系迁移到目标问题中,所以,提示后高年级儿童的类比推理成绩有提高。
但是,数字类比推理的题目特点不同于其他材料,例如,给儿童呈现源问题三个数字  ,以及目标问题两个数字
,以及目标问题两个数字  ,要求儿童根据前面一组数字之间的关系,以及前面一组数字与后面一组数字的关系相同,推出后面一组数字中的最后一个数字。由于源问题只有一组,其中就会包含多种可能关系,例如相邻、等差、相加、相减、组成与分解等关系,使儿童无法确认源问题数字之间的关系。成人的提示帮助儿童激活了源问题之间的关系,使儿童知道了源问题几个数字之间是相加关系。儿童一旦发现了潜在的结构关系,就能更好地进行类比推理迁移,特别是年龄较小的儿童(Chen & Daehler,1992)。另外,由于数字之间的相邻、加减、等差关系是儿童能够理解的关系,所以,提示能够有效提高各个年龄儿童数字类比推理的成绩。
,要求儿童根据前面一组数字之间的关系,以及前面一组数字与后面一组数字的关系相同,推出后面一组数字中的最后一个数字。由于源问题只有一组,其中就会包含多种可能关系,例如相邻、等差、相加、相减、组成与分解等关系,使儿童无法确认源问题数字之间的关系。成人的提示帮助儿童激活了源问题之间的关系,使儿童知道了源问题几个数字之间是相加关系。儿童一旦发现了潜在的结构关系,就能更好地进行类比推理迁移,特别是年龄较小的儿童(Chen & Daehler,1992)。另外,由于数字之间的相邻、加减、等差关系是儿童能够理解的关系,所以,提示能够有效提高各个年龄儿童数字类比推理的成绩。
而在故事类比推理中,提示只是间接地笼统地要求儿童根据源问题的解决方法去思考目标问题的解决方法,如,要求儿童根据源问题,想一想怎样解决目标问题,对于幼儿园低年级儿童来说,提示有助于儿童解决目标问题。以往研究发现,年龄较小的儿童在故事类比推理中更加倾向于借助表面特征而不是结果特征,并且他们更加依赖于问题关系的提示信息(Daehler & Chen,1993; Chen,1996)。而幼儿园高年级和小学低年级儿童难于发现源问题和目标问题之间的相同之处,无法激活类比源,提示效果不明显。而到了小学高年级,儿童本身知识经验大大增加,经过提示以后,能够发现源问题与目标问题之间具有相同的问题情境,因而,能够将源问题的解决策略迁移到目标问题上。
与故事类比推理不同的是,在关系图形类比推理中,虽然提示也是笼统地要求儿童找到关系相同的事物,如,告诉儿童这是猫追老鼠,要求儿童在另一种情境中找一个跟猫相同关系的物体,由于关系图形中呈现的情境是儿童日常所熟悉的情境,儿童比较容易发现源问题之间的关系,以及源问题与目标问题之间的关系是一致的,所以,提示对小学低年级儿童效果不明显。小学高年级儿童类比推理的正确率不够高是因为关系图形中还含有分心物,干扰了儿童对于关系的映射。而提示强化了关系相同的概念,从而帮助了小学高年级儿童抑制了分心物的干扰。
4.3 提示使原本不会类比推理的3岁儿童能够初步进行类比推理方差分析结果表明,3岁儿童的五种材料类比推理成绩在两种提示条件下均存在显著性差异。由表 1也可见,在无提示条件下,3岁儿童五种类比推理的正确率分别为20%、18%、20%、23%、10%,均低于概率水平,说明,3岁儿童不会类比推理;在提示条件下,3岁儿童五种类比推理的成绩分别为39%、40%、51%、47%、32%,超过了概率水平。可见,3岁儿童经过提示能够进行类比推理,但水平还比较低。Gentner,Loewenstein和Thompson(2003)发现结构相似性对类比推理影响较大,儿童不能类比推理是因为他们不能发现源问题和目标问题之间的结构相同。3岁儿童处于前运算阶段,思维具有直觉行动性和具体形象性,主要依据表面相似性进行类比推理,经过提示后,儿童开始意识到要根据关系进行类比推理,对于自己能够理解的源问题之间的关系以及源问题与目标问题之间的关系即能进行类比推理。但是,由于3岁儿童知识经验缺乏,能够理解的事物之间的关系有限,又会受到分心物的干扰,因此,只能成功进行少量的类比推理。
5 结论(1)提示对3~4岁、8~9岁儿童几何图形类比推理成绩有影响,对5~7岁、10~11岁儿童类比推理成绩无影响。提示对3~4岁、9~11岁儿童词语类比推理成绩有影响,对5~8岁儿童类比推理成绩无影响。提示对3~11岁儿童数字类比推理成绩均有影响。提示对3、8~11岁儿童关系图形类比推理成绩有影响,对4~7岁儿童类比推理成绩无影响。提示对3~4岁、8~11岁儿童故事类比推理成绩有影响,对5~7岁儿童类比推理成绩无影响。
(2)提示使原本不会类比推理的3岁儿童能够初步进行类比推理。
| Alexander, P. A., Wilson, A. F., White, C. S., Willson, V. L., Tallent, M. K., & Shutes, R. E. (1987). Effects of teacher training on children's analogical reasoning performance.Teaching & Teacher Education,3(4), 275-285. |
| Antonietti, A. (1991). Effects of partial analogies on solving an ill-defined problem.Psychological Reports,68, 947-960. |
| Antonietti,A., & Gioletta,M.A. (1995). Individual differences in analogical problem solving.Personality and Individual Differences,18,611-619. |
| Chen,Z.(1996). Children's analogical transfer: Effects of superficial, structural and procedural similarity.Journal of ExperimentalChild Psychology,62, 410-431. |
| Chen,Z. (1999). Schema induction in children's analogical problem solving.Journal of Educational Psychology, 91,703-715. |
| Chen,Z. (2002). Analogical problem solving: A hierarchical analysis of procedural similarity.Journal of Experimental Psychology: Learning, Memory, & Cognition,28, 81-98. |
| Chen, Z., & Daehler, M. W. (1992). Intention and outcome: Key components of causal structure facilitating mapping in children's analogical transfer.Journal of Experimental Child Psychology,53(3), 237-257. |
| Christie, S., & Gentner, D. (2007). Relational similarity in identity relation: The role of language. In Vosniadou, S. & Kayser, D. (Eds.).Proceedings of the Second European Cognitive Science Conference. |
| Crisafi, M.A., & Brown, A. L. (1986). Analogical transfer in very young children: Combining two separately learned solutions to reach a goal.Child Development,57, 953-968. |
| Daehler, M. W., & Chen, Z. (1993). Protagonist, theme, and goal object: Effects of surface features on analogical transfer. Cognitive Development, 8(2), 211-229. |
| Tunteler, E., Pronk, C.M., & Resing W. C.(2008).Inter-and intra-individual variability in the process of change in the use of analogical strategies to solve geometric tasks in children: A microgeneticanalysis.Learning and Individual Differences,18,44-60. |
| Gentner, D., & Anggoro,F.K. (2011). Structure Mapping and Relational Language Support Children's Learning of Relational Categories. Child Development, 82,1173-1188. |
| Gentner, D., Loewenstein, J., & Thompson, L. (2003).Learning and transfer: A general role for analogical encoding.Journal of Educational Psychology,2,393-408. |
| Holyoak, K. J., Junn, E. N., & Billman, D.O.(1984). Development of analogical problem-solving skill. Child Development, 55(6),2042-2055. |
| Kostic, B., Cleary, A. M.,Severin, & Miller,S.W. (2010). Detecting analogical resemblance without retrieving the source analogy.Psychonomic Bulletin & Review, 17(3), 405-411. |
| Loewenstein, J., & Gentner, D. (2005). Relational language and the development of relational mapping.Cognitive Psychology,50,315-353. |
| Piaget, J., Montangero, J., & Billeter, J. (1977).La formation des correlats.In J. Piaget (Ed.),Recherches surl'abstraction reflechissante I.Paris: Presses Universitaires de France, 115-129. |
| Richard C., (2006). The effects of surface and structural feature matches on the access of story analogs.Journal of Experimental Psychology: Learning, Memory, and Cognition,28(2), 318-334. |
| Richland, L. E., & McDonough,IM. (2010).Learning by analogy: Discriminating between potential analogs.Contemporary Educational Psychology,35,28-43 . |
| Richland, L. E., Morrison, R. G., & Holyoak,K. J. (2006). Children's development of analogical reasoning: Insights from scene analogy problems.Journal of Experimental Child Psychology,94(3), 249-273. |
| Sternberg, R. J. (1977). Component processes in analogical reasoning.Psychological Review, 31, 356-378. |
| Sternberg, R. J., & Nigro, G. (1980).Developmental patterns in the solution of verb-alanalogies.Child Development, 51, 27-83. |
| Thibaut, J. P., French, R., & Vezneva, M. (2008). Analogy-making in children: the importance of processing constraints, 30th annual meeting of the cognitive science society, Washington, DC. |
| Thibaut,J.P., French,R.,& Vezneva,M.(2010). Cognitive load and semantic analogies: Searching semantic space.Psychonomic bulletin & review, 17(4), 569-574. |
| 查子秀.(1984). 3-6岁超常与常态儿童类比推理的比较研究.心理学报,16(4), 373-382. |
| 陈英和, 赵笑梅. (2007). 小学3~5年级儿童类比问题解决及策略运用发展.心理发展与教育,(2), 18-22. |
| 陈哲, 王瑞明,莫雷. (2008). 儿童问题解决中的类比迁移.心理科学进展,16(1), 65-70. |
| 冯廷勇, 李宇, 李红, 苏缇, 龙长权. (2006). 3~5岁儿童表面与结构相似性类比推理的实验研究.心理科学, 29(5), 1091-1095. |
| 刘建清. (1995). 9~12岁儿童类比推理能力的发展.心理科学, 18(1), 56-58. |
| 马晓清, 冯廷勇, 李宇, 李红. (2008). 从知觉分心任务看儿童类比推理能力的发展.心理学报,40, 987-993. |
| 邱琴, 胡竹菁, 闵容. (2005). 影响图式归纳和类比迁移的三因素实验研究.心理科学, 28(6), 92-96. |
| 孙建梅. (1997). 7~12岁儿童类比推理能力发展研究.新疆教育学院学报, (2), 9-12. |
| 王树芳, 莫雷, 金花.(2010). 任务难度和反馈学习对儿童类比推理能力的影响.心理发展与教育, (1), 24-30. |
| 王亚同. 1999. 类比推理. 保定: 河北大学出版社. |
| 王亚同. (1992). 3.5~5岁儿童类比推理的实验研究.心理发展与教育,(4), 10-16. |
| 辛自强, 张莉. (2010). 5~9岁儿童在不同复杂性任务上类比推理的发展特点.心理发展与教育, (6), 584-591. |
| 张嘉玮. (1980). 藏族和汉族小学儿童类比推理过程中思惟发展特点的比较.心理学报, (4),406-414. |
| 赵顶位,戴海琦.(2012).4-8年级学生几何类比推理问题解决认知诊断.心理学探新, 32,(1),77-81. |
| 赵鸣,徐知媛,刘涛,杜锋磊,李永欣,陈飞燕.(2012).语言类比推理的神经机制:来自 ERP研究的证据.心理学报,(6),711-719. |
 2015, Vol. 31
2015, Vol. 31


