国家教育部主管、北京师范大学主办。
文章信息
- 张帆, 赖颖慧, 陈英和. 2015.
- ZHANG Fan, LAI Yinghui, CHEN Yinghe. 2015.
- 儿童数字线表征的发展——心理长度的影响
- Development of Children's Number Line Estimation: the Influence of Mental Distance
- 心理发展与教育, 31(2): 149-156
- Acta Meteorologica Sinica, 31(2): 149-156.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2015.02.03
-
文章历史
数量表征(numerical representation)指个体心理对数量刺激的解释、表达与操作的过程(Brysbaert,2005),数量表征的发展是近年来研究者关注的重要问题。儿童存在对数表征和线性表征两种数量表征模式,其中对数表征是不精确的,是对客观数量的对数压缩,扩大了小数之间的差距,缩小了大数之间差距,因此数量越大,儿童越难以区分数量之间的差异(Dehaene,1997);相反,线性表征是精确的,儿童对每个客观数量的表征没有差异(莫雷,周广东,温红博,2010)。
为了探索儿童数量表征模式的发展特点,Siegler和Opfer(2003)使用给位置标数字(position to number,PN)和给数字标位置(number to position,NP)两种数字线估计任务测量了二、四、六年级儿童和成人的数量表征能力。结果发现,在一定的数量范围内,随着年龄的增长,儿童的表征模式逐渐从对数(NP任务中符合对数函数模型)或指数表征(PN任务中符合对指数函数模型)发展为线性表征;在同年龄被试中,数字线的数量范围越小,被试越可能运用线性表征。
Siegler和Opfer(2003)提出了多重表征模型(Multiple Representations of Numerical Quantity)解释以上结果,他们认为:(1)个体可能同时有多种表征模式;(2)个体使用哪种表征由具体情境决定,数量范围越小,越可能使用线性表征;(3)随着年龄的增长,个体会更加依靠线性表征。多重表征模型得到了很多研究的证实,大量研究都发现儿童的表征会呈现从非线性到线性模式的发展规律(Berteletti,Lucangeli,Piazza,Dehaene,& Zorzi,2010; Siegler & Booth,2004; Siegler & Mu,2008)。除了表征模式的发展,儿童估计的精确性也出现从不精确到精确的变化。有研究表明,一、二年级儿童的估计精确性高于学龄前儿童,而三、五年级儿童估计的精确性高于一年级儿童,说明随着年龄的增长,儿童估计的精确性不断提高(周广东,莫雷,温红博,2009)。这与儿童的表征模式从非线性到线性发展的趋势是一致的。
但近年来,越来越多的研究者对多重表征模型提出了质疑。首先,一些研究者反对用对数和指数模型解释儿童早期表征;他们根据儿童在数字线NP任务中对小数易高估、对大数估计较为准确的特点提出了分段线性模型(decomposed linear model)。有研究证实,在0~100数字线中找到一个数字作为拐点,对拐点前后的估计值分别计算不同的线性函数得到的分段线性模型能比线性或对数模型更好地解释儿童数字线估计的数据(Ebersbach,Luwel,Frick,Onghena,& Verschaffel,2008; Moeller,Pixner,Kaufmann,& Nuerk,2009)。但相比对数或线性模型,分段线性模型使用了更多参数,存在增加参数以加大模型解释率的可能性,而且不同学者对分段模型拐点界定的差异较大;加之分段线性模型只能解释儿童在数字线估计任务中的表现,使用范围比较有限,因此该理论还存在较大的缺陷(Booth & Siegler,2006)。
其次,Barth和Paladino(2011)还提出数字线估计任务包含了比例判断,被试可通过估计中点、四分位点等参照点帮助他们进行数量估计,因此可以使用以中点或者四分位点为拐点的单/双周期比例模型(one- or two-cycle proportion model)解释儿童的数字线表征。Barth和Paladino发现,比例模型对5岁和7岁儿童0~100数字线估计数据的解释率高于线性和对数模型。但也有研究者发现,比例模型的优势并不是绝对的,Opfer,Siegler和Young(2011)对7组已有研究的数据进行了重新分析,并对线性、对数和比例模型进行了比较,结果没有发现比例模型的优势,仍支持多重表征模型。
由于比较模型解释率的高低难以真正说明多重表征模型的不足,近期有研究者从儿童数字线估计策略发展的角度,探寻导致其估计结果符合不同函数模型的可能原因;并提出随着儿童的发展,他们的估计策略发生了变化,这才是导致他们的估计结果符合不同函数模型的原因。如Slusser,Santiago和Barth(2013)的研究发现,学前儿童还不能使用中点作为参照,但是随着儿童的发展,他们逐渐掌握了通过判断参照点位置提高估计精确性的方法。因此,他们认为儿童表征的发展可能是一个连续的过程,并未出现表征模式的替换,该观点与多重表征模型的观点相反。中国学者莫雷等人(2010)考察了学龄初期儿童的估计过程,发现不当的估计策略导致年幼儿童的估计不符合线性模型。他们的研究包含两项实验:实验一设置了15cm的0~100和0~1000数字线NP任务,结果发现一年级儿童对0~100数字线的表征更符合线性模型,对0~1000数字线的表征更符合对数模型,而且儿童在两种条件下对低端数字(1~10)的估计值没有差异;实验二设置了10cm和20cm的0~1000数字线NP任务,结果一年级儿童对10cm数字线的表征更符合对数模型,而20cm数字线的线性和对数表征模型解释率相同,并且儿童在这两种条件下对低端数字的估计值也不存在差异。
由此,莫雷等人(2010)提出了“心理长度”(mental distance)的概念,他们认为儿童之所以会出现从非线性到线性表征的变化,是因为他们对“1”赋予了心理长度,并通过叠加心理长度的方式对低端数值(1~10)进行估计。由于心理长度的存在,导致儿童在数量范围较大和数字线较短的数字线NP任务中对低端数字存在高估的倾向,使表征模式在统计上符合对数函数模型。因此,心理长度是儿童在不同数字范围和不同数字线长度中采用不同表征模式的根本原因。
可见,心理长度能解释儿童早期出现非线性表征的原因,真正挑战了多重表征模型。但当前有关心理长度的研究还不充分,仍有以下问题需要解决:首先,儿童在数字线估计任务中通过累加心理长度进行估计的行为实质上反映了儿童对数的认识停留在等距水平,他们只能使用数数策略完成估计任务(莫雷等,2010)。随着儿童的发展,他们在估计任务中会逐渐放弃数数策略(van Viersen,Slot,Kroesbergen,Van'T Noordende,& Leseman,2013),这是否会导致儿童不再出现心理长度现象?如果心理长度消失,是突然消失还是逐渐消退?其次,如果心理长度是影响表征模式发展的原因,那么随着心理长度的消失,儿童的表征模式是否随之出现从对数表征到线性表征的发展?回答这些问题需要检验不同年龄段儿童对不同长度数字线估计的差异,并分析心理长度与表征模式发展的关系。
以往研究只在NP任务范式中发现了心理长度现象,同样经典的PN任务长期以来被忽略,缺乏指数表征到线性表征发展的实证研究(卢淳,郭红力,司继伟,孙燕,2014)。因此本研究关心儿童在PN估计任务中是否也会出现心理长度估计,并根据以往研究中对儿童出现心理长度估计的定义和检验,将儿童出现心理长度估计定义为:如果儿童在不同长度的数字线中对相同的长度估计相同,而对相同数字的估计存在差异则说明他们出现了心理长度估计,如在0~100数字线任务中,20cm数字线前1/100的位置到起点的长度(下文用20cm-1表示,以此类推)与10cm数字线前2/100的位置到起点的长度(下文用10cm-2表示,以此类推)相同,但20cm-1与10cm-1的长度不同;虽然20cm-1和10cm-1代表的真实值相同,但如果儿童出现心理长度估计,那么他们应该认为20cm-1和10cm-1代表的数值不同,而20cm-1和10cm-2代表了相同的数值。在PN任务中,如果儿童存在心理长度估计,那么较短的数字线任务应出现对数字的低估趋势,导致他们的表征模式符合指数表征。另外,很多研究发现学龄初期儿童的数字线表征发展变化较为明显(周广东等,2009),因此本研究选取7~9岁儿童作为被试,将探讨:(1)随着儿童年龄的增长,他们的心理长度如何变化;(2)心理长度的发展变化和表征模式变化的关系。
2 方法 2.1 被试
在某市的一所公立小学1~3年级三个班随机选取学生共109名,从学校的统计系统中调取儿童的精确出生日期和性别等信息。被试情况如表 1所示。
采用数字线估计范式中的PN任务。每个任务试次向被试呈现一条直线,直线的左右两端分别标有0和100,在每条直线上还会出现一条与该直线垂直的竖线,儿童需要判断竖线位置代表的数值为多少并将答案写在竖线上。参考前人选取的数字(韩瑽瑽,张静,黄大庆,陈英和,2010),将要求估计的数字定为21组,分别是:1~10、12、17、21、24、33、48、57、64、72、81、90,数字随机呈现。其中选取1~10是为了验证被试对10以内的数字是否出现心理长度估计,选取其他数字主要是为了区分线性和对数模型。实验分为两种条件,一种条件下的直线长度为20cm,另一种为10cm,两种条件出现的顺序按照ABBA法进行平衡。被试共需完成42个试次,每个试次都印在不同的答题纸上,最终形成了一个44页的数字线答题册。答题册的首页要求被试填写姓名和班级等信息,第2页为练习试次,即呈现一条标记中点位置的直线,要求儿童首先估计中点的数字。
2.3 程序
以班级为单位进行集体施测,采用纸笔测验法,向被试发放印有数字线估计任务的答题册,然后主试宣布指导语:“今天我们来玩一个小游戏,大家手中的答题册印了很多直线,直线上有一个竖线,请大家猜猜竖线走到了0~100中的哪个数字那里?请大家看第2页,这条线走到了0~100中间,它是多少?请把数字写在竖线上面。写完后你们再来猜猜后面的竖线走到了哪个数字,也把你的答案写在竖线上面。”这样,被试在正式实验前先完成一个练习,能在练习中正确写出50的被试才能进入数据分析,否则被试的数据将被剔除(所有儿童均通过练习)。主试告知儿童在实验过程中不能交流,不要用尺子量,要根据自己的感觉判断,结果不计入成绩。完成任务后主试给儿童一个小礼物表示感谢。
实验结果使用SPSS19.0软件进行统计分析,删除距离平均估计值上下三个标准差以外的估计值,20cm任务数据剔除率1.05%;10cm任务数据剔除率0.07%。 3 实验结果 3.1 儿童心理长度的发展特点分析
被试在10cm和20cm数字线中对1~10的估计均值如表 2所示,对其进行重复测量方差分析检验和多重比较,发现7岁被试存在心理长度估计,表现为被试在0~100数字线中对20cm-1至20cm-5的估计值与对10cm-1至10cm-5的估计值差异显著,但与对10cm-2、10cm-4、10cm-6、10cm-8、10cm-10的估计值差异不显著,由于20cm-1至20cm-5分别和10cm-2、10cm-4、10cm-6、10cm-8、10cm-10具有相同长度,这说明被试根据相同长度而非数量关系进行估计,出现心理长度估计。进一步分析发现,7岁儿童对10以上的数也存在心理长度,将儿童对20cm-12、10cm-12和10cm-24的估计值进行重复测量方差分析,结果发现组别的主效应显著F(2,31)=8.39,p<0.01,η2p=0.18,多重比较表明,7岁儿童对20cm-12的估计值(15.76±11.71)与对10cm-12的估计值(8.79±5.49)差异显著,F(2,31)=12.27,p<0.01,η2p=0.32;但他们对20cm-12的估计值与对10cm-24的估计值(16.00±11.37)差异不显著(p>0.05)。即当真实值同为12时,儿童在两种长度数字线中的估计值差异显著;但当需要估计的长度同为0.24cm时,儿童的估计值没有差异,出现心理长度估计,说明7岁儿童对超过10的数字也会使用心理长度而非根据数量关系进行估计。但7岁儿童心理长度的范围是有限的,他们对20cm-24的估计与对10cm-48的估计值有显著差异,t(31)=-2.70,p=0.01,cohen's d=0.48。
8岁儿童对1~4出现心理长度估计,但是他们对20cm-5的估计值与对10cm-5和10cm-10的估计值都有差异,即没有出现心理长度估计。进一步分析发现,8岁儿童对10以上的数字都没有出现心理长度估计。9岁儿童除了对20cm-2与对10cm-4的估计值没有差异外,在其他的比较中对相同长度的估计都有显著或者边缘显著的差异,说明到了9岁,儿童的心理长度基本消失。
| 年龄 | 真实值 | 组1. 20cm估计值 | 组2. 10cm估计值 | 真实值 | 组3. 10cm估计值 | 方差分析 | 组1-组 2多重比较 | 组1-组3多重比较 | |||
| F | η2p | F | η2p | F | η2p | ||||||
| 7 | 3.09±3.11 | 1.37±0.55 | 2.84±2.76 | 4.63** | 0.16 | 6.48** | 0.21 | 1.15 | 0.04 | ||
| 8 | 1 | 3.37±2.86 | 1.18±0.46 | 2 | 3.53±3.03 | 15.92** | 0.33 | 20.25** | 0.39 | 0.24 | 0.01 |
| 9 | 2.49±1.57 | 1.51±0.78 | 2.89±1.51 | 20.03** | 0.36 | 18.02** | 0.34 | 3.31b | 0.09 | ||
| 7 | 5.45±4.72 | 2.84±2.76 | 4.43±2.84 | 7.40** | 0.22 | 12.77* | 0.33 | 1.92 | 0.07 | ||
| 8 | 2 | 6.21±3.41 | 3.53±3.03 | 4 | 6.21±4.62 | 12.40** | 0.29 | 33.74** | 0.52 | 0 | 0 |
| 9 | 5.87±3.68 | 2.89±1.51 | 6.00±3.18 | 15.89** | 0.33 | 21.00** | 0.39 | 0.16 | 0.01 | ||
| 7 | 5.39±4.37 | 3.58±2.59 | 6.06±5.05 | 7.36** | 0.20 | 9.57** | 0.25 | 0.17 | 0.01 | ||
| 8 | 3 | 7.83±4.94 | 4.71±3.04 | 6 | 7.56±5.81 | 15.57** | 0.33 | 34.47** | 0.53 | 0.07 | 0 |
| 9 | 6.44±3.20 | 4.28±2.54 | 7.85±5.15 | 17.86** | 0.32 | 35.61** | 0.48 | 3.62b | 0.09 | ||
| 7 | 6.47±5.10 | 4.43±2.84 | 7.86±6.46 | 11.93** | 0.28 | 13.22** | 0.30 | 2.88 | 0.09 | ||
| 8 | 4 | 8.34±4.76 | 6.21±4.62 | 8 | 8.25±5.61 | 4.60* | 0.14 | 6.13** | 0.18 | 0.01 | 0 |
| 9 | 6.43±3.11 | 6.00±3.18 | 9.21±5.59 | 16.03** | 0.32 | 2.23 | 0.06 | 18.89** | 0.36 | ||
| 7 | 7.00±5.00 | 5.74±4.26 | 8.57±6.45 | 6.39** | 0.17 | 7.69** | 0.19 | 1.77 | 0.05 | ||
| 8 | 5 | 8.87±5.58 | 6.83±5.32 | 10 | 11.03±6.52 | 18.84** | 0.37 | 14.69** | 0.31 | 4.19* | 0.11 |
| 9 | 8.51±5.03 | 7.10±4.99 | 11.44±6.83 | 15.22** | 0.29 | 2.73 | 0.07 | 10.49* | 0.22 | ||
| 注:*表示p<0.05, **p<0.01,b表示边缘显著,0.05<p<0.1。 | |||||||||||
根据前人提出的数据处理方法,以各年龄组儿童对每个数字估计值的中数为因变量,以实际值为自变量进行线性和指数回归分析,并对两个函数的残差取绝对值进行差异检验(Siegler & Opfer,2003)。由于指数模型中的截距为1,因此对每个估计中值加1后进行回归分析。结果如表 3所示,对20cm数字线,儿童在7岁就出现线性表征趋势,7岁儿童组线性模型的解释率高于指数模型,且二者残差的差异达到边缘显著,t(20)=-1.80,p=0.08,cohen's d=0.40;随着儿童年龄的增大,两种模型的差异不断提高。但对10cm数字线,7岁儿童组的指数模型与线性模型残差差异不显著(p>0.05);结合图 1可以看出,7岁儿童对10cm数字线的表征仍带有指数模型的特征,对中点以下的数存在较为明显的低估现象;直到8岁,儿童的线性表征才显著优于指数表征,两种表征的差异显著,t(20)=-2.09,p=0.05,cohen's d=0.46;到9岁时,儿童线性表征的优势更为明显,t(20)=-2.28,p<0.05,cohen's d=0.50。
| 年龄组 | 20cm | 10cm | |||
| R2lin | R2exp | R2lin | R2exp | ||
| 7岁 | 0.99 | 0.92 | 0.97 | 0.93 | |
| 8岁 | 0.98 | 0.80 | 0.99 | 0.87 | |
| 9岁 | 0.99 | 0.83 | 0.99 | 0.84 | |
| 注:R2lin是线性表征的解释率, R2exp是指数表征的解释率。 | |||||
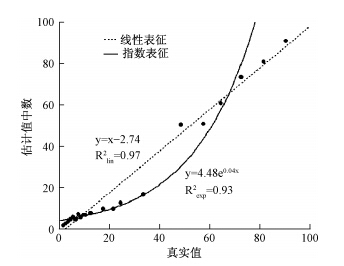 |
| 图 1 7岁儿童对10cm数字线估计的曲线拟合图 |
进一步对每名儿童的估计值进行线性和指数回归分析,删除距离平均值上下三个标准差以外的个体拟合数据(两种长度任务的剔除率均为7.34%),结果如表 4所示。根据以往研究的做法(卢淳等,2014),以数字线长度为被试内自变量,以年龄为被试间自变量,以线性表征解释率为因变量进行2×3混合因素方差分析检验,结果年龄的主效应显著,F(2,98)=17.66,p<0.01,η2p=0.27;年龄与数字线长度的交互作用显著,F(2,98)=6.77,p<0.01,η2p=0.12,对交互作用进行简单效应检验发现,7岁儿童的线性表征受到数字线长度的影响,F(2,98)=8.47,p<0.01,η2p=0.08,他们对20cm数字线的线性表征解释率高于10cm数字线;8岁儿童的线性表征也受到数字线长度的影响,F(2,98)=4.55,p<0.05,η2p=0.04,他们对10cm数字线的线性表征解释率高于20cm数字线;9岁儿童在两种长度任务上的线性表征没有显著差异(p>0.05)。
| 年龄组 | 20cm | 10cm | ||
| R2lin | R2exp | R2lin | R2exp | |
| 7岁 | 0.91±0.07 | 0.81±0.11 | 0.86±0.12 | 0.86±0.11 |
| 8岁 | 0.93±0.06 | 0.76±0.11 | 0.96±0.02 | 0.83±0.11 |
| 9岁 | 0.96±0.03 | 0.79±0.08 | 0.94±0.06 | 0.83±0.10 |
个体分析的另一种思路是比较线性模型占优势的人数比例,即比较R2lin> R2exp的儿童在年龄组中的所占比例(Xu,Chen,Pan,& Li,2013)。对20cm数字线,87.10%的7岁儿童,100%的8岁和9岁儿童线性表征优于指数表征;对10cm数字线,只有57.58%的7岁儿童线性表征优于指数表征,8、9岁组中则分别有94.11%和89.74%的儿童线性表征占优势。
3.3 儿童估计精确性的发展特点分析
儿童估计的精确性可用估计差异的绝对值(Absolute Error,AE)表示,AE=|估计值-实际值|。本研究中一名儿童的数据因超出平均值上下三个标准差被剔除,儿童最终在两种长度数字线中AE的描述统计结果如表 5所示。以数字线长度为被试内自变量、年龄为被试间自变量进行2×3混合因素方差分析检验,结果数字线长度的主效应不显著(p>0.05),儿童在10cm和20cm数字线中的估计精确性相似;年龄的主效应显著F(2,105)=14.27,p<0.01,η2p=0.21,数字线长度和年龄的交互作用也显著,F(2,105)=4.91,p=0.01,η2p=0.09,简单效应检验发现,只有8岁儿童在不同长度数字线估计任务中的AE有差异,F(2,105)=7.32,p<0.01,η2p=0.07,8岁儿童对10cm数字线估计的精确性显著高于20cm数字线,7、9岁儿童则没有这种差异(ps>0.05)。
| 年龄 | 20cm数字线 | 10cm数字线 |
| 7岁 | 8.68±4.90 | 9.68±5.46 |
| 8岁 | 6.73±3.76 | 5.07±2.44 |
| 9岁 | 5.21±2.78 | 5.39±2.32 |
本研究首次在数字线估计的PN任务中发现了儿童出现心理长度估计,说明不论数字与空间位置如何相互转换,儿童都会使用心理长度进行估计。本研究还发现7岁儿童对10以上的数也出现心理长度估计,超出了以往研究发现的1~10的范围。有研究者认为,对儿童来说,使用心理长度对10以内数字进行估计是较为简单的方法,而对更大的数字,由于数数和长度叠加的困难,叠加心理长度进行估计变得困难,儿童可能不再使用这种方法(莫雷等,2010)。但是,如果儿童已经累加心理长度到10,为什么他们不继续累加到11、12等与10相近的数呢?我们认为,造成儿童停止累加心理长度的一个可能的因素是出现了参照点,因为当真实值达到48以上(接近参照点50),7岁儿童的心理长度消失,这可能是因为中点对儿童的估计有提示作用,以往研究也证实,7岁儿童就能够使用中点帮助他们进行估计(Schneider et al., 2008);不过,考虑到儿童注意的持续性,本研究对10以上需要估计的数并没有连续取值,不能排除儿童在25~50的区间内停止累加心理长度的可能性。今后的研究可进一步增加在10~50区间内的需估计数字,探究7岁儿童出现心理长度估计的精确范围,并进一步确认8岁儿童对10附近的数字是否都不会使用心理长度估计,增加我们对心理长度发展规律的认识。
从心理长度范围的角度能较为准确地解释心理长度的发展趋势:7岁儿童对10以内,甚至10以上的数字使用心理长度估计,心理长度的范围较大;到了8岁,儿童心理长度的范围缩小到个位数;到了9岁,儿童的心理长度估计基本消失。这些结果说明随着儿童年龄的增长,他们的心理长度范围呈逐渐缩小而非突然消退的趋势。
4.2 儿童表征模式的发展及发展原因分析
我们从年龄组和个体水平对儿童表征模式的发展进行了分析。首先,从年龄组水平来说,本研究发现7岁儿童就能对20cm数字线进行线性表征,这与以往很多对中国儿童的研究结果一致(周广东等,2009; 潘茂明,2011)。但当数字线变为10cm时,7岁儿童线性和指数表征的差异不再显著,直到8岁,儿童在10cm数字线中的线性表征才明显优于指数表征,说明数字线长度会影响年幼儿童的表征模式。其次,个体拟合的结果发现7岁儿童对10cm数字线的线性表征解释率不及20cm数字线,8岁儿童则对10cm数字线的线性表征解释率更高。从个体线性比例占优势的人数比例也可看出,7~8岁时,儿童10cm数字线线性表征占优势的人数有了较大幅度的增长。
以上结果说明,儿童在7~8岁时出现心理长度估计且对10cm数字线的表征有较明显的发展变化,因此我们主要分析7、8岁儿童的心理长度与10cm数字线表征模式发展的关系。其中,8岁儿童虽然对多个10以内数字都存在心理长度估计,但不论年龄组水平还是个体水平的分析都发现他们对10cm数字线的线性表征解释率较高,说明对小数的心理长度估计难以影响表征模式。这个结果与莫雷等人(2010)的研究不一致,他们认为在数字线NP任务中,儿童对1~10的心理长度估计影响了估计的准确性,导致他们对这一范围内的数出现明显的高估,使表征模式在统计上符合对数模型。但是本研究结果提示了1~10在0~100数字线中仅占10%,对表征模式的影响是有限的,改变表征模式可能需要更大的数量范围或者包含一些关键值。有研究发现,能够改变表征模式的数量范围大于1~10,如Ebersbach等人(2008)用分段线性模型解释7岁儿童在0~100数字线估计任务中的估计值,发现分段线性模型的拐点为25,说明1~25范围内的数影响了7岁儿童的表征模式,这一范围大于1~10;Opfer和Siegler(2007)还发现在0~1000数字线中反馈儿童150的位置对改变儿童表征模式有很大影响。150在0~1000数字线上前15%的位置,本研究中7岁儿童在10cm数字线中出现心理长度估计的范围包含了这个位置,因此儿童对关键位置对应的数值可能存在低估,导致他们表征模式呈现非线性特征。总之,儿童对心理长度的累加可能必须达到一定的范围或者包含关键位置才能真正改变其表征模式。
根据本研究结果,我们认为,在数字线估计任务中,儿童表征模式从指数到线性模型变化的原因是,随着年龄增长,儿童心理长度的范围减小,导致他们低估的数字范围减小,不再出现指数表征的特征。心理长度本质上反映了儿童将数数策略应用于数字线估计中,因此它的消失可能提示了数数策略的消失,这一点与以往研究是相似的( vanViersen et al., 2013)。随着数学学习的深入,儿童开始学习除法知识,对部分和整体的关系有了新的认识,此后他们可能会更多地使用参照点策略进行估计,这导致了他们表征模式的变化(Link,Huber,Nuerk,& Moeller,2014)。总之,不同年龄儿童表征模式的差异可能来源于他们使用了不同的估计策略,而非源于表征本身的发展变化,多重表征理论在有关表征模式变化的观点上可能存在一定的缺陷。近期有研究者通过无边界数字线任务(unbounded number line task)测量了一至四年级及成人的数量表征。无边界任务只给出单位长度和线段起点,但不标注线段终点,要求被试根据单位长度判断数字的位置或者根据位置判断数字。结果发现,即使到了成人阶段,被试对无边界任务也不能进行线性表征,进一步反驳了多种表征理论中表征模式替换的观点(Link et al., 2014)。相比传统数字线任务,被试在无边界数字线任务中无法使用参照点策略,因此它能更“纯粹”地测量表征(Cohen & Blanc-Goldhammer,2011)。今后可比较中国儿童在有边界和无边界数字线任务中表征的差异,并探究其结果与其他数量表征任务(如数量比较任务)的关系,从而进一步确定何种数字线任务能更好地反映儿童真实的表征发展规律。
4.3 儿童数字线估计精确性的发展
本研究发现随着儿童年龄增长,其估计精确性不断提高,这与很多研究的结果一致(Siegler & Opfer,2003; 韩瑽瑽等,2010),也与儿童表征模式从非线性到线性的发展规律一致。本研究中,8岁儿童对10cm数字线的估计精确性高于20cm数字线,但由于7、9岁儿童的估计精确性并未受到数字线长度的影响,以往研究也并未关注长度对儿童表征精确性的影响,因此这一结果是否具有普遍性还需要进一步研究的证实。
本研究还发现,从年龄组水平上看,7岁儿童在不同长度数字线中的表征模式是不同的,从个体水平上看,他们的线性表征也受到数字线长度的影响;但是7岁儿童的表征精确性却没有受到数字线长度的影响。这可能是因为,表征模式是从整体上描绘了儿童的数量加工轮廓,而估计精确性则反映了对具体数量估计的准确程度。有研究也曾发现,虽然3~5岁的幼儿对0~100数字线均不能进行线性表征,但他们的表征精确性不同(Berteletti et al., 2010),也表现出了表征模式和精确性发展的分离。而且从线性和对数、指数函数的特征来看,这些函数都容易受到关键数字的影响,导致儿童出现不同的表征模式(Opfer & Siegler,2007);而估计的精确程度是依据个体所有的估计值算出的均值,不易受到个别数值的影响,因此虽然二者都是对数量精确加工的体现,但仍可能存在一些不同的发展规律。
5 结论
本研究通过设置10cm和20cm两种长度的数字线,对7~9岁儿童的数字线估计能力进行了测试,并得到以下主要结论:
(1)随着儿童年龄的增长,他们心理长度的范围逐渐缩小,7岁儿童对10以上的数存在心理长度,8岁儿童的心理长度在10以下,9岁儿童的心理长度基本消失;
(2)随着儿童年龄的增长,他们的数字线表征模式从非线性发展为线性,且儿童表征模式的发展与心理长度的范围逐渐缩小有关;
(3)随着年龄的增长,儿童的估计精确性不断提高,这与儿童表征模式的发展规律一致。
| Barth, H. C., & Paladino, A. M. (2011). The development of numerical estimation: evidence against a representational shift. Developmental Science, 14(1), 125-135. |
| Berteletti, I., Lucangeli, D., Piazza, M., Dehaene, S., & Zorzi, M. (2010). Numerical estimation in preschoolers. Developmental Psychology, 46(2), 545-551. |
| Booth, J. L., & Siegler, R. S. (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology, 41(6), 189-201. |
| Brysbaert, M. (2005). Number recognition in different formats. In: Campbell, J.I.D., Handbook of mathematical cognition (pp. 23-42). New York, NY: Psychology Press. |
| Cohen, D. J., & Blanc-Goldhammer, D. (2011). Numerical bias in bounded and unbounded number line tasks. Psychonomic Bulletin & Review , 18(2), 331-338. |
| Dehaene, S. (1997). The number sense: How the mind creates mathematics. New York: Oxford University Press, 53-76. |
| Ebersbach, M., Luwel, K., Frick, A., Onghena, P., & Verschaffel, L. (2008). The relationship between the shape of the mental number line and familiarity with numbers in 5-to 9-year old children: Evidence for a segmented linear model. Journal of Experimental Child Psychology, 99(1), 1-17. |
| Link, T., Huber, S., Nuerk, H., & Moeller, K. (2014). Unbounding the mental number line-new evidence on children's spatial representation of numbers. Frontiers in Psychology, 4, 1-12. |
| Moeller, K., Pixner, S., Kaufmann, L., & Nuerk, H. (2009). Children's early mental number line: Logarithmic or decomposed linear? Journal of Experimental Child Psychology, 103(4), 503-515. |
| Opfer, J. E., & Siegler, R. S. (2007). Representational change and children's numerical estimation. Cognitive Psychology, 55(3), 169-195. |
| Opfer, J. E., Siegler, R. S., & Young, C. J. (2011). The powers of noise-fitting: reply to Barth and Paladino. Developmental Science, 14(5), 1194-1204. |
| Schneider, M., Heine, A., Thaler, V., Torbeyns, J., De Smedt, B., & Verschaffel, L., et al. (2008). A validation of eye movements as a measure of elementary school children's developing number sense. Cognitive Development, 23(3), 409-422. |
| Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75(2), 428-444. |
| Siegler, R. S., & Mu, Y. (2008). Chinese children excel on novel mathematics problems even before elementary school. Psychological Science, 19(8), 759-763. |
| Siegler, R. S., & Opfer, J. E. (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science, 14(3), 237-250. |
| Slusser, E. B., Santiago, R. T., & Barth, H. C. (2013). Developmental change in numerical estimation. Journal of Experimental Psychology-General, 142(1), 193-208. |
| van Viersen, S., Slot, E. M., Kroesbergen, E. H., Van'T Noordende, J. E., & Leseman, P. P. M. (2013). The added value of eye-tracking in diagnosing dyscalculia: a case study. Frontiers in Psychology, 4(679), 1-13. |
| Xu, X., Chen, C., Pan, M., & Li, N. (2013). Development of numerical estimation in Chinese preschool children. Journal of Experimental Child Psychology, 116(2), 351-366. |
| 韩瑽瑽, 张静, 黄大庆, 陈英和. (2010). 2-4年级数学困难与普通儿童数量估计能力的比较. 中国特殊教育, (4), 47-51. |
| 卢淳, 郭红力, 司继伟, 孙燕. (2014). 不同数字线下儿童与成人分数估计的表征模式. 心理发展与教育, 30(5), 449-456. |
| 莫雷, 周广东, 温红博. (2010). 儿童数字估计的心理长度. 心理学报, 42(5), 569-580. |
| 潘茂明. (2011). 6-7岁儿童数字估计能力发展的追踪研究. 首都师范大学硕士学位论文. |
| 周广东, 莫雷, 温红博. (2009). 儿童数字估计的表征模式与发展. 心理发展与教育, 25(4), 21-29. |
 2015, Vol. 31
2015, Vol. 31


