国家教育部主管、北京师范大学主办。
文章信息
- 张睆, 辛自强. 2015.
- ZHANG Huan, XIN Ziqiang. 2015.
- 儿童表征深度的微观变化:路线、速度及来源
- The Micro-Change of Representational Depth: Path, Rate and Sources
- 心理发展与教育, 31(2): 137-148
- Acta Meteorologica Sinica, 31(2): 137-148.
- http://dx.doi.org/10.16187/j.cnki.issn1001-4918.2015.02.02
-
文章历史
2. 中央财经大学社会发展学院心理学系, 北京 100081
2. Department of Psychology at School of Social Development, Central University of Finance and Economics, Beijing 100081, China
在个体发展过程中,儿童需要不断地解决问题,而解决问题的关键在于对问题的成功表征,因而问题表征水平被视为儿童认知发展水平的重要体现。虽然衡量儿童问题表征水平的标准有很多,但成功表征问题的关键在于正确表征问题中所包含的关系(辛自强,2003)。可以说,儿童对问题中关系的表征能力,集中体现了儿童的问题表征水平。
辛自强提出的关系—表征复杂性模型为刻画儿童对问题中关系的表征能力提供了新的理论工具(辛自强,2007)。该理论认为,问题本身包含了一系列的集合(或要素)及其关系,这些集合关系的复杂程度称为问题的关系复杂性,它代表了问题本身的难度;而表征问题的关键则是理解这些集合关系,这种理解能力称为表征复杂性,它代表了儿童对问题的表征水平。表征复杂性包括表征广度和表征深度两个方面,表征广度指儿童所能理解的同一层次的关系数量,而表征深度指儿童能理解的关系的嵌套层次数量。所谓关系的嵌套,是指由于不同的关系在逻辑上前后相继而形成的逻辑层次,其中,高层次的关系是由低层次的关系相互关联而构成的,并且理解前者必须以理解后者为基础。例如,在太阳系中,太阳和月亮的关系是由“地球围绕太阳转”和“月亮围绕地球转”两个关系构成,且必须通过理解后两个关系才能推导出来。
与表征广度相比,表征深度更能体现儿童的问题表征水平。儿童在许多皮亚杰和新皮亚杰任务上的发展都可以视为表征深度的增加。皮亚杰的液体守恒任务即可说明,没有达到守恒水平的儿童只能在单一维度上比较两个事物大小,如液柱的高低或液面的宽窄,这时其表征深度为一级水平。那些达到守恒水平的儿童则可以将这两个维度统一起来综合考虑,这时其表征深度提高为二级水平(辛自强,2007)。
那么,表征深度是如何发展的呢?辛自强(Xin,2008)曾以小学四、五、六年级儿童为被试,以等级复杂性不同的一系列长方形面积问题为实验材料,考察了年级和任务复杂性对儿童问题表征的影响。结果表明,高年级儿童表征困难任务的能力要强于低年级儿童,任务越复杂这种优势越明显。其他相关研究在长方形面积问题(刘春晖,辛自强,2008)、数学应用题(辛自强,张莉,2009)、类比推理(张莉,辛自强,古丽扎伯克力,2010)、类推理(张丽,2008)等实验任务上也得到了类似发现。由于这些实验任务都仅有一种正确的表征方式,因此被试的表征深度即为其所能解决任务的等级复杂性。综合这些结果,可以认为儿童的表征深度随着年龄的发展而提高,尤其在小学四、五年级之间可能会发生较为显著的变化(刘春晖,辛自强,2008;辛自强,张莉,2009)。
虽然上述研究表明表征深度的发展是一个随年龄增长而单调上升的过程。但是,这种以年级为时间单位的横断研究只能从群体水平上说明表征深度的总体变化趋势,难以说明表征深度变化的发生过程及其机制。而观测密度更高的微观发生研究则可以更好地探讨这一问题。这一方面是因为,以年级(或年龄)为观测单位只能提供变化发生前后的信息,而微观发生研究要对正在发生的变化进行高密度的观测,可以提供关于变化发生过程的详尽信息,有利于回答变化是如何发生的(Siegler,2006;Siegler & Crowley,1991;辛自强,林崇德,2002)。另一方面,跨年龄的个体变化往往发生在日常生活背景之下,其中与变化有关的因素过于复杂,而微观发生研究中可以在特定的实验背景下对个体变化进行观测,有利于探讨变化发生的机制和影响因素(Lavelli et al., 2005;Siegler,2006)。基于此,本研究将着重探讨儿童表征深度的微观变化过程及其机制。
本研究将采用一种特殊的物理任务——齿轮推断任务来探讨这一问题。该任务由一组首尾相连的齿轮组成,其中一端的轮子为启动轮,另一端的轮子为目标轮,要求儿童根据启动轮的转动方向来推断目标轮的转动方向。由于这一任务并非提供一个真实的齿轮物理装置,而是呈现一幅描绘有齿轮装置的图片,这样儿童就不能通过转动启动轮而直接观察目标轮的转动方向,而必须首先要能正确表征启动轮和目标轮之间的关系,从而根据这一关系来推断目标轮的转动方向。
 |
| 图 1 齿轮推断任务 |
研究者可以根据儿童所遵循的推断规则来分析其表征到的齿轮间关系,以及这些关系之间的嵌套水平。以往研究表明,在齿轮推断任务上,儿童具有四种正确的推断规则(Dixon & Bangert,2002;Trudeau & Dixon,2007)。第一种是单步推断规则,他们根据上一齿轮的转动方向推论当前齿轮的转动方向,但是每次只能推断一步,其推断规则为“顺—逆,逆—顺”;第二种是连续推断规则,儿童可以进行连续的推断,其推断规则为“顺—逆—顺—逆”;第三种是跳跃推断规则,儿童可以根据第一个齿轮的转动方向直接推断第三个齿轮的转动方向并以此类推,其推断规则为“顺—顺—顺”;第四种为数学推断规则,儿童可以根据整组齿轮的数目是奇数还是偶数来做出推断,如果是奇数,则目标轮与启动轮转动方向相同,如果是偶数,则目标轮与启动轮转动方向相反,其推断规则为“奇数—相同,偶数—相反”。
据此,我们可以判断,儿童在齿轮推断任务上可能表现出多个层次的表征深度。如图 2所示,如果儿童采用的是单步推断规则或者连续推断规则,意味着他们仅仅理解了每两个相邻齿轮之间转动方向相反的关系,即相邻—相反关系。由于这一关系是齿轮之间最基本的关系,并没有嵌套任何其他关系,因此这时儿童的表征深度可定义为一级水平。如果儿童采用的是跳跃推断规则,则意味着他们认识到齿轮组中每间隔一个齿轮的两个齿轮之间转动方向相同,即相隔—相同关系。由于相隔—相同的关系是对相邻—相反关系再抽象的结果,或者说是由两个相反关系构成的一个相同关系,因此相隔—相同关系本身就嵌套了相邻—相反关系,这时儿童的表征深度为二级水平。如果儿童使用了数学推断规则,意味着他们理解了每两个齿轮可以组成一个单元,且所有单元的转动模式都是相同的,即多个相同关系关联在一起,还是相同关系,因此无须表征任何一个齿轮或单元的转动方向,只需要表征整个齿轮组的数目,并根据数目的奇偶判定目标轮的转动方向,即奇数相同—偶数相反关系。由于这一关系是从相隔—相同关系中抽象出来的,本身嵌套了相隔—相同关系以及相邻—相反关系,因此这时儿童的表征深度为三级水平。
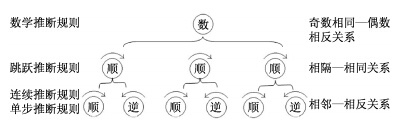 |
| 图 2 儿童在齿轮推断任务上可能的表征深度 |
本研究拟采用微观发生法探讨儿童在这种齿轮推断问题上表征深度的变化过程。相对于传统的横断设计,微观发生法可以对变化的过程和机制做出更好的分析。它基本的研究设计模式是在变化的关键期内对发生过程进行高密度的反复观测,并对观测结果进行精细的分析,以推断变化产生的原因,因而可以提供有关表征变化的详细信息(Siegler,2006;辛自强,林崇德,2002)。本研究将利用这一方法,从变化的路线、速度、来源三个角度对表征深度的变化过程与机制进行分析。
第一,从变化路线来看,表征深度发展的顺序如何?具体来说,儿童在表征深度的变化过程中,是否经历了从一级水平、二级水平再到三级水平的单调递增的变化过程?还是会存在多样的发展顺序甚至发展的倒退?这是关于表征深度变化的基本问题。回答这些问题不但可以帮助我们理解表征深度的发展顺序,而且可以为事前的表征深度分析提供实证检验。在本研究中,除了将整体分析被试群体的表征深度变化顺序,我们还将采用以个体为中心的分析思路,通过分析不同被试在6个实验期间中表征深度的变化顺序的个体间差异,来回答这些问题。
第二,表征深度的变化速度如何?这是关于表征深度变化的另一个基本问题。即使变化路线一定,表征深度也可能在不同发展阶段表现出不同的变化速度。所谓变化速度,即儿童在单位时间内的变化幅度。在本研究中,单位时间为一个实验期间,变化的幅度是被试群体在前后相邻期间处于各个表征深度的人数差异情况,它体现了被试群体在相邻期间表征深度的整体变化幅度。我们将通过分析儿童在前后相邻实验期间的表征深度的变化程度,来说明变化的速度。
第三,变化路线和速度都是对变化过程的描述,那么表征深度因何如此变化?或者说变化的来源是什么?这就需要对变化的机制和影响因素进行分析。
从变化机制上看,表征深度的增加,可以看做是个体对问题中所包含关系的更为抽象的理解或表征,而抽象知识的获得机制可能与个体对具体经验的反复表征有关。例如,皮亚杰很早就注意到重复的动作对于儿童获得数理逻辑知识的重要性,因此将图式称之为在动作中可以重复和概括的东西(皮亚杰,英海尔德,1981)。Karmiloff—Smith也认为,可灵活运用于多个领域的外显抽象知识,是在个体对特定领域的程序性知识进行反复表征的过程中产生的(Karmiloff—Smith,1992)。以往研究也表明,儿童对具体解题经验的重复表征,有利于其发现问题中所包含的抽象关系(Boncoddo,Dixon,& Kelley,2010;Dixon & Kelley,2007)。这都说明,表征深度变化机制可能与反复表征过程有密切关系。但是,也有观点认为,这种对单一具体经验的重复性表征并不利于抽象知识的获得,特别是如果被反复表征的练习任务是简单而难度相似的,那么这种反复表征将产生一个缺乏灵活性的,较为自动化的问题表征,从而使得表征转换变得更为困难(Helsdingen,Van Gog,& Van Merri nboer,2011a;Helsdingen,Van Gog,& Van Merrinboer,2011b;;Carlson & Yaure,1990;Goode,Geraci,& Roediger,2008)。
那么,对具体经验的反复表征能否促进个体问题表征深度的增加呢?在本研究中,我们让一组儿童进行多次齿轮推断任务的解决,并在每次任务完成后要求他们解释自己的解题过程。由于这种反复的练习和自我解释可以促使个体对当前任务进行反复表征(辛自强,张丽,林崇德,池丽萍,2006),我们假定,如果练习和自我解释次数会影响到表征深度的发展,那么就可以间接说明反复表征在表征深度发展中的作用。
从影响因素上看,表征深度的变化可能会受到练习模式的影响。以往研究表明,与包含单一任务的单一练习模式相比,包含多样化任务的混合练习模式会促进儿童对任务特征进行对比(Carlson & Yaure,1990;Helsdingen et al., 2011b;Rau,Aleven,& Rummel,2012),从而可能有利于儿童在低层次关系中抽象出高层次关系。
在本研究中,我们根据任务的难度将练习模式划分为单一和混合模式两种。单一练习模式中,所有任务全部由简单任务构成,而在混合练习模式下,我们在一系列简单练习任务中插入两个困难任务,由于简单任务和困难任务交错进行,因此称为混合练习模式。 其中,简单任务的中间齿轮数目均小于9,这样就使得儿童连续推断的次数基本不超出工作记忆的最大加工范围,而困难任务中间齿轮数目介于15~20个之间。
以往研究表明,在同一问题具有多种表征方式的条件下,个体对于问题的表征复杂性越高,解题步骤就越少(Zhang,Xin,Lin,& Li,2009),因此在任务难度增加的条件下,个体可能会通过努力增加对问题的表征深度,来找到更简捷的问题解决方法。因此我们预测,与仅仅包含简单任务的单一练习模式相比,包含了困难任务的混合练习模式更有利于表征深度的提高。
总之,本研究试图采用微观发生方法,从路线、速度和来源三个方面考察儿童在齿轮推断任务上的表征深度变化过程。我们假设:(1)反复的练习和自我解释可以促使个体对当前任务进行反复表征,而这种反复表征能促进个体问题表征深度的增加;(2)与仅包含简单任务的单一练习模式相比,包含困难任务的混合练习模式更有利于表征深度的增加。:此外,由于并不存在对变量间因果关系的推断问题,因而本研究对于表征深度变化过程的具体路线和速度不做假设而只如实描述。
2 研究方法 2.1 被试
以山西省太原市一所普通小学五年级三个班的68名儿童为被试,其中男生37名,女生31名。儿童的年龄在11岁~12岁之间,平均为11岁5个月。这些儿童色觉均正常。
2.2 实验模式
本实验采用微观发生设计(实验模式见表 1),具体包括单一和混合两种练习模式,每种模式包括6个实验期间。在全部6个实验期间中,期间1的作用主要考察被试的分组是否平衡,并用于筛除那些已经可以使用数学推断法则解决问题的被试,期间2到期间6则用于考察表征变化的特点(路线、速度)及其原因(变化的来源)。其中,期间3和期间5用于考察不同任务难度对表征变化的影响。
期间1测试结果表明,没有被试在期间1可以使用数学推断法则解决问题。所有68名儿童按照数学成绩、性别等特征匹配为两组。其中34人作为单一练习模式组,他们在每个实验期间始终接受2道简单任务;而另外34人作为混合练习模式组,他们在实验期间3和5分别接受困难任务,而在其余实验期间接受的是简单任务。
从研究逻辑来看,单一练习模式下,由于先后两次练习仅仅在练习和自我解释次数上存在差异,因此被试在相邻期间的表征深度变化,可以说明反复表征对表征深度的促进作用。
而与单一练习模式不同,混合练习模式在期间3和期间5分别插入了困难任务,此时,儿童在插入困难任务前后期间的表征深度差异,说明增加了一次困难任务练习导致的变化,而在单一练习模式下,相应期间的差异仅仅说明增加了一次简单任务导致的变化。通过这两种模式相应期间表征深度差异的对比,就可以推断任务难度对表征深度的促进作用。 2.3 实验材料
研究采用齿轮图作为实验材料。该图为一组首尾不相连的齿轮传动装置,要求儿童根据齿轮组中的启动轮的转动方向,判断目标轮的转动方向。其中启动轮、中间轮、目标轮分别用黑色、绿色和蓝色代表。整个齿轮组排列为有缺口的圆环形。由于该任务可以在不改变任务模式的情况下通过调整齿轮个数改变其任务难度,而且同一任务可以有多种表征方式,因此是微观发生研究较为理想的实验材料。
齿轮任务包括简单任务和困难任务两组。简单任务的中间轮数目为4~9个,而困难任务为15~20个。除任务难易之外,齿轮图共有包括启动轮转动方向(顺时针、逆时针)、中间轮数目性质(奇、偶)、中间轮数目(3种)、齿轮组缺口朝向(左上,右下)等4个特征维度,共24种特征组合。为保证每次呈现的齿轮图均不相同,每种特征组合设计一张相应的任务图片,因此共有简单任务24张,困难任务24张。在实验实施过程中,由计算机程序根据实验设计方案从两种任务中分别随机抽取。
研究者同时设计了6道奇偶数知识测试题。每道题目包括6个数字,个位数的两个,十位数的四个。其中三个奇数,三个偶数。例如:“3、8、14、17、22、41”。要求儿童分别挑出其中的奇数或偶数。只有被试能全部挑出正确的三个数字,方判定为正确解答该题,并计1分,否则计0分。测试时随机选出6道题目中的2道,因此奇偶数测试满分为2分。
整个实验采用E-prime2.0编制实验程序,另设计实验记录表用以记录被试的基本信息、奇偶数测题成绩以及在解决齿轮推断任务时的行为表现。同时,为了帮助儿童在实验前了解齿轮互相咬合转动的基本规律,研究者制作了一副由两个齿轮组成的齿轮模型。
2.4 实验程序
本研究由心理学专业的研究生担任主试进行个别施测收集数据。实验前首先对主试进行培训,以统一指导语以及一些意外情况的处理。
阶段一:实验准备与前测。
在此阶段,主试首先使用教具向儿童演示两个相互咬合齿轮的转动方式,并开始录音。接着,主试呈现三个分别为黑色、绿色和蓝色的相互独立的齿轮,并要求儿童指出它们的颜色,以判断儿童是否能正确识别启动轮(黑色)、目标轮(蓝色)和中间轮(绿色)。最后,呈现这三个相互咬合的齿轮,并询问儿童,当黑色轮顺时针转动时,绿色轮怎么转?蓝色轮又怎么转?以判断儿童是否掌握了齿轮咬合转动的基本方式,即相邻两个齿轮的转动方向相反。当儿童能正确回答绿色轮和蓝色轮转动方向后,才能进入正式实验。
阶段二:正式实验。
在正式实验前,向儿童宣读指导语:“小朋友你好! 我们现在来做个齿轮游戏。你可以使用任何方法来找到答案,确定答案后请你把你思考的过程详细说出来。”
整个正式实验包括6个实验期间,每个期间包括两次测试,整个实验共12次测试,所有儿童均参与了全部测试。每次测试大约2分钟,实验期间之间间隔30秒,整个实验大约持续30分钟。在每个测试中,主试首先呈现齿轮图,同时询问儿童黑色齿轮的转动方向,并记录结果,该问题用于测查儿童是否明确启动轮的转动方向;接着,主试询问儿童蓝色齿轮的转动方向,并记录答案;最后,主试询问儿童:“你是怎么想出答案的呢?请把你想的过程告诉老师”,在儿童报告完毕后,主试根据儿童是否判断正确评分,当儿童回答正确且使用了正确的解题策略(即基于上述四种正确推断规则解题),主试方可判定其答案为正确,同时将结果反馈给儿童。
阶段三:奇偶数知识测试。
由于数学推断规则涉及奇偶数知识,为确定被试儿童的奇偶数知识水平,所有儿童接受两道奇偶数测试题目。首先询问儿童:小朋友,你学过奇数和偶数么? 然后呈现测试题目:让儿童将其中的奇数或偶数挑出来。主试当场根据儿童的回答判定成绩。
2.5 资料编码
本研究需要对被试在解题过程中的口语报告资料进行编码。编码主要基于辛自强(2003)提出的关系—表征复杂性模型以及对齿轮推断任务的事前分析。根据这一理论,表征深度主要体现了儿童所理解的关系的嵌套层次。通过儿童口头报告的解题思路,研究者对其表征深度进行了编码,不同表征深度的操作定义及其口语报告举例见表 2,如果儿童不能正确解决问题,则说明他们未能正确表征齿轮任务中齿轮之间的关系,因此其表征深度为零级。
| 表征深度 | 定义 | 口语报告举例 |
| 零级水平 | 不能正确表征问题所中包含的关系 | 黑色齿轮与蓝色齿轮转动方向总是相反的,黑色齿轮顺时针,所以蓝色齿轮逆时针。 |
| 一级水平 | 可以正确表征齿轮转动的相邻—相反关系 | 一个一个数,黑色齿轮为逆时针,第一个绿色齿轮为顺时针,第二个绿色齿轮为顺时针,第三个绿色齿轮为逆时针……顺逆顺逆, |
| 二级水平 | 可以正确表征齿轮转动的相隔—相同关系 | 两个两个数,第一齿轮为顺时针,第三个顺时针,第五个顺时针…… |
| 三级水平 | 可以正确表征齿轮转动的奇数相同—偶数相反关系 | 中间如果隔双数,则相反。黑色齿轮为顺时针,一共有10个齿轮,10除以2等于5,是双数,(那么)蓝色齿轮为逆时针。 |
所有被试全部通过前测,并完成了6个实验期间共12次测试。我们描述了不同练习模式下儿童在每个实验期间达到不同表征深度的人数差异情况(表 3,图 3和图 4)。
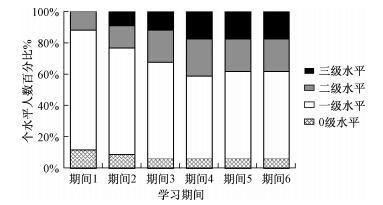 |
| 图 3 单一练习模式下儿童在每个期间达到不同表征深度的人数 |
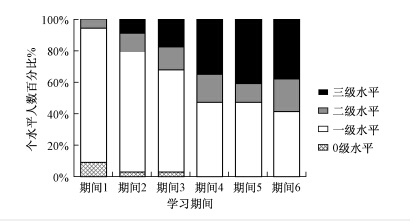 |
| 图 4 混合练习模式下儿童在每个期间达到不同表征深度的人数 |
| 零级水平 | 一级水平 | 二级水平 | 三级水平 | |||||
| n | % | n | % | n | % | n | % | |
| 单一练习模式 | ||||||||
| 期间1 | 4 | 11.76 | 26 | 76.48 | 4 | 11.76 | 0 | 0 |
| 期间2 | 3 | 8.82 | 23 | 67.65 | 5 | 14.71 | 3 | 8.82 |
| 期间3 | 2 | 5.88 | 21 | 61.76 | 7 | 20.59 | 4 | 11.76 |
| 期间4 | 2 | 5.88 | 18 | 52.94 | 8 | 23.53 | 6 | 17.65 |
| 期间5 | 2 | 5.88 | 19 | 55.89 | 7 | 20.59 | 6 | 17.65 |
| 期间6 | 3 | 8.82 | 18 | 52.95 | 7 | 20.59 | 6 | 17.65 |
| 混合练习模式 | ||||||||
| 期间1 | 3 | 8.82 | 29 | 85.29 | 2 | 5.88 | 0 | 0 |
| 期间2 | 1 | 2.94 | 26 | 76.47 | 4 | 11.76 | 3 | 8.82 |
| 期间3 | 1 | 2.94 | 22 | 64.71 | 5 | 14.70 | 6 | 17.65 |
| 期间4 | 0 | 0 | 16 | 47.06 | 6 | 17.65 | 12 | 35.29 |
| 期间5 | 0 | 0 | 16 | 47.06 | 4 | 11.76 | 14 | 41.18 |
| 期间6 | 0 | 0 | 14 | 41.18 | 7 | 20.59 | 13 | 38.23 |
从图 3和图 4中可以直观地看到,在两种练习模式下的各个期间中,处于零级水平的儿童数量始终很少,而处于一级表征水平的人数始终最多。同时,每个练习模式的不同期间中,处于一级表征深度的儿童有逐渐减少的趋势,处于三级表征水平的儿童则呈现逐渐增加的趋势。但是单一练习模式下这种变化趋势相对平缓,而在混合练习模式下,处于三级水平的儿童数量从期间3到期间4有一个非常明显的快速变化。
我们首先对不同组别儿童在期间1上的表征深度进行了非参数差异检验。曼特尼U检验结果表明,两组儿童的初始表征深度相同,Z=-0.27,p>0.05。我们同时检验了两组儿童在奇偶数知识上的差异。所有被试全部接受了奇偶数知识测试。单一练习模式下,M=1.38,SD=0.89,混合练习模式下,M=1.56,SD=0.75,结果表明两组儿童的奇偶数知识水平相同,t=-0.88,p>0.05。这说明两组被试奇偶数学知识水平以及实验开始时的表征深度在整体上基本相同。
从整体上讲,两组被试的表征深度是否发生了变化呢?分别对两种练习模式下各期间处于不同表征深度的人数进行非参数的相关样本整体差异检验(弗里德曼检验),结果表明,单一练习模式下,χ2(5,N=34)=26.99,p<0.001,混合练习模式下,χ2 (5,N=34)=68.59,p<0.001。这说明在两种练习模式下被试组都发生过表征深度的变化。那么,这种变化是否贯穿了整个实验期间?我们进一步检验了两组被试在期间6与期间1处于不同表征深度的人数差异情况,非参数的相关样本差异检验(维尔克松符号等级检验)结果表明,单一练习模式下Z=-2.80,p<0.01,混合练习模式下Z=-4.24,p<0.001。这一结果说明,从整个被试群体来看,无论在哪种练习模式下,儿童在整个实验期间上都发生了表征深度的变化,表现为一级水平的减少和三级水平的增加。
从整体上讲,不同练习模式是否会影响被试的表征深度变化?对于每个被试来说,其表征深度在期间6与期间1之间的差异体现了表征深度在整个实验期间的变化程度,因此我们将这一差异称为该被试表征深度在整个实验期间的变化幅度。分析不同组别被试的变化幅度差异,曼特尼U检验结果表明,Z=-2.40,p<0.05,说明被试表征深度的变化幅度在不同的练习模式间存在显著差异。另外,对每个期间两种练习模式下达到不同表征深度的儿童数量进行非参数差异检验。曼特尼U检验结果表明,期间6差异显著,Z6=-2.09,p<0.05,期间5差异接近显著,Z5=-1.85, p=0.06,其他期间之间差异不显著,Z1=-0.27,Z2=-0.187,Z3=-0.32,Z4=-1.52, ps>0.05。因此,从总体上看,不同的练习模式对于被试的表征深度的变化程度存在显著影响,并且这种影响在期间5和期间6上才有明显体现。
既然从整体上看,两种条件下都发生了表征深度的变化,而且不同的练习模式会影响到这种变化的程度,那么我们就有必要进一步对表征深度变化的路线、速度以及不同实验条件对它们的影响进行更精细的分析。
3.2 变化路线及其来源分析 3.2.1 不同练习模式下的表征变化路线
我们以单个被试为分析单位,分析了两种练习模式下68名被试在六个实验期间中表征深度的变化路线,具体参见图 5和图 6。圆圈内的数字表示被试在某实验期间表征深度的水平,横线上面或者下面的数字表示按此路线发生变化的人数。
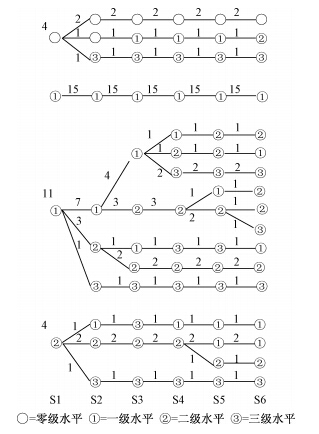 |
| 图 5 单一练习模式下儿童的表征变化路线 |
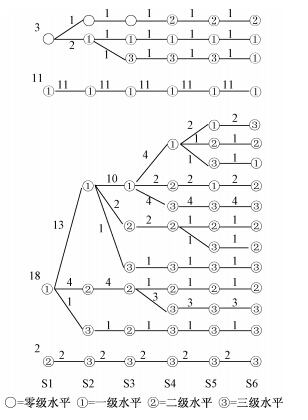 |
| 图 6 混合练习模式下儿童的表征变化路线 |
由图 5可见,单一练习模式下包括17条变化路线,表现为14种表征深度变化顺序:(1)从零级到一级水平到二级水平1人:(2)从零级水平直接到三级水平1人,(3)从一级水平发展到二级水平4人,(4)从一级水平到二级水平到三级水平1人,(5)从一级水平直接到三级水平3人,(6)从二级水平到三级水平1人,(7)从一级水平到二级水平再回到一级水平1人,(8)从二级水平到一级水平1人,(9)从一级水平到二级水平到一级水平到三级水平再到一级水平1人,(10)从二级水平到一级水平到三级水平再到一级水平1人,(11)从一级水平到二级水平到一级水平再回到二级水平1人,(12)始终为零级水平2人,(13)始终为1级水平15人,(14)始终为2级水平1人。
由图 6可见,混合练习模式下包括16条路线,表现为12种变化顺序:(1)零级水平到一级水平1人,(2)零级水平到二级水平1人,(3)一级水平到二级水平3人,(4)一级水平到二级水平到三级水平3人,(5)一级水平到三级水平 7人,(6)二级水平到三级水平2人,(7)零级水平到二级水平到三级水平回到一级水平1人,(8)一级水平到三级水平再回到一级水平1人,(9)一级水平到二级水平再回到一级水平再到二级水平2人,(10)一级水平到二级水平再到三级水平回到二级水平1人,(11)一级水平到三级水平再回到二级水平到三级水平1人,(12)始终保持在一级水平11人。
3.2.2 表征变化路线的模式
总体来看,这些变化路线可以概括为三大类变化模式:恒定不变、单调递增和循环波动。其中,在恒定不变模式下儿童的表征深度自始至终没有发生变化;在单调递增模式下,儿童的表征深度在整个实验期间发生了上升,而且后一期间总是高于或者等于前一个期间,整体上呈现单调递增的发展趋势;在循环波动模式下,儿童的表征深度在整个实验期间也发生了变化,但是这种变化不但包括上升,也包括下降,从而整体上呈现一个波动变化的趋势。统计结果表明,在全部68名被试中,28人为单调上升模式,11人为循环波动模式。有29人为恒定不变模式。
那么,在整个实验期间中,表征深度的发展是否遵循从低级水平向高级水平的变化路线?从变化的起点上看,在整个实验期间发生变化的39人中,期间1处于一级水平的有29人,占比74%,这说明变化主要是从最基本的一级水平开始发生的。从变化的模式来看,在所有发生变化的39人中,以单调递增方式变化的人数为28人,在循环波动模式11人中,波动上升的6人,水平波动的3人,而波动下降的只有2人,也就是说,在所有发生变化的个体中,总体呈现上升变化的有34人,占比87%。上述结果可以说明,当表征深度发生变化时,主要的发展模式是从最基本的一级水平向高级水平的递增过程,即儿童对高层次的数学关系的掌握是建立在对低层次的“相邻—相反”关系的理解基础上的。
在表征深度的发展路线中,也存在着少量的表征深度退步现象。在68名被试中,有11名被试至少出现一次退步,占整个群体的16%。在整个实验的340次变化中(每个被试经历5次变化),共发生了13次表征深度的退步,占全部变化的3.8%,同时,上升现象却发生了50次,维持现象发生了277次,上升和维持占全部变化的96.2%。这些结果也说明,在多个分析层次上,与表征深度的进步和维持相比,表征深度的退步都是较为少见的发展现象。
3.2.3 表征变化路线的来源
不同的练习模式对于表征发展路线的影响如何?分析结果表明,单一练习模式下,恒定18人,单调上升11人,波动5人,混合练习模式下,恒定11人,上升17人,波动6人。独立性χ2检验表明,不同练习模式下的变化模式之间差异不显著,χ2(2,N=68)=3.07,p>0.05。这说明,单一练习模式和混合练习模式下,表征深度的变化路线并没有表现出显著差异。同时,我们分析了不同练习模式下,能稳定停留在表征水平3上的人数是否不同。结果表明,对于在最后三个期间保持在表征水平3上的人数来说,单一练习模式下有5人,比率为15%,混合练习模式下有11 人,比率为31%。二者差异不显著,χ2(1,N=68)=26.99,p=0.086。
3.3 变化速度及其来源分析
儿童表征深度的变化是突然的还是渐进的?我们分别对两组被试在6个实验期间之间达到不同表征深度的人数情况进行相关样本的差异检验。维尔克松符号等级检验表明,单一练习模式下,只有期间1和期间2之间的差异接近显著,Z1-2=-1.93,p=0.05,其他各个相邻期间的差异均不显著,Z2-3=-1.67,Z3-4=-1.13,Z4-5=-0.58,Z5-6=0.00,ps>0.05。在非相邻期间中,期间二和期间四之间存在显著差异,Z2-4 =-2.64,p<0.01。混合练习模式下,期间1和期间2之间同样发生了显著变化,Z1-2=-2.89,p<0.01。除此以外,期间3和期间4之间发生了显著的变化,Z3-4=-2.74,p<0.01,期间2和期间3之间的变化也接近显著,Z2-3=-1.933,p=0.053,而其他相邻期间变化不显著,Z4-5 =-0.71,Z5-6 =-0.17,ps>0.05。
单一练习模式下,只有期间1与期间2之间的差异临界显著,这说明在期间1、2之间,儿童表征变化比较迅速。结合图 3可以看出,这期间达到三级水平的儿童增加,而保持在一级水平的儿童减少。由于先后两次练习仅仅在练习次数上存在差异,因此可以认为这种迅速的变化是由练习次数的增加引起的。此后,在期间3、4、5、6中,相邻期间儿童表征深度的差异不显著,但是在2、4之间的差异显著,说明连续两次练习依然可以引起表征深度的明显变化,只是与发生在相邻期间的变化相比,这种变化相对平缓。因此总的来看,单一练习模式下表征深度的变化速度,具有先快后慢的特点。
与单一练习模式相同,混合练习模式下,从期间1到期间2之间同样发生了表征深度的显著变化,由图 4可见,这种变化表现为一级水平的减少和三级水平的增加。这同样说明了在练习的初期,表征深度发生了迅速变化,而且这一变化是由练习次数增加所导致。
而与单一练习模式不同,混合练习模式在期间3插入了第一个困难练习。结果表明,从期间2到期间3,和从期间3到期间4上,儿童的表征深度都发生了迅速的变化,且变化表现为一级水平的减少和三级水平的增加。而在简单任务条件下,相应期间并没有发生显著的变化。这说明,期间3插入的困难任务可以引起表征深度的迅速变化。而且这一变化表现在两个方面。一方面体现在困难任务所处的期间中,即儿童在完成困难任务时,另一方面体现在完成困难任务后的下一期间中,或者说儿童在完成了困难任务之后。混合练习模式在期间5插入了第二个困难任务,结果表明,在期间4、5和期间5、6之间,儿童的表征深度变化不显著,总的来看,在混合练习模式下,表征深度的变化速度也体现出先快后慢的特点。
4 讨论
本研究采用微观发生法探讨了儿童解决齿轮推断任务过程中表征深度变化的路线、速度及其来源。综合上述研究结果,我们发现,在一个相对较短的时间尺度内,儿童的表征深度可以发生显著变化;从路线上看,这种变化主要体现为从低级水平向高级水平的递增过程,同时具有较大的个体间差异;而在速度上,表征深度的变化体现出先快后慢的特点。从来源上看,上述变化特点与练习与自我解释次数以及练习模式、任务难度等因素有关。下面我们将对这些结果分别进行讨论。
第一,表征深度的变化路线。从整个被试群体来看,两组被试在整个实验期间上都发生了表征深度的变化,处于一级表征深度的儿童逐渐减少,而处于三级表征深度的儿童逐渐增加。从变化模式的个体间差异来看,在表征深度发生变化的两组被试中,上升变化者都多于下降变化者;而从变化区间的分析来看,两种练习模式下进步的变化次数也均多于退步的变化次数。这些结果从多个层次上说明,无论是在单一还是在混合练习模式下,表征深度的微观变化都主要体现为从较低水平向较高水平的发展过程。这与表征深度的年龄变化相类似。张丽(2008)的研究即表明,对于 2~5年级儿童来说,随着年级的提高,他们对于类推理任务的表征深度呈现递增型的发展模式,即低表征深度的儿童逐渐减少,高表征深度的儿童逐渐增加。因此可以看出,无论在微观变化上,还是在年龄变化上,表征深度的发展都体现出了某种由低到高的顺序性特征。这也说明表征深度的确可以作为儿童问题表征能力发展的一项重要指标。
第二,表征深度的变化速度。本研究发现,无论在何种练习模式下,随着练习的进行,儿童表征深度的增加都表现出先快后慢的特点。事实上,先前关于表征的意识水平的微观发生研究中,也出现了表征水平变化先快后慢的现象(张丽,辛自强,2006)。对于这一现象的原因,我们将在最后部分加以讨论。
第三,表征深度的变化来源。表征深度的变化路线和速度实质上都是变化的具体表现,这些变化都有其原因或来源。
首先,表征深度的递增可能与练习和自我解释有关。研究结果表明,就整个被试群体来看,在单一练习模式下,被试在整个实验期间上都发生了表征深度的变化,表现为一级水平的减少和三级水平的增加。由于这些实验期间仅仅在练习和自我解释次数上有所不同,因此可以认为,练习和自我解释有助于表征深度的增加。这可能是由于反复的练习和自我解释会给儿童不断提供重新表征问题的机会(辛自强,张丽,林崇德,池丽萍,2006),而对同一表征的反复使用,会使得这种表征变得越来越容易激活和提取,利于个体从中抽象出更复杂的关系(Trudeau & Dixon,2007)。这支持了本研究的假设,即对具体经验的反复表征有助于问题表征深度的增加。
虽然从整体上看,反复表征确实促进了表征深度的发展,但是如果从个体的变化路线来看,反复表征的促进作用则具有明显的个体差异。在单一练习模式下的34名被试中,有接近一半(16名)被试在反复练习和自我解释的过程中,其表征深度出现变化,其中有15名在某些实验期间出现递增,这种变化可以归结于练习和自我解释的作用。与此同时,还有一半多(18名)被试维持恒定不变。也就是说,在对相邻—相反关系的反复表征过程中,这些被试表征虽然变得更容易激活和提取,但并没有从中产生新的、更高级的问题表征形式。这说明,虽然重复性练习与自我解释可促使被试进行反复表征,但这种反复表征仅仅能为表征深度的增加创造有利条件,而并不必然导致表征深度的发展。
其次,不同练习模式对于表征深度发展具有不同的促进作用。本研究结果表明,在混合练习模式下,儿童表征深度的变化幅度要高于单一练习模式。但在实验开始时,两组被试的表征深度以及相关数学知识水平在整体上基本相同,因而可以认为,两组儿童表征深度的最终差异应来自于两组采用了不同的练习模式。这一结果支持了本研究的假设。其原因可能在于,与单一练习模式不同,混合练习模式是由三个简单任务和两个困难任务混合而成,这种练习模式更有利于儿童对不同任务的解题过程进行对比(Carlson & Yaure,1990;Helsdingen et al., 2011;Rau et al., 2012),从而促进表征深度的发展。
最后,任务难度也可能会影响表征深度的增加。对于复杂练习组的被试来说,困难任务的第一次呈现引起表征深度的迅速变化,这可能是由于困难任务中包含了两倍于简单任务的齿轮数目,而当齿轮数量较大时,数学推断法则要优于其他法则。具体来说,当儿童使用数学推断法则时,他们仅需要数出整个齿轮组的数目就可以进行推断,数数对于五年级儿童来说,已经是一种高度熟练和自动化的技能(Rodríguez,Lago,Enesco,& Guerrero,2012)。而连续递推法则却需要以正反正反的方式来推断下一个齿轮的转动方向,这种推断方式对于儿童来说相对陌生,而且在工作记忆中循环的次数要多于数学推断法则,从而对儿童造成更高的认知负荷。已有研究表明,在儿童已学会使用某种表征解决问题的条件下,如果认知负荷过大,儿童会转换他们对问题的表征(Thevenot & Oakhill,2005;辛自强,张丽,2006)。因此齿轮较多的任务会迫使儿童表征问题中更深层次的关系,从而寻找一些更简洁的解题法则。
第一次困难任务完成之后,也引起了儿童表征深度的迅速变化。这可能与本研究采用的齿轮推断任务的特点有关。与有较少齿轮数目的简单任务相比,拥有更多齿轮数目的困难任务可以为推断策略的变化提供更多反复表征的“机会”。具体来讲,从连续推断策略到数学推断策略的变化过程中,对同一任务中各个齿轮转动方向的反复表征以及相互对比起着重要作用,而齿轮数目更长的任务显然可以提供更多的反复表征和对比的机会。因此完成困难任务之后,促进了部分儿童表征深度的变化。
本研究一个有趣的发现是,无论在哪种练习模式下,表征深度的变化速度都体现出先快后慢的特点。这可能意味着,虽然练习和自我解释次数以及任务难度都会影响到表征深度的发展,但这些因素对于表征深度变化的影响似乎有逐渐减弱的趋势。在单一练习模式下,随着练习和自我解释次数的增加,表征深度变化不断减慢。具体来说,在练习的初期,增加一次练习和自我解释就可以引起被试表征深度的显著变化,而随后则需要增加两次甚至多次才能引起类似的变化。这说明,在微观水平上,随着练习和自我解释次数的不断增加,能从这种反复表征中获益的被试越来越少,从而被试群体的表征深度变化越来越慢。在混合练习模式下,当我们在期间5插入了第二个困难练习时,发现期间4到5和期间5到6之间的差异均不显著。这一结果不同于在期间3插入第一个困难练习所导致的迅速变化。由此可见,与练习次数的作用相类似,任务难度对于表征变化的影响可能也存在递减的趋势。
为什么会有这种逐渐减弱的趋势呢?很可能是由于练习次数和难度等任务因素对表征深度发展的影响受到了个体思考积极性的调节。特别是在包含多次练习的微观发生研究中,个体这种积极性可能会随着练习的进行而逐渐减少,从而导致表征深度的变化呈现先快后慢的特点(辛自强,张丽,2006)。从本研究所获得的口语报告情况来看,在开始的几个测试期间询问儿童“你是怎么想到这个答案的”时,许多儿童会沉默一段时间,说明他们可能在进行一定的思考。而在随后的测试期间中,虽然练习以及自我解释提供了重复表征的机会,但是儿童并没有进行积极的重新思考,而是选择直接提取已有的答案。这时儿童在回答询问时,往往会迅速报告说“和刚才的(方法)一样”。
需要说明的是,由于研究实施过程中不具备录像条件,本研究未能对被试的推断规则进行多人独立编码,并报告相应的评分者信度。不过从口语报告录音来看,被试能够清晰地表达自己的推断法则,编码一致性未受到严重威胁。
虽然本研究结果表明,表征深度在微观尺度上和年龄尺度上具有相似的变化趋势,但是二者的变化来源,可能并非完全相同。年龄尺度上的表征深度变化,是在真实的日常情境中发生的,这一过程受到年龄阶段、知识经验、教育水平等多方面因素的影响,从而具有发展的性质。而在微观尺度上的表征深度变化,是在反复练习的背景下发生的。其变化受到了练习次数、练习模式以及任务难度等的影响,从而具有了学习的性质。因此,微观发生研究所得结论,并不能直接推论到年龄尺度的发展过程中(Karmiloff-Smith,2013)。本研究中,练习次数、任务难度等对表征发展的影响,实质上是说明了表征深度发展的一种微观学习机制。而年龄尺度的表征深度发展机制,则可能要复杂得多,需要在进一步研究中加以探讨。
5 结论
儿童的表征深度可以在微观尺度上发生显著变化。在变化路线上,表征深度的变化主要表现为从低向高的发展过程;在变化速度上,表征深度的变化表现出先快后慢的特点;在变化来源上,表征深度的变化与对具体经验的反复表征过程有关,并会受到练习模式和任务难度等因素的影响。
| Adolph, K. E., Robinson, S. R., Young, J. W., & Gill, A. F. (2008). What is the shape of developmental change? Psychological Review, 115, 527-543. |
| Boncoddo, R., Dixon, J. A., & Kelley, E. (2010). The emergence of a novel representation from action: evidence from preschoolers. Developmental Science, 13, 370-377. |
| Carlson, R. A., & Yaure, R. G. (1990). Practice schedules and the use of component skills in problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 16, 484-496. |
| Dixon, J. A., & Bangert, A. S. (2002). The prehistory of discovery: Precursors of representational change in solving gear system problems. Developmental Psychology, 38, 918-932. |
| Dixon, J. A., & Kelley, E. (2007). Theory revision and redescription. Current Directions in Psychological Science, 16(2), 111-115. |
| Goode, M. K., Geraci, L., & Roediger, H. L. (2008). Superiority of variable to repeated practice in transfer on anagram solution. Psychonomic Bulletin & Review, 15, 662-666. |
| Helsdingen, A. S., Van Gog, T., & Van Merrinboer, J. J. G. (2011a). The effects of practice schedule on learning a complex judgment task. Learning and Instruction, 21, 126-136. |
| Helsdingen, A. S., Van Gog, T., & Van Merrinboer, J. J. G. (2011b). The effects of practice schedule and critical thinking prompts on learning and transfer of a complex judgment task. Journal of Educational Psychology, 103, 383-398. |
| Karmiloff-Smith, A. (1992). Beyond modularity: A developmental perspective on cognitive science. Cambridge, MA: MIT Press. |
| Karmiloff-Smith, A. (2013).‘Microgenetics': No single method can elucidate human learning. Human Development, 56, 47-51. |
| Kotovsky, L., & Gentner, D. (1996). Comparison and categorization in the development of relational similarity. Child Development, 67, 2797-2822. |
| Lavelli, M., Pantoja, A., Hsu, H., Messinger, D., & Fogel, A. (2005). Using microgenetic designs to study change processes. In D. Teti (Ed.), Handbook of research methods in developmental science (pp. 40-65). Oxford, England: Blackwell. |
| Liu, C. H., & Xin, Z. Q. (2008). Relationship between the development of pupil's representation of area-of-rectangle problem and their fluid intelligence. Studies of Psychology and Behavior, 6(03), 206-211. |
| Piaget, J., & Inhelder, B. (1981). The Psychology of the Child (F. Y. Wu, Trans.).Beijing: The Commercial Press. |
| Rau, M. A., Aleven, V., & Rummel, N. (2012). Interleaved practice in multi-dimensional learning tasks: Which dimension should we interleave? Learning and Instruction, 23, 98-114. |
| Rodríguez, P., Lago, M. O., Enesco, I., & Guerrero, S. (2012). Children's understandings of counting: Detection of errors and pseudoerrors by kindergarten and primary school children. Journal of Experimental Child Psychology, 114, 35-46. |
| Schwartz, D. L., & Black, J. B. (1996). Shuttling between depictive models and abstract rules: Induction and fallback. Cognitive Science, 20, 457-497. |
| Siegler, R. S. (2004). U—shaped interest in U—shaped development—and what it means. Journal of Cognition and Development, 5, 1-10. |
| Siegler, R. S. (2006). Microgenetic analyses of learning. In W. Damon & R. M. Lerner (Series Eds.), & D. Kuhn & R. S. Siegler (Vol. Eds.), Handbook of child psychology: Vol 2: Cogniton, perception, and language (6th ed., pp. 464-510). Hoboken, NJ: Wiley |
| Siegler, R. S., & Crowley, K. (1991). The microgenetic method: A direct means for studying cognitive development. American Psychologist, 46, 606-620. |
| Thevenot, C., & Oakhill, J. (2005). The strategic use of alternative representations in arithmetic word problem solving. The Quarterly Journal of Experimental Psychology Section A: Human Experimental Psychology, 58, 1311-1323. |
| Trudeau, J. J., & Dixon, J. A. (2007). Embodiment and abstraction: Actions create relational representations. Psychonomic Bulletin and Review, 14, 994-1000. |
| Xin, Z. (2008). Fourth through sixth graders' representations of area-of-rectangle problems: Influences of relational complexity and cognitive holding power. The Journal of Psychology: Interdisciplinary and Applied, 142, 581-600. |
| Xin, Z. (2003). Validation of relational-representational complexity model. Acta Psychological Sinica, 35(4), 504-513. |
| Xin, Z. (2007). Relational-representational complexity model. Psychological Development and Education, 23(3), 122-128. |
| Xin, Z., & Lin, C. D. (2002). The microgenetic method: Focus on cognitive change. Advances in Psychological Science, 10(2), 206-212. |
| Xin, Z., & Zhang, L. (2009). Measuring students' representation level on arithmetic word problems: Based on the relational-representational complexity model. Psychological Development and Education, 25(1), 34-40. |
| Xin, Z., & Zhang, L. (2006). The change of representation and it's correlates: A microgenetic study. Acta Psychological Sinica, 38, 532-542. |
| Xin, Z., Zhang, L. Lin, C. D., & Chi, L. P. (2006). Change of Children's representational level in the context of practice. Acta Psychological Sinica, 38, 189-196. |
| Zhang, L. (2008). Children's representation on tasks with different complexities and the relationship between representation and working memory. Unpublished doctoral dissertation. Beijing Normal University. |
| Zhang, L., Xin, Z., Lin, C., & Li, H. (2009). The complexity of the Latin Square task and its influence on children's performance. Chinese Science Bulletin, 54, 766-775. |
| Zhang, L., Xin, Z. & Gulizha, B. (2010). The developmental characteristics of analogical reasoning on tasks with different complexity in 5-9 years old children. Psychological Development and Education, 26, 584-591. |
| 刘春晖, 辛自强. (2008). 小学生数学问题表征发展与流体智力的关系. 心理与行为研究, 6(03), 206-211. |
| 皮亚杰, 英海尔德. (1981). 儿童心理学(吴福元 译). 北京: 商务印书馆. |
| 辛自强 (2003). 关系-表征复杂性模型的检验. 心理学报, 35(4), 504-513. |
| 辛自强 (2007). 关系-表征复杂性模型. 心理发展与教育, 23(3), 122-128. |
| 辛自强, 林崇德. (2002). 微观发生法:聚焦认知变化. 心理科学进展, 10(2), 206-212. |
| 辛自强, 张莉. (2009). 基于关系-表征复杂性模型的数学应用题表征能力测验. 心理发展与教育, 25(1), 34-40. |
| 辛自强, 张丽. (2006). 表征变化及其影响因素的微观发生研究. 心理学报, 38, 532-542. |
| 辛自强, 张丽, 林崇德, 池丽萍. (2006). 练习背景下表征水平的变化. 心理学报, 38, 189-196. |
| 张丽. (2008). 儿童对复杂性不同任务的表征及其与工作记忆的关系. 北京师范大学.博士学位论文 |
| 张莉, 辛自强, 古丽扎伯克力. (2010). 5-9岁儿童在不同复杂性任务上类比推理的发展特点. 心理发展与教育, 26, 584-591. |
 2015, Vol. 31
2015, Vol. 31


