| 儿童青少年一般思维能力测验的编制和初步应用 |
2. 天津师范大学心理学部,天津 300387;
3. 国民心理健康评估与促进协同创新中心,天津 300387;
4. 北京师范大学发展心理研究院,北京 100875
思维是个体对客观事物概括和间接的认识。一般思维能力是儿童认知发展的核心能力,是批判性思维、创造性思维等高级思维能力的基础。
已有研究表明,一般思维能力与儿童的学业表现密切相关。例如,心理旋转和空间视觉化等形象思维能力与儿童的数学学习相关(Gilligan, Flouri, & Farran, 2017; 赖颖慧, 朱小爽, 黄大庆, 陈英和, 2014)。归纳推理与儿童语言学习中的语法、词汇习得及阅读理解均呈中等程度相关(Nikolov & Csapó, 2018)。传递性推理和条件推理等演绎推理能力分别与个体的数量表征和运算技能相关,且两者均与数学推理相关(Morsanyi, McCormack, & O’Mahony, 2018)。
纵向追踪研究发现,早期的一般思维能力可在一定程度上预测儿童之后的表现。儿童小学一年级时的空间能力可预测五年级时的几何和算数问题解决(Casey et al., 2015)。儿童12岁时的演绎推理能力可以预测15岁时在问题解决情境中的知识获得和知识应用情况(Greiff, et al., 2015)。
而且,对儿童一般思维能力的训练有助于提升其认知能力和相关的学业成就。例如,通过心理旋转任务训练可以提升6~8岁儿童在计算等数学任务中的表现(Cheng & Mix, 2014);类比推理的训练可以改进儿童的策略使用和言语解释,且可缩小工作记忆和语言对问题解决的影响(Resing, Bakker, Pronk, & Elliott, 2017)。
认识儿童青少年一般思维能力发展特点是思维培养的基础。林崇德(2006)认为思维是智力的核心成分,并在皮亚杰认知发展的经典理论基础上,提出了思维发展的新模式:思维从直观行动思维、具体形象思维到抽象逻辑思维的发展过程中,还伴随着动作逻辑思维和形象逻辑思维的发展。形象思维是以形象性的观念作为基本形式的思维,其主要心理成分有表象、联想和想象。形象思维的初级形态为具体形象思维,即以具体表象为材料的思维。随着年龄的增长,儿童逐渐产生形象逻辑思维。形象逻辑思维的载体仍然是具体、鲜明的形象,思维过程却有着高度的概括性。此后,儿童发展出基于抽象概念的逻辑思维。抽象逻辑思维包括形式逻辑思维和辩证逻辑思维。前者是正确地掌握概念并运用概念形成恰当的判断和合乎逻辑的推理。后者是高等逻辑思维,是人脑对客观事物的辩证关系的反映。
目前,我国关于儿童青少年思维发展的基本数据和现状资料仍然存在缺失。已有的研究大多关注思维个别方面的发展,如视知觉−空间表征(蔡华俭, 陈权, 2000; 施建农, 周林, 查子秀, 徐凡, 1997; 周珍, 连四清, 周春荔, 2005)、归纳推理(李红, 陈安涛, 冯廷勇, 李富洪, 龙长权, 2004)、类比推理(陈晓云, 1999)、演绎推理(巩子坤, 何卫国, 王海, 2013)。近期,《中国儿童青少年心理发育特征调查项目》选取了注意、记忆、视知觉−空间和推理能力作为认知能力发展的关键指标(董奇, 林崇德, 2011)等等。这些研究都从某些特定方面揭示了儿童青少年的思维发展特点,但均未从一般思维能力发展模式的视角,对具体形象思维、形象逻辑思维和抽象逻辑思维的发展模式和轨迹进行全面的描绘。
本研究作为“中国儿童青少年思维发展数据库建设及其发展模式的分析研究”课题的一部分,在以往研究的基础上,编制适宜我国5~18岁儿童青少年的一般思维能力测验,以期为数据库建设和后期研究提供有效工具。
2 一般思维能力测验编制 2.1 测验构想依据以往文献,5~18岁儿童青少年的思维发展中包括具体形象思维、形象逻辑思维、形式逻辑思维和辩证逻辑思维四种形式(林崇德, 2006)。
具体形象思维能力测验包括心理旋转测验和空间想象测验。心理旋转测验侧重于考察在二维或三维空间内对表象进行加工的能力。空间想象测验,采用图形折叠和图形展开想象任务,侧重于考察二维和三维空间之间的表象转化能力。
形象逻辑思维和形式逻辑思维均包括归纳推理和演绎推理两种典型推理形式。归纳推理是由特殊到一般的推理,从已经(或当前)观察到的现象推及未知现象的心理活动过程。演绎推理是由一般到特殊的推理,是在一般事实的基础上进行推理,从而得出某个正确的特殊结论。其中,形象逻辑推理以图形为内容载体,形式逻辑推理以数字和文字符号为载体。
辩证思维指的是个体能够联系、全面、发展地看待事物和思考问题。辩证逻辑判断往往表现为能够接受矛盾的认知倾向(刘书青, 彭凯平, 方平, 孟亦田, 林卓, 2013)。
2.2 初步编制测验本测验适合我国5~18岁儿童青少年的一般思维能力测验,便于大规模取样,能够以团体、纸笔形式,可在较短时间完成,兼顾各年龄阶段儿童并具有较好的鉴别力。首先,我们基于文献对测验的结构和内容进行论证,并组织领域内专家研讨,确定测验指标;其次,参考文献资料进行题目筛选、改编和编制,形成各个分测验的题库,组织专家评定测验题目的内容效度。再次,请小学、中学教师各20名对题目的可读性和可理解性进行评定。在此基础上对题目进行精选和修订,形成测验初稿,内容如下。
(1)表象。采用心理旋转测验,要求被试从四个选项中选出一个由靶图形平面旋转而来的图形。测试材料包括简笔画、字母和几何图形,共22道题目。
(2)空间想象。包括图形展开和图形折叠两种题型,分别要求被试从四个选项中选出立体靶图形的平面展开图形,或由平面靶图形折叠而成的立体图形,共32道题目。
(3)形象归纳推理要求被试从选项中选择可以填补在主题图缺失部分,使得整个图案合理完整的图片,共33道题目。
(4)形象演绎推理呈现N×N(2、3、4)的方格,要求每一行、每一列含有全部图形,且不重复,被试根据题目中给出的图形,推测出目标方格中的图形,共26道题目。
(5)抽象归纳推理包括数字序列和文字推理两种题型,共26道题目。数字序列题目呈现一列有规律的数字,要求被试根据数字间的规律选出恰当的选项;文字归纳推理要求被试根据提供的句子前提选出结论正确的选项。
(6)抽象演绎推理要求被试在给定句子前提下进行推理判断或给出结论,并选出相应的选项,共26道题目。
(7)辩证思维测验要求基于问题情境,对相关的解释进行判断,并选出相应的选项,共17道题目。
2.3 筛选题目 2.3.1 被试以整群方便取样的方式,在天津市市区普通中小学分别抽取二年级、五年级、初二年级、高二年级各八个班的学生对测验初稿进行预测。由于初测题目题量较大,为了控制测试时间并保证作答质量,将两个或三个分测验组合为题本,每个学生完成其中一个题本。由于儿童的辩证思维在中学阶段才开始发展,因此小学生不参加辩证思维分测验。各分测验的有效被试分布如表1所示。
| 表 1 一般思维能力测试第一次测验有效样本数(人) |
2.3.2 项目分析
对预测试的数据进行项目分析,删除或修改难度、区分度不合理的题目,并控制各测验的题目数量,最终形成正式测验。
首先,以每道题目的通过率为指标进行难度分析,删除难度系数大于0.9或小于0.1的题目。其次,利用题总相关和鉴别指数两个指标对预测试的题目进行项目区分度分析。由于希望保留部分难度较高或较低的题目,因此,仅删除各个题目与总测验的相关系数或高分组和低分组通过率的差值小于0.2的题目(骆方, 孟庆茂, 2005)。再次,为了控制测试时间,综合考虑难度和区分度,对保留的题目数量进行精简,每个分测验不超过10道题。在同等难度和区分度的题目中,优先考虑能够反映儿童思维发展性的题目。最终形成的正式测验包括:心理旋转、空间想象、形象归纳推理、形象演绎推理、抽象归纳推理、抽象演绎推理和辩证思维,共65道题目。
3 一般思维能力测验质量分析 3.1 被试以整群取样的方式,在天津市市区普通中小学抽取二年级、五年级、初二年级、高二年级的学生,进行一般思维能力测验正式测试,有效被试数为895名学生。随后,组织学生参加一般思维能力测验的重测和瑞文智力联合测验(效标测验),有效被试的整体情况如表2。
| 表 2 一般思维能力测验心理测量学指标分析有效样本分布表 |
3.2 施测过程
以纸笔形式进行整班的集体测试。由受过统一培训的心理学研究生担任主试,由学生本人在答题纸上作答。测验分段限时,严格要求学生按照时间完成相应部分的测试,不能随意翻页(往前或往后)。每个分测验,主试发出“开始”指令后,学生开始作答。主试发出“结束”指令后,学生马上停止作答。各分测验的施测流程均为:例题讲解,练习题及答疑,限时正式测试。心理旋转分测验限时为2分钟、空间想象分测验的限时为3分钟,其他分测验的限时为4分钟,包括指导语在内的总测试时间为45分钟左右。
3.3 项目分析首先,计算各分测验的题目得分率和平均得分率,以此作为难度的指标,得分率越高,说明难度越低,结果表明测验总体上难度适中,各分测验的题目难度分布和平均难度如表3所示。
| 表 3 一般思维能力测验项目分析(N=895) |
其次,计算各分测验题目的题总相关作为区分度的指标,相关越高,则区分度越好。结果表明,测验总体上区分度良好,个别难度较低或较高的题目上区分度略低。各分测验内题目的区分度分布亦见表3。
3.4 一般思维能力测验信度分析 3.4.1 内部一致性信度测验整体的克隆巴赫α系数为0.86,内部一致性信度好。除抽象演绎推理,其他各分测验均表现出较高的内部一致性信度,结果如表4所示。
| 表 4 一般思维能力测验信度 |
3.4.2 重测信度
重测信度是指用同一个测验对同一组被试施测两次所得测验分数的相关。重测信度较大说明前后两次测量的结果比较一致,测量工具比较稳定,所测量的被试心理特质受被试状态和环境变化的影响较小。
样本包括二年级、五年级、初二年级和高二年级共402名学生,两次测验之间间隔为3周左右,结果如表5所示,一般思维能力测验在各个年龄段均表现出较好的跨时间稳定性。
| 表 5 一般思维能力测验重测信度 |
3.5 一般思维能力测验效度分析 3.5.1 一般思维能力测验结构效度分析
根据测验编制的理论构想,使用Mplus8进行验证性因素分析。结果如表6所示,χ2/df<3,RMSA<0.08,CFI和TLI都在0.9以上,主要拟合指数符合心理测量的要求(温忠麟, 侯杰泰, 马什赫伯特, 2004),表明测验具有较好的结构效度。
| 表 6 一般思维能力测验的结构方程模型拟合指数 |
3.5.2 一般思维能力测验效标关联效度分析
考察测验是否有效预测与测验独立的效标行为,采用的效标主要有:学业成绩、瑞文智力测验联合型(CRT)。CRT测验的有效样本为二年级、五年级、初二年级和高二年级共527名学生,所有的被试都是先完成一般思维能力测验,间隔一周后完成CRT。学业成绩的指标为最近一次大型考试中的数学成绩,由中小学校的教务部门分别提供了五年级和初二年级的数据。结果如表7所示,在各个年龄段的学生中,一般思维能力测验与CRT和数学学业成绩之间均具有中等相关,表明其具有较好的效标效度。
| 表 7 一般思维能力测验效标效度 |
3.6 一般思维能力测验的初步应用
采用一般思维能力测验考察二年级、五年级、初二年级和高二年级学生在一般思维能力及其子维度的发展特点。为了更好地比较和呈现结果,计算各分测验均分并转化为百分制。如表8所示,儿童在一般思维能力测验及其分测验上的得分均随着年级上升而提高。
| 表 8 各年级学生一般思维能力的描述统计及差异分析(M±SD) |
进一步对各年级之间的测验得分差异进行统计分析发现,如图1所示,各分测验的得分随年级升高的变化表现出不一样的趋势。具体表现为:心理旋转,高二年级显著高于初二年级(p<0.001),五年级学生得分显著高于二年级(p<0.001),初二年级与五年级学生得分无显著差异;空间想象,初二年级显著高于五年级(p<0.001),五年级学生得分显著高于二年级(p<0.001),高二年级与初二年级学生得分无显著差异;形象归纳推理,高二年级显著高于初二年级(p<0.001),初二年级显著高于五年级(p<0.01),五年级学生得分显著高于二年级(p<0.001);形象演绎推理,初二年级显著高于五年级(p<0.001),五年级学生得分显著高于二年级(p<0.01),高二年级与初二年级学生得分无显著差异;抽象归纳推理,初二年级显著高于五年级(p<0.001),五年级学生得分显著高于二年级(p<0.001),高二年级与初二年级学生得分无显著差异;抽象演绎推理,高二年级显著高于初二年级(p<0.001),五年级学生得分显著高于二年级(p<0.001),初二年级与五年级学生得分无显著差异;辩证思维,高二年级显著高于初二年级(p<0.001)。
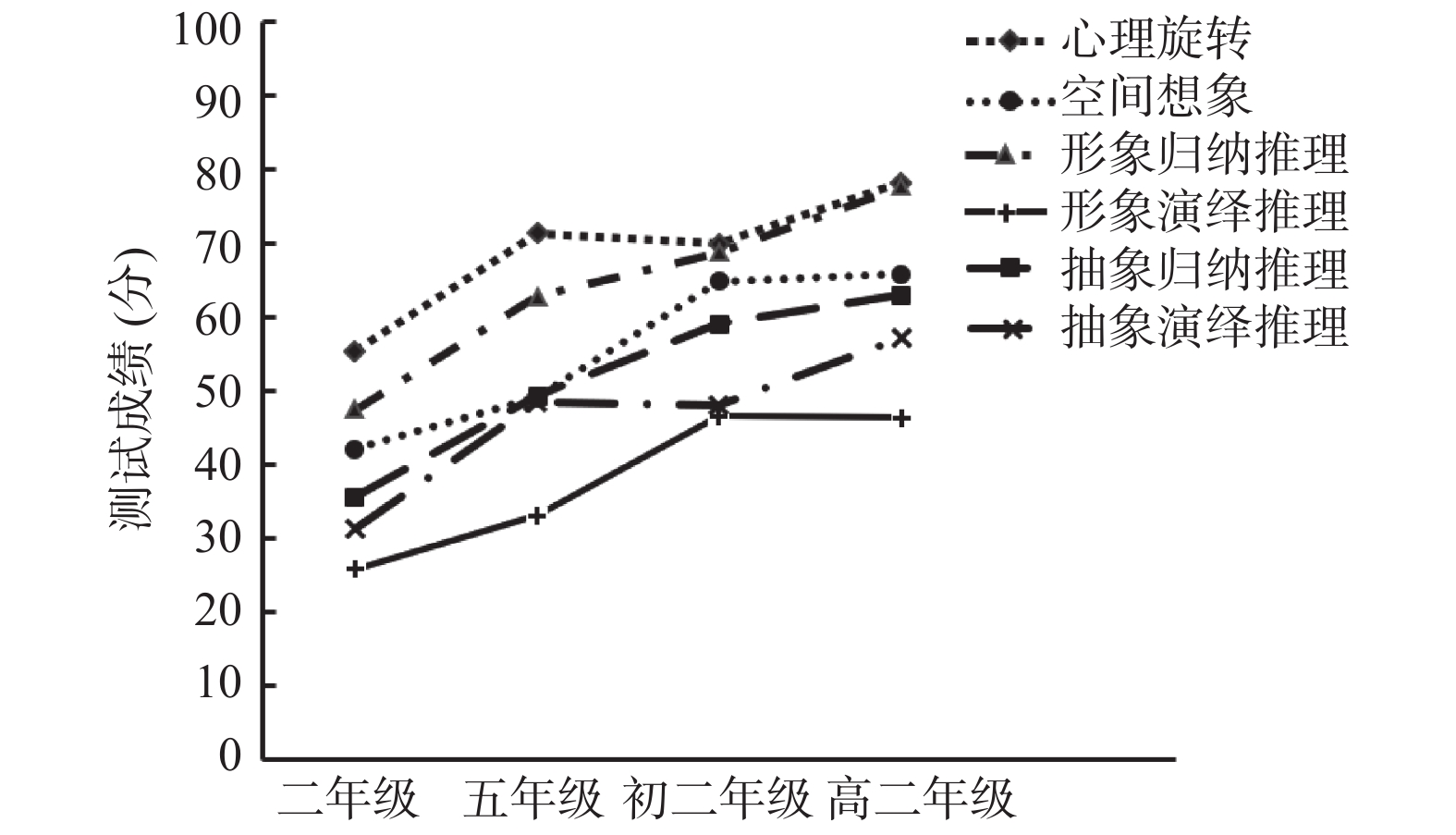 |
| 图 1 儿童一般思维发展趋势 |
4 讨论 4.1 一般思维能力的结构
皮亚杰提出的认知发展阶段理论认为,思维是单维发展途径,由直观思维到具体形象思维,再到抽象逻辑思维,高级思维逐级替代低级思维。而林崇德认为各种思维形式之间的关系并不是简单的替代关系,从而提出思维发展的新途径。个体思维的发展,不仅是前一级思维形式让位于后一级的思维形式,同时还表现为同一思维形式从低水平向高水平的发展(林崇德, 2006)。
本研究中,我们对儿童青少年一般思维能力发展的测查,对以往常用的形象思维和抽象思维的分类形式做了进一步区分,分别考察了具体形象思维、形象逻辑思维和抽象逻辑思维三种不同形式的思维。其中,形象逻辑思维在思维的材料和表征形式上基于感性形象,而在思维过程上则以逻辑推理的心理过程为主。对儿童一般思维能力发展的初步探查发现,形象演绎推理和抽象演绎推理先后进入发展期,而形象归纳推理能力在抽象归纳推理能力发展的同时仍一直保持上升的趋势,反映了思维的各种形式在发展过程中的替代与共存关系。
4.2 测验的质量在测验的编制和修订过程中,我们对题目进行了多次修改和筛选,最终确定的一般思维能力测验具有良好的心理测量学指标。总体来说,测验的难度适中。由于测查对象覆盖的年龄范围较广,所以在题目难度上酌情保留了一些难度较高或较低的题目,由此带来个别题目的区分度略低。
测验的信、效度指标大多符合心理测量学要求,测验具有较好地一致性信度和重测信度,以及较好的结构效度和效标效度。不足之处在于抽象演绎推理分测验的内部一致性信度偏低。这可能是由于抽象演绎推理本身涵盖的思维成分比较复杂。该分测验中包含了关系推理、条件推理和三段论推理等题目内容,因此内容一致性信度较低。在后续研究中,可考虑选取相对更具代表性的指标来测量演绎推理。
4.3 儿童青少年一般思维能力的发展特点本研究发现,从二年级(8岁)到五年级(11岁),一般思维能力的各个维度都在提高。这一研究结果与以往关于思维发展的相关调查结论大体上相似。中国儿童青少年心理发育特征调查项目报告中,以隐蔽图形任务和心理旋转任务作为视知觉−空间能力的测验任务,以数字类比测验、图形类比测验和图形序列测验作为推理能力的测验任务。该调查发现,6~15岁儿童青少年的视知觉−空间能力和推理能力在11岁之前稳步发展,11岁开始发展变缓(董奇, 林崇德, 2011)。这表明11岁之前,是一般思维能力发展迅速的阶段,也是一般思维能力培养的敏感期。
在五年级之后,一般思维能力的各维度仍在发展中,但分别表现出不同的发展模式。其中,形象归纳推理能力一直到高二年级都保持着上升趋势;心理旋转和抽象演绎推理是先经历一个平缓期,到初二年级再次进入发展期;而空间想象、形象演绎推理和抽象归纳推理则一直发展到初二年级,之后进入平缓期。如前所述,思维的发展包含两种路径,一是由低级思维形式转向高级思维形式,即思维表征形式从具体形象到抽象逻辑的转化;二是同一种思维形式从低水平到高水平的发展。各分维度思维能力的不同发展模式一方面可能是由于其背后核心的认知成分及其构成的差异,以及与儿童青少年大脑发育所带来的工作记忆、注意控制和抑制等能力的相关程度不同。另一方面,可能是各维度的思维能力对学习和经验知识的依赖程度不同。年幼儿童和年长儿童在完成同一种形式的思维任务时,涉及到的认知加工过程也可能有本质上的区别(Ricco, 2015)。因此,一般思维能力发展的内在心理机制以及各维度思维能力发展的具体模型有待更加精细和深入的研究。
本研究仅以天津地区的城市儿童青少年为被试,对其一般思维能力的发展特点和趋势进行了初步测查,验证了工具的有效性和可行性。对于我国儿童青少年一般思维能力发展全貌的描绘尚需更加科学的大规模抽样调查。
5 结论在本研究条件下,得出如下结论:(1)《儿童青少年一般思维能力测验》符合心理测量学要求,可作为儿童青少年一般思维能力的有效测量工具。(2)初步调查表明,儿童青少年的一般思维能力总体上随年龄增长而提高,各分维度表现出不同的发展模式。
蔡华俭, 陈权. (2000). 心理旋转能力的发展性及其与智力的相关性初步研究. 心理科学, 23(3): 363-365. DOI:10.3969/j.issn.1671-6981.2000.03.030 |
陈晓云. (1999). 10-14岁儿童几何图形推理能力的研究. 心理科学, 22(3): 267-268. |
董奇, 林崇德. (2011). 中国儿童青少年心理发育特征调查项目总报告. 北京: 科学出版社
|
巩子坤, 何卫国, 王海. (2013). 9~14岁儿童演绎推理认知与概率认知的相关性研究. 杭州师范大学学报(自然科学版), 12(3): 274-277, 283. DOI:10.3969/j.issn.1674-232X.2013.03.016 |
赖颖慧, 朱小爽, 黄大庆, 陈英和. (2014). 3-6年级数学学习困难儿童与正常儿童空间能力的比较. 心理与行为研究, 12(1): 36-44. DOI:10.3969/j.issn.1672-0628.2014.01.007 |
李红, 陈安涛, 冯廷勇, 李富洪, 龙长权. (2004). 个体归纳推理能力的发展及其机制研究展望. 心理科学, 27(6): 1457-1459. DOI:10.3969/j.issn.1671-6981.2004.06.049 |
林崇德. (2006). 思维心理学研究的几点回顾. 北京师范大学学报(社会科学版), (5): 35-42. DOI:10.3969/j.issn.1002-0209.2006.05.009 |
刘书青, 彭凯平, 方平, 孟亦田, 林卓. (2013). 辩证思维与辩证情绪的因果关系探究. 心理与行为研究, 11(4): 457-462. DOI:10.3969/j.issn.1672-0628.2013.04.005 |
骆方, 孟庆茂. (2005). 中学生创造性思维能力自评测验的编制. 心理发展与教育, 21(4): 94-98. DOI:10.3969/j.issn.1001-4918.2005.04.018 |
施建农, 周林, 查子秀, 徐凡. (1997). 儿童心理折叠能力的发展. 心理学报, 29(2): 160-165. |
温忠麟, 侯杰泰, 马什赫伯特. (2004). 结构方程模型检验: 拟合指数与卡方准则. 心理学报, 36(2): 186-194. |
周珍, 连四清, 周春荔. (2005). 中学生空间图形认知能力发展与数学成绩关系及其与智力的相关性研究. 数学教育学报, 14(1): 57-58, 94. DOI:10.3969/j.issn.1004-9894.2005.01.016 |
Casey, B. M., Pezaris, E., Fineman, B., Pollock, A., Demers, L., & Dearing, E. (2015). A longitudinal analysis of early spatial skills compared to arithmetic and verbal skills as predictors of fifth-grade girls' math reasoning. Learning and Individual Differences, 40: 90-100. DOI:10.1016/j.lindif.2015.03.028 |
Cheng, Y. L., & Mix, K. S. (2014). Spatial training improves children's mathematics ability. Journal of Cognition and Development, 15(1): 2-11. DOI:10.1080/15248372.2012.725186 |
Gilligan, K. A., Flouri, E., & Farran, E. K. (2017). The contribution of spatial ability to mathematics achievement in middle childhood. Journal of Experimental Child Psychology, 163: 107-125. DOI:10.1016/j.jecp.2017.04.016 |
Greiff, S., Wüstenberg, S., Goetz, T., Vainikainen, M. P., Hautamäki, J., & Bornstein, M. H. (2015). A longitudinal study of higher-order thinking skills: Working memory and fluid reasoning in childhood enhance complex problem solving in adolescence. Frontiers in Psychology, 6: 1060. |
Morsanyi, K., McCormack, T., & O'Mahony, E. (2018). The link between deductive reasoning and mathematics. Thinking & Reasoning, 24(2): 234-257. |
Nikolov, M., & Csapó, B. (2018). The relationships between 8th graders’ L1 and L2 reading skills, inductive reasoning and socio-economic status in early English and German as a foreign language programs. System, 73: 48-57. DOI:10.1016/j.system.2017.11.001 |
Resing, W. C. M., Bakker, M., Pronk, C. M. E., & Elliott, J. G. (2017). Progression paths in children’s problem solving: The influence of dynamic testing, initial variability, and working memory. Journal of Experimental Child Psychology, 153: 83-109. DOI:10.1016/j.jecp.2016.09.004 |
Ricco, R. B. (2015). The development of reasoning. In R. M. Lerner, L. S. Liben, & U. Mueller, (Eds.), Handbook of child psychology and developmental science (7th ed., Vol. 2, pp. 519-570). Hoboken, NJ: Wiley.
|
2. Faculty of Psychology, Tianjin Normal University, Tianjin 300387;
3. Center of Collaborative Innovation for Assessment and Promotion of Mental Health, Tianjin 300387;
4. Institute of Development Psychology, Beijing Normal University, Beijing 100875
 2019, Vol. 17
2019, Vol. 17


