| 速度与准确率权衡:被试反应状态评价与建模 |
反应时与准确率的关系是认知心理学的重要研究领域(Heitz, 2014; Ratcliff, Smith, Brown, & McKoon, 2016; Wickelgren, 1977)。在认知实验中,影响反应时与准确率关系的两个主要方面是认知能力或者信息加工效率(Wenger & Gibson, 2004; Wenger & Townsend, 2000)以及速度与准确率权衡(the speed-accuracy tradeoff, SAT; Donkin, Little, & Houpt, 2014; Ratcliff et al., 2016)。认知能力或信息加工效率越高,反应时越短,准确率越高;而速度与准确率权衡指被试有时会以牺牲准确率为代价换取加工速度,有时候会以牺牲加工速度为代价换取准确率提升(朱滢, 2009)。在行为实验中,速度一般用反应时作为指标,速度越快,反应时越短;反之,反应时越长。所以,认知实验的速度与准确率权衡就是反应时与准确率权衡。
在认知心理学中,研究被试的速度与准确率权衡通常以操作不同奖励措施或者反应时限制进行。这类研究在不同领域已有了大量的研究成果,特别是基于速度与准确率权衡模型(the speed-accuracy tradeoff model, SAT模型; Reed, 1973; Wickelgren, 1977)上进行的研究,如概念加工(McElree, Jia, & Litvak, 2000),句子理解(McElree, 2000; McElree, Foraker, & Dyer, 2003),记忆(McElree, 1998),注意(Giordano, McElree, & Carrasco, 2009; McElree & Carrasco, 1999)等领域。在不同实验条件下,通过对SAT模型中的参数组合进行变化,然后计算模型与数据拟合的R2指数(Reed, 1976),最后确定最佳的参数组合形式。这些研究发现SAT模型都能较好地拟合速度与准确率权衡数据(Reed, 1973; Wickelgren, 1977)。
SAT作为影响反应时与准确率关系的重要因素,不仅对认知实验有着重要的影响,在认知能力测验中也同样不可忽视(Goldhammer, Naumann, & Greiff, 2015; van der Linden, 2009; van der Maas, Molenaar, Maris, Kievit, & Borsboom, 2011)。认知能力测验的加工任务比认知实验任务更为复杂,通常也不会采用人为的实验控制(强调速度或者准确率,或者进行反应时限制)方法对SAT现象进行研究。在认知能力测验过程中,被试往往需要在有限的时间内完成测验作答,此时就需要在反应时与准确率之间进行权衡。这种权衡影响被试在项目上的作答反应时是否充足,进而对准确率产生不同的影响。
在认知能力测验中,对反应时与准确率联合分析的常用模型是van der Linden(2007)提出的分层模型。分层模型由两层构成,第一层为独立的反应时与反应模型,第二层是被试速度与能力的联合分布以及项目参数间的联合分布。分层模型仅通过被试能力与速度之间的相关来反映反应时与准确率的权衡关系。Meng,Tao和Chang(2015)用项目水平与被试水平的交互效应来解释反应时与准确率的关系,却无法反映反应时与准确率的动态权衡。Bolsinova,De Boeck和Tijmstra(2017)从项目水平角度,以残差反应时作为协变量引入反应模型中来反映反应时与准确率的权衡效应;Bolsinova,Tijmstra和Molenaar(2017)进一步扩展到被试水平,但是都过度扩大了反应时对准确率的影响。被试在项目上的作答准确率是能力与反应时双重作用的结果,能力决定了被试在项目上作答准确率的高度,而反应时则影响被试能否达到该准确率高度的重要因素。同时,Chen,De Boeck,Grady,Yanga和Waldschmidt(2018)通过作图发现,反应时与准确率在不同认知能力测验中并不是简单的单调递增关系,也有可能是先递增后递减的非单调趋势。
对于反应时与准确率的关系,认知实验通常认为随着反应时的增加,准确率是逐渐递增的,直到最高渐近线水平。但有的认知实验如再认实验,由于工作记忆的衰减和损耗,随着反应时的增加,会降低准确率。认知能力测验与认知实验的测试形式是明显不同的,并不存在学习效应,工作记忆衰减的影响较弱,这种递减趋势更可能受到项目难度、能力水平、速度水平或者能力与速度补偿效应的影响。基于此,本文结合认知实验SAT模型与分层模型,分别构建了基于能力水平、速度水平和速度与能力相互补偿的SAT分层模型,探讨认知能力测验中反应时与准确率的非单调关系。
2 SAT分层模型在SAT模型基础上,通过理论逻辑分析,并加入能力、速度以及能力与速度的补偿效应,构建三个SAT反应模型,使其能够反映能力、速度以及能力与速度补偿效应在反应时与准确率动态权衡关系中的作用,并联合反应时模型构成分层模型第一层;同时根据被试参数的联合分布与项目参数的联合分布构建分层模型的第二层,形成不同的SAT分层模型。
2.1 反应时模型在SAT分层模型中,反应时采用对数正态反应时模型(van der Linden, 2007),见公式1:
| $ {\rm{ln}}{{\rm{T}}_{{\rm{ij}}}} \sim {\rm{N}}\left( {{{{\text{β} }}_{\rm{j}}} - {{{\text{τ} }}_{\rm{i}}},{{\text{σ} }}_{\rm{j}}^2} \right){\rm{}} $ | (1) |
其中
Reed(1973, 1976)提出了反应时与准确率权衡关系的函数模型,见公式2:
| $ {\rm{d'}}({\rm{t}}) = {{\lambda }}*\left( {1 - \exp \left( { - {{\text{φ} }}*\left( {{\rm{t}} - {{\text{δ}}}} \right)} \right)} \right)\;\;\;\;{\rm{t}} > {{\text{δ} }}{\text{且}}{\rm{t}} \ne 0 $ | (2) |
在公式2中,
以能力水平的SAT反应模型为例,在认知能力测验情境下对公式2进行了重构。首先,
| $ {{\rm{\lambda }}_{{\rm{ij}}}} = {\rm{P}}\left( {{{\text{η}}_{{\rm{ij}}}} = 1|{{\text{θ}}_{\rm{i}}};{{\rm{a}}_{\rm{j}}},{{\rm{b}}_{\rm{j}}}} \right) = \frac{{\exp \left( {{{\rm{a}}_{\rm{j}}}{\rm{*}}\left( {{{\text{θ}}_{\rm{i}}} - {{\rm{b}}_{\rm{j}}}} \right)} \right)}}{{1 + \exp \left( {{{\rm{a}}_{\rm{j}}}{\rm{*}}\left( {{{\text{θ}}_{\rm{i}}} - {{\rm{b}}_{\rm{j}}}} \right)} \right)}} $ | (3) |
其次,对于
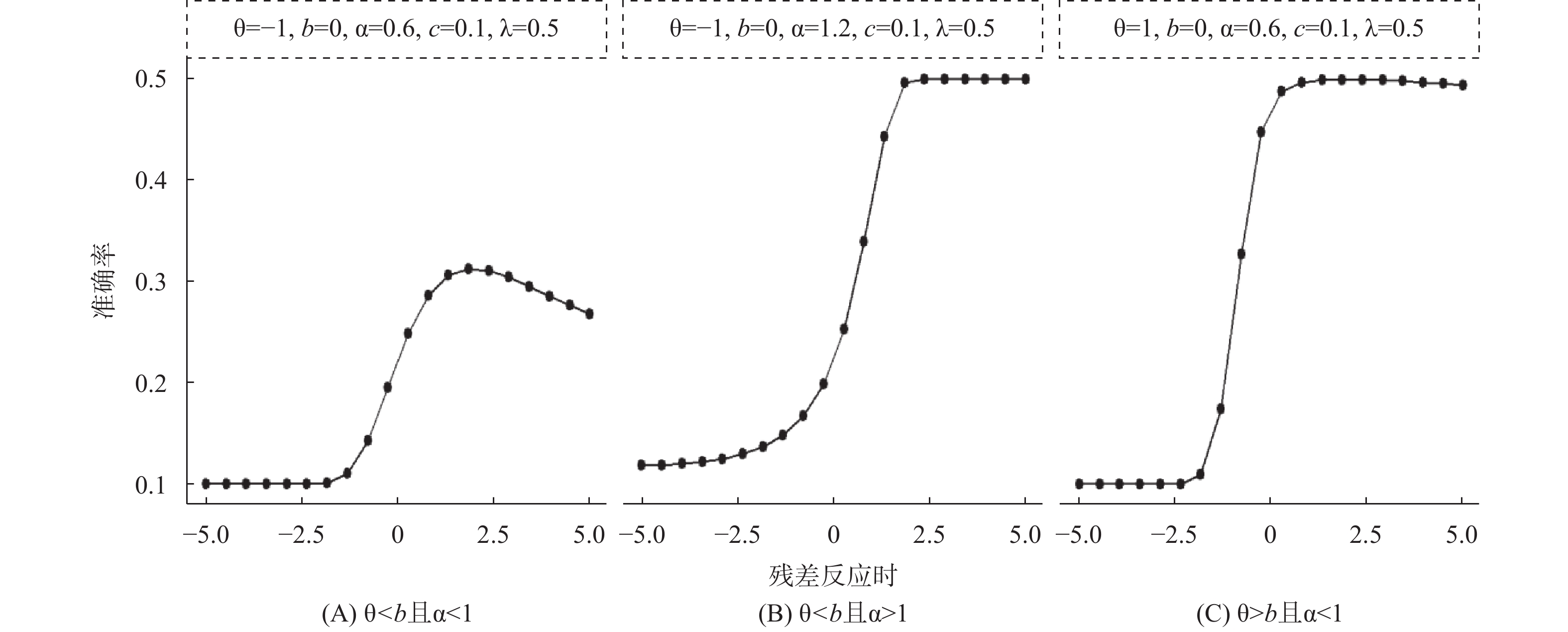 |
| 图 1 SAT-M1模型残差反应时与准确率关系 |
| $ {{\rm{Z}}_{{\rm{ij}}}} = \frac{{{\rm{ln}}{{\rm{T}}_{{\rm{ij}}}} - \left( {{{{\text{β} }}_{\rm{j}}} - {{\text{τ}}_{\rm{i}}}} \right)}}{{{{\text{σ}}_{\rm{j}}}}} $ | (4) |
| $ \begin{aligned} {\rm{P}}\left({{{\rm{X}}_{{\rm{ij}}}}} \right) =& 1|{{{\text{θ} }}_{\rm{i}}} = {{\rm{c}}_{\rm{j}}} + \left( {{{{\lambda }}_{{\rm{ij}}}} - {{\rm{c}}_{\rm{j}}}} \right){\rm{*}}\\ & \left( {1 - {\rm{exp}}\left( { - {\rm{exp}}\left( {{{{\text{θ} }}_{\rm{i}}} - {{\rm{b}}_{\rm{j}}} + {{\text{α} }}_{\rm{j}}^{{{\rm{Z}}_{{\rm{ij}}}}}{\rm{*}}{{\rm{Z}}_{{\rm{ij}}}}} \right)} \right)} \right) \end{aligned} $ | (5M1) |
依据SAT-M1构建的原理,同时构建了基于速度的SAT-M2模型(公式6, M2)和基于能力与速度补偿的SAT-M3模型(公式7, M3)。
| $ \begin{aligned} {\rm{P}}({{\rm{X}}_{{\rm{ij}}}} =& 1|{{{\text{θ}}}_{\rm{i}}}) = {{\rm{c}}_{\rm{j}}} + \left( {{{{\lambda }}_{{\rm{ij}}}} - {{\rm{c}}_{\rm{j}}}} \right){\rm{*}}\\ & \left( {1 - {\rm{exp}}\left( { - {\rm{exp}}\left( {{\text{τ}_{\rm{i}}} - {{{\text{β} }}_{\rm{j}}} + {{\text{α} }}_{\rm{j}}^{{{\rm{Z}}_{{\rm{ij}}}}}{\rm{*}}{{\rm{Z}}_{{\rm{ij}}}}} \right)} \right)} \right) \end{aligned} $ | (6M2) |
| $ \begin{aligned} {\rm{P}}({{\rm{X}}_{{\rm{ij}}}} =& 1|{{{\text{θ} }}_{\rm{i}}}) = {{\rm{c}}_{\rm{j}}} + \left( {{\lambda _{{\rm{ij}}}} - {{\rm{c}}_{\rm{j}}}} \right){\rm{*}}\Big( 1 - {\rm{exp}}\\ & {\left( { - {\rm{exp}}\left( {{{{\text{τ} }}_{\rm{i}}} - {{{ \text{β} }}_{\rm{j}}} + {{{\text{θ}}}_{\rm{i}}} - {{\rm{b}}_{\rm{j}}} + {{\text{α} }}_{\rm{j}}^{{{\rm{Z}}_{{\rm{ij}}}}}{\rm{*}}{{\rm{Z}}_{{\rm{ij}}}}} \right)} \right)} \Big) \end{aligned} $ | (7M3) |
上述三个反应模型是基于相同思路、不同的因素进行构建的。在不同项目上,反应时与准确率并不是独立的关系,被试的不同权衡状态会影响被试在项目上的作答反应时,进而影响被试在项目上的作答准确率。由于受到权衡状态的影响,项目的作答反应时与准确率并不总是单调关系,也可能存在非单调关系,同时非单调关系受到项目性质的影响。因此,在SAT-M1模型中,对工作量参数
在分层模型中,将对数正态反应时模型(公式1)与SAT-M1、SAT-M2和SAT-M3构成分层模型的第一层;能力参数与速度参数联合分布(公式8)以及各项目参数联合分布(公式9)构成分层模型的第二层。van der Linden分层模型(M0)则是将对数正态反应时模型与公式3(
| $ {{{\text{μ}}}_{\rm{I}}} = \left[ {{{\text{μ}}_{{\text{θ}}}}\;{{\text{μ}}_{{\text{τ} }}}} \right]{\text{与}}{{{\Sigma }}_{\rm{I}}} = \left[ {\begin{array}{*{20}{c}} {{{\text{σ}}}_{{\text{θ} }}^2}&{{{{\text{σ} }}_{{{\text{θ} \text{τ} }}}}}\\ {{{{\text{σ}}}_{{{\text{θ} \text{τ} }}}}}&{{{\text{σ} }}_{{\text{τ}}}^2} \end{array}} \right] $ | (8) |
| $ {{{\text{μ} }}_{\rm{J}}} = \left[ {{{{\text{μ} }}_{\rm{b}}}\;{{{\text{μ} }}_{{ \text{β}}}}} \right]{\text{与}}{{{\Sigma }}_{\rm{J}}} = \left[ {\begin{array}{*{20}{c}} {{{\text{σ} }}_{\rm{b}}^2}&{{{{\text{σ} }}_{{\rm{b }}\text{β}}}}\\ {{{{\text{σ} }}_{{\rm{b }}\text{β}}}}&{{{\text{σ} }}_{{\text{τ} }}^2} \end{array}} \right] $ | (9) |
为了能够对模型进行识别,需要对模型一些参数进行限制。在本研究中,对三个SAT分层模型的被试参数
对三个SAT分层模型所有参数,本文采用软件JAGS默认的Gibbs取样对被试与项目参数进行估计。在SAT分层模型中,各项目参数的先验分布分别为:aj,1/σj以及αj都服从大于0的左截尾正态分布N(0,1)I(0,),猜测参数cj为beta(5, 17)分布,项目参数bj与βj的均值向量μI服从二元正态分布,协方差矩阵ΣI服从逆威沙特分布InvWishart(R2,2),R2为二元对角矩阵。
对于被试参数,由于约束条件限定σθ2=1以及στ2=1,因此能力与速度参数的协方差与相关系数相等,即ρθτ=σθτ,并且ρθτ∈[–1, 1]。ρθτ的先验分布采用双侧截尾的正态分布ρθτ~N(0, 1)I(–1, 1)。
3.3 模型选择在选择拟合反应时与反应分层模型的最优模型时,以偏差信息准则DIC(Spiegelhalter, Best, Carlin, & van der Linde, 2002)作为评价四个模型拟合优劣指标。DIC值越小,说明该模型与实际数据拟合越好。
4 模拟研究 4.1 模拟设计为了检验建议模型参数的估计精度,对最复杂的SAT-M3模型进行模拟研究。各项目参数的生成分别为aj~N(0, 1)I(0,),
表1是项目参数的返真性。从表中可以看出,在被试量为500,测验长度为30时,与其他项目参数相比,α与a参数估计结果偏差,MSE值达到0.081和0.071,而其他项目参数都低于0.05。在被试量增加到1000时,α与a参数的MSE可以达到0.06以下,估计精度明显提高。所有项目参数Bias的绝对值都低于0.05,并且随着被试量增加,Bias绝对值普遍会有所降低。
| 表 1 分层模型项目参数MSE与Bias |
表2为被试参数估计结果。从表2可以看出,速度参数的MSE值一直低于0.03,而能力参数在测验长度从30增加到60时,MSE值从0.221减小到0.145,估计精度明显提高;能力与速度参数的偏差Bias都在0上下波动,绝对值不超过0.011。
| 表 2 被试参数MSE与Bias |
从上述模拟结果可以看出,SAT-M3分层模型的项目、被试参数通过MCMC算法得到有效的估计,而且随着被试量与测验长度的增加,估计精度会相应提高。
5 实例研究 5.1 数据描述本研究收集了被试在《瑞文标准推理测验》上的测试数据。数据采用E-prime1.0编写程序收集,计时从项目出现在显示器上开始到选择下一个项目停止,时间的记录单位为毫秒。被试选自两所县城高中的学生,测验长度为60个项目,控制测验最长作答时间为40分钟。施测340名被试,排除无效被试20人,有效被试320人。以van der Linden(2007)模型为基准模型(M0),加上本研究提出的模型共四个模型。在MCMC估计过程中,均使用n.chain=2条马尔科夫链,且包含n.iter=30000次迭代,燃烧次数n.burn=10000,稀疏值n.thin=2,最终剩余n.chain*(n.iter-n.burn)/n.thin=20000次迭代用于参数估计。参数拟合收敛采用潜在量尺缩减因子(potential scale reduction factor, PSRF; Brooks & Gelman, 1998),通常PSRF<1.1或1.2,本研究选择参数的PSRF均要求小于1.2来表示参数估计已经拟合。
5.2 研究结果四个模型数据拟合结果如表3,SAT-M3模型的DIC最小,其次SAT-M1模型,再次为SAT-M2模型,最大的是M0基准模型。根据DIC准则,SAT-M1与SAT-M2,都优于M0模型;而SAT-M1的拟合指数明显要小于SAT-M2,说明在项目上,反应时对准确率的影响更受被试能力水平的限制。同时,SAT-M3与SAT-M2相比,拟合优势并不明显,但是三个模型都比M0模型拟合更优,说明在考虑反应时对准确率的影响后,能明显提高模型对数据的拟合。
| 表 3 不同模型拟合指数 |
为了进一步分析SAT-M3模型,了解反应时与准确率关系,绘制了残差反应时区分度α与难度b以及项目工作量参数β的关系(如图2和图3所示)。在两图中,水平虚线分别为b和β的均值,而垂直虚线固定为1。从图2和图3可以看出,α均大于1的项目,除了一个项目外,其它项目难度均高于均值(第一象限),此时残差反应时与准确率关系是单调递增(图1-B)。在所有项目中,α参数大于1的项目有8个,小于1项目有52个,说明在大部分项目上,被试反应时与准确率存在两种不同类型:当能力水平低于项目难度时,被试的反应时对准确率影响为先增后减(图1-A),而当能力水平高于项目难度时,被试反应时与准确率关系为单调递增的曲线(图1-C)。
 |
| 图 2 α与b关系 |
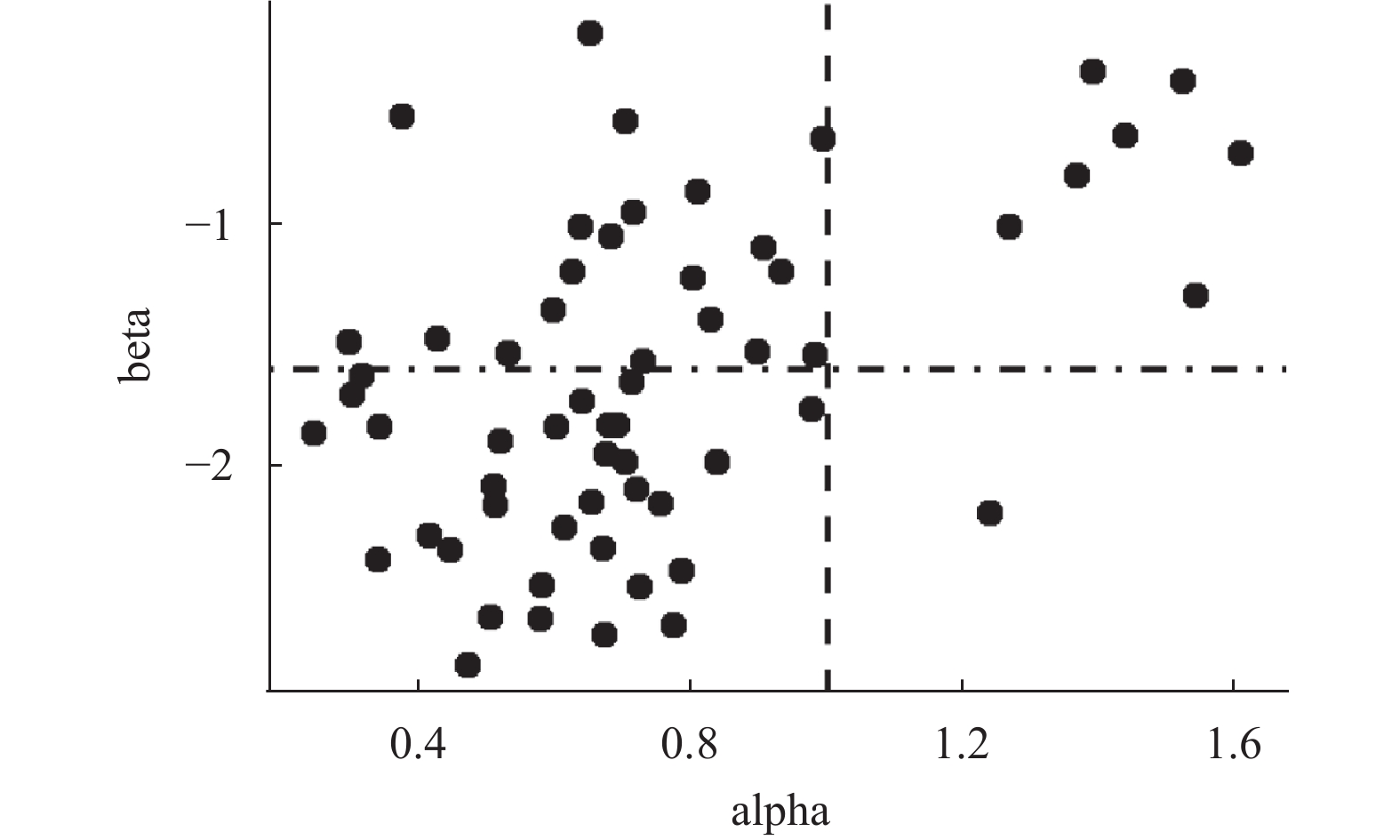 |
| 图 3 α与β关系 |
6 结论与展望
当前,反应与反应时数据的联合分析模式得到了迅速的发展,但是传统的分层模型并未深入考虑反应时与准确率的权衡。本文结合反应时与准确率权衡SAT模型与分层模型,对传统分层模型进行扩展,构建了能够反映反应时与准确率的不同关系的SAT分层模型。从模型拟合结果可以发现,考虑反应时对准确率不同影响关系能明显提高模型对数据的拟合。同时,根据实际数据的参数结果,不同被试在同一项目上的残差反应时与准确率的关系存在多种形式,并且这种形式是受到被试能力与项目难度多重影响的结果。
对三个SAT分层模型,SAT-M2模型可能由于仅考虑了速度的影响,拟合最差。在项目作答过程中,被试速度水平即使低于项目工作量参数,但是被试只要愿意花费足够反应时,可以弥补速度水平的不足,因此SAT-M2与M0在数据拟合上是趋近的,这也意味着测验时间基本充足。而在SAT-M1和SAT-M3上,被试能力水平的不足是无法通过增加反应时来弥补的,而且被试在作答过程中,一个符合逻辑的心理决策过程是高难度项目放弃或者快速作答,其观测反应时可能远低于期望反应时,必然会降低项目作答准确率;而对于简单项目,被试能力充足,在排除无关干扰下(失误等因素),作答反应时是否充足是影响准确率高低的唯一因素;最后对中等难度项目,被试更愿意消耗更多反应时,甚至远超期望反应时以提高准确率,但是受到能力水平影响,准确率增加到一定程度后,反而会降低,这种做题策略和心理与Wang和Zhang(2006)的研究结果相一致,却是van der Linden(2007)分层模型所忽视的。
当然有一些问题仍然有待进一步解决与完善。在SAT分层模型中,本研究选择的反应时模型是对数正态反应时模型,后续研究也可以比较对数偏正态模型(孟祥斌, 2016)以及其他的认知反应时模型(Anders, Alario, & van Maanen, 2016; Heathcote, 2004)的实际拟合结果。同时,在SAT分层模型中,反应时与准确率在认知能力测验项目上存在非单调关系,造成的原因除了项目难度以及能力等因素外,也可能与被试认知风格、人格等因素相关(Grigorenko & Sternberg, 1995; Kagan, Rosman, Day, Albert, & Phillips, 1964)。
孟祥斌. (2016). 项目反应时间的对数偏正态模型. 心理科学, 39(3): 727-734. |
朱滢. (2009). 实验心理学(第2版). 北京: 北京大学出版社.
|
Anders, R., Alario, F. X., & van Maanen, L. (2016). The shifted Wald distribution for response time data analysis. Psychological Methods, 21(3): 309-327. DOI:10.1037/met0000066 |
Bolsinova, M., De Boeck, P., & Tijmstra, J. (2017). Modelling conditional dependence between response time and accuracy. Psychometrika, 82(4): 1126-1148. DOI:10.1007/s11336-016-9537-6 |
Bolsinova, M., Tijmstra, J., & Molenaar, D. (2017). Response moderation models for conditional dependence between response time and response accuracy. British Journal of Mathematical and Statistical Psychology, 70(2): 257-279. DOI:10.1111/bmsp.12076 |
Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4): 434-455. |
Chen, H. Q., De Boeck, P., Gradya, M., Yanga, C. L., & Waldschmidta, D. (2018). Curvilinear dependency of response accuracy on response time in cognitive tests. Intelligence, 69: 16-23. DOI:10.1016/j.intell.2018.04.001 |
Donkin, C., Little, D. R., & Houpt, J. W. (2014). Assessing the speed-accuracy trade-off effect on the capacity of information processing. Journal of Experimental Psychology: Human Perception and Performance, 40(3): 1183-1202. DOI:10.1037/a0035947 |
Giordano, A. M., McElree, B., & Carrasco, M. (2009). On the automaticity and flexibility of covert attention: A speed-accuracy trade-off analysis. Journal of Vision, 9(3): 1-10. DOI:10.1167/9.3.1 |
Goldhammer, F., Naumann, J., & Greiff, S. (2015). More is not always better: The relation between item response and item response time in Raven's matrices. Journal of Intelligence, 3(1): 21-40. DOI:10.3390/jintelligence3010021 |
Grigorenko, E. L., & Sternberg, R. J. (1995). Thinking styles. In D. H. Saklofske & M. Zeidner (Eds.), Perspectives on individual differences. International handbook of personality and intelligence. New York: Plenum Press.
|
Heathcote, A. (2004). Fitting Wald and ex-Wald distributions to response time data: An example using functions for the S-PLUS package. Behavior Research Methods, Instruments, & Computers, 36(4): 678-694. |
Heitz, R. P. (2014). The speed-accuracy tradeoff: History, physiology, methodology, and behavior. Frontiers in Neuroscience, 8: 150. |
Kagan, J., Rosman, B. L., Day, D., Albert, J., & Phillips, W. (1964). Information processing in the child: Significance of analytic and reflective attitudes. Psychological Monographs: General and Applied, 78(1): 1-37. DOI:10.1037/h0093830 |
McElree, B. (1998). Attended and non-attended states in working memory: Accessing categorized structrures. Journal of Memory and Language, 38(2): 225-252. DOI:10.1006/jmla.1997.2545 |
McElree, B. (2000). Sentence comprehension is mediated by content-addressable memory structures. Journal of Psycholinguistic Research, 29(2): 111-123. DOI:10.1023/A:1005184709695 |
McElree, B., & Carrasco, M. (1999). The Temporal Dynamics of Visual Search: Evidence for Parallel Processing in Feature and Conjunction Searches. Journal of Experimental Psychology: Human Perception and Performance, 25(6): 1517-1539. DOI:10.1037/0096-1523.25.6.1517 |
McElree, B., Foraker, S., & Dyer, L. (2003). Memory structures that subserve sentence comprehension. Journal of Memory and Language, 48(1): 67-91. DOI:10.1016/S0749-596X(02)00515-6 |
McElree, B., Jia, G., & Litvak, A. (2000). the time course of conceptual processing in three bilingual populations. Journal of Memory and Language, 42(2): 229-254. DOI:10.1006/jmla.1999.2677 |
Meng, X. B., Tao, J., & Chang, H. H. (2015). A conditional joint modeling approach for locally dependent item responses and response times. Journal of Educational Measurement, 52(1): 1-27. DOI:10.1111/jedm.12060 |
Ratcliff, R., Smith, P. L., Brown, S. D., & McKoon, G. (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Sciences, 20(4): 260-281. DOI:10.1016/j.tics.2016.01.007 |
Reed, A. V. (1973). Speed-accuracy trade-off in recognition memory. Science, 181(4099): 574-576. DOI:10.1126/science.181.4099.574 |
Reed, A. V. (1976). List length and the time course of recognition in immediate memory. Memory & Cognition, 4(1): 16-30. |
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & van der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society. Series B, 64: 583-616. DOI:10.1111/1467-9868.00353 |
van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72(3): 287-308. DOI:10.1007/s11336-006-1478-z |
van der Linden, W. J. (2009). Conceptual issues in response-time modeling. Journal of Educational Measurement, 46(3): 247-272. DOI:10.1111/j.1745-3984.2009.00080.x |
van der Maas, H. L. J., Molenaar, D., Maris, G., Kievit, R., & Borsboom, D. (2011). Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychological Review, 118(2): 339-356. DOI:10.1037/a0022749 |
Wang, T. Y., & Zhang, J. W. (2006). Optimal partitioning of testing time: Theoretical properties and practical implications. Psychometrika, 71(1): 105-120. DOI:10.1007/s11336-002-1013-x |
Wenger, M. J., & Gibson, B. S. (2004). Using hazard functions to assess changes in processing capacity in an attentional cuing paradigm. Journal of Experimental Psychology: Human Perception and Performance, 30(4): 708-719. DOI:10.1037/0096-1523.30.4.708 |
Wenger, M. J., & Townsend, J. T. (2000). Basic response time tools for studying general processing capacity in attention, perception, and cognition. The Journal of General Psychology, 127(1): 67-99. DOI:10.1080/00221300009598571 |
Wickelgren, W. A. (1977). Speed-accuracy tradeoff and information processing dynamics. Acta Psychologica, 41(1): 67-85. DOI:10.1016/0001-6918(77)90012-9 |
 2019, Vol. 17
2019, Vol. 17


