| 发展性计算障碍儿童的数感缺陷 |
2. 中央财经大学社会与心理学院,北京 100081
发展性计算障碍(developmental dyscalculia, DD, 以下称计算障碍),是一种特殊的数学学习障碍。具体表现为发展性计算障碍儿童拥有正常水平的智力、稳定的情绪,同时具备适当的学习动机和良好的教育条件,但是他们在学习算术时仍然表现出困难,不能以正常的方式习得基本的算术(Mammarella, Hill, Devine, Caviola, & Szűcs, 2015; 白学军, 臧传丽, 2006)。虽然中国的学生在数学能力上相对较强,但调查研究发现我国仍有5%–6%的学生患有发展性计算障碍,与英国、美国、以色列、德国、瑞士等国调查的3%–6%的发生率基本一致(Shalev, 2004; 张树东, 董奇, 2007; 张怀英, 2009; 王芳, 路浩, 杨红, 赵晖, 2012; Di Filippo & Zoccolotti, 2018)。
以往有很多学者对发展性计算障碍的成因进行了探究,主要有“领域一般性”和“领域特异性”两种观点。其中近似数量系统假设是领域特异性的代表性理论之一。近似数量系统(approximate number system, ANS)是指个体在不需要依赖于计算和数量符号的情况下,对一组数量进行近似表征的系统(李红霞, 司继伟, 陈泽建, 张堂正, 2015)。Dehaene最早提出了该假设,他认为近似数量系统具有近似性和不精确性,并且不精确性随着数量的增加而增加(Dehaene, 1992)。近似数量系统遵循韦伯定律(Weber’s Law; Barth et al., 2006),其中韦伯分数越接近于0,表示近似表征越精确,近似数量系统的敏锐度越高。婴幼儿、儿童、成年人以及非人类的动物都具有近似数量表征能力(Kibbe & Feigenson, 2015)。概括来讲,近似数量系统的准确性通常使用数的敏感性(number acuity)或数感(number sense)能力来反映,使用非符号数量比较任务来测量(Bartelet, Vaessen, Blomert, & Ansari, 2014; Halberda, Mazzocco, & Feigenson, 2008; De Smedt, Noël, Gilmore, & Ansari, 2013)。非符号数量比较任务给被试呈现两个点阵列,每个点阵列中有一定数目的圆点,在不允许被试数数的前提下,让被试判断哪侧的数目较多,通过正确率、反应时或韦伯分数来衡量近似数量系统表征的精确性,即近似数量系统的敏锐度或数感能力。
基于近似数量系统假设,有研究者认为数感缺陷可能是发展性计算障碍产生的一个原因(Bugden & Ansari, 2016; Dehaene & Cohen, 1997; Piazza et al., 2010; Wilson & Dehaene, 2007; 张丽, 蒋慧, 赵立, 2018)。例如,Dehaene和Cohen(1997)认为发展性计算障碍患者存在数感缺陷,即不能快速理解、估计以及操纵非言语数字数量。Piazza等(2010)发现发展性计算障碍儿童的数感严重损伤,10岁计算障碍儿童的数感相当于正常儿童5岁的水平。Geary(2013)研究发现近似数量系统发育迟滞,即数感能力较差的儿童,存在数学学习困难。Bugden和Ansari(2016)对计算障碍儿童和正常儿童的数感能力进行比较,结果显示计算障碍儿童的韦伯分数要显著大于正常组儿童,表明计算障碍儿童存在数感缺陷。在2017年一篇元分析的文献中,Schwenk等(Schwenk et al., 2017)系统分析了过去关于计算障碍儿童数感能力的研究,发现计算障碍儿童的数感能力是显著低于正常儿童的。然而,也有一些研究发现计算障碍组被试和正常组被试之间在数感能力上并无差异(De Smedt & Gilmore, 2011; Szücs, Devine, Soltesz, Nobes, & Gabriel, 2013; Rousselle & Noël, 2007)。例如,Rousselle和Noёl(2007)使用阿拉伯数字和非符号数量比较任务对比了计算障碍儿童和正常组儿童之间的差异,结果发现计算障碍儿童在阿拉伯数字比较任务上存在缺陷,而在非符号数量任务上没有缺陷。De Smedt和Gilmore(2011)考察了一年级儿童的数量加工和估算能力,结果发现计算障碍组儿童在涉及符号信息提取的任务表现上与正常组儿童存在显著差异,表现出了加工缺陷,但是在非符号数量加工任务上与正常组儿童并没有显著差异。Szücs等(2013)亦没有发现障碍儿童和普通儿童在非符号比较任务上的成绩存在差异。
对已有研究进行深入剖析发现,不同研究之所以产生不同的研究结果可能有两个原因。首先,计算障碍儿童的筛选程序不统一。De Smedt和Gilmore(2011)的研究中,被试的筛选只选择了数学成绩的后25%一个标准,儿童的智力水平和阅读成绩都没有进行控制。其次,任务难度不同。Rousselle和Noёl(2007)的研究中的任务难度范围也只包括1:2和2:3。Szücs等(2013)研究中的难度范围也只有1:2,2:3和3:5,这对计算障碍儿童和正常儿童来说可能难度偏低,因而无法区分出其间差异。因此,与Szücs等(2013)筛选计算障碍儿童的程序类似,本研究采用了严格的标准,即计算障碍儿童的数学成绩排名在后25%,其智力水平和阅读成绩正常,而且统计分析中将智力水平作为协变量进行了控制。此外,本研究通过增大任务难度来考查以往研究结果的不一致是否和任务难度有关。以澄清计算障碍儿童是否存在数感缺陷这一问题。
如果计算障碍儿童存在数感缺陷,那么数感缺陷是否特定于计算障碍?阅读障碍是和计算障碍类似的一种发展性学习障碍。以往关于阅读障碍与计算障碍是否存在共病性存在争议。早期的主要观点是两种障碍存在特异性的缺陷(Landerl, Fussenegger, Moll, & Willurger, 2009; Rubinsten & Henik, 2006),即语音意识缺陷是阅读障碍的主要成因,而数感缺陷是计算障碍的主要成因。例如,Landerl等(2009)的研究发现计算障碍组只存在数感缺陷,而不存在语音意识缺陷,阅读障碍组只存在语音意识缺陷而不存在数感缺陷,阅读和计算双障碍组同时存在语音意识缺陷和数感缺陷。Träff,Desoete和Passolunghi(2017)的研究表明阅读障碍儿童在阿拉伯数字比较任务上的反应时长于正常组儿童,然而非符号数量比较任务(数感能力)上与正常组儿童并无差异。
然而,近年来越来越多的研究表明阅读障碍和计算障碍可能有一些共同的缺陷(De Smedt & Boets, 2010;Jordan, Wylie, & Mulhern, 2010;Peters, Bulthé, Daniels, Op de Beeck, & De Smedt, 2018;van der Stam, 2014)。De Smedt和Boets(2010)的研究发现有语音意识困难的阅读障碍儿童,其代数事实的提取存在困难。van der Stam(2014)的研究发现计算阅读双障碍组的语音意识不存在缺陷,但数字线表征存在缺陷。Peters等(2018)使用核磁技术发现阅读障碍,计算障碍和双障碍组被试在完成代数减法任务时的大脑激活模式非常相似。Willcutt等(2013)的研究则表明两种障碍既存在特异性的认知损伤,亦存在一般性的认知损伤,比如工作记忆,加工速度和言语理解。因此,与Landerl等(2009)和Träff等(2017)的研究类似,本研究亦拟探讨与正常儿童相比,阅读障碍以及双障碍儿童的数感能力是否较差。若回答是否定的,则说明数感缺陷是特异于计算障碍的;若回答是肯定的,则说明数感能力是阅读和计算障碍共同存在的一种缺陷。与Landerl等人的研究相比,为了更全面考查儿童的数感能力,本研究不仅分析了反应时数据,亦分析了正确率和韦伯分数。
综上,为了回答计算障碍儿童是否存在数感缺陷以及数感缺陷是否特定于计算障碍两个问题,本研究以计算障碍、阅读障碍、双障碍以及正常儿童为被试,以非符号数量比较任务,来考察计算障碍是否存在数感缺陷以及数感缺陷是否特异于计算障碍。
2 研究方法 2.1 研究对象选取重庆市内以及周边八所小学二三年级的学生参加被试筛选测验。第一步,对1696名学生施测了《中国儿童青少年数学学业成就测验》(内部一致性系数0.81)和《中国儿童青少年语文学业成就测验》(内部一致性系数为0.85)(董奇, 林崇德, 2011),按照年级将测验成绩转化为标准Z分数,以整体样本量的25%(Swanson & Beebe-Frankenberger, 2004)为临界点,选取数学成绩位于年级后25%,语文成绩在年级前75%的学生,筛选出296人确定为潜在计算障碍被试;在阅读障碍儿童筛选中,选取数学成绩位于年级前75%,语文成绩在年级后25%的学生,初步确定潜在阅读障碍组318人;在双障碍儿童筛选中,选取数学成绩位于年级后25%,语文成绩也在年级后25%的学生,确定潜在双障碍组210人。第二步,对第一步筛选出的被试施测瑞文智力测验(张厚粲, 王晓平, 1989),选取智力得分高于90分的学生,从而排除智力因素导致的学习障碍。同时请班主任对选取出来的学生进行客观评估,排除因其他原因(家庭环境、学习动机等)导致成绩较低的学生,最终确定计算障碍儿童72名,阅读障碍儿童76名,双障碍儿童69名。本研究中计算障碍儿童检出率(5.31%)和以往研究基本一致(王芳等, 2012; 张树东, 董奇, 2007)。从数学成绩和语文成绩都位于年级前75%的学生中,随机选取人数、年龄、智力相匹配的儿童作为正常组被试,并且同样通过班主任的评估,该组被试最终86人。
被试分为计算障碍组(72名, 平均年龄9.13岁, 男生40名, 占55.56%)、阅读障碍组(76名, 平均年龄9.20岁, 男生51人, 占67.11%)、双障碍组(69名, 平均年龄9.15岁, 男生54人, 占78.26%)和正常组(86名, 平均年龄9.07岁, 男生46名, 占53.49%),共计303名被试。
2.2 实验设计实验为4(组别: 数学障碍组, 阅读障碍组, 双障碍组, 正常组)×6(刺激比例: 1:2; 2:3; 3:4; 5:6; 6:7; 7:8)的混合设计,其中组别是组间变量,刺激比例为组内变量。
2.3 任务和程序非符号比较任务:该实验任务采用E-prime l.0进行编制呈现,见图1。实验材料为不同大小的黑色圆点,点数范围为5到16。为了保证数量大小不在感数范围内,排除感数的影响,选择点数大于4。不同数量的点阵列分别呈现在同一屏幕上的两个相同大小的方框中,要求被试根据感觉而不能数数来判断哪个方框中的点数较多,并且尽可能快的按下相应的键,“F”键表示左侧方框内的点阵数量大,“J”键表示右侧方框内的点阵数量大。实验材料会一直呈现,直到被试做出相关的按键反应以后点阵列才会消失。其中两个方框中的点数比例有以下六种:1:2;2:3;3:4;5:6;6:7;7:8。每种比例下有12个试次,所以正式实验共两个block每个block有36个试次,中间进行短时间的休息。正式实验开始前有10个试次的练习以及结果反馈。实验任务中一半试次点阵两侧点的总面积相等,一半试次点阵两侧点的平均面积相等,从而保证了无关因素对实验任务的影响(Dietrich, Huber, & Nuerk, 2015),且点数较多的方框左右出现的次数在实验中也进行了平衡。
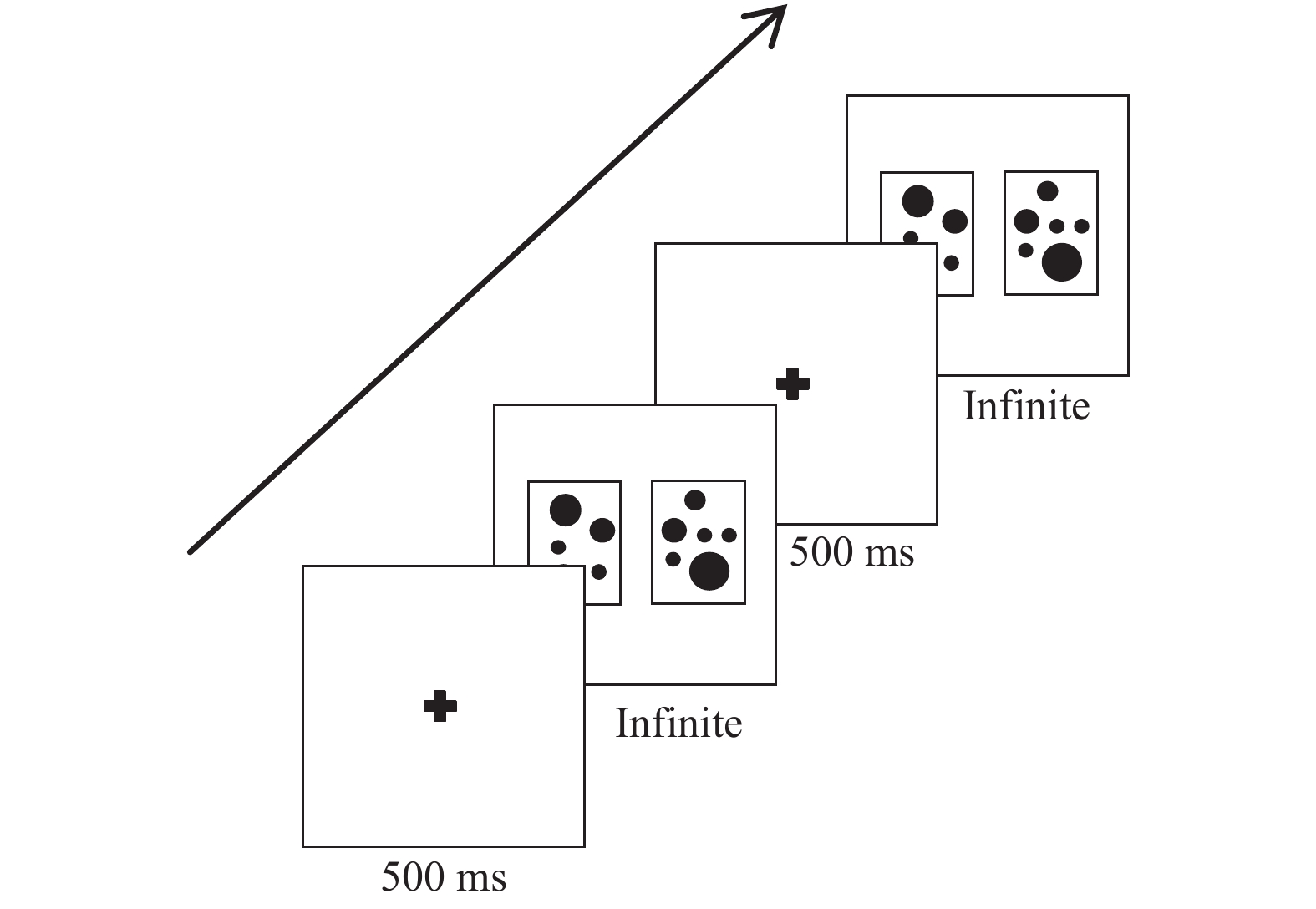 |
| 图 1 非符号比较任务实验流程 |
采用正确率、反应时和韦伯分数作为测量指标,被试的韦伯分数基于心理物理学模型来进行计算评估。该模型认为以数感任务正确率拟合的模型符合高斯正态分布,数感任务中点阵点数n1和n2符合高斯正态分布,其平均表征为高斯随机变量x1和x2,标准差为韦伯分数乘以平均数。点阵中大点数与小点数之差为n2–n1,标准差为
韦氏智力测验积木和词汇分测验(张厚粲, 2009):这些任务分别用来测量被试的空间能力以及言语能力。韦氏智力测验中的积木测验是给被试一定数目的积木,让被试在规定的时间内摆出指定的图形,同时根据被试的不同年龄,开始的题目难度也是不一样的;而词汇测验则是给被试口头呈现一个词汇,被试要做的就是解释该词汇的意思,开始题目的选择根据被试年龄大小来确定。主试根据被试的作答情况来进行记录以及分数的统计。
3 研究结果 3.1 以正确率为测量指标因为数感能力受到智力因素的影响,以下所有数据处理结果都以瑞文标准推理测验得分以及韦氏智力测验中积木和词汇分测验得分的总智力作为协变量进行分析。本研究我们先对303名被试的正确率进行4(被试分组)×6(点数比例)重复测量方差分析,各被试类型描述性统计结果见表1。
| 表 1 不同点数比例下非符号任务正确率的描述性统计量(M±SD) |
结果显示,被试类型主效应显著,F(3, 298)=7.15,p<0.001,η2=0.067。LSD事后比较分析发现正常组儿童的正确率(0.83±0.01)显著大于计算障碍组(0.78±0.01)、阅读障碍组(0.78±0.01)以及双障碍组(0.76±0.01)儿童的正确率,而在三组障碍儿童被试之间两两均没有显著差异。这说明计算障碍、阅读障碍以及双障碍儿童和正常儿童的确存在数感缺陷。点数比例主效应显著,F(5, 1490)=8.60,p<0.001,η2=0.028。LSD事后比较分析发现,除了比例5:6,6:7,7:8两两之间差异不显著外,其他任意两个比例之间差异均达到显著水平,大比例点数正确率(1:2正确率为0.93±0.01;2:3正确率为0.86±0.01;3:4正确率为0.79±0.01)要显著大于小比例点数(5:6正确率为0.70±0.01;6:7正确率为0.72±0.01;7:8正确率为0.71±0.01)的正确率。点数比例与被试类型的交互作用不显著,F(15, 1490)=0.63,p=0.848,η2=0.006。
3.2 以反应时为测量指标结果显示被试类型主效应不显著,F(3, 298)=1.97,p=0.118,η2=0.019,说明在反应时上正常组(1114±31)ms儿童与计算障碍(1152±33)ms、阅读障碍(1086±32)ms、双障碍组(1017±36)ms儿童无显著差异。点数比例主效应不显著,F(5, 1490)=1.35,p=0.241,η2=0.005。点数比例与被试类型的交互作用不显著,F(15, 1490)=1.38,p=0.148,η2=0.014。见表2。
| 表 2 不同点数比例下非符号任务反应时的描述性统计量(M±SD) |
3.3 以韦伯分数为测量指标
首先,我们计算了每个被试的韦伯分数,并且删除不能拟合模型的被试以及韦伯分数超出3个标准差的被试,最终保留计算障碍组61人,阅读障碍组72人,双障碍组50人,正常组74人。其次,以智力为协变量,采用协方差分析,检验了计算障碍组、阅读障碍、双障碍和正常组儿童之间在非符号数量比较任务上的差异。结果显示存在显著的组间差异,F(3, 253)=3.92,p=0.009,η2=0.045。对韦伯分数进行事后LSD多重比较,结果显示,计算障碍组(0.24±0.120)、阅读障碍组(0.23±0.111)和双障碍组(0.27±0.128)被试韦伯分数显著大于正常组(0.19±0.075)被试,但计算障碍组、阅读障碍组和双障碍组被试之间的韦伯分数两两并没有显著差异。这说明计算障碍被试、阅读障碍被试和双障碍被试存在数感缺陷,其近似数量系统敏感性较低。见表3。
| 表 3 非符号数量比较任务韦伯分数的差异比较(M±SD) |
4 讨论
本研究采用非符号数量比较任务检验计算障碍儿童是否存在数感缺陷以及探讨其是否特定于计算障碍儿童。研究发现计算障碍儿童和正常组儿童在非符号数量比较任务上存在显著差异。阅读障碍儿童、双障碍组儿童与正常组儿童在非符号数量比较任务上也存在显著差异。这些结果说明计算障碍儿童的确存在数感缺陷,但是数感缺陷并不特定于计算障碍儿童。
计算障碍儿童与正常儿童相比在正确率和韦伯分数上均存在显著差异,说明计算障碍儿童存在数感缺陷,这一结果与以往多数研究结论相一致(Bugden & Ansari, 2016; Mazzocco et al., 2011; Piazza et al., 2010)。支持了近似数量系统假设,即发展性计算障碍儿童的数量估计系统存在缺陷。近似数量系统负责操作和区分近似数量大小(Dehaene, 2007),被认为是精确符号(数词和阿拉伯数字)表征系统的先驱,而精确符号表征系统负责解决基本的算术问题和更高阶的数学问题(Piazza, 2010),因此,近似数量系统缺陷能够导致符号表征不精确和数学技能较差,从而出现计算障碍。以往影像学研究发现近似数量系统加工与脑内顶内沟区域有关,顶内沟是负责数量表征和数量加工的关键脑区(Ansari & Dhital, 2006; Cantlon et al., 2009; Holloway & Ansari, 2010; Kaufmann et al., 2008)。而计算障碍儿童在执行非符号数量比较任务时,其右侧顶内沟激活要显著弱于正常儿童,导致计算障碍儿童无法像正常儿童那样调用顶叶数量加工资源对小数量距离做出反应(Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007)。此外,近年来大量针对数感训练的研究发现数感训练能够提高儿童数学能力(Hyde, Khanum, & Spelke, 2014; Wilson, Dehaene, Dubois, & Fayol, 2009)。这些研究均间接支持计算障碍儿童可能存在数感缺陷。
与以往没有发现计算障碍儿童数感缺陷的研究相比(Szücs et al., 2013; Rousselle & Noël, 2007),本研究中计算障碍儿童在难度较高(5:6, 6:7和7:8)和较低的比例(1:2和2:3)上成绩均差于正常儿童。这说明任务难度不同并不是计算障碍儿童数感能力研究结果不一致的原因。那么更可能的原因便是被试的样本选择偏差,比如样本所属区域不同,其变异程度可能不同。本研究选择的是重庆市相对偏僻的一个区县,或许正常儿童和障碍儿童的差异比较大。而Szücs等(2013)的样本变异程度较低,这导致正常儿童和障碍儿童在数感方面差异并不是很大。
阅读障碍儿童和双障碍儿童的数感能力均显著低于正常儿童的数感能力,这一结果说明数感缺陷不是特定于计算障碍儿童的。这样的结果有两种可能的原因。其一,数感能力本身可能是一种初级的、基本的能力。研究发现不同物种非符号数量表征的神经编码存在相似性(Nieder, Freedman, & Miller, 2002; Sawamura, Shima, & Tanji, 2002)。人类和动物的大脑顶叶神经不断进化,最终形成了对非符号数量进行表征的具体的近似数量感知系统。随着数字符号的引入和计数的运用,顶叶系统进行了意义深远的改变,先前表征近似数量的神经机制被部分“回收”用于支持精确数字的表征,所以数感随着环境在不断进化,具有环境的基本属性(Piazza & Izard, 2009)。因而,数量估计是一种初级视觉特征的加工,数感像颜色、方向和大小等物理特征的视觉加工一样,也同样具有前注意加工的特点(Burr & Ross, 2008)。它不受物体的大小、颜色、位置等因素的影响,而是受到诸如连通性或者内外关系等拓扑不变量的影响(He, Zhou, Zhou, He, & Chen, 2015)。同时,数感能力是一种基本能力,也是基于阅读障碍儿童和双障碍儿童也存在数感缺陷推论得出的。其二,数感能力可能受一般认知能力影响非常大,比如视空间能力、抑制控制能力。测量数感能力一般采用非符号任务,而该任务中视觉加工的物理特征和数量大小特征纠缠在一起,儿童难以排除物理特征而只进行数量的加工(Soltész, Szücs, & Szücs, 2010),因而该任务可能需要被试较强的视空间能力。也有研究者提出数感能力测验是基于抑制控制能力(Gilmore et al., 2013)。进一步的研究需要对这两种可能性进行检验。
本研究发现阅读障碍儿童也存在数感缺陷,正如上面我们提及的,数感任务的加工需要视空间能力的参与,而研究发现汉语阅读障碍儿童存在视空间能力缺陷。已有研究发现阅读障碍儿童在语音编码和正字法加工上均存在缺陷,汉字作为一种图形文字,对正字法加工有着更高的要求,加工过程需要视觉空间能力的参与,而研究发现汉语阅读障碍儿童存在视空间能力缺陷。因此,阅读障碍儿童存在数感缺陷也就有据可循。相比较于正常儿童,阅读障碍儿童存在数感缺陷这一结果与Träff等人(2017)的研究结果是不一致的,这可能和选取的样本有关。本研究中阅读障碍儿童的数感能力(Mw=0.234,SDw=0.111)和Träff等人的研究中阅读障碍儿童的数感能力(Mw=0.230,SDw=0.060)并无较大差异,t=–0.1605,p=0.873。然而,本研究中正常儿童的数感能力(Mw=0.190,SDw=0.075)却显著高于Träff等人的研究中正常儿童的数感能力(Mw=0.250,SDw=0.140),t=2.915,p<0.01。除此之外,西方以字母为特征语音文字更多需要语言编码,而汉字作为图形文字,字形复杂,结构密集,在识别汉字过程中更多需要知觉辨认和正字法加工,更需要精细的视觉空间分析能力,这可能也是造成中西方关于阅读障碍儿童是否存在数感缺陷研究结果矛盾的一个原因。与Landerl等(2009)的研究一致,本研究的反应时数据也没有探测到阅读障碍组的数感能力与正常组儿童存在差异。然而,根据以往研究结果(Inglis & Gilmore, 2014),正确率,反应时和韦伯分数三种测量指标中正确率指标最可靠,其次是韦伯分数。因此本研究的结果是可靠的。这也启发我们将来的研究应全面报告不同指标的结果,这样便于积累文献,并能与其他研究比较(Dietrich et al., 2015)。但必须说明的是,在障碍组和正常组之间,反应时指标没有明显差异,也可能和本研究中实验材料的呈现时间没有限制有关,这也是本研究的不足之处,需要在今后的研究中改进。
前文已经提及,尽管中国儿童的数学能力相较于西方儿童普遍较好,但是,中国儿童仍然存在较高的计算障碍发病率。探究计算障碍的影响因素,对于找到有效的干预方法尤其重要。本研究的结果启发我们,既然数感缺陷并非特定于计算障碍,那么不管针对计算障碍,阅读障碍还是双障碍儿童,均可以制定相应的数感能力训练课程以改善其状况。
5 结论(1)数感缺陷是计算障碍的一个原因;(2)阅读障碍儿童和双障碍儿童也存在数感缺陷,数感缺陷并非特异于计算障碍。
白学军, 臧传丽. (2006). 发展性计算障碍的类型及成因研究进展. 天津工程师范学院学报, 16(1): 55-58, 73. DOI:10.3969/j.issn.2095-0926.2006.01.016 |
董奇, 林崇德. (2011). 中国儿童青少年心理发育标准化测验简介. 北京: 科学出版社.
|
李红霞, 司继伟, 陈泽建, 张堂正. (2015). 人类的近似数量系统. 心理科学进展, 23(4): 562-570. |
王芳, 路浩, 杨红, 赵晖. (2012). 发展性计算障碍子类型探析. 见 第十五届全国心理学学术会议论文摘要集. 北京: 中国心理学会.
|
张厚粲. (2009). 韦氏儿童智力量表第四版(WISC-Ⅳ)中文版的修订. 心理科学, 32: 1177-1179. |
张厚粲, 王晓平. (1989). 瑞文标准推理测验在我国的修订. 心理学报, 21: 113-121. |
张怀英. (2009). 儿童发展性计算障碍的认知机制研究 (博士学位论文). 华中科技大学, 武汉.
|
张丽, 蒋慧, 赵立. (2018). 发展性计算障碍儿童的数量转换缺陷. 心理科学, 41(2): 337-343. |
张树东, 董奇. (2007). 一~四年级小学生发展性计算障碍的亚类型研究. 心理发展与教育, 23(2): 76-81. DOI:10.3969/j.issn.1001-4918.2007.02.013 |
Ansari, D., & Dhital, B. (2006). Age-related Changes in the Activation of the intraparietal sulcus during nonsymbolic magnitude processing: An event-related functional magnetic resonance imaging study. Journal of Cognitive Neuroscience, 18(11): 1820-1828. DOI:10.1162/jocn.2006.18.11.1820 |
Bartelet, D., Vaessen, A., Blomert, L., & Ansari, D. (2014). What basic number processing measures in kindergarten explain unique variability in first-grade arithmetic proficiency?. Journal of Experimental Child Psychology, 117: 12-28. DOI:10.1016/j.jecp.2013.08.010 |
Barth, H., La Mont, K., Lipton, J., Dehaene, S., Kanwisher, N., & Spelke, E. (2006). Non-symbolic arithmetic in adults and young children. Cognition, 98(3): 199-222. DOI:10.1016/j.cognition.2004.09.011 |
Bugden, S., & Ansari, D. (2016). Probing the nature of deficits in the 'Approximate Number System' in children with persistent Developmental Dyscalculia. Developmental Science, 19(5): 817-833. DOI:10.1111/desc.2016.19.issue-5 |
Burr, D., & Ross, J. (2008). A visual sense of number. Current Biology, 18(6): 425-428. DOI:10.1016/j.cub.2008.02.052 |
Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., & Pelphrey, K. A. (2009). The neural development of an abstract concept of number. Journal of Cognitive Neuroscience, 21(11): 2217-2229. DOI:10.1162/jocn.2008.21159 |
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44(1-2): 1-42. DOI:10.1016/0010-0277(92)90049-N |
Dehaene, S. (2007). Symbols and quantities in parietal cortex: Elements of a mathematical theory of number representation and manipulation. In P. Haggard, Y. Rossetti, & M. Kawato (Eds.), Sensorimotor foundations of higher cognition (pp. 527-574). Oxford: Oxford University Press.
|
Dehaene, S., & Cohen, L. (1997). Cerebral pathways for calculation: Double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex, 33(2): 219-250. DOI:10.1016/S0010-9452(08)70002-9 |
De Smedt, B., & Boets, B. (2010). Phonological processing and arithmetic fact retrieval: Evidence from developmental dyslexia. Neuropsy-chologia, 48: 3973-3981. DOI:10.1016/j.neuropsychologia.2010.10.018 |
De Smedt, B., & Gilmore, C. K. (2011). Defective number module or impaired access? Numerical magnitude processing in first graders with mathematical difficulties. Journal of Experimental Child Psychology, 108(2): 278-292. DOI:10.1016/j.jecp.2010.09.003 |
De Smedt, B., Noël, M. P., Gilmore, C., & Ansari, D. (2013). How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children's mathematical skills? A review of evidence from brain and behavior. Trends in Neuroscience & Education, 2(2): 48-55. |
Dietrich, J. F., Huber, S., & Nuerk, H. C. (2015). Methodological aspects to be considered when measuring the approximate number system (ANS)-a research review. Frontiers in Psychology, 6: 295. |
Di Filippo, G., & Zoccolotti, P. (2018). Analyzing global components in developmental dyscalculia and dyslexia. Frontiers in Psychology, 9: 171. DOI:10.3389/fpsyg.2018.00171 |
Geary, D. C. (2013). Early foundations for mathematics learning and their relations to learning disabilities. Current Directions in Psychological Science, 22(1): 23-27. DOI:10.1177/0963721412469398 |
Gilmore, C., Attridge, N., Clayton, S., Cragg, L., Johnson, S., Marlow, N., … Inglis, M. (2013). Individual differences in inhibitory control, not non-verbal number acuity, Correlate with Mathematics Achievement. PLoS One, 8(6): e67374. DOI:10.1371/journal.pone.0067374 |
Halberda, J., Mazzocco, M. M. M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455(7213): 665-668. DOI:10.1038/nature07246 |
He, L. X., Zhou, K., Zhou, T. G., He, S., & Chen, L. (2015). Topology-defined units in numerosity perception. Proceedings of the National Academy of Sciences of the United States of America, 112(41): E5647-E5655. DOI:10.1073/pnas.1512408112 |
Holloway, I., & Ansari, D. (2010). Developmental specialization in the right intraparietal sulcus for the abstract representation of numerical magnitude. Journal of Cognitive Neuroscience, 22(11): 2627-2637. DOI:10.1162/jocn.2009.21399 |
Hyde, D. C., Khanum, S., & Spelke, E. S. (2014). Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. Cognition, 131(1): 92-107. DOI:10.1016/j.cognition.2013.12.007 |
Inglis, M., & Gilmore, C. (2014). Indexing the approximate number system. Acta Psychologica, 145: 147-155. DOI:10.1016/j.actpsy.2013.11.009 |
Jordan, J. A., Wylie, J., & Mulhern, G. (2010). Phonological awareness and mathematical difficulty: A longitudinal perspective. British Journal of Developmental Psychology, 28(1): 89-107. DOI:10.1348/026151010X485197 |
Kaufmann, L., Vogel, S. E., Wood, G., Kremser, C., Schocke, M., Zimmerhackl, L. B., & Koten, J. W. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex, 44(4): 376-385. DOI:10.1016/j.cortex.2007.08.003 |
Kibbe, M. M., & Feigenson, L. (2015). Young children ‘solve for x’ using the Approximate Number System. Developmental Science, 18(1): 38-49. DOI:10.1111/desc.2014.18.issue-1 |
Landerl, K., Fussenegger, B., Moll, K., & Willburger, E. (2009). Dyslexia and dyscalculia: Two learning disorders with different cognitive profiles. Journal of Experimental Child Psychology, 103(3): 309-324. DOI:10.1016/j.jecp.2009.03.006 |
Mammarella, I. C., Hill, F., Devine, A., Caviola, S., & Szűcs, D. (2015). Math anxiety and developmental dyscalculia: A study on working memory processes. Journal of Clinical & Experimental Neurop-sychology, 37(8): 878-887. |
Mazzocco, M. M., Feigenson, L., & Halberda, J. (2011). Impaired acuity of the approximate number system underlies mathematical learning disability (Dyscalculia). Child Development, 82(4): 1224-1237. DOI:10.1111/cdev.2011.82.issue-4 |
Nieder, A., Freedman, D. J., & Miller, E. K. (2002). Representation of the quantity of visual items in the primate prefrontal cortex. Science, 297(5587): 1708-1711. DOI:10.1126/science.1072493 |
Peters, L., Bulthé, J., Daniels, N., Op de Beeck, H., & De Smedt, B. (2018). Dyscalculia and dyslexia: Different behavioral, yet similar brain activity profiles during arithmetic. NeuroImage: Clinical, 18: 663-674. DOI:10.1016/j.nicl.2018.03.003 |
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends in Cognitive Sciences, 14(12): 542-551. DOI:10.1016/j.tics.2010.09.008 |
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., … Zorzi, M. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition, 116(1): 33-41. DOI:10.1016/j.cognition.2010.03.012 |
Piazza, M., & Izard, V. (2009). How humans count: Numerosity and the parietal cortex. The Neuroscientist, 15(3): 261-273. DOI:10.1177/1073858409333073 |
Price, G. R., Holloway, I., Räsänen, P., Vesterinen, M., & Ansari, D. (2007). Impaired parietal magnitude processing in developmental dyscalculia. Current Biology, 17(24): R1042-R1043. DOI:10.1016/j.cub.2007.10.013 |
Rousselle, L., & Noël, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition, 102(3): 361-395. DOI:10.1016/j.cognition.2006.01.005 |
Rubinsten, O., & Henik, A. (2006). Double dissociation of functions in developmental dyslexia and dyscalculia. Journal of Educational Psychology, 98(4): 854-867. DOI:10.1037/0022-0663.98.4.854 |
Sawamura, H., Shima, K., & Tanji, J. (2002). Numerical representation for action in the parietal cortex of the monkey. Nature, 415(6874): 918-922. DOI:10.1038/415918a |
Schwenk, C., Sasanguie, D., Kuhn, J. T., Kempe, S., Doebler, P., & Holling, H. (2017). (Non-)symbolic magnitude processing in children with mathematical difficulties: A meta-analysis. Research in Developmental Disabilities, 64: 152-167. DOI:10.1016/j.ridd.2017.03.003 |
Shalev, R. S. (2004). Developmental dyscalculia. Journal of Child Neurology, 19(10): 765-771. DOI:10.1177/08830738040190100601 |
Soltész, F., Szücs, D., & Szücs, L. (2010). Relationships between magnitude representation, counting and memory in 4- to 7- year-old children: A developmental study. Behavioral and Brain Functions, 6: 13. DOI:10.1186/1744-9081-6-13 |
Swanson, H. L., & Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 96(3): 471-491. DOI:10.1037/0022-0663.96.3.471 |
Szücs, D., Devine, A., Soltesz, F., Nobes, A., & Gabriel, F. (2013). Developmental dyscalculia is related to visuo-spatial memory and inhibition impairment. Cortex, 49(10): 2674-2688. DOI:10.1016/j.cortex.2013.06.007 |
Träff, U., Desoete, A., & Passolunghi, M. C. (2017). Symbolic and non-symbolic number processing in children with developmental dyslexia. Learning & Individual Differences, 56: 105-111. |
van der Stam, T. (2014). Common factors in dyslexia and dyscalculia: Is phonological awareness the key? (Unpublished master's thesis). Utrecht University, Utrecht.
|
Willcutt, E. G., Petrill, S. A., Wu, S., Boada, R., DeFries, J. C., Olson, R. K., & Pennington, B. F. (2013). Comorbidity between reading disability and math disability: Concurrent psychopathology, functional impairment, and neuropsychological functioning. Journal of Learning Disabilities, 46(6): 500-516. DOI:10.1177/0022219413477476 |
Wilson, A. J., & Dehaene, S. (2007). Number sense and developmental dyscalculia. In D. Coch, G. Dawson, & K. W. Fischer (Eds.), Human behavior, learning, and the developing brain: Atypical development (pp. 212-238). New York: Guilford Press.
|
Wilson, A. J., Dehaene, S., Dubois, O., & Fayol, M. (2009). Effects of an adaptive game intervention on accessing number sense in low-socioeconomic-status kindergarten children. Mind, Brain, & Education, 3(4): 224-234. |
2. School of Sociology and Psychology, Central University of Finance and Economics, Beijing 100081
 2019, Vol. 17
2019, Vol. 17


