| 心算形式对不同近似数量系统敏锐度儿童心算表现的影响 |
2. 山东师范大学心理学院,济南 250358
心算(mental arithmetic)是指不借助外界工具的条件下,依靠思维和记忆直接得出答案的计算方式,也是我们通常意义上讲的“口算”,是日常活动中一种重要的思维活动(张奇, 林崇德, 赵冬梅, 王秀丽, 2002)。心算作为数学运算的一种基本形式,是小学数学教学的重要任务。《九年义务教育全日制小学数学教学大纲》中指出“培养学生的计算能力,要重视基本的口算训练。口算既是笔算、估算和简便计算的基础,也是计算能力的重要组成部分”,要求二年级学生能比较熟练地对两位数加、减进行心算。小学二年级是学习加减法心算的关键时期,目前的教学中却存在着计算正确率下降、心算速度变慢、简便运算方法不够灵活的情况(文玲玲, 陈建华, 2013)。近年来发现,多样化的心算形式练习,不仅有助于激发学生的学习兴趣,还能提高儿童的心算能力。然而,目前小学中有关心算练习的方式仍较为单一,有关心算练习的具体改进方法也多体现在教学和情境设计等方面。仅从理论上对心算形式的应用进行探讨,缺乏实证比较。
早在上世纪70年代,认知心理学便开始将心算作为一个研究主题,探究心算的认知加工机制。之后研究者对心算进行了深入系统研究。一般认为心算涉及三个认知加工环节:编码、运算和反应(Campbell, 2004),将外界呈现的信息进行编码,然后通过内部的算术知识提取或算术运算得到答案。在编码阶段,信息能以不同的表现形式(例如视觉或听觉形式)输入信息通道。具体看来,三重代码模型(triple code model)认为根据任务性质的不同,信息表征的方式也会存在差异(Dehaene & Cohen, 1995)。听觉的言语编码通常负责口语方式的信息输入,而视觉编码则负责阿拉伯数字形式的信息输入。编码复杂性模型也支持信息的表征方式不止一种,不同的表征方式可以同时参与到多种认知过程中(Campbell, 1994)。还有研究发现,输入形式的差异不仅对编码阶段产生影响,对心算的提取过程也存在影响(刘昌, 王翠艳, 2008)。不同的心算任务呈现方式可以引发个体不同的信息表征,读算相对于以往教学中常用的视算方式,通过视觉和听觉两种表征方式对题目信息进行输入,可能对题目信息有更充分的加工,从而帮助低年级儿童在简单心算时获得更好的心算表现。本研究拟采用小学心算练习中常用的评价标准,准确率和计算时间,探究小学低学段儿童在不同心算形式下的心算表现。
心算通常指对精确数量的运算,而估算与其涉及到一些共同的心理加工活动;二者联系密切且估算可以增加心算的潜能,帮助心算更好地进行(Rubenstein, 1985; Reys, Bestgen, Trafton, & Zawojewski, 1984)。ANS敏锐度作为数量估算能力的表现,与数学技能显著相关(Halberda, Ly, Wilmer, Naiman, & Germine, 2012; Pinheiro-Changas et al., 2014)。具体来看,人类出生时就伴有一种用非符号行为表示数目的能力(Feigenson, 2011; Izard, Sann, Spelke, & Streri, 2009)。这种称为近似数量系统(approximate number system, ANS; Feigenson, Dehaene, & Spelke, 2004)的非符号性数目表示系统被发现与数学技能相关(Gilmore, McCarthy, & Spelke, 2010; Halberda, Mazzocco, & Feigenson, 2008)。研究表明ANS提供了数字符号与它们所代表的数量之间的联系基础,并支持符号数字知识的进一步发展(Geary, 2013; van Marle, Chu, Li, & Geary, 2014)。当我们涉及到事物的数量而且又不能精确表示时,ANS表征就会被激活并使用。在控制以前的数学技能后,四岁儿童的ANS敏锐度预示了他们六个月后的数学技能(Libertus, Feigenson, & Halberda, 2013)。而对8岁儿童数学能力的类似研究也发现ANS敏锐度可以预测其数学成就(Inglis, Attridge, Batchelor, & Gilmore, 2011)。相比于低ANS敏锐度儿童,高ANS敏锐度的儿童不仅能更好地辨别非符号数字的大小,将近似数量转化为精确数量,而且在早期数学学习中对数字符号也具有更好的理解能力,在数学运算中能更好地抑制干扰,因此,估算可能是简单数字识别和精确计算之间的中间步骤(Pinheiro-Chagas et al., 2014)。总体来看,ANS估算能力在儿童早期数学学习中占有非常重要的地位,而低ANS敏锐度儿童由于符号理解、运算干扰等问题,可能在心算时表现不佳。因此心算形式的探究可能对这个问题有新的启发,相比传统的视算,读算形式能帮助低年级儿童在心算加工时提高注意,并通过视觉和发音两种方式充分输入题目信息,这些可能帮助低ANS敏锐度儿童对数字符号进行更充分的加工理解。本研究中采用点阵比较任务,以其正确率作为个体ANS敏锐度的指标,相比其他的ANS敏锐度测量方法具有更好的可行性以及良好的信度(Chesney, Bjalkebring, & Peters, 2015)。依照正确率进行高、低ANS敏锐度分组,探究不同ANS敏锐度儿童心算表现是否存在差异,以及心算形式对不同ANS敏锐度儿童心算表现可能的影响。
以往研究还发现,心算与工作记忆关系密切。工作记忆指认知活动过程中负责对信息加工和短暂储存的认知系统(Baddeley, 1992)。而心算过程需要在信息加工的同时对另一些相关信息进行短暂储存。Hitch(1978)曾发现,心算过程中发生的错误,常常是因为被试没有能够把运算过程的中间结果正确记录、保存到工作记忆中,即心算过程不仅应记住需要计算的数字,还必须对计算过程中的数字信息加以保持。此外,在进行简单加减法心算时,工作记忆对心算结果的影响程度仍存在争议(Logie, Gilhooly, & Wynn, 1994; 匡华, 2008)。为避免工作记忆影响儿童ANS敏锐度与心算表现之间的关系,本研究拟将工作记忆作为协变量控制。本研究针对小学数学教学中亟待寻找有效的、新颖的心算形式的现状,对不同心算形式的实际效果进行实验对比,为小学二年级心算教学方式的创新提供支持;并进一步从不同的心算形式的条件下,探究高、低ANS敏锐度(即ANS敏锐组、ANS迟钝组)儿童心算表现的差异。研究预期:在控制协变量的条件下,(1)不同心算形式显著影响儿童心算的正确率和反应时,读算形式能帮助儿童取得更好的心算成绩;(2)心算形式对不同ANS敏锐度儿童心算表现的影响存在差异,心算形式与ANS敏锐度分组间有显著的交互作用。
2 方法 2.1 被试从山东省济宁市某普通小学选取二年级学生129人,剔除未完成点阵比较任务的被试17人,最后获得有效被试112人。按照前后27%的原则从点阵比较任务得分中筛选出低分组30人(男18人,平均年龄8.06±0.24岁;女12人,平均年龄8.08±0.52岁)和高分组30人(男14人,平均年龄8±0.56岁;女16人,平均年龄8.13±0.55岁),分别作为ANS迟钝组和ANS敏锐组。实验结束后,每个被试给予小礼品。
2.2 实验设计采用2(ANS敏锐度分组:敏锐组、迟钝组)×2(心算形式:视算、读算)的两因素被试间设计。自变量为ANS敏锐度分组、心算形式,因变量为心算的正确率和反应时。工作记忆得分作为协变量。
2.3 实验工具与材料 2.3.1 点阵比较任务参考Halberda等(2008)的研究,采取点阵比较任务测量儿童的ANS敏锐度。通过电脑屏幕呈现出两个数目不同的黄色点阵,要求被试比较左右两边点阵哪边点数多。首先,在屏幕上呈现1000 ms注视点,之后出现点数图片,图片呈现1000 ms后消失,由被试进行按键选择,左边点数多按“S”键,右边点数多按“L”键(牛玉柏, 时冉冉, 曹贤才, 2016)。点的数量比率为1:2、2:3、3:4、4:5、5:6、6:7、7:8、8:9、9:10,每种比率点有两种具体的数字组合,每种比例的一半试次左边点多,一半试次右边点多,两边点的总表面积相等。共5个练习试次,72个实验试次。将被试完成任务的正确率作为其点阵比较任务的得分。
2.3.2 自动化工作记忆测验自动化工作记忆测验(automated working memory assessment, AWMA)由英国学者Alloway(2007)编制,用于评估4-22岁个体的工作记忆能力。自动化工作记忆测验共12个分测验,根据国内已有研究(吕娜, 2015; 李红霞, 2016)和本研究的目的,选取3个分测验:数字回忆测验(digit recall)、点阵图片测验(dot matri)和反向数字回忆测验(backward digit recall)分别评估儿童的语音环路、视空模板和中央执行成分。AWMA软件会将各项分测验中的原始得分转化标准化后的分数。本实验中将三个分测验标准化后分数的总分作为工作记忆得分。三个测验的信度系数分别为0.84, 0.83, 0.64。
数字回忆测验:主试匀速读出数字,读完每串数字后由被试口头回答听到的数字,每组有4个试次,当4个试次全对时进入下一组,出现错误时增加1个试次,最多6个试次,错误3次,该分测验终止。共9组数字,分别从1位数逐渐增加到9位数。每个试次的数字随机组成,一串数字中没有重复的数字。被试需听完主试读出的完整一串数字再进行反应,不能出现复述或跟读。正式实验前呈现1~3个数字的练习试次各一次。
点阵图片测验:在4×4的栅格上呈现红色圆点,每幅图片上红点的位置不同,每张图片呈现2 s,需要被试记住每张图上红点所在的位置,图片呈现完成后,要求被试在空白的4×4栅格上依次指出红点的位置。实验从一次呈现1张图片开始,逐渐增多每组连续呈现的图片数量,最多每组连续呈现7张图片。每组有4个试次,当4个试次全对时进入下一组,出现错误时增加1个试次,最多6个试次,错误三次该分测验终止。在实验过程中,被试需要看完连续呈现的图片再进行反应。正式实验前连续呈现1~2张图片的练习试次各一次。
反向数字回忆测验:主试匀速读出一串数字,被试在不出声复述前提下,将这串数字反向回忆出来,如主试读“3 8”,被试回答“8 3”。每组有4个试次,当4个试次全对时进入下一组,出现错误时增加1个试次,最多6个试次,错误三次该分测验终止。共6组数字,分别从2个数字逐渐增加到7个数字。每个试次由数字随机组成,一串数字中没有重复的数字。被试需听完主试读出的完整一串数字再进行反应,过程中不能出现复述或跟读。正式实验前连续呈现2~3个数字的练习试次各一次。
2.3.3 心算测验心算测验根据人教版小学二年级数学教材编制18道两位数以内的加法题目,题目分为6个难度:整十数加法、整十数和非整十数加法、不进位的非整十数加法、个位数与非整十数的进位加法、个位数进位的加法、个位与十位都进位的加法(匡华, 2008)。测验题目由两名二年级数学老师根据二年级数学心算要求协助编制完成。题目中较小的数在加号左侧,较大的数在加号右侧。
2.4 实验程序实验时间是在3月下旬到4月初,两位数心算教学已全部完成。实验程序共分为3个阶段。阶段1,筛选被试,在学校计算机教室对被试进行集体施测,采用E-prime程序呈现点阵比较任务,每批被试由4名主试指导进行实验。依照点阵比较任务正确率进行高低排序,将排序的前、后27%的被试分为高、低ANS敏锐度组;阶段2,工作记忆测量,采取个体施测,对筛选出的被试进行AWMA工作记忆测验;阶段3,心算测验,将筛选出的高、低ANS敏锐度组被试,分别随机分配到对应的两种心算形式组中,每组30人。采取个体施测,通过E-prime程序对被试呈现不同形式的心算测验,由计算机程序随机排列呈现题目的序列,正式试验前呈现2道整十数加法题作为练习。
视算任务:采用电脑对被试进行单独施测,屏幕上每次先出现一个注视点,持续1500 ms后呈现一道加法题,题目呈现时间不限制(匡华, 2008)。要求被试在不出声的前提下心算得出答案向主试口头汇报,同时按下“J”键,按键后呈现下一试次。由电脑记录呈现题目到按下“J”键的反应时间。
读算任务:屏幕上每次先出现一个注视点,持续1500 ms后呈现一道加法题,要求被试在看题的同时出声读题并心算得出答案,得出答案时向主试口头汇报,同时按下键盘“J”键,按键后呈现下一试次。由电脑记录呈现题目到按下“J”键的反应时间。
3 结果 3.1 儿童ANS敏锐度高低分组的有效性以被试在点阵比较任务中得出的正确率作为其近似数量系统敏锐度的指标,根据正确率的高低进行排序,得出前27%和后27%的被试作为ANS敏锐组(n=30)和ANS迟钝组(n=30)。对高低分组的ANS敏锐度进行独立样本t检验,t(58)=–20.70,p<0.001,高低分组的ANS敏锐度存在显著差异(M敏锐组=0.90, SD=0.03;M迟钝组=0.65, SD=0.06),分组有效。
3.2 心算形式、ANS敏锐度对儿童心算表现的影响被试在两种心算形式下的心算正确率和心算反应时及工作记忆得分的描述统计结果见表1。以工作记忆总分作为协变量,心算形式和ANS敏锐度分组为自变量,心算正确率和反应时分别为因变量,进行协方差分析。
以心算正确率为因变量,工作记忆为协变量,经回归系统同构型检验ANS敏锐度分组、心算形式与工作记忆交互作用不显著,可以进行协方差分析,F(4, 57)=0.56,p>0.05。协方差分析结果发现敏锐度分组的主效应显著,F(1, 57)=16.23,p<0.001,η2=0.23,敏锐组正确率(0.98)显著大于迟钝组(0.91);心算形式的主效应显著,F(1, 57)=18.67,p<0.001,η2=0.25,读算正确率(0.98)显著大于视算(0.92)。协变量工作记忆的主效应不显著,F(1, 57)=3.64,p>0.05。敏锐度分组与心算形式的交互作用显著,F(1, 55)=8.43,p<0.01,η2=0.13。简单效应分析发现在视算形式下,不同分组的心算正确率差异显著,F(1, 27)=19.11,p<0.001,η2=0.41;在读算形式下,不同敏锐度分组间的心算正确率差异不显著,F(1, 27)=0.882,p>0.05。读算可以帮助ANS迟钝组的儿童取得更好的心算正确率。
| 表 1 不同心算形式下被试的心算正确率和反应时间(M±SD) |
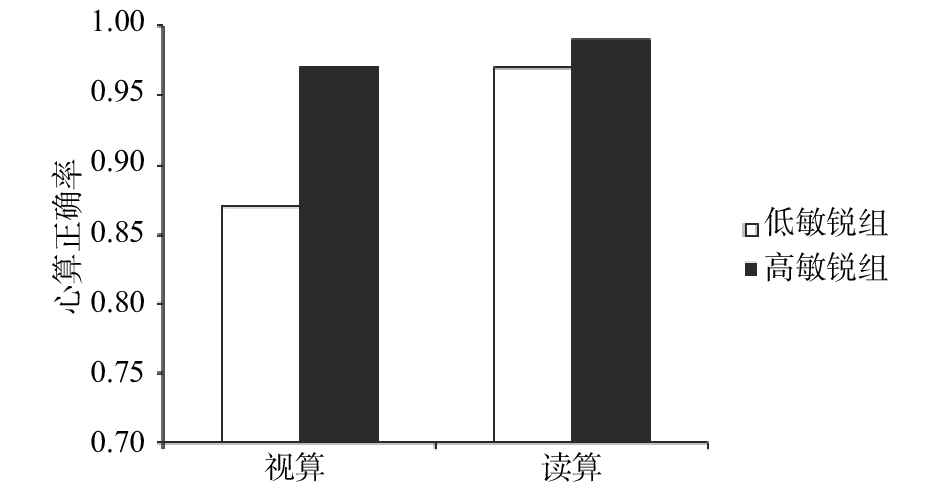 |
| 图 1 心算形式与敏锐度分组对心算正确率的交互作用 |
以心算反应时为因变量,工作记忆为协变量,经回归系统同构型检验ANS敏锐度分组、心算形式与工作记忆交互作用不显著,F(4, 55)=0.41,p>0.05。结果表明,敏锐度分组的主效应不显著,F(1, 57)=0.09,p>0.05;心算形式的主效应不显著,F(1, 57)=0.08,p>0.05。协变量主效应不显著,F(1, 57)=1.21,p>0.05。此外,敏锐度分组与心算形式的交互作用不显著,F(1, 55)=0.45,p>0.05。
由上述结果可知,心算形式与敏锐度分组对心算正确率的交互作用显著,在读算形式下,迟钝组被试的正确率与敏锐组无显著差异,结合主效应的分析,可能说明在小学早期心算教学中,读算形式不仅可以帮助学生取得更好的心算表现,还能使低ANS敏锐度的儿童获得更高的心算正确率。
4 讨论 4.1 不同心算形式对心算表现的影响本研究将被试随机分配成等人数的两组,分别采用视、读算的形式完成一套相同的心算题目。考虑到工作记忆的差异可能会对儿童心算成绩产生影响,测得工作记忆总分作为协变量。结果显示,在控制工作记忆得分的条件下,不同心算形式对心算正确率的影响显著。心算形式的主效应分析发现读算形式下心算正确率显著高于视算,这存在两种可能解释:首先,从工作记忆的角度,尽管视算形式下儿童可以很好地利用其工作记忆中的视空模板成分,在心算过程中可以较好保持题目信息与运算过程,但读算过程相比普通的视算,儿童需要出声读题,能更好地利用语音环路保存题目信息,并且在读题时,为了准确读出题目,可能也使他们付出比视算更多的注意。其次,编码复杂性模型可以从另一个角度进行解释。根据编码复杂性模型,不同通道的表征可以参与到多种认知过程中,而读算形式下心算题目通过视觉信息和听觉信息两种表征方式输入,这些输入的不同表征会影响后续的心算加工(Campbell, 2004)。尽管不同心算形式对于心算过程中具体成分的影响还需进一步考察,但从正确率来看,读算相比于普通的视算,可以帮助低年级小学儿童提高简单加法心算的正确率。
4.2 心算形式、ANS敏锐度分组对心算表现的影响本研究将点阵比较任务的正确率作为ANS敏锐度的指标,通过排序进行高低分组,在常规的视算形式下,敏锐组取得了更好的心算成绩。这支持了已有发现,即点阵比较任务中的正确率能显著预测符号数字知识(van Opstal & Verguts, 2011) 且儿童的ANS敏锐度与数学能力呈显著正相关(Inglis et al., 2011)。进一步比较不同心算形式下敏锐度分组的心算表现,发现不同分组的心算表现会受到心算形式的制约。通过对交互作用的简单效应分析,在读算形式下,不同敏锐度分组的心算正确率无显著差异,迟钝组儿童达到了和敏锐组儿童相似的高正确率。一般认为,人类对于数字运算具有两套表征系统,即表征4及4以下数字的精确数量系统和4以上数字的近似数量系统(章雷刚, 2007)。ANS估算能力可能是简单数字识别和精确计算之间的中间步骤,相比高ANS敏锐度,低ANS敏锐度儿童表现出数字符号的理解能力较差,不能较好抑制数学运算中的干扰(Pinheiro-Chagas et al., 2014)。通过研究我们发现,传统的视算形式下迟钝组的心算正确率确实显著低于敏锐组,然而使用读算后迟钝组的心算正确率显著提升,这可能由于相比传统的视算,读算形式能帮助低年级儿童在心算加工时提高注意,并通过视觉和发音两种方式充分输入题目信息,这些可能帮助低ANS敏锐度儿童对数字符号进行更充分的加工理解。相比视算,儿童在读算时需要出声读题,加强了被试的注意水平。这种前期对于题目信息的充分输入和加工,可能在一定程度上帮助低ANS敏锐度儿童更好地辨别近似数量的大小并进行更精确的加工,更高的注意水平可能也降低了无关信息的干扰,从而更好地进行数字运算。可以认为,读算形式不仅可以帮助低年级小学儿童提高两位数加法的心算表现,获得更高的正确率,还帮助低ANS敏锐度儿童取得和高ANS敏锐度儿童相似的高心算成绩。
4.3 实际意义与未来展望在小学低学段数学学习中,读算形式可以对儿童的心算学习起到多方面的帮助作用。首先,小学阶段的儿童常表现出喜欢思考、思维活跃等特点,但由于年龄较小,解决综合性问题的能力较为不足,不能独立理解和完成综合性的数学问题,而心算练习有助于儿童数学兴趣的培养和数学能力的提升。相比于其他的心算形式,读算可以更好地提高儿童在早期心算练习时的正确率,增强儿童数学学习的自信心和兴趣。其次,本研究的结果有助于帮助数学困难儿童,大量研究表明,数学困难儿童的ANS 敏锐度显著低于正常发展的同龄儿童(李红霞, 司继伟, 陈泽建, 张堂正, 2015)。基于当前教育研究中发现心算形式对儿童心算表现可能存在影响而又缺少实验支持的背景,结合已有的数学成绩与ANS敏锐度、工作记忆与心算表现的研究,本研究以工作记忆为协变量,探究心算形式对不同ANS敏锐度可能存在的影响。实验设计模仿现实教学中不同心算形式的测验过程,具有很高的生态效度。对于ANS敏锐度较低的儿童,读算可能帮助他们弥补ANS敏锐度上的缺陷,缩小与高敏锐度儿童间的心算表现差异。在儿童数学学习中,心算学习将很大程度影响中、高年级计算能力的形成。因此,本研究具有较高的实际意义,为现实教学中常用的心算形式提供了实证证据,证明读算能帮助儿童取得更好的心算表现,并验证了不同ANS敏锐度儿童简单心算表现的差异,且读算可能帮助低ANS敏锐度儿童取得与高ANS敏锐度儿童相似的成绩,避免低ANS敏锐度的儿童在数学学习初期就过早“掉队”,为其后面的数学学习打下良好基础。
需要指出的是,本研究也存在一定的局限性。本研究中探究小学二年级儿童的简单加法心算,将工作记忆作为协变量,而已有研究表明,在复杂心算中工作记忆可能起到更大作用(Logie et al., 1994)。因此可在复杂心算问题中,对工作记忆与心算表现及ANS敏锐度的关系做进一步探究。此外,有关ANS敏锐度的测量任务,正如曹贤才,时冉冉和牛玉柏(2016)发现,当前研究中ANS 敏锐度测量任务存在着信效度不足的问题。为使ANS敏锐度的高低分组所得出的结论更具代表性,应对ANS敏锐度测量任务进一步标准化,对于不同年龄的被试确定固定的数量比率和呈现时间。
5 结论本研究得出以下结论:
(1)在控制工作记忆后,心算形式与ANS敏锐分组都显著影响小学低年级儿童心算的正确率,读算形式下儿童的心算表现最好,而高ANS敏锐度儿童取得更高的心算正确率;
(2)采用读算形式时,低ANS敏锐度儿童可以提高心算正确率且达到与高ANS敏锐度儿童相似的表现。读算可能是提高小学儿童简单心算表现的有效形式,并且能提高低ANS敏锐度儿童的正确率。
曹贤才, 时冉冉, 牛玉柏. (2016). 近似数量系统敏锐度与数学能力的关系. 心理科学, 39(3): 580-586. |
匡华. (2008). 工作记忆与儿童加减法心算(硕士学位论文). 华中师范大学, 武汉.
|
李红霞. (2016). 工作记忆成分、近似数量系统精确性对个体算术策略运用的影响: 来自行为与ERP的证据(硕士学位论文). 山东师范大学.
|
李红霞, 司继伟, 陈泽建, 张堂正. (2015). 人类的近似数量系统. 心理科学进展, 23(4): 562-570. |
刘昌, 王翠艳. (2008). 心算的加工机制: 来自认知神经科学的研究. 心理科学进展, 16(3): 446-452. |
吕娜. (2015). 工作记忆中央执行在算术估计策略运用中的作用: 行为与ERP证据(硕士学位论文). 山东师范大学.
|
牛玉柏, 时冉冉, 曹贤才. (2016). 学前儿童近似数量系统敏锐度与符号数学能力的关系. 心理发展与教育, 32(2): 129-138. |
文玲玲, 陈建华. (2013). 关于小学低年级有效开展听算训练的若干思考. 现代基础教育研究, 10(2): 127-130. |
章雷刚. (2007). 大, 小数量表征的心理机制(硕士学位论文). 浙江大学.
|
张奇, 林崇德, 赵冬梅, 王秀丽. (2002). 小学生加法口算速度和广度的发展研究. 心理发展与教育, 18(1): 16-21. |
Alloway, T. P. (2007). Automated working memory assessment. London: Pearson Assessment.
|
Baddeley, A. (1992). Working memory. Science, 255(5044): 556-559. DOI:10.1126/science.1736359 |
Campbell, J. I. D. (1994). Architectures for numerical cognition. Cognition, 53(1): 1-44. DOI:10.1016/0010-0277(94)90075-2 |
Campbell, J. I. D. (2004). Handbook of mathematical cognition. New York: Psychology Press.
|
Chesney, D., Bjalkebring, P., & Peters, E. (2015). How to estimate how well people estimate: Evaluating measures of individual differences in the approximate number system. Attention, Perception, & Psychophysics, 77(8): 2781-2802. |
Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1(1): 83-120. |
Feigenson, L. (2011). Predicting sights from sounds: 6-month old infants’ intermodal numerical abilities. Journal of Experimental Child Psychology, 110(3): 347-361. DOI:10.1016/j.jecp.2011.04.004 |
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8(7): 307-314. DOI:10.1016/j.tics.2004.05.002 |
Geary, D. C. (2013). Early foundations for mathematics learning and their relations to learning disabilities. Current Directions in Psychological Science, 22(1): 23-27. DOI:10.1177/0963721412469398 |
Gilmore, C. K., McCarthy, S. E., & Spelke, E. S. (2010). Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition, 115(3): 394-406. DOI:10.1016/j.cognition.2010.02.002 |
Hitch, G. J. (1978). The role of short-term working memory in mental arithmetic. Cognitive Psychology, 10(3): 302-323. DOI:10.1016/0010-0285(78)90002-6 |
Halberda, J., Ly, R., Wilmer, J. B., Naiman, D. Q., & Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences of the United States of America, 109(28): 11116-11120. DOI:10.1073/pnas.1200196109 |
Halberda, J., Mazzocco, M. M. M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455(7213): 665-668. DOI:10.1038/nature07246 |
Inglis, M., Attridge, N., Batchelor, S., & Gilmore, C. (2011). Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review, 18(6): 1222-1229. |
Izard, V., Sann, C., Spelke, E. S., & Streri, A. (2009). Newborn infants perceive abstract numbers. Proceedings of the National Academy of Sciences of the United States of America, 106(25): 10382-10385. DOI:10.1073/pnas.0812142106 |
Libertus, M. E., Feigenson, L., & Halberda, J. (2013). Is approximate number precision a stable predictor of math ability? Learning and Individual Differences, 25, 126–133.
|
Logie, R. H., Gilhooly, K. J., & Wynn, V. (1994). Counting on working memory in arithmetic problem solving. Memory & Cognition, 22(4): 395-410. |
Pinheiro-Chagas, P., Wood, G., Knops, A., Krinzinger, H., Lonnemann, J., Starling-Aalves, I., … Haase, V. G. (2014). In how many ways is the approximate number system associated with exact calculation?. PLoS One, 9(11): e111155. DOI:10.1371/journal.pone.0111155 |
Rubenstein, R. N. (1985). Computational estimation and related mathematical skills. Journal for Research in Mathematics Education, 16(2): 106-119. DOI:10.2307/748368 |
Reys, R. E., Bestgen, B. J., Trafton, P. R., & Zawojewski, J. S. (1984). Computational estimation instructional materials for the middle grades. Final report. Washington, DC: National Science Foundation.
|
van Marle, K., Chu, F. W., Li, Y., & Geary, D. C. (2014). Acuity of the approximate number system and preschoolers’ quantitative development. Developmental Science, 17(4): 492-505. DOI:10.1111/desc.2014.17.issue-4 |
van Opstal, F., & Verguts, T. (2011). The origins of the numerical distance effect: The same-different task. Journal of Cognitive Psychology, 23(1): 112-120. DOI:10.1080/20445911.2011.466796 |
2. School of Psychology, Shandong Normal University, Jinan 250358, China
 2018, Vol. 16
2018, Vol. 16


