| 不同亚型数学学习困难儿童应用题问题表征过程的研究 |
数学学习困难(mathematics learning disability, MD)是学习困难的主要类型之一,其发生率为6%~10%(Geary, Hoard, Byrd-Craven, & DeSoto, 2004)。美国精神医学学会精神障碍诊断第5版(DSM-5)将数学学习困难定义为不因教育机会不充分、智力障碍、神经性或感觉障碍、神经认知障碍造成的特定数学学业技能发育受损,存在数字感、算术事实和计算、数学推理等方面的困难;阅读困难(reading disability, RD)是指不因教育机会不充分、智力障碍、神经性或感觉障碍、神经认知障碍造成的特定阅读技能发育受损,伴有费力地读字、难以理解所阅读内容的意思、拼写与书面表达困难(美国精神医学学会, 2015)。
数学学习困难儿童按照是否与其他特定学习障碍共病,一般分为单纯型(只存在数学困难)和混合型(数学与阅读困难在同一个体上共生),其在数学应用题的表现一直受到研究者的高度关注(Fuchs & Fuchs, 2002; Hanich, Jordan, Kaplan, & Dick, 2001; Cirino, Fuchs, Elias, Powell, & Schumacher, 2015)。Fuchs等以普通学生作为参照组,比较小学四年级单纯型和混合型学生的差异,分析了学生在计算应用题、复杂应用题和实际问题上的表现。结果表明,普通学生和其他两组学生在计算应用题、复杂应用题和实际问题上存在显著差异,单纯型和混合型数困儿童在复杂应用题和实际问题上表现上存在差异。大量研究表明,单纯型在数学应用题的表现显著优于混合型数困儿童,但其应用题解决的过程机制差异尚不明晰,需要进一步研究。本研究的主要目的是考察拥有不同解题能力的学生在应用题问题表征过程的差异,特别是单纯型和混合型数困儿童之间的差异。
数学应用题解决是学习者为了适应情境的需要,运用过去所习得的数学知识技能以寻求解答的过程(Kahney,1993)。数学问题解决作为一种高层次的心智活动,从问题的产生到解决,涉及许多复杂的心理过程(Novak & Tassell,2017;Thevenot & Barrouillet,2014;Swanson,2004)。因此从认知心理学视角探讨问题解决的过程模型已成为众多学者关注的研究问题。Mayer(1985)运用信息处理理论与问题空间理论,提出了数学应用题解决的过程模型,包括问题表征、寻找解决方法两个阶段。Mayer认为问题表征由两个步骤组成:问题理解、问题整合。该模型有助于解释儿童在问题表征过程中每个加工阶段的特点,也为本研究探讨不同亚型数学学习困难儿童应用题解决的表征过程奠定理论基础。
问题理解,主要指解题者读懂描述问题的每一个句子,这是将问题中的每一陈述转换成解题者内部的心理表征的过程,并能用自己的语言重复问题的条件。问题理解涉及将问题的语言转换成可理解的形式,以及区分问题中的有效信息与无关信息。理解是一种有效的阅读策略。在阅读的过程中,学生接收到的信息越多,那么其对文本的理解越深刻。在数学学科中,数学问题可能包含与题意毫无关联的信息,而多余条件会干扰学生建立准确的表征模型(邢强,单永明,2013)。因此,在理解题意的过程中,学生能够对信息有所筛选,识别题干中的有关信息与无关信息就显得尤为重要。研究者以四年级数困组学生和普通组学生为被试,发现无论是无关语义信息,还是无关数值信息,数困组学生在数学问题解决的过程中使用的频率显著高于普通组学生(Passolunghi,Marzocchi,& Fiorillo,2005)。Krawec(2014)考察八年级数困组学生和普通组学生受无关信息的影响,同样发现数困组学生使用无关信息的频率高于普通组学生。因此,本研究的第一个目的就是探索不同亚型数困儿童对应用题理解的差异。研究假设一:单纯型与混合型数困儿童在识别有关信息、无关信息上存在差异。
问题整合,指在信息感知理解的基础上,通过形成一个反映问题中各部分关系的结构表征来使问题可视化。有效的解题者通常会将问题整合成视觉表征结构。视觉表征是指内部图像(如,心理图式)和外部图像的建构与形成。Hegarty和Kozhevnikov(1999)将视觉表征分为:图像表征(pictorial representation),是指描述问题中一个或多个客体视觉外观的表征方式;图式表征(schematics representation),是指用来反映问题各成分之间空间关系的表征方式。已有研究发现,高空间视觉化能力者更善于使用视觉空间表征策略解决数学应用题,低空间视觉化能力学习者的表征更随机(俞国良, 曾盼盼, 2003)。此外,高空间视觉化能力者善于激活图式表征策略,而低空间视觉化能力者更多建构图像表征策略(van Garderen, 2006)。而最新研究发现, 单纯型数困儿童的空间视觉能力显著高于混合型数困儿童(赖颖慧, 朱小爽, 黄大庆, 陈英和, 2014;Swanson, 2012)。由此提出研究假设二:单纯型数困儿童比混合型数困儿童擅于运用图式表征策略。
已有研究发现,视觉表征与数学问题解决相关,使用图式表征与数学问题解决的成绩呈显著正相关,而使用图像表征与数学问题解决的成绩呈负相关(Hegarty & Kozhevnikov, 1999)。俞国良和曾盼盼(2003)考察数学问题解决与视觉表征策略使用的关系,发现数学问题解决的正确率与图式表征策略的使用有显著正相关,与图像表征策略的使用有显著负相关。该研究结果是数困组儿童与一般儿童作为一个整体,考察数学问题解决表现与视觉表征策略使用的关系,但未区别不同数困儿童群体上数学问题解决与视觉表征策略使用的关系。本研究的第三个目的是探索视觉表征策略对不同亚型数困儿童应用题解决成绩的作用。研究假设三:图示表征策略对数困儿童应用题成绩有正向显著影响。
2 研究方法 2.1 被试上海市某三所普通小学四年级小学生576人全部进入筛选样本,排除智力水平异常、学习动机低下者,最终筛选出被试87人(平均年龄10.21±0.35,男44人,女43人)。其中单纯型数学学习困难(简称单纯型)的学生28名、混合型数学学习困难(简称混合型)的学生29名,一般学业(简称普通型)的学生30名。参考成就-智力差异模型的认定方法进行筛选(Fuchs, Fuchs, & Prentice, 2004),单纯型被试的选取方式及标准为:最近三次正规数学考试成绩标准分处于后25%,且最近三次正规语文考试成绩标准分位于前70%;研究者与任课老师综合评定其数学学习落后,语文成绩正常;没有明显的视听感官障碍、运动缺陷、情感障碍、社会文化适应不良以及其他躯体或精神疾病。混合型被试的选取标准为:最近三次语文和数学正规考试成绩标准分均位于后25%;任课老师评定其数学、语文学习落后,其他条件与单纯型一致。普通型被试,其数学和语文成绩介于20%-60%之间;任课老师评定其数学、语文学习情况稳定。
排除标准:为了排除智力障碍的学生,根据班主任、数学任课教师日常观察推荐,结合瑞文渐进矩阵测试(Raven, 1976),排除智商低于80的学生。同时,根据学习动机诊断测验(周步成, 1991),排除学习动机低于2个标准差的学生。
2.2 研究工具参考个体数学问题解决视觉表象水平的测量工具(Lean & Clements, 1981),根据《义务教育数学课程标准》对数学问题解决能力的要求,编制多步运算应用题来测量学生的问题表征能力。在测验编制过程中,结合小学四年级的数学教学内容、教学进度与教材呈现方式,与具有20多年教龄的数学老师合作编制27道多步运算的应用题预测题。预测题皆利于运用视觉表征解决。抽取两个自然班的学生进行测试,控制难度系数后选取9道作为口语报告的测验材料。
9道题目包含三个相关条件信息和一个提问。为考查题干语义信息对解题的影响,将其中3道题目每题增加了两个无关语义信息,3道题每题增加了两个无关数值信息,还有3道题保持不变。据此,整套测试题根据题干的语义信息分成相关语义信息、无关语义信息、无关数值信息三类,每类各设3道题,样题见表1。如样题2:超市销售散装果酱,需要知道每瓶果酱的重量来估计运费。在天平秤的一边放3瓶果酱和一个100克砝码,另一边放一个200克砝码和一个500克砝码。这时天平达到平衡,那么一瓶果酱重多少克?该题目包含4个相关信息:(1)在天平秤的一边放3瓶果酱和一个100克砝码;(2)另一边放一个200克砝码和一个500克砝码;(3)天平达到平衡;(4)一瓶果酱重多少克。2个无关语义信息:(1)超市销售散装果酱;(2)需要知道每瓶果酱的重量来估计运费。整套测试题的相关信息得分介于0到36之间,无关语义信息和无关数值信息的得分分别介于0到6之间。最后,整套测试题的正确得分范围从0到9。
| 表 1 测试题的类型与样题 |
2.3 研究程序
(1)实施瑞文渐进矩阵测试、学习动机诊断测验,收集最近三次正规数学考试、语文考试成绩;访谈每个班的班主任和数学任课教师,了解学生的基本情况;根据前述筛选标准确定单纯型数困儿童、混合型数困儿童和普通型儿童。
(2)预试。根据预试结果判断测试材料的适用性,通过反复修改题目,以加强题意表达的准确度。
(3)正式实验。采用口语分析技术对被试的认知加工进行分析,用整套测试题对三组被试进行个别施测。9道测试题以卡片形式随机呈现,每道题的解题时间为3分钟,全程用录像机记录。主试呈现测试题卡,先由主试读题,再由学生自行审题,指导语如下:“请先读题,完成后请示意。(1)请你说出题目中用于解题的重要信息;(2)你在解题时,脑海中是否出现题中所述内容的图像?如果有,你能说出/画出你脑海中的图像吗?(3)请解题。”参照已有研究中的编码方法(Krawec, 2014),研究者对口语报告和解题过程进行计分、统计与分析。鉴于研究目的是探索单纯型与混合型数困儿童在问题理解阶段的差异,即理解语义顺序、关系、推论或更深层次的意义,故采用主试读题控制费力读字对阅读困难儿童的干扰。在理解问题阶段,先考察被试使用了哪些语义信息,被试口头报告表明使用了的信息上计1分,没有证据表明使用该信息计0分;再考察被试在运用视觉表征来解题过程中运用了哪些信息,被试解题过程表明使用了的信息上计1分,没有证据表明使用该信息计0分。如样题1,被试口头报告,“在天平秤的一边放3瓶果酱和一个100克砝码,另一边放一个200克砝码和一个500克砝码,是关键信息”,该被试的解答过程如图1所示,那么具体计分如表2所示。
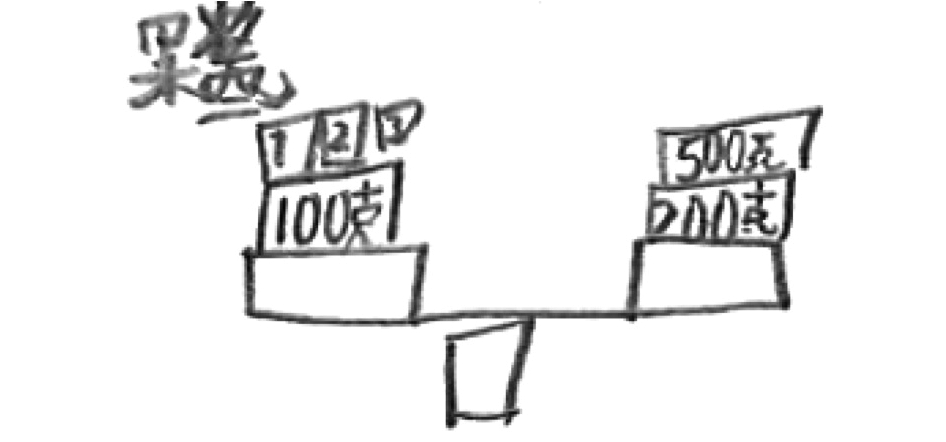 |
| 图 1 被试的图解 |
| 表 2 语义表征与视觉表征举例 |
在整合问题阶段,先考察被试是否使用了视觉表征,有证据表明使用了该策略计1分,若无计0分;再考察使用了视觉表征策略的被试,所采用的策略是归入图像表征或图式表征中的一种。编码过程中,将被试口语报告转录成书面材料,为确保原始数据的准确性采用二次复核的方式。为保证评分的准确性,由研究者与特殊教育专业研究生分别对数据进行评分统计,一致性是91%。对于评分不一致处,双方经讨论达成一致。
3 研究结果 3.1 不同亚型数困儿童问题理解阶段的差异不同亚型数困儿童在数学应用题问题理解过程中,使用各类条件信息的基本情况见表3。方差分析显示:不同亚型数困儿童在语义无关数值信息、视觉相关信息、视觉无关信息上均有显著差异。事后检验发现,在语义无关数值信息上,单纯型、混合型使用的信息数量显著多于普通型,单纯型与混合型不存在显著差异;在视觉相关信息上,普通型所用的信息数量显著多于单纯型和混合型,单纯型与混合型不存在显著差异;在视觉无关信息上,单纯型所用的信息数量显著多于混合型、普通型。
| 表 3 不同亚型数困儿童在应用题问题理解阶段的描述性统计与方差分析 |
3.2 不同亚型数困儿童整合问题阶段的差异
不同亚型儿童在问题整合阶段,使用各类表征方式的基本情况见表4。方差分析显示:不同亚型数困儿童在问题解决的正确率、视觉表征、图像表征、图式表征上均有显著差异。事后检验发现,在问题解题的正确率上,混合型的解题表现显著低于单纯型,单纯型和混合型的解题表现显著低于普通型;在视觉表征上,普通型儿童运用视空表征显著多于混合型儿童,且单纯型与混合型儿童之间无显著差异;在图像表征上,单纯型和混合型使用的程度显著高于普通型,单纯型与混合型不存在显著差异;在图式表征上,单纯型的使用程度显著高于混合型,单纯型和混合型的使用程度显著低于普通型。
| 表 4 不同亚型数困儿童在应用题问题整合阶段的描述性统计与方差分析 |
3.3 不同亚型数困儿童视空表征与数学问题解决成绩的相关性
如表5所示,对于单纯型,数学问题解决的正确率与图像表征呈显著负相关,与图式表征呈显著正相关;对于混合型,数学问题解决的正确率与视觉表征、图式表征都有显著正相关;对于普通型,数学问题解决的正确率与视觉表征、图式表征都有显著正相关,与图像表征呈现显著负相关。
| 表 5 不同类型儿童问题解决得分与表征策略的相关性 |
4 讨论 4.1 单纯型与混合型数困儿童有效识别信息的能力弱,难于利用相关信息和排除干扰信息
不同亚型数困儿童在辨识数学应用题有关信息与无关信息是否存在差异呢?为考察该问题,本研究未采用以往结构良好的问题范式,而是将结构良好问题改编为结构不良问题,增加了无关条件句,而且部分包含无关数值信息。这意味着,被试无法直接利用条件及其所包含的数值信息进行简单代入计算,必须对题设条件进行甄别和筛选。有效的问题解决取决于个体能否准确理解题意,识别相关条件、排除无关条件,然后在识别信息的基础上构建表征,进而解决问题。本研究发现,虽然各组儿童在语义相关条件上不存在差异,但是在视觉有关信息上,单纯型与混合型数困儿童所用的条件数量都显著少于普通儿童,单纯型与混合型数困之间儿童不存在差异。这表明,单纯型与混合型数困儿童有效识别不同类别信息的能力较弱。问题理解阶段所需的知识包括(Mayer, 1992):语言知识,即语言有关的知识(如认识理解问题中的每一个字);语义知识,与实际生活上的事实有关的知识(如1米等于100厘米);事实知识,有关问题形态的知识(如知道求三角形面积公式)。而数困儿童对相关信息识别不充分,可能与其缺乏可供利用的语言知识、语义知识、事实知识的储量、理解与应用能力有关。例如,在本研究发现部分数困儿童甚至会认为,题目中的提问句不是解题的关键信息。
本研究发现,在语义无关数值信息上,单纯型与混合型数困儿童所用的信息数量都显著多于普通儿童,单纯型与混合型数困儿童之间不存在显著差异。这表明,测试题目有些是增加了一些多余的数字条件,单纯型与混合型数困儿童在筛选排除额外数字信息时,都存在困难。本研究发现,部分数困儿童认为样题3中的无关数值条件“小亚跑了200米”是关键信息,其解释为“已知的数据都应该是有用”。这与已有发现类似,数困儿童依靠问题的外显信息,随意提取无关信息(Montague, 1992; Krawec, 2014)。在问题理解阶段,普通型儿童发现题目条件句较多,意识到与往常解题不同,需要甄选数值,而不是立即将疑似数据代入运算,有效地避免对认知冲突的不利信息“视而不见”现象发生(Chinn & Brewer, 1993)。因此,在单纯型和混合型数困儿童解题训练中,可适当让他们接触一些不规则的应用题,即用应用题更加完整的文字信息和多余数值信息锻炼学生的概念性理解,建立数学关系并将数学应用到现实问题情境中的能力。
本研究发现,在视觉无关信息上,单纯型数困儿童所用的信息数量显著多于混合型数困儿童和普通儿童。单纯型与混合型数困儿童的差异,这可能与单纯型和混合型数困儿童之间存在某些认知加工机制的差异有关。单纯型数困儿童在同时性加工上的表现显著低于混合型数困儿童(李清, 2009),使得单纯型数困儿童在理解问题时难以把多个条件整合统一考虑,难以理解题意和各条件之间的关系,将更多的注意放在题目中的数值信息或零散的细节信息。再加之无关信息与任务不相关,无法促进单纯型数困学生深入理解问题,同时占用了工作记忆中的资源,成了一个额外的认知负担,从而影响问题的理解(Paas, Renkl, & Sweller, 2003; 和美君, 刘儒德, 徐乐, 贾玲, 2012)。
4.2 单纯型数困儿童比混合型数困儿童更擅于运用图式表征策略一般地,视觉图像分为以图式为主(即,对问题所描述的空间关系进行图像编码)或以图像为主(即,在问题中描述的对象或人物进行图像编码)。本研究在考察不同亚型数困儿童,分别在使用图式表征策略与图像表征策略的差异。在使用图像表征策略的程度上,单纯型与混合型数困儿童之间无显著差异,且使用次数都高于普通儿童;而在使用图式表征策略上,单纯型显著多于混合型数困儿童,且使用次数都低于普通儿童。这说明,在数学应用题解决的过程中,虽然单纯型与混合型数困儿童都运用了视觉表征策略,但是使用表征策略的质量存在差异,单纯型数困儿童比混合型数困儿童更多地使用抽象、概括的图式表征策略。Van Garderen(2006)也发现不同学习能力的学生在使用表征策略的质量上存在差异,比较小学六年级学困生、普通生和学优生在应用题解决的表现,分析视觉表征的运用与空间可视化能力的关系。结果发现,与数困生和普通生相比, 数优生在空间可视化测量方面表现得更好;数困生使用图像表征策略显著多于数优生,普通生与学困生、数优生之间无显著差异;数优生使用图式表征策略显著多于数困生和普通生,普通生与学困生之间无显著差异。这一发现支持了Hegarty和Kozhevnikov(1999)研究的发现。总体而言,这些结果表明,低空间可视化能力的学生表现出偏好使用图像,也就是不太复杂的图像类型;具有高空间可视化能力的学生更倾向于使用图式,即蕴含更复杂关系的图像类型。
Geary(2004)指出了在解决复杂应用题时,视觉空间能力(即表示概念性知识形式的能力,以及处理空间形式的数学信息的能力)的重要性。正如Smith(1964)所指出的那样,空间可视化技能可能在解决问题中发挥核心作用,因为从问题中抽取信息的过程在某种程度上可能涉及到模式或结构的重制。视觉空间能力缺陷可能会干扰问题解决能力。例如,研究发现有空间定向缺陷的参与者也表现出生成和应用数字线上的不足(Zorzi, Priftis, & Umiltà, 2002)。赖颖慧等(2014)比较单纯型与混合型数困儿童空间能力的差距,发现单纯型数困儿童的空间视觉能力显著优于混合型数困儿童。由此可以解释,单纯型数困儿童使用图式表征策略的能力显著高于混合型数困儿童的原因。
4.3 图式表征策略能促进数困儿童应用题的解决本研究发现,擅长运用图式表征的单纯型数困儿童,数学应用题的正确率较高;而不擅长运用图式表征的混合型数困儿童,数学应用题的正确率较低。这说明,较好地使用图式表征策略的数困儿童,能较好地解决数学应用题。这表明,数学问题表征过程中的图式表征对儿童数学问题解决的重要性。当儿童在理解表征一个问题时,运用视觉表象是一个强大的形象化策略(Hegarty & Waller, 2005),可以用来分析问题结构,为寻找解决方案奠定基础,简化复杂情况,并把抽象的概念变得更具体、熟悉。之所以图式表征策略的使用与数学问题解决有显著正相关,这可能与儿童空间视觉化能力有关。空间视觉化能力是人脑对空间信息表象进行一系列心理操作,是一种建构高质量、不易衰退的表征能力(van Garderen, 2006)。有研究发现数困儿童空间视觉能力与数学问题解决的正确率显著相关(俞国良, 曾盼盼, 2003; Mix & Cheng, 2011)。此外,数学问题解决需要多种认知过程的参与( Montague, Krawec, Enders, & Dietz 2014),其中包括视觉空间工作记忆。视空工作记忆是对客体和空间信息在接受进一步处理前的临时存储与加工(Baddeley, 2012)。有实验证据表明视空工作记忆与数学问题解决之间具有紧密联系(朱晓斌, 王静丽, 李晓芳, 2011; 邢强, 蔡新华, 刘大革, 2015),视空工作记忆较好的儿童具有更充足的工作记忆容量来储存与加工重要的信息,进而帮助个体理解问题,形成最终的解决方案。研究者通过深入探索不同视空间工作记忆成分与各类数学应用题的相关性,进一步发现主动视空间工作记忆对几何应用题解决具有预测力,被动序列视空间工作记忆对文字应用题具有预测力(朱晓斌等, 2011)。
图式表征策略能促进数困儿童应用题的解决,可能还与表征策略的作用有关。关注题目中一个或多个客体生动细微的视觉形象的图像表征策略,会阻碍数学问题的解决,而聚焦题目中一个或多个客体动态空间关系的图式表征策略,能促进数学问题的解决。在数学课堂教学中,教师可能要求学生“画草图”,但未考虑草图可能误导某些学生过分关注一些具体的、生动的图像细节,而忽略问题中客体之间的空间关系。因此,教师对数困儿童进行干预教学时,必须深入分析个体所需的特殊的认知要求,帮助其逐步地构建与使用图式表征策略。
5 结论本研究的结果如下:(1)单纯型与混合型数困儿童有效识别信息的能力弱,难于利用相关信息和排除干扰信息;(2)单纯型数困儿童比混合型数困儿童更擅于运用图式表征策略;(3)图式表征策略能促进数困儿童应用题的解决。
和美君, 刘儒德, 徐乐, 贾玲. (2012). 数学能力与问句位置对小学生数学结构不良应用题表征的影响. 心理发展与教育, 28(3): 276-282. |
赖颖慧, 朱小爽, 黄大庆, 陈英和. (2014). 3-6年级数学学习困难儿童与正常儿童空间能力的比较. 心理与行为研究, 12(1): 36-44. |
李清. (2009). 基于PASS理论的小学数学学习困难儿童应用题问题表征研究(博士学位论文). 华东师范大学.
|
美国精神医学学会. (2015). 精神障碍诊断与统计手册. 张道龙译. 北京: 北京大学出版社.
|
邢强, 蔡新华, 刘大革. (2015). 外部表征、工作记忆对小学生数学应用题解决的影响. 教育研究与实验, (5): 37-42. |
邢强, 单永明. (2013). 文本表述和结构对小学生数学应用题表征的影响. 心理发展与教育, 29(3): 292-298. |
俞国良, 曾盼盼. (2003). 数学学习不良儿童视觉-空间表征与数学问题解决. 心理学报, 35(5): 643-648. |
周步成. (1991). 学习动机诊断测验. 上海: 华东师范大学出版社.
|
朱晓斌, 王静丽, 李晓芳. (2011). 视空间工作记忆和非言语流体智力在小学生数学问题解题中的作用. 心理科学, 34(4): 845-851. |
Baddeley, A. (2012). Working memory: Theories, models, and controversies. Annual Review of Psychology, 63: 1-29. DOI:10.1146/annurev-psych-120710-100422 |
Chinn, C. A., & Brewer, W. F. (1993). The role of anomalous data in knowledge acquisition. Review of Educational Research, 63(1): 1-49. DOI:10.3102/00346543063001001 |
Cirino, P. T., Fuchs, L. S., Elias, J. T., Powell, S. R., & Schumacher, R. F. (2015). Cognitive and mathematical profiles for different forms of learning difficulties. Journal of Learning Disabilities, 48(2): 156-175. DOI:10.1177/0022219413494239 |
Fuchs, L. S., & Fuchs, D. (2002). Mathematical problem-solving profiles of students with mathematics disabilities with and without comorbid reading disabilities. Journal of Learning Disabilities, 35(6): 563-573. |
Fuchs, L. S., Fuchs, D., & Prentice, K. (2004). Responsiveness to mathematical problem-solving instruction, comparing students at risk of mathematics disability with and without risk of reading disability. Journal of Learning Disabilities, 37(4): 293-306. DOI:10.1177/00222194040370040201 |
Geary, D. C. (2004). Mathematics and learning disabilities. Journal of Learning Disabilities, 37(1): 4-15. DOI:10.1177/00222194040370010201 |
Geary, D. C., Hoard, M. K., Byrd-Craven, J., & DeSoto, M. C. (2004). Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology, 88(2): 121-151. DOI:10.1016/j.jecp.2004.03.002 |
Hanich, L. B., Jordan, N. C., Kaplan, D., & Dick, J. (2001). Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology, 93(3): 615-626. DOI:10.1037/0022-0663.93.3.615 |
Hegarty, M., & Kozhevnikov, M. (1999). Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology, 91(4): 684-689. DOI:10.1037/0022-0663.91.4.684 |
Hegarty, M., & Waller, D. (2005). Individual Differences in Spatial Abilities. In P. Shah & A. Miyake (Eds.), The Cambridge handbook of visuospatial thinking (pp. 121–169). New York, NY: Cambridge University Press.
|
Kahney, D. (1993). Problem solving: Current issues (2nd ed.). Milton Keynes: Open University Press.
|
Krawec, J. L. (2014). Problem representation and mathematical problem solving of students of varying math ability. Journal of Learning Disabilities, 47(2): 103-115. DOI:10.1177/0022219412436976 |
Lean, G., & Clements, M. A. (1981). Spatial ability, visual imagery, and mathematical performance. Educational Studies in Mathematics, 12(1): 267-299. |
Mayer, R. E. (1985). Mathematical ability. In R. J. Sternberg (Ed.), Human abilities: An information processing approach (pp. 127–150). San Francisco, CA: Freeman.
|
Mayer, R. E. (1992). Thinking, problem solving, ccognition. New York: W. H. Freeman and Company Press.
|
Mix, K. S., & Cheng, Y. L. (2012). The relation between space and math: Developmental and educational implications. Advances in Child Development and Behavior, 42: 197-243. DOI:10.1016/B978-0-12-394388-0.00006-X |
Montague, M. (1992). The effects of cognitive and metacognitive strategy instruction on the mathematical problem solving of middle school students with learning disabilities. Journal of Learning Disabilities, 25(4): 230-248. DOI:10.1177/002221949202500404 |
Montague, M., Krawec, J., Enders, C. & Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. Journal of Educational Psychology, 106(2): 469-481. DOI:10.1037/a0035176 |
Novak, E., & Tassell, J. L. (2017). Studying preservice teacher math anxiety and mathematics performance in geometry, word, and non-word problem solving. Learning and Individual Differences, 54: 20-29. DOI:10.1016/j.lindif.2017.01.005 |
Paas, F., Renkl, A., & Sweller, J. (2003). Cognitive load theory and instructional design: Recent developments. Educational Psychologist, 38(1): 1-4. |
Passolunghi, M. C., Marzocchi, G. M., & Fiorillo, F. (2005). Selective effect of inhibition of literal or numerical irrelevant information in children with Attention Deficit Hyperactivity Disorder (ADHD) or Arithmetic Learning Disorder (ALD). Developmental Neuropsychology, 28(3): 731-753. DOI:10.1207/s15326942dn2803_1 |
Raven, J. C. (1976). Standard progressive matrices. Oxford, England: Oxford Psychologists Press.
|
Smith, I. M. (1964). Spatial ability: Its educational and social significance. London: University of London Press.
|
Swanson, H. L. (2004). Working memory and phonological processing as predictors of children's mathematical problem solving at different ages. Memory & Cognition, 32(4): 648-661. |
Swanson, H. L. (2012). Cognitive profile of adolescents with math disabilities: Are the profiles different from those with reading disabilities?. Child Neuropsychology, 18(2): 125-143. DOI:10.1080/09297049.2011.589377 |
Thevenot, C., & Barrouillet, P. (2014). Arithmetic word problem solving and mental representations. In R. C. Kadosh & A. Dowker (Eds.), The oxford handbook of numerical cognition. Oxford: Oxford University Press.
|
van Garderen, D. (2006). Spatial visualization, visual imagery, and mathematical problem solving of students with varying abilities. Journal of Learning Disabilities, 39(6): 496-506. DOI:10.1177/00222194060390060201 |
Zorzi, M., Priftis, K., & Umiltà, C. (2002). Brain damage: Neglect disrupts the mental number line. Nature, 417(6885): 138-139. DOI:10.1038/417138a |
 2018, Vol. 16
2018, Vol. 16


