1 引言
由于直线电机伺服驱动系统省去了从旋转运动到直线运动的中间传动环节,实现了所谓的“零传动”,提高了传动刚度、 传动精度和定位精度,具有更大的加速度,且行程不受限制,因而在数控机床进给传动中得到了广泛应用[1]. 而永磁同步直线电机由于其具有结构紧凑、 推力密度大、 惯性低和响应速度快等优点,在直接驱动技术中更受青睐[2, 3, 4]. 但是高性能永磁同步直线电机直接驱动系统需要机械传感器实时检测电机的速度和位置,而机械传感器的存在增加了系统成本、 使得安装维护不便、 且降低了系统可靠性[5, 6]. 因此,近年来国内外许多学者开展了无传感器控制研究,提出了很多有关检测电机速度和位置的估计方法[7],而滑模观测器法由于对电机参数要求不高和对参数变化不敏感,因此凭借其独特的优越性脱颖而出.
滑模观测器估计法[8],就是利用电机本身的数学模型,利用观测电流和实际电流之间的差值来重构电动机的反电动势,以此来估算转子位置. 滑模变结构控制和控制对象的参数变化与外界扰动无关,滑模变结构控制具有响应速度快和鲁棒性强的特点,但其本质上是不连续的开关控制,因此高频切换以及储能器件的惯性效应会引起系统发生抖振现象,从而影响系统的稳态精度. 这种情况在电动机低速运行时尤其明显,进而引起比较大的转矩脉动. 文[9, 10]提出了用各种函数如饱和函数、 线性函数、 积分函数和死区迟滞函数等替代传统的符号函数的新型滑模观测器,在一定程度上削弱了抖振. 文[11]设计了可变截止频率的低通滤波器,这样会使转子位置角的估算更加精确,但是,控制系统将会变得更加复杂,同时也加大了运算量,以至于控制精度及效率都有所下降. 文[12, 13]独出心裁计算转子转速,它没有采用补偿过后的转子位置直接进行微分,而是设计一个锁相环来更精确地估计转子转速,取得了较好的效果. 文[14]把模糊控制引入滑模控制器,高效地柔化高频切换控制作用,缓解保持较小系统稳态误差与平滑抖振之间的矛盾. 文[15]中模糊输入采用电流误差和反电动势. 综上,本文提出将模糊控制引入滑模观测器中,动态调节边界层及切换函数值,以抑制抖动和满足快速到达滑模面的要求,同时借鉴锁相环原理对转速进行估算.
2 改进滑模观测器的设计以常规的PMLSM为分析对象,其在两相静止坐标α轴、 β轴的数学模型[7]为
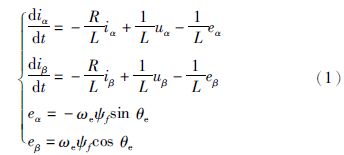
传统的滑模观测器的数学模型[7]:
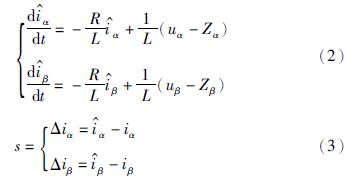
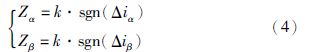
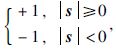 k为滑模系数,Δiα和Δiβ分别为α轴和β轴的电流估计偏差,下面统一简称s. 基于在滑模面中增加边界层平滑抖振的思想,引入饱和函数[16],数学模型变为
k为滑模系数,Δiα和Δiβ分别为α轴和β轴的电流估计偏差,下面统一简称s. 基于在滑模面中增加边界层平滑抖振的思想,引入饱和函数[16],数学模型变为
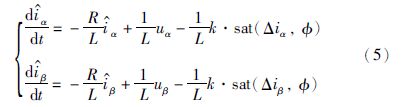
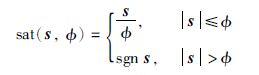
在边界层外采用常规的滑模控制,在边界层内采用连续状态的反馈控制,此时滑模存在的条件为

用式(5)减去式(1)可得:
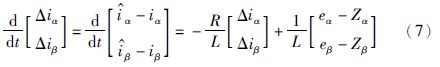
根据滑模控制理论和等价控制原理,如果系统进入滑动模态控制,即估计偏差在滑模面上s=$\dot{s}$=0可得:
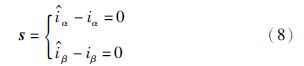
将式(8)代入式(7)可得:
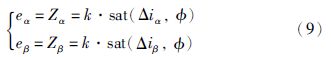
开关信号经过低通滤波后可得到如下的反电动势:
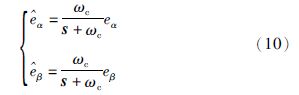
根据反电势与电机磁极位置的关系可以得到磁极位置的估计值${\hat{\theta }}$,进而得到速度估计值${\hat{\omega }}$.
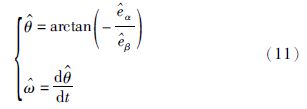
低通滤波器会导致转子位置的相位滞后,因此采用相位补偿来解决这个问题,相位补偿角为

补偿后的估计位置角为

为了推导出滑模存在的条件,首先构造李亚普诺夫函数: V=$\frac{1}{2}$sT·s,滑模存在的条件应满足${\dot{V}}$<0.
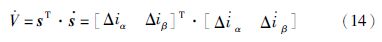
那么可以得到如下公式:
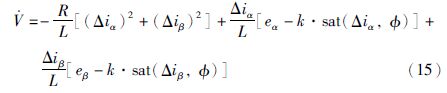
把sat函数值代入可得:
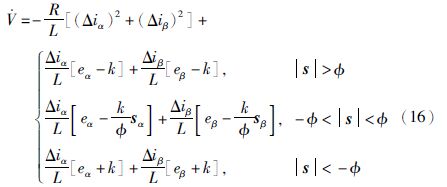
由式(16)选择观测器增益k,当k≥max(|eα|,|eβ|)时,式(16)不能保证${\dot{V}}$<0,说明在边界层内系统不一定稳定. 因此,滑模观测器估算的电流不能最终收敛于实际值. 为了抑制抖动并增加滑模面的趋近快速性,引入模糊边界层调节器.
3 模糊边界层调节器设计模糊控制器时不需要建立被控对象的数学模型,同时适用于永磁同步直线电机多变量,非线性时变、 滞后系统的控制且鲁棒性强的系统. 本文根据经验,通过设计模糊滑模逻辑规则实现模糊滑模观测器,控制目标从跟踪电流误差转化为滑模函数,同时将饱和函数sat(s,$\phi $)代替符号函数sgn s引入滑模边界层,并在边界层之内采用切换控制,使系统快速趋于滑动模态; 在边界层之外,采用反馈控制,以降低在滑动模态快速切换时产生的抖振[16]. 采用边界层削弱抖振时,如果边界层过窄,高频抖振效果不明显; 如果过宽,就会出现较大的稳态误差,因此边界层的宽度对系统的稳定性起关键性的作用.
模糊控制器的输入不是(e,${\dot{e}}$)而是(s,${\dot{s}}$),输出为边界层$\phi $,通过设计规则实现滑模面s为0. 根据控制器的设计步骤,将滑模面进行模糊划分,输入变量的论域为{6,5,4,3,2,1,0,1,2,3,4,5,6},语义变量为{NB,NM,NS,ZR,PS,PM,PB},它们分别代表: “负大,负中,负小,零,正小,正中,正大”; 输出变量的论域为{-2,-1,0,1,2},语义变量为{B,BM,ZE,SM,S},分别代表“大,较大,几乎不变,较小,小”. 制定模糊调节边界层规则要具有对称性,模糊规则如表 1所示. 当|s|较大时,系统远离滑模面,此时趋近运动应该比较剧烈(式(7)即趋近率应该较大),需要增大Φ,使eα和Zα之间的差值增大; 当|s|较小时,系统处于趋向滑模面,这时的趋近运动比较缓和,趋近率相对较小. 在系统趋向和远离滑模面过程中,根据实际情况实时动态调整边界层宽度,从而使趋近率随着电流误差绝对值的大小变化而变化,同时兼顾去抖振和控制精度,以使转速估计性能达到最佳.
| s/${\dot{s}}$ | PB | PM | PS | ZR | NS | NM | NB |
| PB | S | ZE | BM | ZE | SM | B | ZE |
| PM | ZE | S | BM | BM | ZE | SM | B |
| PS | BM | BM | S | S | BM | ZE | SM |
| ZR | ZE | BM | S | S | BM | BM | ZE |
| NS | SM | ZE | BM | BM | S | BM | BM |
| NM | B | SM | ZE | BM | BM | S | ZE |
| NB | ZE | B | SM | ZE | BM | ZE | S |
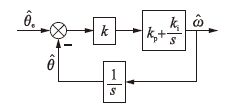
由式(10)~式(13)可以算出转子位置角和速度,但是由于模糊滑模观测器并不能彻底清除抖振现象,再加上低通滤波器带来的相位滞后、 引入幅值的衰减和反电势受外界干扰等因素,很难保证转角估算效果. 这种利用反正切函数直接估计转子位置的方法就变得不可靠了[17, 18],所以引入锁相环估计转子速度和位置[19]. 简化的锁相环系统如图 1所示.
|
| 图 1 简化的锁相环结构 Fig. 1 The sample phase-locked loop structure |
图 1中,k=${\hat{\omega }}$ψf,锁相环的传递函数为
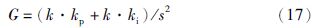
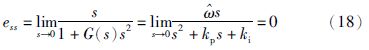
根据以上设计的滑模观测器,可以构建如图 2所示的PMLSM无传感器控制系统,该控制系统内环采用直轴电流id=0的电压空间矢量控制,电流控制器和速度控制器都采用PI控制,其中速度反馈信号和旋转坐标变换角度来自滑模估计模块. PMLSM矢量控制调速系统仿真模型各模块的构建方法见文[20]. 基于sat函数模糊滑模观测器仿真模块如图 3所示. 仿真采用PMLSM参数为R=2.65Ω,L=2.67mH,速度为600mm/s,滑模系数按照滑模存在条件设为10000,滤波器截至频率设为180kHz.
|
| 图 2 PMLSM无传感器控制系统 Fig. 2 Sensorless control system of PMLSM |
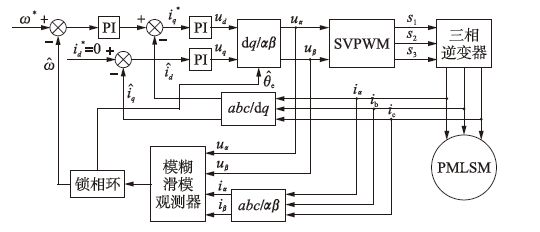
|
| 图 3 模糊滑模观测器结构简图 Fig. 3 The structure diagram of fuzzy sliding mode observer |
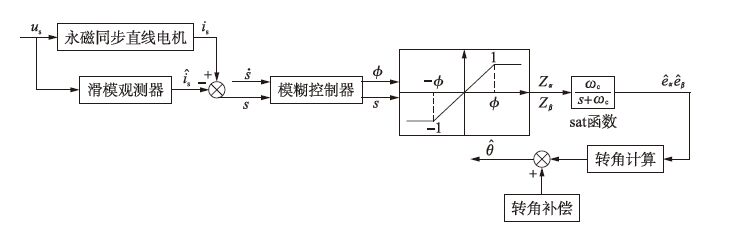
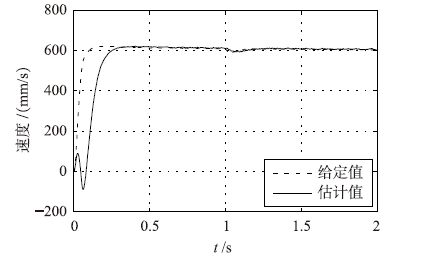
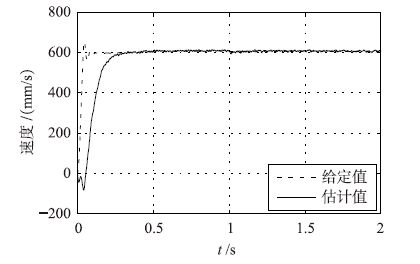
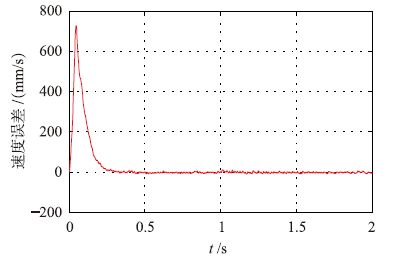
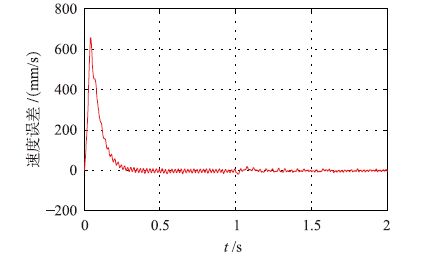
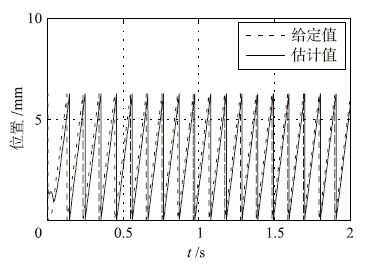
仿真结果如图 4~图 8所示. 图 4和图 5分别为传统的滑模观测器和模糊滑模观测器的速度估计结果,图 6和图 7分别为两者的速度估计误差结果. 将图 4~图 7对比可知,系统消除了滑模抖振且系统响应速度加快. 仿真研究时,反馈量分别是通过模糊滑模观测器和传统滑模观测器估计值进行调速系统反馈,图 8为位置估计结果. 由仿真结果可知,在模糊滑模观测器情况下,电机起动瞬间速度估计误差为1%,而稳态时估计误差为0.06%; 在传统滑模观测器情况下,电机起动瞬间速度估计误差为1.2%,而稳态时估计误差为0.08%. 另外,仿真结果表明采用带有边界层的sat函数代替符号函数,系统的响应速度有了明显提高.
|
| 图 4 传统滑模观测器速度估计结果 Fig. 4 Speed estimation results of traditional sliding mode observer |
|
| 图 5 模糊滑模观测器速度估计结果 Fig. 5 Speed estimation results of fuzzy sliding mode observer |
|
| 图 6 传统滑模观测器速度估计误差 Fig. 6 Speed estimation errors of traditional sliding mode observer |
|
| 图 7 模糊滑模观测器速度估计误差 Fig. 7 Speed estimation errors of fuzzy sliding mode observer |
|
| 图 8 模糊滑模观测器位置估计结果 Fig. 8 Position estimation results of fuzzy sliding mode observer |
本文在PMLSM滑模观测器的基础上,构建了PMLSM调速系统的速度和位置模糊滑模观测器,并利用带有边界层的sat函数,使系统快速达到滑模面. 一定程度上加快了响应速度和削弱了滑模抖振问题,并且提高鲁棒稳定性. 该系统能够快速、 精确地估计出电机速度和磁极位置,从而实现高性能的PMLSM无速度传感器控制.
| [1] | 汪木兰, 张崇巍, 林健, 等. 数控机床用直线电机伺服试验平台开发及应用[J]. 中国机械工程, 2012, 23(3): 274-278. Wang M L, Zhang C W, Lin J, et al. Development of an experimental platform for linear motors in CNC machine tools[J]. China Mechanical Engineering, 2012, 23(3): 274-278. |
| [2] | 石忠东, 王先逵, 陈定积. 永磁交流电动机直接驱动伺服控制技术[J]. 微特电机, 2002, 30(3): 8-10. Shi Z D, Wang X K, Chen D J. Permanent magnet linear synchronous motors direct-drive servo control[J]. Small & Special Electrical Machines, 2002, 30(3): 8-10. |
| [3] | 赵希梅, 郭庆鼎. 基于扰动观测器和重复控制器的永磁直线同步电动机鲁棒控制[J]. 中国电机工程学报, 2010, 30(15): 64-69. Zhao X M, Guo Q D. Robust control based on the disturbance observer and repetitive controller for permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2010, 30(15): 64-69. |
| [4] | 闫光亚, 艾武, 陈冰, 等. 永磁直线同步电机ADRC控制系统[J]. 电工技术学报, 2011, 26(9): 60-66. Yan G Y, Ai W, Chen B, et al. PMLSM active disturbance rejection control[J]. Transactions of China Electro technical Society, 2011, 26(9): 60-66. |
| [5] | Elbuluk M, Li C S. Sliding mode observer for wide-speed sensorless control of PMSM drives[C]//2003 Industry Applications Conference. Piscataway, NJ, USA: IEEE; 2003: 480-485. |
| [6] | Genduso F, Miceli R, Rando C. Back EMF sensorless-control algorithm for high-dynamic performance PMSM[J]. IEEE Transactions on Industrial Electronics, 2010, 57(6): 2092-2100. |
| [7] | 王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 北京: 机械工业出版社, 2009. Wang C Y, Xia J K, Sun Y B. Modern motor control technology[M]. Beijing: China Machine Press, 2009. |
| [8] | 陈长龙, 樊贝, 胡堃, 等. 永磁同步电动机新型滑模观测器无传感器控制[J]. 微特电机, 2013, 41(3): 44-47. Chen C L, Fan B, Hu K, et al. Sensorless control using a novel sliding mode observer for PMSM speed control system[J]. Small & Special Electrical Machines, 2013, 41(3): 44-47. |
| [9] | 陈广辉, 曾敏, 魏良红. 无位置传感器永磁同步电动机矢量控制系统综述[J]. 微特电机, 2011, 39(12): 64-67, 75. Chen G H, Zeng M, Wei L H. Review of sensorless vector control of PMSM[J]. Small & Special Electrical Machines, 2011, 39(12): 64-67, 75. |
| [10] | 王正, 王一平. 基于滑模观测器的PMSM无速度传感器研究[J]. 微电机, 2012, 45(5): 52-54. Wang Z, Wang Y P. Speed sensorless research of permanent magnet synchronous motor based on sliding mode observer[J]. Micromotors, 2012, 45(5): 52-54. |
| [11] | Liu J, Wang G, Yu J S. A study of SMO buffeting elimination in sensorless control of PMSM[C]//2010 8th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2010: 4948-4952. |
| [12] | 张剑, 温旭辉. 一种低成本永磁同步电机高精度转子位置检测方法[J]. 电气传动, 2013, 43(1): 77-80. Zhang J, Wen X H. Research on low-cost approach of high-precision rotor position detection for PMSM[J]. Electric Drive, 2013, 43(1): 77-80. |
| [13] | 贺建军, 段勇, 俞寿益. 基于滑模观测器的SPMSM位置速度估计[J]. 控制工程, 2012, 19(3): 527-530. He J J, Duan Y, Yu S Y. Rotor position and speed estimate of SPMSM using sliding mode estimator[J]. Control Engineering of China, 2012, 19(3): 527-530. |
| [14] | 杨勇, 文丹, 罗安, 等. 基于多目标优化的模糊滑模变结构控制及应用[J]. 中南大学学报, 2006, 37(6): 1149-1154. Yang Y, Wen D, Luo A, et al. Fuzzy sliding mode variable structure control based on multi-objective optimization and its application[J]. Journal of Central South University Science and Technology, 2006, 37(6): 1149-1154. |
| [15] | 周元钧, 蔡名飞. 改进的永磁同步电机转子初始位置检测方法[J]. 电机与控制学报, 2010, 14(3): 68-72. Zhou Y J, Cai M F. Initial rotor position inspection of PMSM based on rotating high frequency voltage signal injection[J]. Electric Machines and Control, 2010, 14(3): 68-72. |
| [16] | 刘金坤. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005. Liu J K. MATLAB simulation for sliding mode control[M]. Beijing: Tsinghua University Press, 2005. |
| [17] | Paponpen K, Kongghirun M. An improved sliding mode observer for speed sensorless vector control drive of PMSM[C]//Proceedings of CES/IEEE 5th International Power Electronics and Motion Control Conference. Piscataway, NJ, USA: IEEE, 2006: 1-5. |
| [18] | 刘家曦, 李铁才, 杨贵杰. 永磁同步电机转子位置与速度预估[J]. 电机与控制学报, 2009, 13(5): 690-694. Liu J X, Li T C, Yang G J. Rotor position and speed estimation for PMSM[J]. Electric Machines and Control, 2009, 13(5): 690-694. |
| [19] | 鲁文其, 胡育文, 杜栩杨, 等. 永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J]. 中国电机工程学报, 2010, 30(33): 78-83. Lu W Q, Hu Y W, Du X Y, et al. Sensorless vector control using a novel sliding mode observer for PMSM speed control system[J]. Proceedings of the CSEE, 2010, 30(33): 78-83. |
| [20] | 陆华才. 无位置传感器永磁直线同步电机进给系统初始位置估计及控制研究[D]. 杭州: 浙江大学, 2008. Lu H C. Position sensorless control strategy and initial position estimation of permanent magnet linear synchronous motor feeding system[D]. Hangzhou: Zhejiang University, 2008. |



