2. 油气藏地质及开发工程国家重点实验室·西南石油大学, 四川 成都 610500;
3. 中海油研究总院, 北京 朝阳 100028
2. State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. CNOOC Research Institute, Chaoyang, Beijing 100028, China
深水蕴藏着丰富的油气资源,以中国南海为例,其油气储量约为中国油气总储量的33%[1]。但由于井筒环境的恶劣和作业环境的苛刻阻碍了深水油气资源的大规模开发。其中,环空圈闭压力问题是深水油气资源开发过程中,引起套管失效,威胁井筒安全的主要问题之一[2]。产生环空圈闭压力的原因主要是井底高温流体在生产过程中流至井口,通过多层套管传热至环空圈闭中,造成密闭环空流体热膨胀,从而使得环空压力升高[3]。在陆地及浅水油气井中,可通过井口设备将压力释放。但在深水油气井中,由于水下测试树和采油树的设备限制,只能对油管与生产套管之间的环空压力进行泄压[4]。如果没有有效的治理措施,将造成套管挤毁、破裂等重大井下事故[5-6]。通常的环空圈闭压力治理技术主要包括水泥返至套管鞋以下、真空隔热油管、提高管材钢级和壁厚、全封固井、氮气泡沫水泥浆隔离液、可压缩复合泡沫和破裂盘。其中,破裂盘安装方便,使用成本较低,在现场作业中应用广泛[7-9]。破裂盘通常由破裂片和夹持器组成[10],当破裂片两侧压差达到额定压力时,破裂片即打开,以平衡两端压力,从而达到保护套管确保井筒安全的目的[11]。而破裂片又分为正拱型和反拱型,由高压端向低压端挤破,因此,在阀值设定时,需考虑由内向外和由外向内等不同方向的压力值。由于该技术被国外垄断和保密,研究基于破裂盘技术的圈闭压力治理机理对国产技术的开发以及中国深水油气安全开采具有重要意义。
环空圈闭压力的准确预测方法是评估破裂盘治理效果的基础。国外对环空圈闭压力的研究起步较早,Halal等明确指出,环空圈闭压力的计算应该考虑径向热传递的影响[12];Oudeman等建立了密闭环空压力通用预测模型以及漏失影响的未密闭环空压力通用预测模型[13];Hasan等在此基础上提出了两种解析模型,包括拟稳态传热和瞬态传热[14]。国内方面,高宝奎考虑流体热膨胀效应以及体积压缩效应,得到套管附加载荷计算模型[15];车争安等在此基础上,得到温度引起的附加载荷与环空压力之间的关系[16];邓元洲等考虑压力体积耦合变化,通过迭代法得到环空温度变化引起的压力变化[17];杨进等基于深水结构及传热规律,建立了深水套管环空压力的预测模型[18];张百灵等结合现场实例对基于PVT状态方程和胡克定律模型计算环空压力进行了对比[19],结果表明,基于PVT状态方程考虑温度压力耦合作用的环空压力预测模型更适用于深水井筒环空压力预测。张波等引入产量及生产时间对环空圈闭压力的影响,发现生产初期,环空圈闭压力上升较快,产量越高,环空圈闭压力越大[20]。随后,张波等研究了流体特性对环空圈闭压力的影响[21],结果表明,环空压力随环空液体膨胀压缩系数减小而减小,随着产出液比热容和产量增加而增加,发现环空压力与产出液井底温度的线性关系,可通过产出液井口温度得到环空压力大小。周波等建立了基于拟稳态传热过程的环空圈闭压力模型[22],通过环空注氮对环空压力控制进行了模拟,表明了环空注氮对环空圈闭压力治理的有效性。
目前,基于拟稳态传热原理和PVT方程的压力预测方法形成了快速准确的环空圈闭压力预测模型,但缺乏圈闭压力治理效果的模拟研究。为此,针对深水油气井多层环空的特点,在环空圈闭压力预测模型的基础上提出了适用于深水井多环空的压力预测模型,并结合破裂盘技术,提出破裂盘的阀值确定方法,从而实现环空圈闭压力的控制与治理。通过模拟西非的深水油气井环空圈闭压力治理过程,表明了破裂盘技术的可行性。
1 井筒流体温度分布模型图 1为典型深水油气井的井身结构。
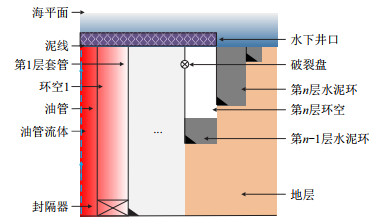 |
| 图1 深水油气井井身结构示意图 Fig. 1 Schematic diagram of well structure in deep water wells |
井底流体在流向井口的过程中,高温流体与地层及环空存在温度差,通过热传导、热对流及热辐射传递热量。基于Hasan环空圈闭压力预测模型[3],假设如下:(1)流体在井筒中作一维稳定流动;(2)只考虑径向热传递,不考虑轴向热传递;(3)井筒垂直且各层套管及油管居中;(4)热量由井筒至水泥环外边缘为稳态传热,由水泥环外边缘至地层为非稳态传热。
由能量守恒定律可知,高温流体在由井底流向井口的过程中,井底携带的热量分别沿轴向和径向传递。径向上的热传递被视为拟稳态过程,通过无因次地层导热时间函数
| $ \dfrac{\partial {{T}_{\rm f}}\left( z, t \right)}{\partial z}-A\left( t \right){{T}_{\rm f}}\left( z, t \right)+A\left( t \right){{T}_{\rm e}}\left( z \right)=0 $ | (1) |
| $ A\left( t \right)=\dfrac{2 {\rm \pi} {{r}_{\rm to}}{{U}_{\rm to}}{{k}_{\rm e}}}{{{w}_{\rm q}}{{c}_{\rm p}}\left[ {{k}_{\rm e}}+f\left( t \right){{r}_{\rm to}}{{U}_{\rm to}} \right]} $ | (2) |
| $ {{U}_{\rm to}}^{-1}= \dfrac{{{r}_{\rm to}}}{{{r}_{\rm ti}}{{h}_{\rm f}}}+\dfrac{{{r}_{\rm to}}\ln \left( {{{r}_{\rm to}}}/{{{r}_{\rm ti}}}\; \right)}{{{k}_{\rm t}}}+\sum\limits_{ k=1}^{\lambda }\dfrac{1}{{{h}_{{\rm c}, k}}+{{h}_{{\rm r}, k}}}+ \\{\kern 40pt}\sum\limits_{ k=1}^{\lambda }{\dfrac{{{r}_{\rm to}}\ln \left( {{{r}_{{\rm co}, k}}}/{{{r}_{{\rm ci}, k}}}\; \right)}{{{k}_{{\rm c}, k}}}+\dfrac{{{r}_{\rm to}}\ln \left( {{{r}_{\rm h}}}/{{{r}_{{\rm co}, k}}} \right)}{{{k}_{\rm cem}}}} $ | (3) |
式中:
下标
引入边界条件
| $ {{T}_{\rm f}}\left( 0 \right)={{T}_{\rm bh}} $ | (4) |
| $ {{T}_{\rm e}}\left( z \right)={{T}_{\rm bh}}-{{g}_{\rm e}}z $ | (5) |
式中:
对式(1)进行求解,并代入边界条件可得任意深度的流体温度
| $ {{T}_{\rm f}}\left( z, t \right)={{T}_{\rm bh}}+{{g}_{\rm e}}z+\dfrac{{{g}_{\rm e}}}{A(t)}-\dfrac{{{g}_{\rm e}}}{A(t)}{\rm e}^{ -A\left( t \right)z } $ | (6) |
由能量守恒定律可知,环空流体传递至水泥环外缘的热量与井筒流体传至水泥环外缘的热量相等,由此可得到第
| $ {{T}_{{\rm a}, k}}\left( z, t \right)\!=\!\dfrac{{{r}_{\rm to}}{{U}_{\rm to}}\ln \left( {{{r}_{\rm h}}}/{{{r}_{{\rm co}, k}}} \right)\left[ {{T}_{\rm f}}\left( z, t \right)-{{T}_{\rm h}}\left( z, t \right) \right]}{{{k}_{\rm e}}} + \\ {\kern 40pt} {{T}_{\rm h}}\left( z, t \right) $ | (7) |
式中:
由于工艺限制,水泥在上返过程中未能返至井口,在井口与水泥环封固位置将形成一段环空自由带。在生产测试过程中,油管中的高温流体沿管柱及套管间的流体向各环空中传递热量。环空中的密闭流体受热膨胀,致使环空圈闭压力升高。增加的环空压力是变化的体积与温度的函数,即PVT状态方程。对PVT方程求偏微分可得第
| $ \Delta {{p}_{{\rm a}, k}}\left( t \right)=\dfrac{{{\alpha }_{{\rm 1}, k}}}{{{\kappa }_{{\rm T}, k}}}\Delta {{\overline{T}}_{{\rm a}, k}}\left( t \right)-\dfrac{1}{{{\kappa }_{{\rm T}, k}}{{V}_{k}}}\Delta {{V}_{k}}\left( t \right)+\\ {\kern 40pt}\dfrac{1}{{{\kappa }_{{\rm T}, k}}{{V}_{{\rm f}, k}}}\Delta {{V}_{{\rm f}, k}}\left( t \right) $ | (8) |
| $ \Delta {{\overline{T}}_{{\rm a}, k}}\left( t \right)=\dfrac{\int_{{{z}_{{\rm toc}, k}}}^{h}{{{T}_{{\rm a}, k}}\left( z, t \right){\rm d}z-\int_{ {{z}_{{\rm toc}, k}}}^{h}{{{T}_{\rm e}}\left( z \right){\rm d}z}}}{h-{{z}_{{\rm toc}, k}}} $ | (9) |
式中:
假设环空密闭,环空微元段流体体积变化为0,即
环空体积的变化
| $ \Delta {{V}_{k}}=-\Delta {{V}_{1, k}}+\Delta {{V}_{2, k}}+\Delta {{V}_{3, k}}-\Delta {{V}_{4, k}} $ | (10) |
其中
| $ \begin{array}{l} \Delta {{V}_{1, k}}={\rm \pi} \left[ {{\left( {{r}_{{\rm co, }k}}+{{u}_{1, k}} \right)}^{2}}-{{r}_{{\rm co, }k}}^{2} \right] \end{array} $ | (11) |
| $ \begin{array}{l} \Delta {{V}_{2, k}}={{\alpha }_{{\rm l}, k}}\Delta \overline{{{T}_{k}}}\left( t \right){\rm \pi} \left[ {{r}_{{\rm ci}, (k+1)}}^{2}-{{r}_{{\rm co, }k}}^{2} \right] \end{array} $ | (12) |
| $ \begin{array}{l} \Delta {{V}_{3, k}}\!=\!{\rm \pi} \left[ {{\left( {{r}_{{\rm co, }k}}+{{u}_{1, k}} \right)}^{2}}\!-\!{{\left( {{r}_{{\rm co, }k}}+{{\mu}_{1, k}}\!-\!{{\mu}_{2, k}} \right)}^{2}} \right] \end{array} $ | (13) |
| $ \begin{array}{l} \Delta {{V}_{4, k}}=\dfrac{{\rm \pi} ({{r}_{{\rm ci}, \left( k+1 \right)}}^{2}-{{r}_{{\rm co}, k}}^{2})\Delta {{p}_{{\rm a}, k}}\left( t \right)}{{{E}_{{\rm l}, k}}} \end{array} $ | (14) |
| $ \begin{array}{l} {{u}_{1, k}}={{\alpha }_{\rm s}}\Delta \overline{{{T}_{k}}}\left( t \right)\dfrac{\left( {{r}_{{\rm co, }k}}^{2}-{{r}_{{\rm ci, }k}}^{2} \right)\left( 1+\mu \right)}{2{{r}_{{\rm co, }k}}\left( 1-\mu \right)} \end{array} $ | (15) |
| $ \begin{array}{l} {{u}_{2, k}}=\dfrac{{{r}_{{\rm co}, \left( k-1 \right)}}\Delta {{p}_{{\rm a}, k}}\left( t \right)\left( 1+\mu \right)}{{{E}_{\rm t}}\left( {{r}_{{\rm co, }k}}^{2}-{{r}_{{\rm ci, }k}}^{2} \right)} \cdot \\ {\kern 40pt}\left[ {{r}_{{\rm ci, }k}}^{2}+2\left( 1-2\mu \right){{r}_{{\rm co, }k}}^{2} \right] \end{array} $ | (16) |
式中:
环空压力和体积的耦合影响可通过迭代法进行求解[17]。假定迭代初值代入式(11)
综合考虑泄压工具在深水井井下的实际工况(钻井、完井和生产泄压),破裂盘的阀值设定需要确保在钻完井过程中,破裂盘关闭,防止误操作而打开,同时在生产过程中,根据套管受力状态,打开破裂盘,保护套管安全,即泄压阀值主要取决于相邻的内层和外层套管强度。同时,破裂盘通过高低压端的压差来实现工作,因此需要确定由内向外和由外向内两个方向的阀值确定方法。
对于由内向外打开,破裂盘打开阀值为
| $ \begin{array}{l} {\max}\left( {{p}_{\rm cm}}, {{p}_{\rm pt}}, {{p}_{\rm gk}} \right)<{\rm }{{p}_{\rm v{\rm o}}}<{{{p}_{\rm b}}}/{{{S}_{\rm b}}}\; \end{array} $ | (17) |
其中
| $ \begin{array}{l} {{p}_{\rm pt}}= {{p}_{\rm b}}\times 60\% \end{array} $ | (18) |
| $ \begin{array}{l} {{p}_{\rm cm}}{\rm =}{{p}_{\rm ri}}+{{p}_{\rm ro}}+\Delta {{p}_{\rm f}}+{{p}_{\rm bump}} \end{array} $ | (19) |
| $ \begin{array}{l} {{p}_{\rm gk}}={{p}_{\rm f}}-{{\rho }_{\rm g}}{\rm g}{{z}_{\rm g}} \end{array} $ | (20) |
式中:
g—重力加速度,g = 9.81 m/s
对于由外向内打开,破裂盘打开阀值为
| $ \begin{array}{l} {{p}_{\rm e}}<{\rm }{{p}_{\rm vi}}<{{{p}_{\rm c}}}/{{{S}_{\rm c}}}\; \end{array} $ | (21) |
其中
| $ \begin{array}{l} {{p}_{\rm e}}{\rm =}{{\rho }_{\rm f}}{\rm g}\alpha {{L}_{\rm c}} \end{array} $ | (22) |
式中:
对西非海域某高温高产油井[20]的环空圈闭压力现象进行模拟,井身结构如图 2所示。利用表 1中参数对该井在120 t/d稳定生产200 d后的环空温度分布及环空压力变化进行计算。表 2的套管强度参数用于套管安全校核。表 3中钻井工况参数用于泄压阀值的确定。
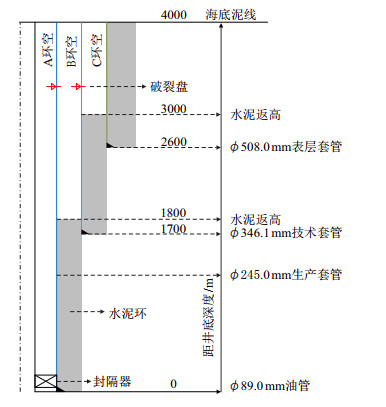 |
| 图2 西非油井井身结构 Fig. 2 Well structure of deep water wells in West Africa |
| 表1 井筒物性参数表 Tab. 1 Physical property parameters of wellbore |
| 表2 西非油井套管强度参数表 Tab. 2 Strength parameters of oil well casing in West Africa |
| 表3 钻井作业工况参数 Tab. 3 Drilling parameters of operation conditions |
图 3为深水油气井以120 t/d的产量生产200 d后的井筒温度分布。在深水油气开采过程中,油管流体在开采过程中将井底采出的热量,受到地温梯度的影响,采出的温度随着深度逐渐降低。径向上,油管流体将热量传递至各个环空,由于A环空离油管流体最近,获得热量最多,环空温度最高,B环空温度其次,C环空温度最低。环空温度的上升是造成环空圈闭压力的主要原因。
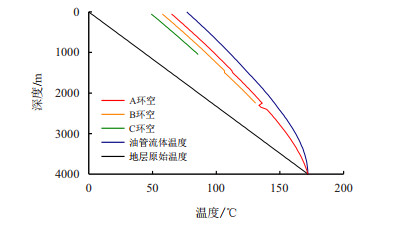 |
| 图3 深水油气井温度分布 Fig. 3 Temperature distribution of deep water oil and gas wells |
图 4为环空圈闭压力预测结果。以120 t/d的产量对环空圈闭压力上升规律进行模拟,随着生产的进行,环空流体随着温度的增加,产生热膨胀效应,从而环空压力上升。在生产初期,各环空温度增加较快,进而导致环空压力上升剧烈。生产20 d后,环空温度和压力增长幅度相对较低。
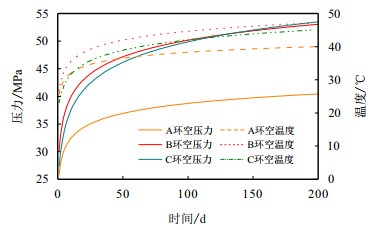 |
| 图4 环空圈闭压力模拟 Fig. 4 Simulation of annulus trap pressure |
在生产作业中,套管抗内压额定安全系数取1.250,套管抗外挤额定安全系数取1.125。在套管的校核过程中,套管安全系数越大,套管越安全。分别考虑正常作业和A环空泄压或者排出的特殊工况进行套管强度校核。
(1) 正常作业
考虑到B、C环空压力相近,环空间的技术套管压差始终处于一个近平衡的状态,因此仅对生产套管和表层套管进行校核。图 5为套管强度校核结果。
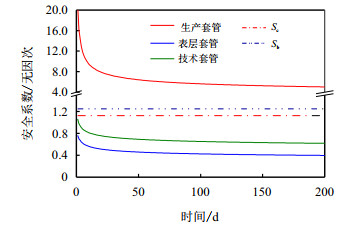 |
| 图5 正常作业下的套管强度校核 Fig. 5 Casing strength check under normal operation |
从图 5中可以看出,生产套管在生产过程中始终保证了安全。但表层套管在生产开始的阶段即存在破裂的风险,需要采取环空圈闭压力治理措施保障井筒的安全。
(2) A环空泄压或掏空
由于A环空是唯一与深水井口管线相连的环空,存在泄压作业或者环空液体排出的情况。图 6为A环空进行泄压或者掏空情况下的套管强度校核结果。
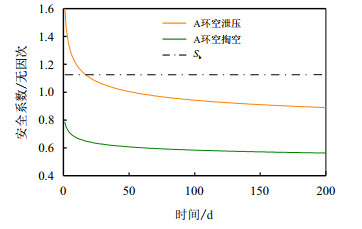 |
| 图6 特殊工况下的生产套管强度校核 Fig. 6 Strength check of production casing under special working condition |
对A环空进行泄压后,由于B环空压力的增加,生产套管的安全系数逐渐降低,在生产17 d后,生产套管存在被挤毁的风险。对于A环空掏空后,生产套管除了受到B环空圈闭压力上升的挤压,还受到液柱压力的作用,在生产开始阶段,套管就可能被挤毁。
3.3 圈闭压力泄压效果模拟通过两种工况的模拟可知,表层套管和技术套管均存在被胀破的风险。为保护井筒安全,分别在表层套管和技术套管安装由内向外泄压的破裂盘。由于生产套管作为井筒隔绝地层的最后一道屏障,通常保障生产套管的完整性,可通过调节A环空压力保障井筒环空压力安全。
(1) 环空圈闭压力治理阀值
根据破裂盘打开阀值的确定方法,结合钻完井工况,得到破裂盘打开阀值的范围,从而进一步确定技术套管和表层套管的打开阀值,如表 4所示。
| 表4 套管泄压阀值 Tab. 4 Casing pressure relief threshold |
(2) 环空圈闭压力治理效果
根据井筒压力预测结果,需在技术套管和表层套管安装向外泄压的破裂盘。由于套管强度在生产第一天超过负荷,破裂盘已打开,套管压差为0,技术套管和表层套管处于安全状态。同时,对破裂盘打开后的生产套管强度进行校核,校核结果如图 7所示。A环空掏空,生产套管外挤力校核比较安全,正常生产情况下,A环空需在17 d进行泄压,则可保证套管内压安全。
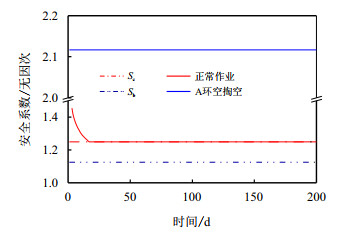 |
| 图7 破裂盘泄压效果模拟 Fig. 7 Simulation of pressure relief effect of rupture disc |
(1) 结合深水环空圈闭压力产生机理,考虑多层套管的传热过程以及环空压力与体积的耦合效应,建立了深水井筒多层环空的环空圈闭压力预测模型。
(2) 基于深水破裂盘的工作原理,建立了由内向外以及由外向内两个方向破裂盘打开的确定方法。
(3) 对深水油气开采过程进行模拟,模拟结果表明,在正常作业中,技术套管和表层套管存在被胀破的风险,在A环空泄压或套管的情况下,生产套管存在挤毁风险。
(4) 对安装破裂盘后的深水井筒套管进行校核,在正常作业和特殊工况下套管均处于安全状态。因此,破裂盘可有效实现环空圈闭压力的治理,保障深水油气井的安全开采。
| [1] |
吴秀平, 王金平, 刘燕飞. 国际深水油气资源研究竞争力态势的文献计量分析[J]. 世界科技研究与发展, 2017, 39(2): 209-216. WU Xiuping, WANG Jinping, LIU Yanfei. Bibliometric analysis of competitive situation of international deepwater oil and gas resources research[J]. World Sci-Tech R & D, 2017, 39(2): 209-216. doi: 10.16507/j.issn.1006-6055.2016.11.002 |
| [2] |
BRADFORD D W, GIBSON D H, GOSCH S W, et al. Marlin failure analysis and redesign; Part 1, Description of failure[C]. SPE 74528-MS, 2012. doi: 10.2118/74528-MS
|
| [3] |
HASAN R, IZGEC B, KABIR S, et al. Sustaining production by managing annular-pressure buildup[J]. SPE Production & Operations, 2010, 25(2): 195-203. doi: 10.2118/120778-PA |
| [4] |
American Petroleum Institute. API R90: Management of sustained casing pressure on offshore wells[S]. Washington, USA, American Petroleum Institute, 2016.
|
| [5] |
ROCHA-VALADEZ T, HASAN A R, MANNAN S, et al. Assessing wellbore integrity in sustained-casing-pressure annulus[J]. SPE Drilling & Completion, 2014, 29(1): 131-138. doi: 10.2118/169814-PA |
| [6] |
OUDEMAN P, KEREM M. Transient behavior of annular pressure build-up in HP/HT wells[J]. SPE Drilling & Completion, 2006, 21(4): 234-241. doi: 10.2118/88735-PA |
| [7] |
胡伟杰, 王建龙, 张卫东. 深水钻井密闭环空圈闭压力预测及释放技术[J]. 中外能源, 2012, 17(8): 41-45. HU Weijie, WANG Jianlong, ZHANG Weidong. Confined annular trap pressure prediction and release technology for deep water drilling[J]. Sino-Global Energy, 2012, 17(8): 41-45. |
| [8] |
DONG Guangjian, CHEN Ping. A review of the evaluation methods and control technologies for trapped annular pressure in deepwater oil and gas wells[J]. Journal of Natural Gas Science and Engineering, 2017, 37: 85-105. doi: 10.1016/j.jngse.2016.11.042 |
| [9] |
LIU Z, SAMUEL R, GONZALES A, KANG Y. Modeling and simulation of annular pressure buildup (APB) mitigation using rupture disk[C]. SPE 178807-MS, 2016. doi: 10.2118/178807-MS
|
| [10] |
熊爱江, 杨进, 宋宇, 等. 油气井用破裂盘测试与破裂压力模型研究[J]. 压力容器, 2017, 34(8): 1-6. XIONG Aijiang, YANG Jin, SONG Yu, et al. Research on model of fracture pressure on test of oil and gas burst disc[J]. Pressure Vessel Technology, 2017, 34(8): 1-6. doi: 10.3969/j.issn.1001-4837.2017.08.001 |
| [11] |
黄小龙, 严德, 田瑞瑞, 等. 深水套管环空圈闭压力计算及控制技术分析[J]. 中国海上油气, 2014, 26(6): 61-65. HUANG Xiaolong, YAN De, TIAN Ruirui, et al. Research on calculation of casing annulus trapped pressure and its control techniques for deep water well[J]. China Offshore Oil and Gas, 2014, 26(6): 61-65. |
| [12] |
HALAL A S, MITCHELL R F. Casing design for trapped annular pressure buildup[J]. SPE Drilling & Completion, 1994, 9(2): 107-114. doi: 10.2118/25694-PA |
| [13] |
OUDEMAN P, BACARREZA L J. Field trial results of annular pressure behavior in a high-pressure/hightemperature well[J]. SPE Drilling & Completion, 1995, 10(2): 84-88. doi: 10.2118/26738-PA |
| [14] |
HASAN A R, IZGEC B, KABIR C S. Ensuring sustained production by managing annular-pressure buildup[C]. SPE 121754-MS, 2009. doi: 10.2118/121754-MS
|
| [15] |
高宝奎. 高温引起的套管附加载荷实用计算模型[J]. 石油钻采工艺, 2002, 24(1): 8-10. GAO Baokui. Practical model for calculating the additional load on casing by high temperature[J]. Oil Drilling & Production Technology, 2002, 24(1): 8-10. doi: 10.3969/j.issn.1000-7393.2002.01.003 |
| [16] |
车争安, 张智, 施太和, 等. 高温高压含硫气井环空流体热膨胀带压机理[J]. 天然气工业, 2010, 30(2): 88-90. CHE Zheng'an, ZHANG Zhi, SHI Taihe, et al. Mechanism of annular fluid thermal expansion pressure in HTHP sour gas wells[J]. Natural Gas Industry, 2010, 30(2): 88-90. doi: 10.3787/j.issn.1000-0976.2010.02.023 |
| [17] |
邓元洲, 陈平, 张慧丽. 迭代法计算油气井密闭环空压力[J]. 海洋石油, 2006, 26(2): 93-96. DENG Yuanzhou, CHEN Ping, ZHANG Huili. Calculating the pressure in sealed annulus in oil well by iterative method[J]. Offshore Oil, 2006, 26(2): 93-96. doi: 10.3969/j.issn.1008-2336.2006.02.019 |
| [18] |
杨进, 唐海雄, 刘正礼, 等. 深水油气井套管环空压力预测模型[J]. 石油勘探与开发, 2013, 40(5): 616-619. YANG Jin, TANG Haixiong, LIU Zhengli, et al. Prediction model of casing annulus pressure for deepwater well drilling and completion operation[J]. Petroleum Exploration and Development, 2013, 40(5): 616-619. doi: 10.-11698/PED.2013.05.17 |
| [19] |
张百灵, 杨进, 黄小龙, 等. 深水井筒环空压力计算模型适应性评价[J]. 石油钻采工艺, 2015, 37(1): 56-59. ZHANG Bailing, YANG Jin, HUANG Xiaolong, et al. Adaptability evaluation of calculation model of annular pressure of deepwater wellhole[J]. Oil Drilling & Production Technology, 2015, 37(1): 56-59. doi: 10.13639/j.odpt.2015.01.014 |
| [20] |
张波, 管志川, 张琦. 深水油气井开采过程环空压力预测与分析[J]. 石油学报, 2015, 36(8): 1012-1017. ZHANG Bo, GUAN Zhichuan, ZHANG Qi. Prediction and analysis on annular pressure of deepwater well in the production stage[J]. Acta Petrolei Sinica, 2015, 36(8): 1012-1017. doi: 10.7623/syxb201508013 |
| [21] |
张波, 管志川, 胜亚楠, 等. 深水油气井井筒内流体特性对密闭环空压力的影响[J]. 石油勘探与开发, 2016, 43(5): 799-805. ZHANG Bo, GUAN Zhichuan, SHENG Yanan, et al. Impact of wellbore fluid properties on trapped annular pressure in deepwater wells[J]. Petroleum Exploration and Development, 2016, 43(5): 799-805. doi: 10.11698/PED.2016.05.17 |
| [22] |
周波, 杨进, 刘正礼, 等. 深水油气井筒环空注氮控压机理[J]. 石油勘探与开发, 2015, 42(3): 386-389. ZHOU Bo, YANG Jin, LIU Zhengli, et al. Mechanism of pressure management by injecting nitrogen in casing annulus of deepwater wells[J]. Petroleum Exploration and Development, 2015, 42(3): 386-389. doi: 10.11698/PED.2015.03.17 |
| [23] |
HASAN A R, KABIR C S. Heat transfer during two-phase flow in wellbores; Part Ⅰ-Formation temperature[C]. SPE 22866-MS, doi: 10.2118/22866-MS
|
| [24] |
吴雪婷, 王江帅, 冯炜. 深水油气井环空圈闭压力研究[J]. 石油机械, 2018, 46(12): 47-50. WU Xueting, WANG Jiangshuai, FENG Wei. Research on annular pressure buildup in deepwater oil and gas well[J]. China Petroleum Machinery, 2018, 46(12): 47-50. doi: 10.16082/j.cnki.issn.1001-4578.2018.12.009 |
 2020, Vol. 42
2020, Vol. 42


