2. 古勃金国立石油与天然气大学, 俄罗斯 莫斯科 119991
2. National State University of Oil and Gas, Gubkin University, Moscow, 119991, Russia
近年来以致密油气为代表的非常规油气资源成为油气开发领域的热点。相对于常规油气藏,非常规资源储层物性普遍较差,油气规模化经济开发取决于工程技术的进步[1]。以中国致密油藏为例,原油主要聚集于纳微米级孔隙的储集层中,原油品味低、储层非均质性强、地层能量低,一次开发采收率普遍低于10%[2]。目前,长水平井多级分段压裂是致密油藏开发的主要模式[3],该模式虽解决了初期产能问题,但仍存在地层能量递减快,单井产量低等问题,亟需探索中国致密油藏开发中后期增能和提高采收率的方式和方法。
实践证明,向致密储层中注入CO
气体在油藏流体中的扩散系数实验测定方法可分为直接法和间接法[9],直接法由于需要在扩散过程进行实时取样而易对系统平衡造成干扰,影响测定精度,因此,目前大多采用间接法测定扩散系数,即通过测定扩散过程中系统某一参数(压力、体积、密度等)的变化,经过相应转换后得到扩散系数。压力降落法(PVT法)由于测定精度更高以及计算过程简单而被广泛应用。压降法最早由Riazi提出[10],Riazi通过测定PVT筒中系统压力变化及气液界面的移动,结合半解析模型,得到了37.8 ℃和7.1 MPa下甲烷在戊烷中的扩散系数。Zhang等对Riazi的方法进行了改进[11],无需考虑气液界面的移动,并建立了压降拟合计算扩散系数的方法,得到了CO
综上,当前研究存在的主要问题是:(1)研究对象多为气液体相扩散;(2)实验条件与致密油藏条件差距大;(3) CO
本实验所用气体为成都科源气体有限公司提供的纯度为99.9%的商品气CO
| 表1 岩芯物性参数 Tab. 1 Core physical parameters |
实验装置如图 1a所示,主要包括流体注入系统(ISCO泵和CO
 |
| 图1 实验装置示意图和基质—裂缝物理扩散模型 Fig. 1 Schematic diagram of experimental device and matrix-fracture model of diffusion |
图 1b为实验中设计的基质-裂缝物理扩散模型。为了减小注气伊始压力冲击对超临界CO
在扩散系数实验测定过程中,CO
由岩石孔渗测定仪测定岩芯孔隙度和渗透率,根据式(1)计算岩芯迂曲度[16],具体测定结果见表 1。
| $ 2\tau = 1+\dfrac{1}{2\sqrt{1-\phi }}+\\ {\kern 40pt}\sqrt{1-\phi }\dfrac{\sqrt{{{\left( \dfrac{1}{\sqrt{1-\phi }}-1 \right)}^{2}}+\dfrac{1}{4}}}{1-\sqrt{1-\phi }} $ | (1) |
式中:
式(1)为经验公式,计算得到的迂曲度略高。
基于压力降落法测定CO
(1) 按图 1a连接实验装置,实验开始前先对所有管线进行清洗并用高压氮气吹干;由ISCO泵向岩芯夹持器及各个管路中注入高于实验压力3
(2) 将基质岩芯烘干称重,测定孔渗等参数,然后对其进行抽真空饱和油处理后放入岩芯夹持器,并在基质岩芯顶部位置(即岩芯夹持器入口端)放置一块1 cm厚的高渗岩芯片。
(3) 将实验所用CO
(4) 给岩芯夹持器加上高于实验压力3
(5) 打开阀门4和5,将中间容器中的CO
(6) 由压力监测系统实时监测并记录超临界CO
(7) 将实验数据保存好,对实验装置及管路进行清洗拆卸,重复下一组实验。
1.3 扩散系数计算方法本次实验扩散系数的计算基于图 1b所示的物理扩散模型,在此基础上建立相应的数学模型描述超临界CO
(1) 实验所用的基质岩芯为均质、各向同性,且原油在岩芯中均匀分布。
(2) 扩散系数在整个扩散过程中为常数,即不考虑组分浓度对扩散系数的影响。
(3) 忽略原油膨胀及密度变化引起的自然对流影响,只考虑分子扩散过程。
(4) 忽略气液边界的传质阻力,即采用平衡边界条件。
(5) 整个扩散过程体系温度恒定。
(6) 忽略液相的蒸发。
根据Fick扩散定律,同时考虑岩芯物性参数对扩散的影响[12],超临界CO
(1) 扩散偏微分方程
| $ \dfrac{ \partial c(x, t)}{ \partial t}=\dfrac{{{D}_{{\rm eff}}}\tau }{\phi }\dfrac{{{ \partial }^{2}}c(x, t)}{ \partial {{x}^{2}}} $ | (2) |
(2) 初始条件
| $ c\left( x, t \right)=0, {\kern 13pt }t=0, 0\leqslant x\leqslant L $ | (3) |
(3) 边界条件
| $ c\left( x, t \right)={{c}_{\rm eq}}\left( {{p}_{\rm eq}} \right), {\kern 13pt }x=0, t>0 $ | (4) |
| $ \dfrac{ \partial c(x, t)}{ \partial x}=0, {\kern 13pt }x=L, t>0 $ | (5) |
式中:
式(4)、式(5)分别为上下边界条件,其中,上边界(即在高渗岩芯与致密岩芯的交界处)采用平衡边界条件[17],认为界面处的浓度始终为平衡压力下浓度
式(2)
| $ c\left( x, t \right)={{c}_{\rm eq}}-\dfrac{4{{c}_{\rm eq}}}{\mathsf{π} }\sum\limits_{n=0}^{\infty }\, \dfrac{{{(-1)}^{n}}}{2n+1}{{{\rm e}}^{-\frac{{{(2n+1)}^{2}}{{\mathsf{π} }^{2}}}{4{{L}^{2}}}\frac{{\tau{D}_{{\rm eff}}} }{\phi }t}} \cdot \\ {\kern 20pt}{\cos}\dfrac{\left( 2n+1 \right)\mathsf{π} x}{2L} $ | (6) |
由质量守恒定律和真实气体状态方程可知,气相中CO
| $ \dfrac{{{V}_{\rm g}}}{{{Z}_{\rm g}}{\rm R}T}\dfrac{{\rm d}p(t)}{{\rm d}t}=-\dfrac{{{D}_{\rm eff}}\tau }{\phi }A{{\left. \dfrac{ \partial c}{ \partial x} \right|}_{x=0}} $ | (7) |
式中:
R—气体通用常数,R= 8.314 J/(mol
根据式(7)对式(6)进行微分求解
| $ {{\left. \dfrac{ \partial c(x, t)}{ \partial x} \right|}_{x=L}}=-\dfrac{2{{c}_{\rm eq}}}{L}\sum\limits_{n=0}^{\infty}\, {{\rm e}^{-\frac{{{\left( 2n+1 \right)}^{2}}{{\mathsf{π} }^{2}}}{4{{L}^{2}}}\frac{\tau{{D}_{\rm eff}} }{\phi }t}} $ | (8) |
对式(8)进行积分求解,得到扩散过程中压力与时间的关系
| $ p\left( {t} \right)-{{p}_{\rm eq}}=\dfrac{8{{c}_{\rm eq}}{{Z}_{\rm g}}{\rm R}T{{V}_{\rm l}}}{{{\mathsf{π} }^{2}}{{V}_{\rm g}}}\sum\limits_{n=0}^{\infty}\, \dfrac{{{{\rm e}}^{-\frac{{{(2n+1)}^{2}}{{\mathsf{π} }^{2}}}{4{{L}^{2}}}\frac{\tau{{D}_{\rm eff}} }{\phi }t}}}{{{(2n+1)}^{2}}} $ | (9) |
式中:
采用Zhang[11]提出的对潜伏期修正方法,将式(9)写成无穷级数形式,考虑到更高级项级数对扩散过程影响逐渐减小,选取无穷级数前两项,可得
| $ p\left( { t} \right)={{m}_{1}}{{\rm e}^{-\frac{t}{{{k}_{1}}}}}+{{m}_{2}}{\rm e}^{ -\frac{t}{{{k}_{2}}} }+{{p}_{\rm eq}} $ | (10) |
式中:
根据式(10)对扩散实验记录的压力—时间数据进行拟合,即可得到超临界CO
| $ {{D}_{\rm eff}}=\dfrac{4{{L}^{2}}\phi }{{{k}_{\rm L}}\tau {{\mathsf{π} }^{2}}} $ | (11) |
式中:
根据式(10)对扩散实验压力-时间数据进行拟合,不同实验条件下的拟合计算结果如表 2所示。由表 2可见,不同实验条件下的数值拟合相关系数
| 表2 扩散系数测定结果(50.0 ℃) Tab. 2 Experimental results of diffusion coefficient(50.0 ℃) |
表 3比较了本文和文献测得的CO
| 表3 文献中扩散系数与本文所测结果对比 Tab. 3 Comparison of diffusion coefficient between the literature and this paper |
图 2为初始压力与扩散系数的关系图。当实验温度为50.0 ℃,在实验设定的压力范围内,CO
 |
| 图2 扩散系数与初始压力关系 Fig. 2 Relationship between diffusion coefficient and pressure |
当压力达到临界点以上,随着压力的升高,超临界CO
从扩散系数与基质渗透率关系曲线(图 3a)可见,超临界CO
 |
| 图3 基质渗透率与扩散系数关系与渗透率临界值的确定 Fig. 3 Relationship between diffusion coefficient and permeability and determination of permeability threshold |
通过图 3b中所示的线性拟合方法,确定了渗透率临界值为10.55 mD,即当基质渗透率大于10.55 mD,渗透率对超临界CO
对基质孔隙度和迂曲度与超临界CO
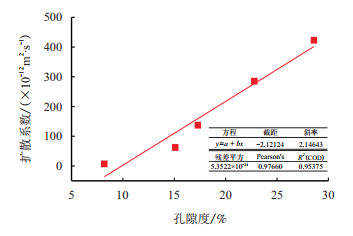 |
| 图4 孔隙度与扩散系数关系图 Fig. 4 Relationship between porosity and diffusion coefficient |
 |
| 图5 多孔介质中的扩散类型 Fig. 5 Diffusion types in porous media |
基质孔隙度越低,超临界CO
扩散系数与迂曲度关系图如图 6所示。
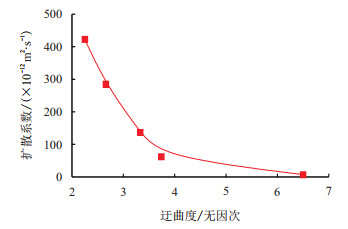 |
| 图6 迂曲度与扩散系数关系图 Fig. 6 Relationship between tortuosity and diffusion coefficient |
由图 6可见,基质迂曲度增大,超临界CO
将扩散数学模型的解无因次化,得到无因次浓度的表达式(12)
| $ \left \{ \begin{array}{l} C\left( x_{\rm D}, t_{\rm D} \right)=1-\dfrac{4}{\mathsf{π} }\sum\limits_{n=0}^{\infty}\dfrac{{{(-1)}^{n}}}{2n+1}{{{\rm e}}^{-\frac{{{(2n+1)}^{2}}{{\mathsf{π} }^{2}}}{4}\frac{\tau }{\phi }t_{\rm D}}} \cdot {\cos}\dfrac{\left( 2n+1 \right)\mathsf{π} x_{\rm D}}{2} \\ x_{\rm D} = x/L \\ t_{\rm D}=Dt/L^2 \end{array} \right . $ | (12) |
式中:
运用式(12)可进行反演预测超临界CO
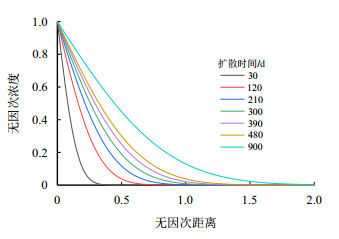
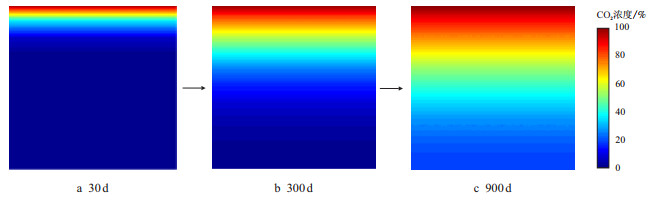
图 7为不同扩散时间内超临界CO
 |
|
图7
不同扩散时间超临界CO |
图 8为扩散前缘随扩散时间变化规律变化曲线,图 9为超临界CO
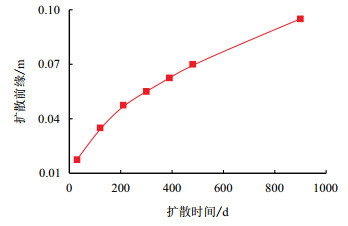 |
| 图8 扩散前缘随扩散时间变化规律 Fig. 8 Change of diffusion front with time |
 |
|
图9
超临界CO |
从图 8可以看到,随着扩散时间增加,扩散前缘位置越来越远,但曲线斜率呈现先大后小规律,说明整个扩散过程中扩散系数可能并不是常数,而是随着扩散进行在逐渐减小。
图 10为扩散120 d内,不同扩散系数所对应的超临界CO
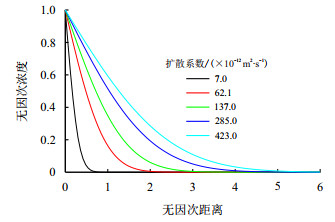 |
| 图10 不同扩散系数对应的扩散前缘(120 d) Fig. 10 Diffusion front at different diffusion coefficients(120 d) |
由图 10可见,在一定的扩散时间内,扩散系数越大,扩散前缘位置越远。同时,由于图中不同扩散系数对应于不同的基质渗透率,因此基质渗透率越大,对应的扩散前缘越远。
图 11为基质渗透率与扩散前缘关系图。
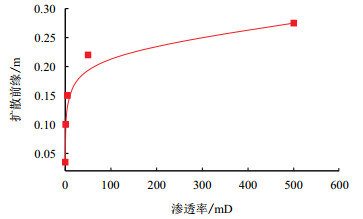 |
| 图11 基质渗透率与扩散前缘关系 Fig. 11 Diffusion front with different permeability |
由图 11可见,较低渗透率范围内扩散前缘对渗透率变化较敏感,说明基质渗透率越低对扩散的影响程度越大,随着渗透率增加,影响程度将降低。基质渗透率与前缘的关系类似于基质渗透率与扩散系数的关系,故扩散系数与扩散前缘呈线性关系。
3 结论(1) 建立的基质-裂缝模型,可以准确测定超临界CO
(2) 随着初始压力的升高,超临界CO
(3) 随着基质渗透率的增大,超临界CO
(4) 基质孔隙度的降低以及迂曲度的增大,将导致超临界CO
(5) 对于致密储层,由于CO
| [1] |
贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129-136. JIA Chengzao, ZHENG Min, ZHANG Yongfeng. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012, 39(2): 129-136. |
| [2] |
ZHANG Xiang, WEI Bing, SHANG Jing, et al. Alterations of geochemical properties of a tight sandstone reservoir caused by supercritical CO2-brine-rock interactions in CO2-EOR and geosequestration[J]. Journal of CO2 Utilization, 2018, 28: 408-418. doi: 10.1016/j.jcou.2018.11.002 |
| [3] |
魏海峰, 凡哲元, 袁向春. 致密油藏开发技术研究进展[J]. 油气地质与采收率, 2013, 20(2): 62-66. WEI Haifeng, FAN Zheyuan, YUAN Xiangchun. Research progress on tight reservoir development technology[J]. Oil and Gas Geology and Recovery, 2013, 20(2): 62-66. doi: 10.3969/j.issn.1009-9603.2013.02.016 |
| [4] |
朱维耀, 岳明, 刘昀枫, 等. 中国致密油藏开发理论研究进展[J]. 工程科学学报, 2019, 41(9): 1103-1104. ZHU Weiyao, YUE Ming, LIU Yunfeng, et al. Research progress of tight reservoir development theory in China[J]. Chinese Journal of Engineering Science, 2019, 41(9): 1103-1104. doi: 10.13374/j.issn2095-9389.2019.09.001 |
| [5] |
BALASUBRAMANIAN S, CHEN P, BOSE S, et al. Recent advances in enhanced oil recovery technologies for unconventional oil reservoirs[C]. OTC 28973-MS, 2018. doi: 10.4043/28973-MS
|
| [6] |
ZHANG Y, DI Y, YU W, et al. A comprehensive model for investigation of carbon dioxide enhanced oil recovery with nanopore confinement in the Bakken tight oil reservoir[C]. SPE 187211-PA, 2018. doi: 10.2118/187211-PA
|
| [7] |
杨俊兰, 马一太, 曾宪阳, 等. 超临界压力下CO2流体的性质研究[J]. 流体机械, 2008, 36(1): 53-57. YANG Junlan, MA Yitai, ZENG Xianyang, et al. Study on properties of CO2 fluid at supercritical pressure[J]. Fluid Machinery, 2008, 36(1): 53-57. doi: 10.3969/j.issn.1005-0329.2008.01.014 |
| [8] |
魏兵, 宋涛, 赵金洲, 等. 溶解气回注提高致密油藏采收率效果及敏感性[J]. 西南石油大学学报(自然科学版), 2019, 41(5): 85-95. WEI Bing, SONG Tao, ZHAO Jinzhou, et al. Improving the recovery efficiency and sensitivity of tight oil reservoirs by dissolved gas reinjection[J]. Journal of Southwest Petroleum University (Natural Science Edition), 2019, 41(5): 85-95. doi: 10.11885/j.issn.1674-5086.2019.07.06.01 |
| [9] |
杜林, 刘伟, 陈星杙, 等. CO2在原油中扩散系数测定方法的研究进展[J]. 油田化学, 2019, 36(2): 372-380. DU Lin, LIU Wei, CHEN Xingyi, et al. Progress in the determination of CO2 diffusivity in crude oil[J]. Oilfield Chemistry, 2019, 36(2): 372-380. doi: 10.19346/j.cnki.1000-4092.2019.02.034 |
| [10] |
RIAZI M R. A new method for experimental measurement of diffusion coefficients in reservoir fluids[J]. Journal of Petroleum Science & Engineering, 1996, 14(3-4): 235-250. doi: 10.1016/0920-4105(95)00035-6 |
| [11] |
ZHANG Y P, HYNDMAN C L, MAINI B B, et al. Measurement of gas diffusivity in heavy oils[J]. Journal of Petroleum Science and Engineering, 2000, 25(1-2): 37-47. doi: 10.1016/S0920-4105(99)00031-5 |
| [12] |
张彪.高温高压下二氧化碳在饱和油多孔介质中的扩散系数研究[D].长沙: 湖南大学, 2016. ZHANG Biao. Diffusion coefficient of carbon dioxide in oil-saturated porous media at high temperature and pressure[D]. Changsha: Hunan University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10532-1016253833.htm |
| [13] |
LI Songyan, LI Zhaomin, DONG Quanwei. Diffusion coefficients of supercritical CO2 in oil-saturated cores under low permeability reservoir conditions[J]. Journal of CO2 Utilization, 2016, 14: 47-60. doi: 10.1016/j.jcou.2016.02.002 |
| [14] |
LI Songyan, QIAO Chenyu, ZHANG Chao, et al. Determination of diffusion coefficients of supercritical CO2 under tight oil reservoir conditions with pressure-decay method[J]. Journal of CO2 Utilization, 2018, 24: 430-443. doi: 10.1016/j.jcou.2018.02.002 |
| [15] |
RENNER T A. Measurement and correlation of diffusion coefficients for CO2 and rich-gas applications[C]. SPE 15391-PA, 1988. doi: 10.2118/15391-PA https://www.researchgate.net/publication/239436024_Measurement_and_Correlation_of_Diffusion_Coefficients_for_CO2_and_Rich-Gas_Applications
|
| [16] |
YU Boming. Fractal character for tortuous streamtubes in porous media[J]. Chinese Physics Letters, 2005, 22(1): 158-160. doi: 10.1088/0256-307X/22/1/045 |
| [17] |
THARANIVASAN A K, YANG Chaodong, GU Yongan, et al. Measurements of molecular diffusion coefficients of carbon dioxide, methane, and propane in heavy oil under reservoir conditions[J]. Energy Fuels, 2006, 20(6): 2509-2517. doi: 10.1021/ef060080d |
| [18] |
WANG L S, LANG Z X, GUO T M. Measurement and correlation of the diffusion coefficients of carbon dioxide in liquid hydrocarbons under elevated pressures[J]. Fluid Phase Equilibria, 1996, 117(1-2): 364-372. doi: 10.1016/0378-3812(95)02973-7 |
| [19] |
王欢, 李正山, 洪荷芳. 超临界流体的应用及发展趋势[J]. 环境技术, 2003, 21(5): 8-10. WANG Huan, LI Zhengshan, HONG Hefang. Application and development trend of supercritical fluid[J]. Environmental Technology, 2003, 21(5): 8-10. doi: 10.3969/j.issn.1004-7204.2003.05.003 |
| [20] |
王爱荣, 王跃, 唱桂凤. Maxwell Stefan方程在多孔结构内传质方面的应用[J]. 山东理工大学学报(自然科学版), 2004, 18(3): 100-105. WANG Airong, WANG Yue, CHANG Guifeng. MaxwellStefan equation to mass transfer in porous structure[J]. Journal of Shandong University of Technology (Natural Science Edition), 2004, 18(3): 100-105. doi: 10.3969/j.issn.1672-6197.2004.03.024 |
 2020, Vol. 42
2020, Vol. 42


