随着井深的增加地层压力显著增加,相应关井压力也将增加,5 000 m深井的关井压力高达50 MPa,而异常高压井关井压力达到70 MPa,甚至有的固井设计要求高于100 MPa[1]。高压环境下,套管腐蚀缺陷大幅降低了连接螺纹承载能力,导致高压井的安全生产隐患严重。
针对套管腐蚀缺陷后的强度评价方法,许多专家学者对此开展了大量研究工作。Coulson等提出了套管双腐蚀缺陷沿轴向相互作用影响规律,为研究多腐蚀缺陷下的强度行为奠定了基础[2]。O'Grady等得出了腐蚀缺陷间的间距沿轴向或环向变化时的影响规律,获得腐蚀缺陷之间不相互干涉的极限距离,为腐蚀后多缺陷强度评判提供了依据[3]。之后,有学者专家对相邻腐蚀问题做了研究[4-5]。Sun Kai等研究了球形缺陷应力集中系统数学模型,为具有球形腐蚀缺陷的套管强度评价提供了依据[6]。随后,许多专家学者针对不同腐蚀工况下剩余强度问题进行了更为精确评估方法研究。石晓兵等建立了CO2点蚀模型,基于弹塑性有限元分析理论及方法,研究了点蚀套管的抗外压强度、抗内压强度、极限承载强度的变化[7]。慕立俊等通过理论推导的方式分析了套管壁厚均匀减薄对承载强度的影响,得出了中国几大套管生产厂家套管承载强度变化规律[8]。李文飞等对套管腐蚀后的形貌进行了分类,并针对不同形貌下的套管腐蚀强度进行评价,建立了腐蚀量与强度影响的变化规律[9]。许志倩等建立了全井套管柱腐蚀后的剩余强度时变性分析系统,分析获得套管承载强度影响权重由大到小依次为:点状腐蚀、均匀腐蚀、缝隙腐蚀[10]。张智等从均匀腐蚀和点蚀等角度出发,分析了温度、内压对套管等效应力的影响,研究了套管剩余强度随腐蚀深度增加的变化规律,以及点蚀开口直径对套管剩余强度的影响[11]。
套管接头螺纹由于其结构特点,其连接螺纹牙处是油套管的最薄弱环节,承载能力不足管体强度的70%[12],调查发现,80%以上的失效事故发生在套管接头的螺纹连接处[13]。许多专家学者对套管螺纹牙承载强度性能进行了大量分析研究工作。龚伟安分析了套管密封性能与连接强度间关系[14]。Wang Li等通过实验的方式研究了API圆螺纹套管连接处应力场分布规律[15]。李黔等研究了轴向载荷对套管螺纹连接强度影响规律[16]。高连新等提出了优化套管螺纹承载强度的措施[17]。袁光杰等分析了API偏梯形套管螺纹在多种载荷作用下的应力场分布规律[18]。石晓兵等分析了井筒内高压气流对套管接头螺纹密封性能的影响[1]。李挺前等利用商用有限元软件分析了套管螺纹应力在不同载荷类型下的变化规律[19]。刘金坡等以API圆螺纹为研究对象分析了井下作业载荷对套管连接强度的影响[20]。唐明应用有限元分析软件研究了膨胀套管接头螺纹受力变化规律[21]。然而,针对腐蚀后套管接头螺纹的连接强度影响,却鲜有报道,而套管接头一旦发生失效,不仅会影响到套管柱的密封完整性和结构完整性以及正常的钻井作业,而且有可能导致油井的报废。
因此,进一步研究套管接头腐蚀后的强度行为,对提高套管作业的安全性及套管的合理修复具有重要意义。
1 平面系统模型解及理论 1.1 平面系统简化模型解将套管的内螺纹与外螺纹简化为一个胶结的薄壁圆筒,对其施加地层应力载荷和内压载荷,可将其简化为平面系统模型[22]。假定地层、水泥环、套管均为各向同性弹性材料,载荷施加时系统内部各层接触界面变形连续。设a,b,c,R分别是套管内壁半径、套管外壁半径、水泥环外壁半径、地层内壁半径,简化的平面系统模型如图 1所示。
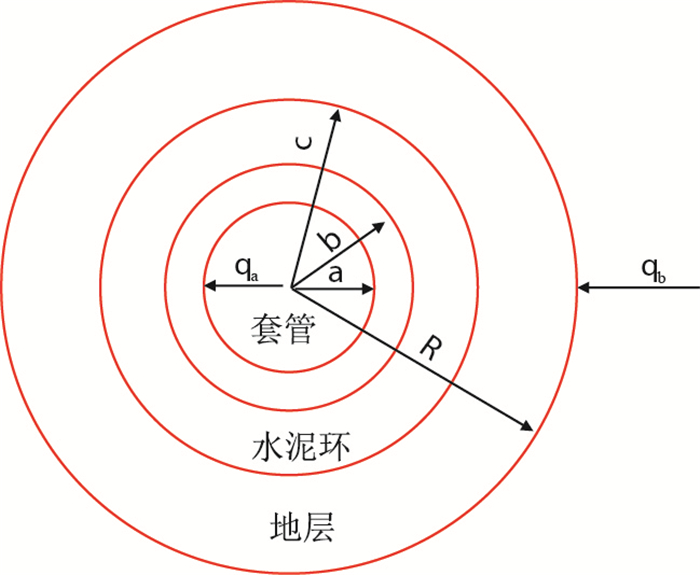 |
| 图1 平面系统简化模型 Fig. 1 Simplified model of graphic system |
对于平面系统模型,可计算得到任意位置的应力和位移
| $ \left\{ \begin{array}{l} {{σ }_{ρ }}=\dfrac{A}{{{ρ }^{2}}}+2C \\ {{σ }_{φ }}=-\dfrac{A}{{{ρ }^{2}}}+2C \\ {{μ }_{ρ }}=\dfrac{1-{{μ }^{2}}}{E}\left[ -\left( 1+\dfrac{μ }{1-μ } \right)\dfrac{A}{ρ }+2\left( 1-\dfrac{μ }{1-μ } \right)Cρ \right]+I\cos φ +K\sin φ \\ \end{array} \right. $ | (1) |
式中:
σρ-任一点的径向应力分量,Pa;
σφ-任一点的环向应力分量,Pa;
μρ-任一点的径向位移分量,m;
A,C,I,K-关于材料属性的常数,无因次;
μ-泊松比,无因次;
E-系统材料弹性模量,Pa;
ρ -任一点的半径,m;
φ-任意一点的环向夹角,(°)。
套管、水泥环、地层的应力分量表达式分别为
| $ \left\{ \begin{array}{l} {{σ }_{ρ {\rm{t}}}}=\dfrac{A_{\rm{t}}}{{{ρ }^{2}}}+2C_{\rm{t}} \\ {{σ }_{φ {\rm{t}}}}=-\dfrac{A_{\rm{t}}}{{{ρ }^{2}}}+2C_{\rm{t}} \\ \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} {{σ }_{ρ {\rm{s}}}}=\dfrac{{{A_{\rm{s}}}}}{{{ρ }^{2}}}+2{C_{\rm{s}}} \\ {{σ }_{φ {\rm{s}}}}=-\dfrac{{{A_{\rm{s}}}}}{{{ρ }^{2}}}+2{C_{\rm{s}}} \\ \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} {{σ }_{ρ {\rm{d}}}}=\dfrac{{{A_{\rm{d}}}}}{{{ρ }^{2}}}+2{C_{\rm{d}}} \\ {{σ }_{φ {\rm{d}}}}=-\dfrac{{{A_{\rm{d}}}}}{{{ρ }^{2}}}+2{C_{\rm{d}}} \\ \end{array} \right. $ | (4) |
式中:
σρt-套管的径向应力分量,Pa;
σφt-套管的环向应力分量,Pa;
σρs-水泥环的径向应力分量,Pa;
σφs-水泥环的环向应力分量,Pa;
σρd-地层的径向应力分量,Pa;
σφd-地层的环向应力分量,Pa;
At,Ct-套管材料属性常数;
As,Cs-水泥环材料属性常数;
Ad,Cd-地层材料属性常数。
求解At,As,Ad,Ct,Cs,Cd的6个边界条件
| $ {{\left( {{σ }_{ρ {\rm{t}}}} \right)}_{ρ =a}}={{q}_{\rm{a}}} $ | (5) |
| $ {{\left( {{σ }_{ρ {\rm{t}}}} \right)}_{ρ =b}}={{\left( {{σ }_{ρ {\rm{s}}}} \right)}_{ρ =b}} $ | (6) |
| $ {{\left( {{σ }_{ρ {\rm{s}}}} \right)}_{ρ =c}}={{\left( {{σ }_{ρ {\rm{d}}}} \right)}_{ρ =c}} $ | (7) |
| $ {{\left( {{σ }_{ρ {\rm{d}}}} \right)}_{ρ =+∈fty }}={{q}_{\rm{b}}} $ | (8) |
| $ {{\left( {{μ }_{ρ {\rm{t}}}} \right)}_{ρ =b}}={{\left( {{μ }_{ρ {\rm{s}}}} \right)}_{ρ =b}} $ | (9) |
| $ {{\left( {{μ }_{ρ {\rm{s}}}} \right)}_{ρ =c}}={{\left( {{μ }_{ρ {\rm{d}}}} \right)}_{ρ =c}} $ | (10) |
式中:
qa-地层应力,Pa;
qb-套管内侧压力,Pa;
μρt-套管的径向位移分量,m;
μρs-水泥环的径向位移分量,m;
μρd-地层的径向位移分量,m。
将式(9)、式(10)代入式(1)中整理,可得
| $ \left\{ \begin{array}{l} \dfrac{1+{{μ}_{\rm{t}}}}{{{E}_{\rm{t}}}}\left[ 2\left( 1-2{{μ }_{\rm{t}}} \right)C_{\rm{t}}b-\dfrac{A_{\rm{t}}}{b} \right]+{{I}_{\rm{t}}}\cos φ +{{K}_{\rm{t}}}\sin φ =\dfrac{1+{{μ }_{\rm{s}}}}{{{E}_{\rm{s}}}}\left[ 2\left( 1-2{{μ }_{\rm{s}}} \right){C_{\rm{s}}}b-\dfrac{{{A_{\rm{s}}}}}{b} \right]+ \\ {{I}_{\rm{s}}}\cos φ +{{K}_{\rm{s}}}\sin φ \\ \dfrac{1+{{μ }_{\rm{s}}}}{{{E}_{\rm{s}}}}\left[ 2\left( 1-2{{μ }_{\rm{s}}} \right){C_{\rm{s}}}c-\dfrac{{{A_{\rm{s}}}}}{c} \right]+{{I}_{\rm{s}}}\cos φ +{{K}_{\rm{s}}}\sin φ =\dfrac{1+{{μ }_{\rm{d}}}}{{{E}_{\rm{d}}}}\left[ 2\left( 1-2{{μ }_{\rm{d}}} \right){C_{\rm{d}}}c-\dfrac{{{A_{\rm{d}}}}}{c} \right] + \\ {{I}_{\rm{d}}}\cos φ +{{K}_{\rm{d}}}\sin φ \\ \end{array} \right. $ | (11) |
式中:
下标:t-套管;s-水泥环;d-地层。
由于该方程在接触面上任意一点都应成立,即在φ取任何值时都应成立,则方程自由项必须相等,即:It cos φ +Kt sin φ =Is cos φ +Ks sin φ;同理可得:Is cos φ +Ks sin φ =Id cos φ +{Kd sin φ。
令
| $ \left\{ \begin{array}{l} n=\dfrac{2\left( 1-2{{μ }_{\rm{s}}} \right){C_{\rm{s}}}b-\dfrac{{{A_{\rm{s}}}}}{b}}{2\left( 1-2{{μ }_{\rm{t}}} \right)C_{\rm{t}}b-\dfrac{A_{\rm{t}}}{b}} \\ {n}{'}=\dfrac{2\left( 1-2{{μ }_{\rm{d}}} \right){C_{\rm{d}}}c-\dfrac{{{A_{\rm{d}}}}}{c}}{2\left( 1-2{{μ }_{\rm{s}}} \right){C_{\rm{s}}}c-\dfrac{{{A_{\rm{s}}}}}{c}} \\ \end{array} \right. $ | (12) |
联立其他4个边界条件,即可求出At,As,Ad,Ct,Cs,Cd,进而得到套管-水泥环-地层平面系统上任意一点的应力分量σρ和σφ,根据等效应力计算公式
套管的失效形式以局部塑性失效为主,即当腐蚀缺陷区内套管所受的等效(Von Mises)应力达到套管的屈服极限后即发生失效[23]。故采用米塞斯屈服准则来评价套管屈服与否,表达式为
| $ {{σ }_{\rm{S}}} - {{σ }_{\rm{R}}} = {{σ }_{\rm{S}}}-\sqrt{\dfrac{1}{2}\left[ {{\left( {{σ } _{1}} - {{σ }_{2}} \right) }^{2}} + {{\left( {{σ }_{2}} - {{σ }_{3}} \right)}^{2}} + {{\left( {{σ }_{3}} - {{σ }_{1}} \right)}^{2}} \right]} $ | (13) |
式中:
σ1,σ2,σ3-第一、二、三主应力,Pa;
σS-服役套管屈服强度,Pa;
σR-服役套管最大等效应力,Pa。
若计算σS-σR >0,套管处于弹性状态,否则套管处于塑性状态。
2 有限元模型建立以API ϕ177.8 mm×12.65 mm P110钢级套管为研究对象,选用长圆螺纹[24],其材料屈服强度为758 MPa。根据套管接头的结构和受力特点,在有限元建模时引入以下简化和假设:(1)忽略螺旋升角的影响;(2)为消除力学模型中边界效应带来的影响,模型总长度取2 m;(3)对套管-水泥环-地层系统模型仅施加内压qa和地层应力qb。为提高计算精度,套管螺纹牙处网格细化,网格划分如图 2所示。
 |
| 图2 套管螺纹牙网格划分 Fig. 2 Casing thread mesh |
取水泥环外半径c=108.4 mm,内压qa取15~MPa,地层应力qb取40 MPa,套管、水泥环、地层材料参数如表 1所示。
| 表1 材料参数 Tab. 1 Material parameters |
根据表 1中的材料参数,可计算得n=0.081 88,n'=1.943 68。通过理论计算及有限元仿真两种方式,得到各接触的计算应力和模拟应力值,其结果如表 2所示。可以看出,运用本文推导的套管-水泥环-地层平面应力计算公式得到的边界应力值与仿真计算结果间的误差最大为3.084 7%,证明了两者计算结果的可靠性。
| 表2 各接触的计算应力值和模拟应力值比较 Tab. 2 Comparison of the computation results and simulation results |
为研究不同形状腐蚀缺陷对套管螺纹牙承载能力的影响,建立3种腐蚀形态:均匀腐蚀、沟槽型腐蚀、点蚀。均匀腐蚀,即整个表面均匀发生腐蚀,壁厚均匀减薄,其几何模型如图 3a所示;局部腐蚀主要包含局部减薄型腐蚀和沟槽型腐蚀,此处选用沟槽型腐蚀缺陷,采用长40 mm、宽与腐蚀深度为h的几何矩形来模拟,其几何模型如图 3b所示;点蚀主要是由CO2引起的套管表面点状(坑状)腐蚀缺陷,采用半径为13 mm的圆,按照腐蚀深度h切削形成规则的浅球型来模拟腐蚀坑,其几何模型如图 3c所示。
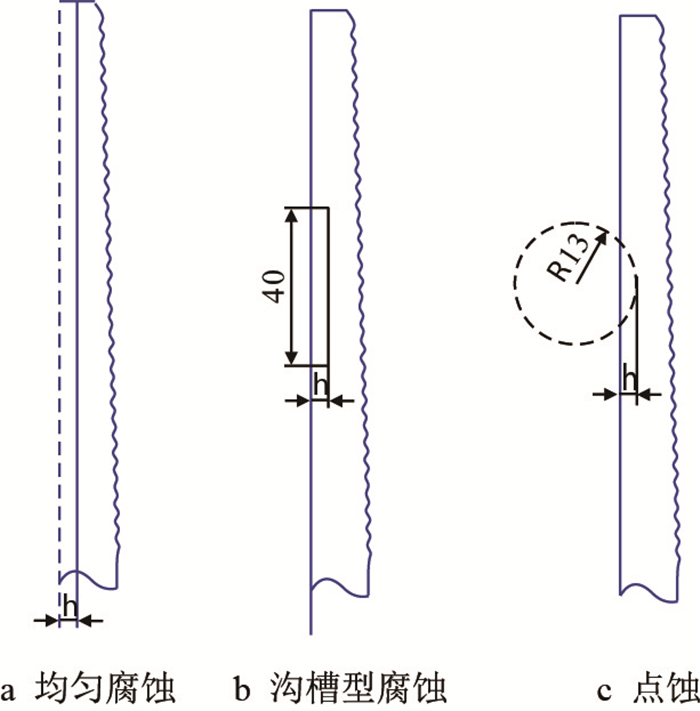 |
| 图3 腐蚀缺陷几何模型 Fig. 3 Geometric model of the corrosion defects |
沟槽型腐蚀和点蚀发生的位置多变,为精确分析腐蚀缺陷对套管螺纹牙承载能力的影响,需对腐蚀缺陷的不同轴向位置分别讨论研究。将螺纹啮合区域的上顶点、中心点、下顶点设为3个缺陷区域的几何中心点,按照该几何中心点上下延伸的区域为缺陷区域,分别为上段缺陷区域、中段缺陷区域、下段缺陷区域。腐蚀缺陷轴向相对位置设置如图 4所示。
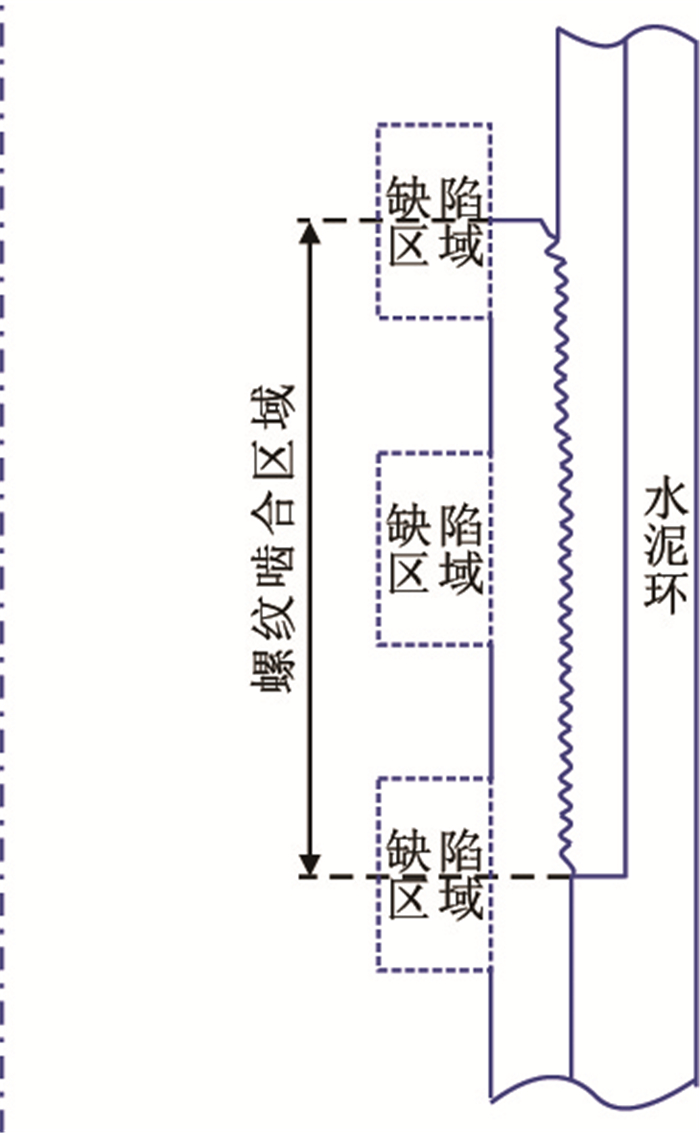 |
| 图4 腐蚀缺陷轴向相对位置 Fig. 4 Axial position of the corrosion defects |
针对低压气井和高压井特点作4种工况假设:(1)内压15 MPa,外压(地层压力)40 MPa;(2)内压30 MPa,外压50 MPa;(3)内压70 MPa,外压50 MPa;(4)内压100 MPa,外压50 MPa。得到4种载荷下不含腐蚀缺陷套管螺纹牙应力分布(图 5)。
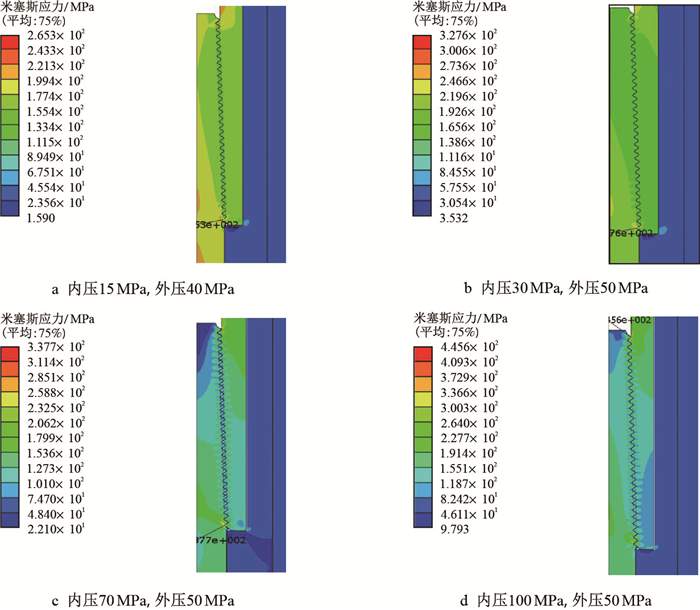 |
| 图5 4种载荷下不含腐蚀缺陷套管螺纹牙应力分布图 Fig. 5 Integrity casing thread stress cloud under the four kinds of load |
将啮合的内外螺纹牙作为一个“大螺纹牙”,且内外螺纹牙应力较大的值作为“大螺纹牙”的应力值,并对“大螺纹牙”进行编号。编号按照从公螺纹的大端到小端依次排序。由图 5可知,4种载荷下套管螺纹牙应力分布呈现两端大、中间低状态,最大等效应力值出现在1号螺纹牙处或者末尾31号螺纹牙处。腐蚀缺陷越接近首端1号螺纹牙和末尾31号螺纹牙,套管最大等效应力值越大。
4.2 均匀腐蚀缺陷计算不同壁厚下套管连接螺纹牙最大等效应力。图 6为不同均匀腐蚀深度下套管连接螺纹在内压与地层压力共同作用下的最大等效应力变化曲线图。
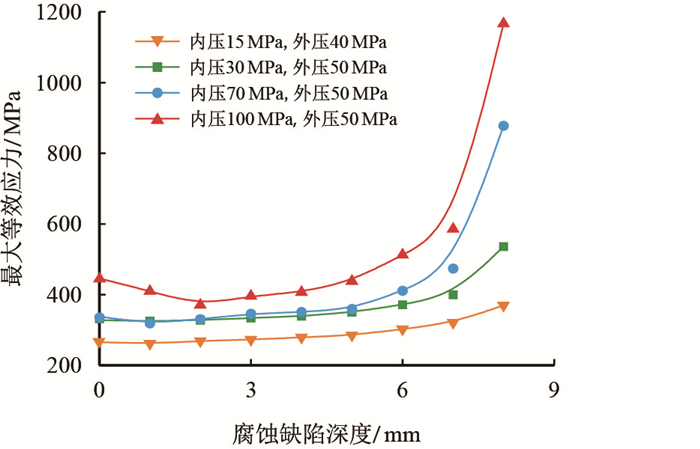 |
| 图6 均匀腐蚀缺陷 Fig. 6 Homogeneous corrosion |
由图 6可知:4种工况下,随着腐蚀缺陷深度的增加,套管螺纹牙最大等效应力都呈现增大趋势。当腐蚀缺陷深度达到7 mm时,套管螺纹牙最大等效应力突然上升,且气井的压力越大,该现象越明显。在内压100 MPa,外压50 MPa的高压井中,当套管屈服的临界腐蚀缺陷深度为7 mm及以上时,套管螺纹牙最大等效应力值达到甚至超过了套管螺纹屈服强度,此时套管处于极度危险状态,需要进行套管修复或更换。
4.3 沟槽型腐蚀缺陷沟槽型腐蚀腐蚀面积相对较小,可能发生在套管内壁任意位置,为方便分析沟槽型腐蚀缺陷对套管螺纹牙承载能力的影响,现按照图 4划分的上-中-下三段腐蚀区域进行仿真计算,得到4种工况下套管螺纹牙最大等效应力随腐蚀缺陷深度增加而变化的应力曲线图。
图 7~图 9为4种工况下套管螺纹牙最大等效应力随沟槽型腐蚀缺陷深度增加而变化的应力曲线图。由图 7中可知,缺陷深度小于7 mm时,4种工况下上段沟槽型腐蚀缺陷套管螺纹牙最大等效应力随着腐蚀缺陷深度的增加呈现平稳趋势。当腐蚀缺陷深度在7 mm及以上时套管螺纹牙最大等效应力陡然增加,且气井的压力越大,该现象越明显,套管失效的可能性越高需根据具体井场工况进行判断。由图 8可知,低压气井中中段沟槽型腐蚀缺陷套管螺纹牙最大等效应力随腐蚀深度增加而无明显变化,在高压井中呈现先微降后平稳增加的趋势,但均未达到屈服强度,套管较为安全。由图 9可知,4种工况下下段沟槽型腐蚀缺陷套管螺纹牙最大等效应力值随着腐蚀缺陷深度增加都呈现先稳定后增加趋势。
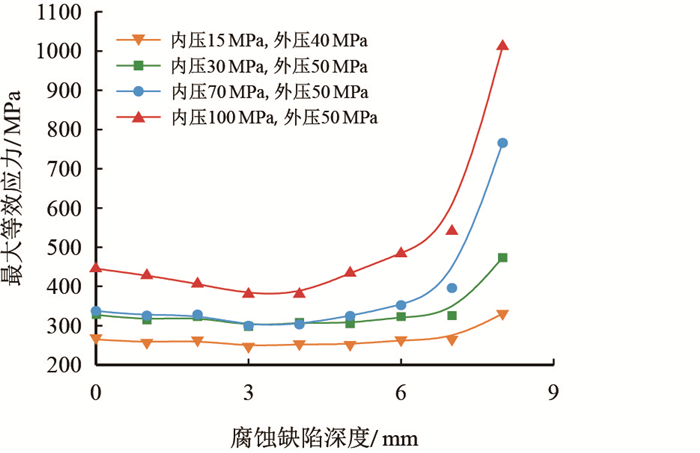 |
| 图7 上段沟槽型腐蚀缺陷 Fig. 7 Groove corrosion in upper section |
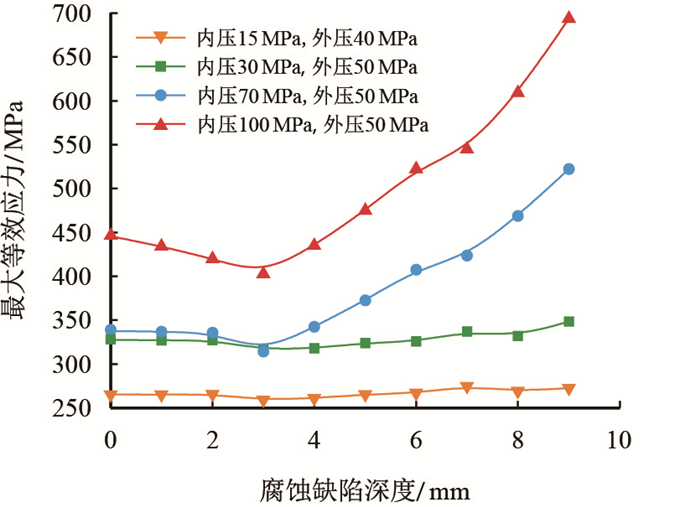 |
| 图8 中段沟槽型腐蚀缺陷 Fig. 8 Groove corrosion in middle section |
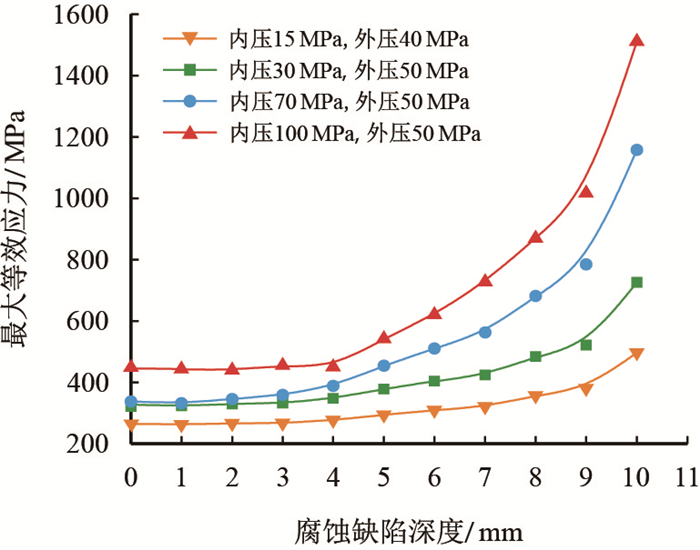 |
| 图9 下段沟槽型腐蚀缺陷 Fig. 9 Groove corrosion in bottom section |
通过以上计算分析发现:(1)相同腐蚀条件下,气井压力越高,套管螺纹牙的最大等效应力值越大;(2)中段沟槽型腐蚀缺陷对套管螺纹牙的影响较小。
4.4 点蚀图 10~图 12为4种工况下套管螺纹牙最大等效应力随点蚀深度增加而变化的应力曲线图。
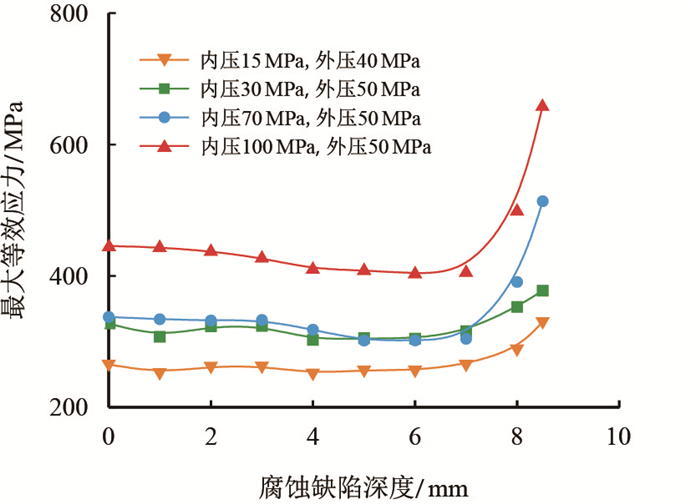 |
| 图10 上段点蚀 Fig. 10 Point corrosion in upper section |
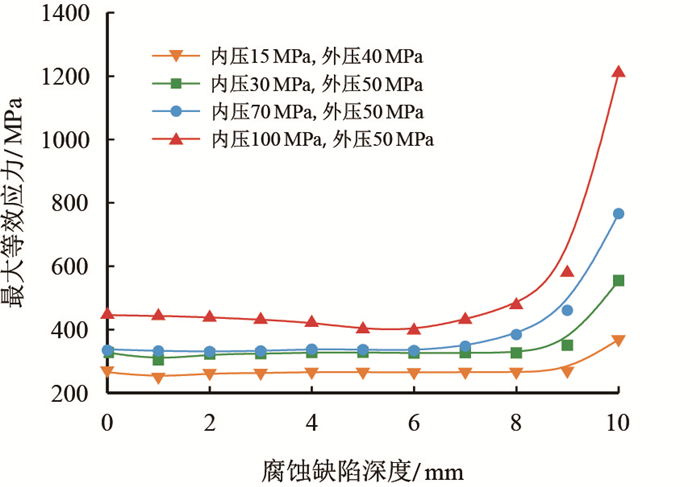 |
| 图11 中段点蚀 Fig. 11 Point corrosion in middle section |
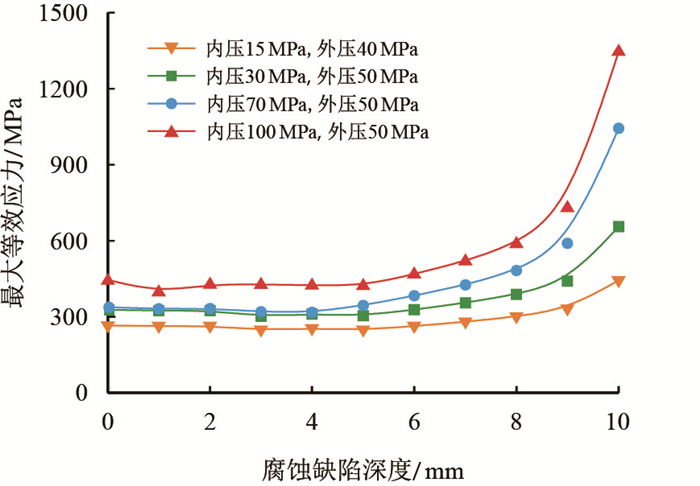 |
| 图12 下段点蚀 Fig. 12 Point corrosion in bottom section |
由图 10可知,当点蚀位于螺纹上段时,套管螺纹牙最大等效应力随腐蚀缺陷深度的增加无明显变化,腐蚀缺陷深度达到7 mm时,最大等效应力有小幅度增加,但均未达到屈服强度,套管安全。由图 11可知,当点蚀位于螺纹中段,且腐蚀深度小于10 mm时,套管螺纹牙最大等效应力无明显变化,当腐蚀深度达到10 mm时,两种高压井工况下套管发生了屈服。由图 12可知,当点蚀位于螺纹下段时,套管螺纹牙最大等效应力随着腐蚀缺陷深度增加呈现先平稳后增加趋势。腐蚀缺陷深度在1~5 mm时,最大等效应力值无明显变化,此后随着腐蚀深度增加呈现上升趋势。
5 结论(1) 均匀腐蚀缺陷相对于低压气井对高压井套管螺纹牙最大等效应力影响较大,最大等效应力值随着腐蚀缺陷深度的增加而增加。内压100 MPa地层应力50 MPa的高压井中,套管的临界屈服腐蚀深度为7 mm,超过7 mm套管屈服失效。
(2) 沟槽型腐蚀缺陷发生在套管螺纹啮合区域下段相对于上段、中段对套管螺纹牙最大等效应力影响显著。内压100 MPa地层应力50 MPa高压井中,套管的临界屈服腐蚀缺陷深度为6 mm。
(3) 点蚀对套管螺纹牙最大等效应力影响变化同沟槽型腐蚀缺陷相似,但影响要弱于沟槽型腐蚀缺陷的影响,内压100 MPa地层应力50 MPa高压井中,下段点蚀缺陷套管的临界屈服腐蚀缺陷深度为8 mm。
| [1] |
石晓兵, 陈平, 聂荣国, 等. 高压对气井套管接头螺纹接触应力的影响研究[J]. 石油机械, 2006, 34(6): 32-34. SHI Xiaobing, CHEN Ping, NIE Rongguo, et al. The influence of high pressure on thread contact stress of casing joints in gas wells[J]. China Petroleum Machinery, 2006, 34(6): 32-34. doi: 10.3969/j.issn.1001-4578.2006.06.010 |
| [2] |
COULSON K, WORTHINGAM R. New guidelines promise more accurate damage assessment[J]. Oil and Gas Journal, 1990, 88(16): 41-45. |
| [3] |
O'GRADY T, HISEY D, KIEFNER J. A systematic method for the evaluation corroded pipelines[J]. Pipelines Engineering, ASME, 1992, 46: 27-35. |
| [4] |
赵新伟, 罗金恒, 路民旭. 含腐蚀缺陷管道剩余强度的有限元法分析[J]. 油气储运, 2001, 20(3): 18-21. ZHAO Xinwei, LUO Jinheng, LU Minxu. FEM analysis on the effect of corroded flaw interaction on remaining storage of line pipe[J]. Oil & Gas Storage and Transportation, 2001, 20(3): 18-21. doi: 10.3969/j.issn.1000-8241-D.2001.03.005 |
| [5] |
董事尔, 何东升, 张鹏, 等. 双点腐蚀管道的弹塑性有限元分析[J]. 机械, 2005, 32(9): 20-22, 56. DONG Shier, HE Dongsheng, ZHANG Peng, et al. The elastic and plastic finite element analysis of double points corrosive pipe[J]. Machinery, 2005, 32(9): 20-22, 56. doi: 10.3969/j.issn.1006-0316.2005.09.008 |
| [6] |
SUN Kai, GUO Boyun, GHALAMBOR A. Casing strength degradation due to corrosion-applications to casing pressure assessment[C]. SPE 88009-MS, 2004. doi: 10.2118/88009-MS
|
| [7] |
石晓兵, 陈平, 徐进, 等. 油气井套管CO2点状腐蚀剩余强度分析[J]. 天然气工业, 2006, 26(2): 95-97. SHI Xiaobing, CHEN Ping, XU Jin, et al. Analysis on residual strength of CO2 tubercular corrosion for casings of oil/gas wells[J]. Natural Gas Industry, 2006, 26(2): 95-97. doi: 10.3321/j.issn:1000-0976.2006.02.029 |
| [8] |
慕立俊, 张军, 赵文轸, 等. 均匀腐蚀下油气井套管的强度及其寿命[J]. 石油化工腐蚀与防护, 2010, 27(4): 10-13. MU Lijun, ZHANG Jun, ZHAO Wenzhen, et al. Strength and service life of casing under uniform corrosion[J]. Corrosion & Protection in Petrochemical Industry, 2010, 27(4): 10-13. doi: 10.3969/j.issn.1007-015X.2010.06.003 |
| [9] |
李文飞, 李玄烨, 夏文安. 腐蚀套管剩余强度数值模拟分析[J]. 天然气与石油, 2013, 31(6): 70-75. LI Wenfei, LI Xuanye, XIA Wenan. Numerical simulation analysis on corroded casing residual strength[J]. Natural Gas and Oil, 2013, 31(6): 70-75. doi: 10.3969/j.issn.1006-5539.2013.06.020 |
| [10] |
许志倩, 闫相祯, 杨秀娟, 等. 不同缺陷对套管剩余强度影响分析[J]. 机械设计, 2014, 31(8): 74-78. XU Zhiqian, YAN Xiangzhen, YANG Xiujuan, et al. Different defects impact analysis on casing residual strength[J]. Journal of Machine Design, 2014, 31(8): 74-78. doi: 10.3969/j.issn.2095-509X.2014.08.018 |
| [11] |
张智, 孔维伟, 刘志伟, 等. 腐蚀缺陷套管的剩余强度研究[J]. 中国科技论文, 2016, 11(21): 2467-2472. ZHANG Zhi, KONG Weiwei, LIU Zhiwei, et al. Study on residual strength of corrosion defect casing[J]. China Sciencepaper, 2016, 11(21): 2467-2472. doi: 10.3969/j.issn.2095-2783.2016.21.013 |
| [12] |
袁光杰. API圆螺纹接头力学性能的数值仿真与实验研究[D].上海: 上海交通大学, 2004. YUAN Guangjie. Numerical simulation and experimental research on mechanical behavior of API round threaded connection[D]. Shanghai: Shanghai Jiaotong University, 2004. http://d.wanfangdata.com.cn/Thesis_Y671620.aspx |
| [13] |
马永才. 油管螺纹连接上扣状态受力分析[J]. 中国材料科技与设备, 2008(3): 80-83. MA Yongcai. The forced-summing analysis on tubing thread connection under maked-up state[J]. Chinese Materials Science Technology & Equipment, 2008(3): 80-83. |
| [14] |
龚伟安. 略论套管螺纹密封性能与联接应力的关系[J]. 石油机械, 1995, 23(6): 27-36. GONG Weian. Relation of the sealing ability of casing threads to connection stress[J]. China Petroleum Machinery, 1995, 23(6): 27-36. |
| [15] |
WANG Li, ZHANG Ruxin, ZOU Jiaxiang, et al. Experimental research of stress field distribution on API round thread casing connection[J]. Journal of University of Science and Technology Beijing (China), 2000, 22(6): 555-558. doi: 10.3321/j.issn:1001-053X.2000.06.018 |
| [16] |
李黔, 冯少波. 轴向载荷对套管螺纹连接应力的影响分析[J]. 西南石油学院学报, 2002, 24(1): 81-83. LI Qian, FENG Shaobo. Effect of axial load on casing threads connection stress[J]. Journal of Southwest Petroleum Institute, 2002, 24(1): 81-83. doi: 10.3863/j.issn.1674-5086.2002.01.025 |
| [17] |
高连新, 金烨, 张毅. 优化套管螺纹载荷分布特性的方法[J]. 机械科学与技术, 2003, 22(增): 28-30, 61. GAO Lianxin, JIN Ye, ZHANG Yi. A method for optimizing the load distribution on casing thread[J]. Mechanical Science and Technology, 2003, 22(S): 28-30, 61. |
| [18] |
袁光杰, 林元华, 姚振强, 等. API偏梯形套管螺纹连接的接触应力场研究[J]. 钢铁, 2004, 39(9): 35-38. YUAN Guangjie, LIN Yuanhua, YAO Zhenqiang, et al. Research on contact stress field of API buttress casing thread connection[J]. Iron & Steel, 2004, 39(9): 35-38. doi: 10.3321/j.issn:0449-749X.2004.09.008 |
| [19] |
李挺前, 沈建, 黄海龙, 等. 基于ANSYS的套管螺纹应力分析[J]. 广东化工, 2012, 39(4): 20. LI Tingqian, SHEN Jian, HUANG Hailong, et al. Stress analysis of threaded sleeve based on ANSYS[J]. Guangdong Chemical Industry, 2012, 39(4): 20.208, 168. doi: 10.3969/j.issn.1007-1865.2012.04.106 |
| [20] |
刘金坡, 焦永树, 龙连春.石油套管螺纹连接强度分析[C].北京: 北京力学会第20届学术年会论文集, 2014.
|
| [21] |
唐明. 等井径膨胀套管螺纹接头的应力分析[J]. 石油机械, 2015, 43(6): 11-15. TANG Ming. The stress of the thread connection of monodiameter expandable tubular[J]. China Petroleum Machinery, 2015, 43(6): 11-15. doi: 10.16082/j.cnki.issn.1001-4578.2015.06.003 |
| [22] |
唐晓鸿.水泥环缺陷对套管接头螺纹牙承载能力影响分析[D].成都: 西南石油大学, 2017. TANG Xiaohong. Analysis of influence of cement ring defects on bearing capacity of threaded joint of casing joint[D]. Chengdu: Southwest Petroleum University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10615-1017108030.htm |
| [23] |
孙濡青.热采井腐蚀套管剩余强度与剩余寿命研究[D].成都: 西南石油大学, 2014. SUN Ruqing. Study on residual strength and residual life of corroded bushing in thermal recovery well[D]. Chengdu: Southwest Petroleum University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10615-1014415679.htm |
| [24] |
李新勇, 赵志平, 王华栋, 等. 螺纹实用手册[M]. 北京: 机械工业出版社, 2009. LI Xinyong, ZHAO Zhiping, WANG Huadong, et al. Thread practical handbook[M]. Beijing: Mechanical Industry Press, 2009. |
 2020, Vol. 42
2020, Vol. 42


