2. 低渗透油气田勘探开发国家工程实验室, 陕西 西安 710018
2. National Engineering Laboratory for Exploration and Development of Low-permeability Oil & Gas Fields, Xi'an, Shaanxi 710018, China
储气库具有采气时间短、工作气量大的特点。采气时间通常在2~3月,而工作气量却占到储气库地质储量的20%~40%,折算后采气速度超过80%[1-7]。因此,想要在如此短的时间内采出大量的气体,提高气井的采气能力是储气库建库的关键。特别是利用非均质气藏建立的储气库,由于储层物性的差异,不同区域内气井产气能力不同,可以通过提高高渗区的井网密度,充分发挥高渗区产能优势,进而提高储气库的工作气量;但高渗区的井网密度如果过大,必然会加剧井间干扰,高渗区气井产能反而不如低渗区。所以,如何确定高、低渗区合理的井网密度,是非均质气藏储气库布井方式研究的核心问题。
本文以苏A储气库布井方式为例,根据建库区储层物性展布特征、气井产能和泄流范围评价结果,将建库区划分为两个区域,利用不同区域气井的实际生产数据,论证了不同区域气井的采气能力以及区域工作气量随采气井数的变化规律,同时,提出了一种基于工作气量最大化的非均匀布井方式,确定了高渗区、低渗区合理的井网密度。
1 苏A储气库基本地质特征苏A储气库位于鄂尔多斯乌审旗境内,区域处于平缓西倾单斜构造下的大型鼻隆部位,为岩性气藏(图 1),含气面积为21.2 km2,主要产层为马家沟组马五5段,埋藏深度3 100~3 160 m。
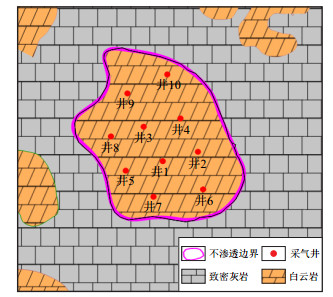 |
| 图1 苏A储气库建库区域岩性分布图 Fig. 1 The lithology distribution map of the area in Su A gas storage |
受沉积环境影响,储层物性表现出较强的非均质性。其中,储层厚度由中部向四周逐渐变薄,中心气层最大厚度达到23 m,而边部区域气层厚度仅有8.3 m,图 2为苏A储气库建库区域南北向连井剖面。
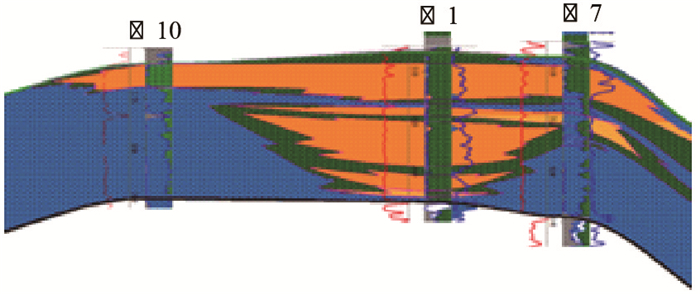 |
| 图2 苏A储气库建库区域南北向连井剖面 Fig. 2 The south-north connecting-well section of the area in Su A gas storage |
图 3为苏A储气库建库区域东西向连井剖面。图 4为苏A储气库区域孔隙度分布柱状图,苏A储气库地层岩石孔隙度和渗透率由区域中部向四周逐渐减小,中心区域平均孔隙度为10.1%,渗透率为35.1 mD,而边部区域孔隙度仅有7.2%,渗透率为9.2 mD。
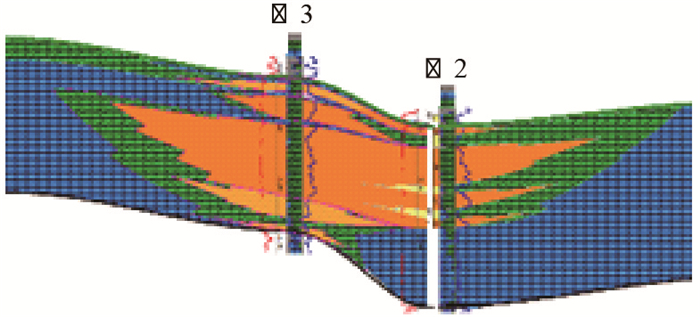 |
| 图3 苏A储气库建库区域东西向连井剖面 Fig. 3 The east-west connecting-well section of the area in Su A gas storage |
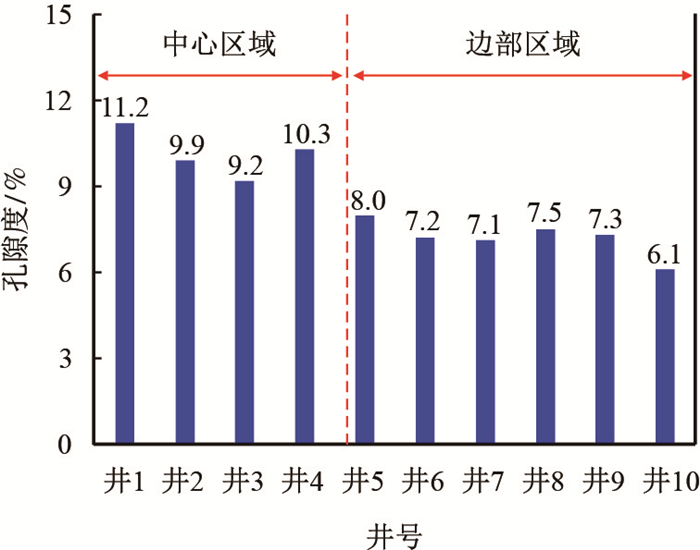 |
| 图4 苏A储气库孔隙度分布柱状图 Fig. 4 Porosity distribution chart in Su A gas storage |
图 5为苏A储气库渗透率分布柱状图。
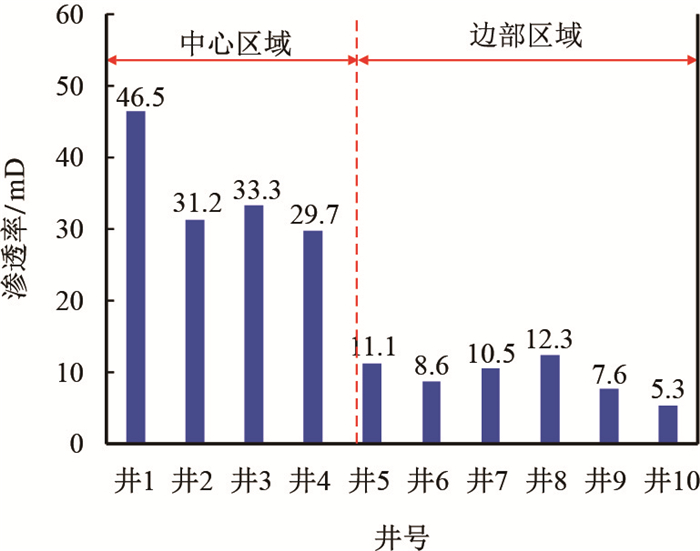 |
| 图5 苏A储气库渗透率分布柱状图 Fig. 5 Permeability distribution chart in Su A gas storage |
气井采气能力评价是论证储气库工作气量的基础,本文采用节点分析法,利用气井二项式产能方程和垂直管流计算公式[8-16],评价了建库区域内10口气井在不同地层压力下的产气能力,评价结果见表 1。
| 表1 不同地层压力下气井协调产量表 Tab. 1 Coordinate production table of gas wells under different formation pressures |
气井产能评价结果显示,受储层非均质性影响,气井产能分布具有明显的区域性,在原始地层压力下,中心区域气井产能超过90×104 m3/d,而外围气井产能最大仅52×104 m3/d左右。
3 建库区域分区产能评价考虑建库区气井间产能差异较大,并且具有明显的区域性,因此可以对气井产能进行分区评价。利用现代产量递减分析方法[17],计算了建库区域内10口气井的泄流范围:中心区域井1~井4分别为643,580,571,568 m;边部区域井5~井10分别为427,411,407,438,421,391 m。由于储层物性好,中心区域气井平均泄流半径可以达到590.5 m,而边部区域气井因储层物性限制,泄流半径略小,平均约为415.8 m。
在单井泄流范围评价基础上,将建库区由中心向四周划分为高渗、低渗两个区域,以建库区中心4口高产能气井泄流范围为基础,绘制高、低渗区边界(图 6)。分区后高渗区面积4.0 km2,储量12.1×108 m3;低渗区面积10.5 km2,储量12.6×108 m3。
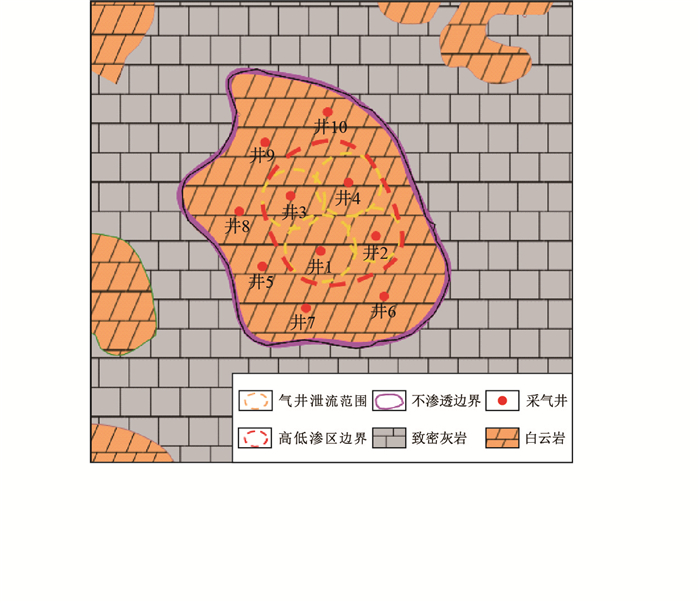 |
| 图6 气井泄流范围评价结果表 Fig. 6 Evaluation result table of gas well discharge scop |
根据气井产能评价结果,分别绘制了不同区域气井协调产量平均值与地层压力的关系曲线(图 7)。
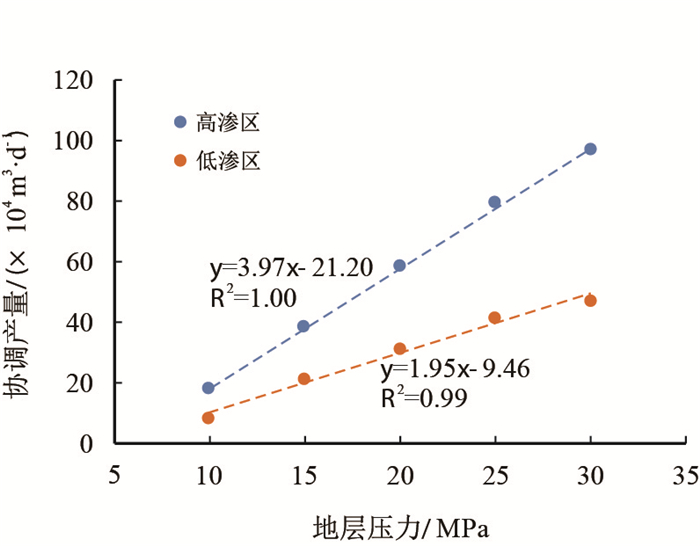 |
| 图7 气井合理产量与地层压力关系曲线图 Fig. 7 Relationship diagram between reasonable production and formation pressure |
结果表明,随着地层压力降低,气井产气能力逐渐降低,并且在同一地层压力下高渗区气井产气能力明显高于低渗区。
4 区域工作气量评价区域工作气量是指区域内所有气井在一个采气周期内的采气量之和。它反映了储气库运行过程中区域的实际调峰能力。对于苏A储气库,由于储层具有一定非均质性,不同区域气井产气能力不同,因此,相同采气井数下,不同区域的工作气量应有所不同。
4.1 区域工作气量计算方法以高渗区工作气量计算为例。高渗区原始地层压力30 MPa,原始地质储量12.1×108 m3,根据物质平衡原理[18-25],采气第i天,高渗区地层压力与区域累计采气量关系为
| $ \dfrac{{{p}_{i}}}{{{Z}_{i}}}=\dfrac{{\rm 30}}{Z}\left( {\rm 1-}\dfrac{{{G}_{i-1}}}{{\rm 12.1}} \right) $ | (1) |
式中:pi-采气第i天的地层压力,MPa;
Gi-1-采气第i-1天的高渗区累计采气量,×108 m3;
Z,Zi-原始地层压力下偏差系数、目前地层压力下偏差系数,无因次。
根据不同区域气井产能评价结果(图 7),采气第i天,高渗区气井采气能力与地层压力存在如下关系
| $ {{q}_{i}}={\rm 3.97}{{p}_{i}}-{\rm 21.2} $ | (2) |
式中:
qi-采气第i天气井的日产气能力,×104 m3。
采气第i天,高渗区累计采气量Gi与日产气量存在如下关系
| $ {{G}_{i}}={10^4}N\sum\limits_i {{q_i}} $ | (3) |
式中:
N-高渗区采气井数,口。
将式(1)、式(2)代入式(3)后,得到采气第i天高渗区累计采气量Gi计算公式为
| $ {{G}_{i}}={10^4}N\sum\limits_i {\left( {\rm 119.1}\dfrac{{{Z}_{i}}}{Z}-{\rm 9.84}\dfrac{{{Z}_{i}}}{Z}{{G}_{i-{\rm 1}}}-{\rm 21.2} \right)} $ | (4) |
式(4)中,采气第i天高渗区累计采气量Gi与采气第i-1天累计采气量Gi-1存在一定函数关系,由已知条件可知,采气第0天高渗区累计采气量G0为0,利用式(4),可以逐一计算出高渗区第1天、第2天以及采气任意一天区域累计采气量。按照定义,高渗区工作气量就是采气最后一天高渗区的累计采气量。假设该区域有采气井数为4口,储气库采气天数为120 d,按照式(4)计算得出高渗区工作气量为3.75×108 m3。
根据低渗区储量、原始地层压力以及气井产能评价结果,按照同样的方法,可以得到低渗区累计采气量G′i计算公式(式5),进而可以求出低渗区在不同采气井数下的工作气量。
| $ {{G}^{\prime }}_{i}={10^4}N\sum\limits_i{\left( {\rm 58.5}\dfrac{{{Z}_{i}}}{Z}-{\rm 4}{\rm .64}\dfrac{{{Z}_{i}}}{Z}{{{{G}'}}_{i-{\rm 1}}}-{\rm 9.46} \right)} $ | (5) |
式中:
G'i-采气第i天的低渗区累计采气量,×108 m3。
4.2 采气井数对区域工作气量的影响按照上述区域工作气量计算方法,假设苏A储气库采气天数为120 d,给定不同的采气井数,利用式(4)、式(5),分别绘制了高渗区、低渗区工作气量与采气井数的关系曲线(图 8)。
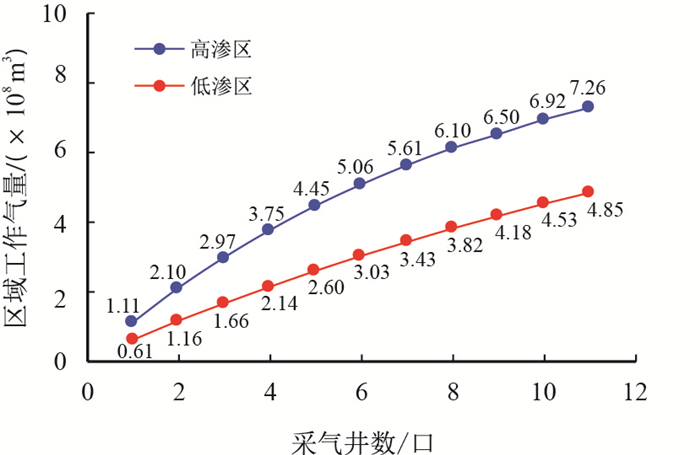 |
| 图8 高低渗透区工作气量与采气井数关系曲线图 Fig. 8 Graph of working gas volume and number of wells in high and low permeability areas |
结果显示,随着采气井数增加,高渗区、低渗区工作气量逐渐增大,但工作气量增加的速率逐渐减缓。其中,当低渗区采气井数较少时,每增加一口采气井,工作气量平均增加0.50×108 m3;当采气井数达到10口时,每增加一口采气井,低渗区工作气量增量为0.32×108 m3。
与低渗区相比,高渗区在采气井数较少时,每增加一口采气井,工作气量增量为1.0×108 m3。当采气井数为10时,每增加一口采气井,高渗区工作气量增量为0.39×108 m3。
5 布井方式优化设计与常规气田开发追求采收率不同,储气库建设追求的目标是气库工作气量,即不同区域工作气量之和。由于区域工作气量随着采气井数变化,在不同的采气井数下,高渗区和低渗区工作气量有所差异,所以,选择不同的布井方式,高渗区和低渗区的采气井数不同,储气库最终的工作气量也会有所不同。下面分别评价均匀布井和非均匀布井方式对储气库工作气量的影响。
5.1 均匀布井方式下储气库工作气量评价均匀布井方式下,建库区域各处的井网密度是相同的。根据区域划分结果,苏A储气库高渗区面积为4.0 km2、低渗区面积为10.5 km2,若采用均匀布井方式,按照面积比例,高渗区与低渗区部署气井的井数比例是1.0:2.6。任意给定储气库采气总数,按照井数比例,可以得到不同区域内各自部署的采气井数,再结合区域工作气量与采气井数关系,就可以计算出不同采气井数下储气库的工作气量(图 9)。
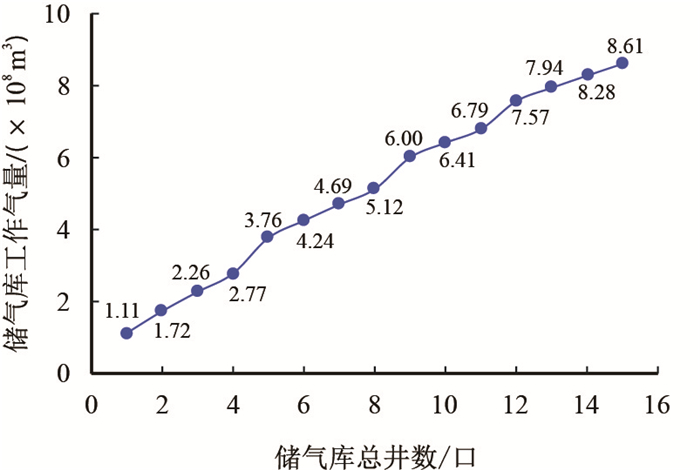 |
| 图9 均匀布井方式下储气库工作气量与总井数关系曲线图 Fig. 9 The relationship between the working gas volume of gas storage and the total number of wells in uniform well pattern |
非均匀布井方式下,不同建库区域的井网密度可以取不同的数值,考虑到储气库采气具有时间的限制,在同样的采气井数下,气井应优先部署在能最大幅度提高气库工作气量的区域内。根据高渗区、低渗区工作气量与采气井数的关系曲线,分别计算出在不同井数条件下,高渗区、低渗区各自新增加一口采气井,气库工作气量可以增加的气量(图 10)。
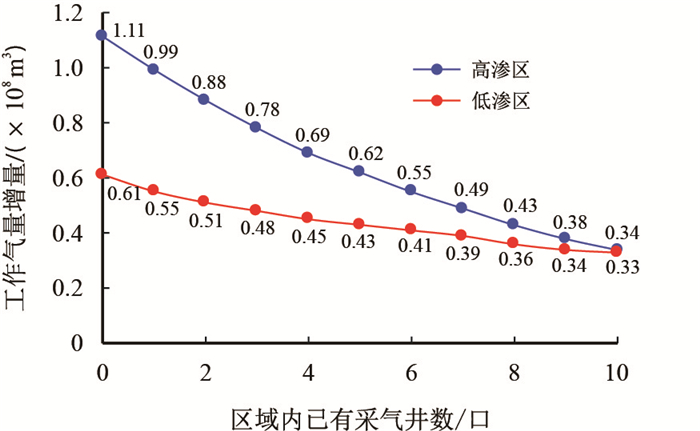 |
| 图10 高低渗透区域新增一口采气井时气库工作气量增量曲线 Fig. 10 The increment curve of working gas volume when a new gas well was added to the high and low permeability areas |
计算表明,新增采气井提高储气库工作气量的能力与区域内已有的采气井数有关。例如,当高渗区和低渗区已有采气井数分别为3口、1口时,高渗区和低渗区各自新增一口采气井,气库工作气量增量分别为0.78×108 m3、0.55×108 m3,为了保证气库工作气量最大化,此时储气库新增气井应该部署在高渗区。但是,当高渗区和低渗区已有采气井数分别为7口、1口时,高渗区和低渗区新增一口井,气库工作气量增量分别为0.49×108 m3、0.55×108 m3,此时,储气库新增气井应该部署在低渗区。
基于工作气量最大化的原则,非均匀布井方式应该根据高、低渗区域目前已有采气井数下,储气库新增加一口采气井提高工作气量的大小,逐一确定每一口采气井的部署区域。本文设计了非均匀布井方式下气库工作气量和采气井数计算流程,如图 11所示,具体包含以下几个步骤:
 |
| 图11 非均匀布井方式下气库工作气量和采气井数计算流程图 Fig. 11 Flow chart of working gas volume of gas storage and number of wells in non-uniform well pattern |
(1) 给定储气库建设的总井数为N,设定高渗区部署井数N1、低渗区部署井数N2、气库工作气量Q工作的初始值为0;
(2) 根据不同区域新增一口采气井气库工作气量增量曲线,计算在当前井数N1、N2条件下,高渗区新增一口采气井气库工作气量可以增加的气量ΔQ1和低渗区新增一口采气井,气库工作气量可以增加的气量ΔQ2;
(3) 判断ΔQ1、ΔQ2的大小,若ΔQ1>ΔQ2,则新增气井应部署在高渗区,计算Q工作=Q工作+ΔQ1、N1=N1+1;若ΔQ1 < ΔQ2,则新增气井应部署在低渗区,计算Q工作=Q工作 +ΔQ2、N2=N2+1;
(4) 判断N、N1+N2大小,若N>N1+N2,则根据N1、N2最新值,返回步骤(2)重新计算;若N ≤ N1+N2,则输出Q工作、N1、N2。
按照上述流程,将储气库采气总井数N由1逐渐增加,就可以计算不同采气井数下,储气库的工作气量和高渗区、低渗区分别应该部署的采气井数,计算结果如图 12。
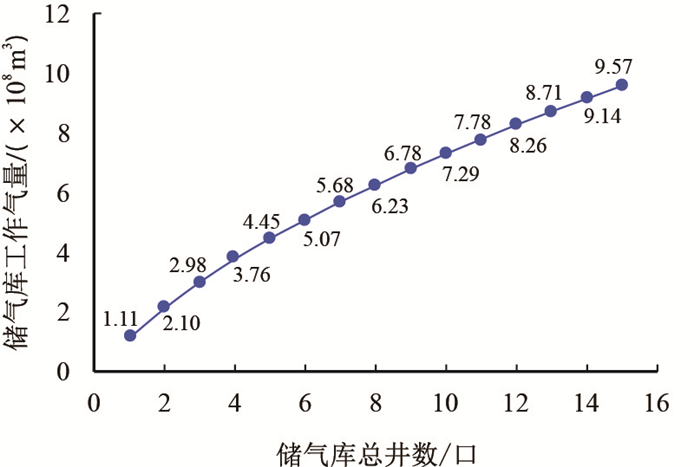 |
| 图12 非均匀布井方式下储气库工作气量与气库总井数关系曲线图 Fig. 12 The relationship between the working gas volume and the total number of wells in non-uniform well pattern |
通过对比,在储气库总采气井数相同的情况下,非均布井方式更有利于提高储气库工作气量(图 13);例如假设苏A储气库总采气井数为11口,若采用均匀布井方式,储气库工作气量为6.79×108 m3,若采用非均匀布井方式,储气库工作气量为7.78×108 m3,与均匀布井方式相比,工作气量提高了0.99×108 m3,提高幅度为14.6%。
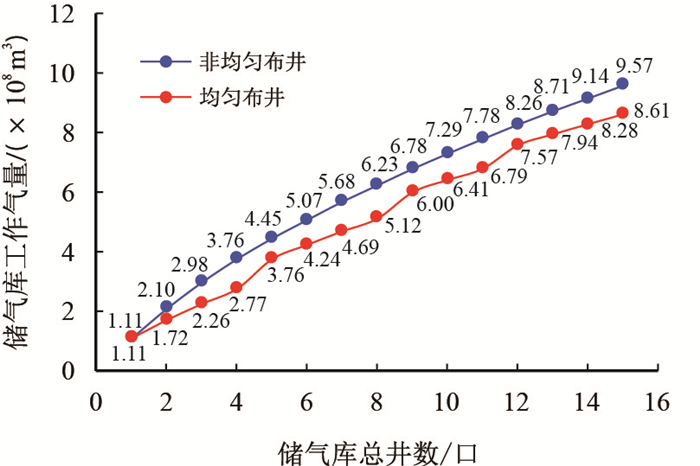 |
| 图13 不同布井方式下储气库工作气量对比图 Fig. 13 The comparison diagram of the working gas volume of gas storage with different well patterns |
与均匀井网布井方式相比,非均匀布井方式将更多的气井部署在高渗区内:当储气库采气井数为11口时,高渗区采气井达7口,井网密度1.70口/km2;而均匀布井方式下,高渗区采气井数只有3口,井网密度0.38口/ km2。相比之下,非均匀布井方式更有利于发挥高渗区高产能的优势,从而获得更大的工作气量。这也表明,对于非均质气藏储气库,应该采用非均匀布井方式,在一定程度上,提高高渗区的井网密度,发挥高渗区产能优势,利用较少采气井数获得更高的工作气量。
6 结论(1) 苏A储气库建库区域储层物性和气井产能具有区域性的特点,其高渗区气层厚度最大可达23 m,平均孔隙度为10.1%,渗透率为35.1 mD,气井初期产能为97×104 m3/d;与之相比,低渗区气层厚度只有8.3 m,孔隙度仅有7.2%,渗透率为9.2 mD,气井初期产能为45×104 m3/d。
(2) 新建采气井提高储气库工作气量的能力与区域内已有的采气井数有关,井数越多,新建井提高储气库工作气量的增量越小。
(3) 针对非均质气藏储气库,基于工作气量最大化原则,提出了一种非均匀布井方式。与均匀布井方式相比,非均布井方式更有利于提高储气库工作气量。
(4) 以苏A储气库为例,气库总采气井为11口时,采用非均匀布井方式,高渗区部署7口采气井,低渗区部署4口采气井,储气库工作气量可以达到7.78×108 m3,与均匀布井方式相比,工作气量提高了0.99×108 m3,提高幅度为14.6%。
| [1] |
刘志军, 兰义飞, 冯强汉, 等. 低渗岩性气藏建设地下储气库工作气量的确定[J]. 油气储运, 2012, 31(12): 891-894. LIU Zhijun, LAN Yifei, FENG Qianghan, et al. The determination of working gas volume of underground gas storage constructed for low permeability lithologic gas reservoirs[J]. Oil & Gas Storage and Transportation, 2012, 31(12): 891-894. doi: 10.6047/j.issn.1000-8241.2012.12.004 |
| [2] |
孙岩, 朱维耀, 刘思良, 等. 边水凝析气藏型储气库多周期工作气量计算方法[J]. 油气储运, 2018, 37(5): 509-514. SUN Yan, ZHU Weiyao, LIU Siliang, et al. A calculation method for the multi-cycle working gas volume of underground gas storage rebuilt from condensate gas reservoir with edge water[J]. Oil & Gas Storage and Transportation, 2018, 37(5): 509-514. doi: 10.6047/j.issn.1000-8241.2018.05.005 |
| [3] |
王皆明, 朱亚东. 确定地下储气库工作气量的优化方法[J]. 天然气工业, 2005, 25(12): 10.104. WANG Jieming, ZHU Yadong. Optimization method for determining working gas volume of underground gas storage[J]. Natural Gas Industry, 2005, 25(12): 10.104. doi: 10.3321/j.issn:1000-0976.2005.12.034 |
| [4] |
马小明, 赵平起. 地下储气库设计实用技术[M]. 北京: 石油工业出版社, 2009: 36-39. MA Xiaoming, ZHAO Pingqi. Practical technology for underground gas storage design[M]. Beijing: Petroleum Industry Press, 2009: 36-39. |
| [5] |
郑得文, 王皆明, 丁国生, 等. 气藏型储气库注采运行优化技术[M]. 北京: 石油工业出版社, 2018. ZHENG Dewen, WANG Jieming, DING Guosheng, et al. Optimization technology for injection and production operation of underground gas storage[M]. Beijing: Petroleum Industry Press, 2018. |
| [6] |
李建中, 李奇. 油气藏型地下储气库建库相关技术[J]. 天然气工业, 2013, 33(10): 10.103. LI Jianzhong, LI Qi. Related technologies in the construction of underground gas storage upon oil and gas reservoirs[J]. Natural Gas Industry, 2013, 33(10): 10.103. doi: 10.3787/j.issn.1000-0976.2013.10.017 |
| [7] |
胥洪成, 王皆明, 屈平, 等. 复杂地质条件气藏储气库库容参数的预测方法[J]. 天然气工业, 2015, 35(1): 10.108. XU Hongcheng, WANG Jieming, QU Ping, et al. A prediction model of storage capacity parameters of a geologically-complicated reservoir-type underground gas storage (UGS)[J]. Natural Gas Industry, 2015, 35(1): 10.108. doi: 10.3787/j.issn.1000-0976.2015.01.014 |
| [8] |
郑得文, 胥洪成, 王皆明, 等. 气藏型储气库建库评价关键技术[J]. 石油探勘与开发, 2017, 44(5): 794-801. ZHENG Dewen, XU Hongcheng, WANG Jieming, et al. Key evaluation techniques in the process of gas reservoir being converted into underground gas storage[J]. Petroleum Exploration and Development, 2017, 44(5): 794-801. doi: 10.11698/PED.2017.05.15 |
| [9] |
梁涛, 郭肖, 付德奎, 等. R油藏改建地下储气库单井注采能力分析[J]. 西南石油大学学报, 2007, 29(6): 157-160. LIANG Tao, GUO Xiao, FU Dekui, et al. Analysis on injection-production capability of single well in R gas storage[J]. Journal of Southwest Petroleum University, 2007, 29(6): 157-160. doi: 10.3863/j.issn.1674-5086.2007.06.039 |
| [10] |
阳小平, 程林松, 何学良, 等. 地下储气库多周期运行注采气能力预测方法[J]. 天然气工业, 2013, 33(4): 96-99. YANG Xiaoping, CHENG Linsong, HE Xueliang, et al. A prediction method for multi-stage injection and recovery capacity of underground gas storage[J]. Natural Gas Industry, 2013, 33(4): 96-99. doi: 10.3787/j.issn.1000-0976.2013.04.017 |
| [11] |
许珍萍.枯竭气藏地下储气库注采系统数值模拟及参数优化[D].成都: 西南石油大学, 2012: 29-32. XU Zhenping. Numerical simulation and parameter optimization of depleted underground gas storage productioninjection system[D]. Chengdu: Southwest Petroleum University, 2012: 29-32. |
| [12] |
陈显学, 温海波. 辽河油田双6储气库单井采气能力评价[J]. 新疆石油地质, 2017, 38(6): 715-718. CHEN Xianxue, WEN Haibo. Evaluation of single gas well production capacity of Shuang-6 gas storage in Liaohe Oilfield[J]. Xinjiang Petroleum Geology, 2017, 38(6): 715-718. doi: 10.7657/XJPG20170613 |
| [13] |
姜永清. 储气库产能的节点分析方法W23储气库实例[J]. 化工管理, 2015(14): 199. JIANG Yongqing. Node analysis method of gas storage capacity:An example of W23 gas storage[J]. Chemical Enterprise Management, 2015(14): 199. doi: 10.3969/j.issn.1008-4800.2015.14.165 |
| [14] |
李君, 王源. 气井节点分析方法及其应用[J]. 油气井测试, 2012, 21(6): 28-30. LI Jun, WANG Yuan. Gas well nodal analysis method and application[J]. Well Testing, 2012, 21(6): 28-30. doi: 10.3969/j.issn.1004-4388.2012.06.010 |
| [15] |
胥洪成, 董宏, 吕建, 等. 水侵枯竭气藏型储气库运行初期合理配注方法[J]. 天然气工业, 2017, 37(2): 92-96. XU Hongcheng, DONG Hong, LÜ Jian, et al. An approach to rational injection allocation of UGSs rebuilt from watered-out depleted gas reservoirs during initial operation[J]. Natural Gas Industry, 2017, 37(2): 92-96. doi: 10.3787/j.issn.1000-0976.2017.02.012 |
| [16] |
陈元千. 气井垂直管流计算方法的推导与应用[J]. 断块油气藏, 2010, 17(4): 443-447. CHEN Yuanqian. Derivation and application of calculating methods of vertical pipe flow in gas wells[J]. FaultBlock Oil and Gas Reservoir, 2010, 17(4): 443-447. |
| [17] |
刘刚. 现代产量递减分析技术在敖南气井中的应用[J]. 石油化工应用, 2019, 38(6): 41-44, 57. LIU Gang. Application of modern production decline analysis technology in Aonan gas well[J]. Petrochemical Industry Application, 2019, 38(6): 41-44, 57. doi: 10.3969/j.issn.1673-5285.2019.06.009 |
| [18] |
温凯, 何蕾, 虞维超, 等. 枯竭油气藏型储气库地层压力的计算方法[J]. 油气储运, 2017, 36(7): 781-788. WEN Kai, HE Lei, YU Weichao, et al. Calculation methods on formation pressure of underground gas storage rebuilt from depleted oil and gas reservoir[J]. Oil & Gas Storage and Transportation, 2017, 36(7): 781-788. doi: 10.6047/j.issn.1000-8241.2017.07.006 |
| [19] |
于本福, 闫相祯, 杨秀娟, 等. 考虑储层孔隙介质分形特点的衰竭气藏储气库储层压力分布预测[J]. 石油学报, 2013, 34(5): 1017-1022. YU Benfu, YAN Xiangzhen, YANG Xiujuan, et al. Dynamic reservoir pressure prediction of depleted reservoir gas storage considering the fractal feature of porous medium[J]. Acta Petrolei Sinica, 2013, 34(5): 1017-1022. doi: 10.7623/syxb201305026 |
| [20] |
张立侠, 郭春秋, 蒋豪, 等. 物质平衡拟压力近似条件法确定气藏储量[J]. 石油学报, 2019, 40(3): 337-349. ZHANG Lixia, GUO Chunqiu, JIANG Hao, et al. Gas in place determination by material balance quasipressure approximation condition method[J]. Acta Petrolei Sinica, 2019, 40(3): 337-349. doi: 10.7623/syxb201903008 |
| [21] |
王保辉, 闫相祯, 杨秀娟, 等. 含水层型地下储气库天然气动态运移规律[J]. 石油学报, 2012, 33(2): 58-61. WANG Baohui, YAN Xiangzhen, YANG Xiujuan, et al. Natural gas dynamic migration in an underground gas storage in aquifer beds[J]. Acta Petrolei Sinica, 2012, 33(2): 58-61. doi: 10.3969/j.issn.1671-4067.2012.02.020 |
| [22] |
胥洪成, 李娟, 李宏春, 等. 大港储气库群达容的主要影响因素[J]. 科技导报, 2011, 29(16): 58-61. XU Hongcheng, LI Juan, LI Hongchun, et al. Main influencing factors of capacity of Dagang underground gas storage facilities[J]. Science and Technology Review, 2011, 29(16): 58-61. doi: 10.3981/j.issn.1000-7857.2011.16.008 |
| [23] |
石磊, 王皆明, 廖广志, 等. 水驱气藏型储气库运行指标动态预测[J]. 中南大学学报(自然科学版), 2013, 44(2): 701-706. SHI Lei, WANG Jieming, LIAO Gangzhi, et al. Dynamic prediction of operation indexes of flooded gas storage[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 701-706. |
| [24] |
唐立根, 王皆明, 白凤娟, 等. 基于修正后的物质平衡方程预测储气库库存量[J]. 石油勘探与开发, 2014, 41(4): 480-484. TANG Ligen, WANG Jieming, BAI Fengjuan, et al. Inventory forecast in underground gas storage based on modified material balance equation[J]. Petroleum Exploration and Development, 2014, 41(4): 480-484. doi: 10.11698/PED.2014.04.14 |
| [25] |
辛翠平, 王永科, 徐云林, 等. 修正的流动物质平衡法计算致密气藏动态储量[J]. 特种油气藏, 2018, 25(2): 95-98. XIN Cuiping, WANG Yongke, XU Yunlin, et al. Tight gas reservoir dynamic reserve calculation with modified flowing material balance[J]. Special Oil & Gas Reservoirs, 2018, 25(2): 95-98. doi: 10.3969/j.issn.1006-6535.2018.02.018 |
 2020, Vol. 42
2020, Vol. 42


