直井开发无夹层发育稠油底水油藏时,不可避免地会形成底水锥进。经过长期大液量的冲刷,在水锥锥体内部不同区域,储层孔隙度、渗透率、黏土矿物含量以及孔喉结构等发生很大的变化。而在水锥锥体之外,储层基本上处于原始状态。
对底水油藏而言,水锥的精细刻画是认识底水油藏剩余油的核心,若能准确描述高含水阶段水锥的变化规律,就能确定剩余油富集甜点区,为油田挖潜提供支撑。针对如何准确描述水锥变化,许多学者进行了大量的研究。文献[1]中,朱圣举认为水锥是侧面为直线的线性锥,推导了底水油藏水锥计算公式,而李传亮认为水锥是曲面锥,并推导了水锥侧面为曲面的水锥表达公式。侯君等基于静力学原理,建立了油层不同打开程度时的水锥高度分布模型,认为在近井地带水锥变化比较明显[2]。谷建伟等利用数值模拟方法回归了无夹层模式下的水锥定量描述公式[3]。唐人选等利用平面径向流和半球状向心流的组合,通过假设不同的边界条件,重新推导了考虑原始油水界面处压力随产量变化的临界产量和水锥高度计算公式[4-6]。黄咏梅等认为碳酸盐岩油藏油井产液量的变化对水锥影响很大,建立了基于液量变化的水锥高度计算模型[7]。杨元亮等认为沿井筒近井地带水淹严重,采用数值模拟方法对氮气泡沫压锥进行探索,提出了氮气压水锥的方法[8]。赵燕等利用实际动态参数建立了水驱特征曲线与直井水锥变化的关系式,体现了水锥的动态认识[9-11]。但是,针对大液量冲刷后储层物性变化引起的水锥变化规律研究还处于探索阶段,许多学者讨论了物性时变引起的含油饱和度的变化以及物性时变在数值模拟中的应用[12-15]。笔者考虑了长期大液量冲刷后储层物性的变化,通过对水锥内部各区域储层渗透率以及水锥外部渗透率进行等效表征,重新推导了水锥高度定量计算公式。
1 转注井水锥变化数学模型建立 1.1 高倍数冲刷下储层物性变化规律通过文献调研[16-20],模拟岩芯经过高倍数(2 000 PV)液量的驱替,蒙脱石,伊/蒙混层等胶结物被带出,导致孔喉结构改变,表现为低渗储层渗透率减小,高渗储层渗透率增大。
压汞实验证实[21-24],长期大液量冲刷后,储层孔隙度较初始状态增大8%~10%,渗透率较初始状态增大50%~200%,孔喉半径中值增大60%~90%[25]。结合邻眼井测井资料统计,强水淹层的渗透率增大了两倍,尤其是在定向井近井地带,渗透率较原始状态增大5倍以上。
综合来看,经过长期大液量冲刷后,储层物性变化规律为:水锥外未被冲刷的区域渗透率处于原始状态。水锥内定向井底部强冲刷区渗透率增幅最大,靠近水锥边部随着冲刷强度减弱渗透率增幅逐渐减小;纵向上,定向井越靠近油层顶面,渗透率增幅逐渐降低[25]。定向井井控范围内渗透率分布见图 1。
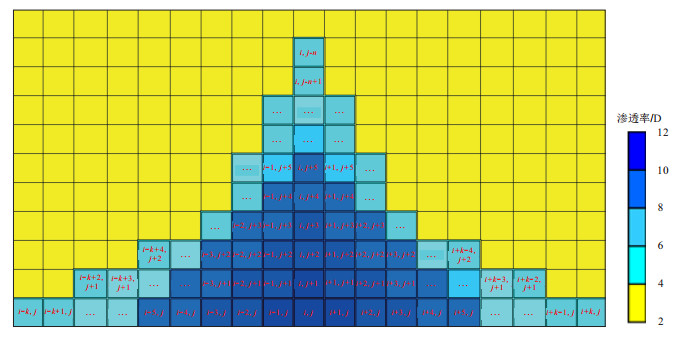 |
| 图1 定向井沿井筒储层物性变化网格示意图 Fig. 1 Grid diagram of directional well along wellbore reservoir physical property change |
流体受正韵律、重力等因素的影响,纵向上沿井筒可以看成若干小层的并联,流体在每个小层平面上的渗流可以看成若干小层的串联,每个网格内的流动分为平面和纵向两个方向渗流的组合[26]。图 2是流体在纵向和平面的流动示意图。
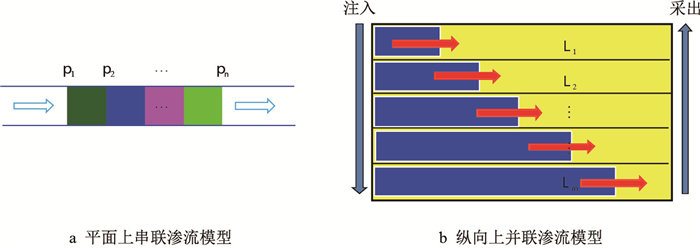 |
| 图2 流体渗流示意图 Fig. 2 Schematic diagram of fluid seepage |
流体在水平方向上流经路线相当于多重介质的串联(图 2a)。
假设有宽为W,高为h,长度分别为L1,L2,..., Ln,水平渗透率分别为K1,K2,...,Kn的不同储层带,在驱替压差的作用下,黏度为μ的流体平面线形渗流,求地层总平均渗透率K。这种流动相当于各储层段串联,即通过各层的流量Q相等,总压差Δp为各层压差之和:Δp=Δp1+ Δp2+... + Δpn,地层总的延伸长度L为各层长度之和:L=L1+L2+...+Ln。
根据达西定律及总压差等于各层压差之和的关系,得到平面上每个小层的等效渗透率,如式(1)所示
| $ {{K}_{x}}=\dfrac{{{L}_{1}}+{{L}_{2}}+... +{{L}_{n}}}{\dfrac{{{L}_{1}}}{{{K}_{1}}}+\dfrac{{{L}_{2}}}{{{K}_{2}}}+... +\dfrac{{{L}_{n}}}{{{K}_{n}}}} = \dfrac{\sum\limits_{i=1}^{n}{{{L}_{i}}}}{\sum\limits_{i=1}^{n}{\dfrac{{{L}_{i}}}{{{K}_{i}}}}}, {\kern 13pt}i=1, 2, ..., n $ | (1) |
流体在纵向上流经路线相当于多重介质的并联(图 2b)。
假设有宽为W,长度为L,高度分别为H1,H2,...,Hm,垂向渗透率分别为K1,K2,...,Km的不同储层带(图 2b),在驱替压差的作用下,黏度为μ的流体平面线形渗流,求地层总平均渗透率K。这种流动相当于各储层段并联,即通过各层的压差Δp相等,总流量Q为各层流量之和:Q=Q1+Q2+...+Qm,地层总厚度H为各层长度之和:H=H1+H2+...+Hm。
根据达西定律及总流量等于各层流量之和的关系,得到纵向上每个小层的等效渗透率(式2)
| $ {{K}_{{ y}}}=\dfrac{{{K}_{1}}{{H}_{1}}+{{K}_{2}}{{H}_{2}}+... +{{K}_{m}}{{H}_{m}}}{{{H}_{1}}+{{H}_{2}}+... +{{H}_{m}}}=\dfrac{\sum\limits_{j=1}^{m}{{{K}_{j}}{{H}_{j}}}}{\sum\limits_{j=1}^{m}{{{H}_{j}}}}, {\kern 13pt}j=1, 2, ..., m $ | (2) |
定向井纵向上沿井筒可以看成若干小层的并联,流体在每个小层平面上的渗流可以看成若干小层的串联。将式(1)代入式(2)可得沿定向井井筒渗透率变化关系式
| $ K=\dfrac{\sum\limits_{j=1}^{m}{{{\left( {{K}_{x}} \right)}_{j}}{{H}_{j}}}}{\sum\limits_{j=1}^{m}{{{H}_{j}}}} $ | (3) |
假设油藏为水平圆形均质底水油藏,有连续的油水界面,地下流体流动为稳定的平面径向流动[2]。圆形油藏中心一口定向井以流量Q稳定生产,在原始油水界面处有A、B两点,压力分别为pA、pB。在曲面锥的锥面上任取点1,点2,压力分别为p1'、p2',r1、r2为从井中心轴到锥面这两点的距离,f(r1)、f(r2)分别为两点对应的水锥高度,如图 3所示。
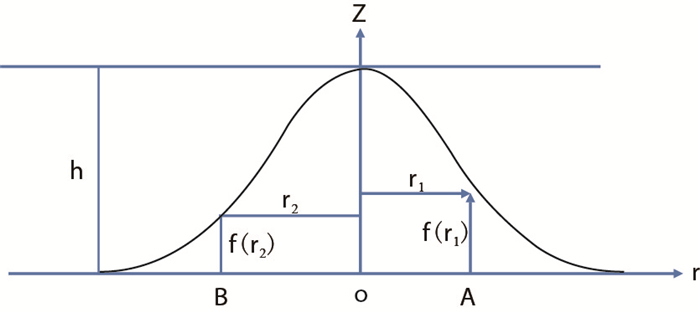 |
| 图3 定向井水锥示意图 Fig. 3 Directional well water cone diagram |
由静力学原理pA= pB,有
| $ {p_1}^\prime -{{p}_{{\rm c}}}+{{\rho }_{\rm w}}{\rm g}f({{r}_{1}})+{{\rho }_{\rm o}}{\rm g}\left[ f({{r}_{2}})-f({{r}_{1}}) \right]={{p_2}^\prime} -{{p}_{\rm c}}+{{\rho }_{\rm w}}{\rm g}f({{r}_{2}}) $ | (4) |
渗流速度
| $ v =\dfrac{{{Q}_{{\rm w}}}{{B}_{\rm w}}}{2πup r\left[ h'-f(r) \right]} $ | (5) |
将水锥锥体内外平面和垂向等效渗透率式(3)代入式(5),得出考虑大液量冲刷后储层物性变化的底水油藏转注井水锥变化关系式
| $ \dfrac{\partial f\left( r \right)}{\partial r}=\dfrac{{{μ }_{\rm w}}{{Q}_{\rm w}}{{B}_{\rm w}}}{2πup KΔ {{ρ }_{\rm w}}{\rm g}\left[ h'-f\left( r \right) \right]r} $ | (6) |
以渤海Q油田稠油底水油藏F7井为例,该井与104 m处的一口过路井J24P1井油层连井剖面见图 4。
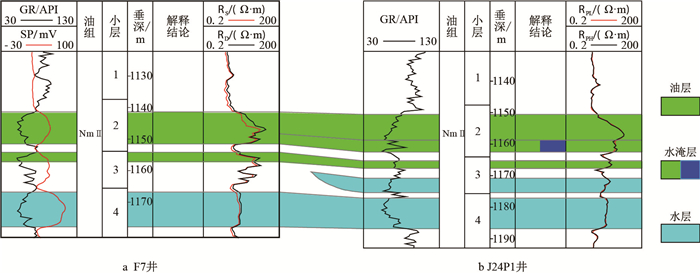 |
| 图4 渤海Q油田F7-J24P1井油层连井剖面图 Fig. 4 Well connection profile map of Well F7-J24P1 in Bohai Q Oilfield |
F7井地下原油密度为0.93 g/cm3,地下原油黏度为260 mPa·s,原油体积系数为1.645 m3/m3,水平渗透率为3 114 mD,垂向渗透率为1 421 mD,井筒半径为0.11 m,油层厚度为11.6 m,避射高度为3.5 m,生产压差为2.3 MPa。该井2002年8月投产,投产初期产液量为200 m3/d,2006年4月提液至600 m3/d,该井于2013年5月转注,转注前一直以产液量600 m3/d稳定生产,转注后累计注入180×104 m3。2017年8月,J24P1测井解释F7井所投产层位水淹高度3.8 m(图 4);而利用考虑物性时变性的水锥变化公式得到相同位置上的水锥高度为3.60 m,绝对误差为0.20 m,相对误差为5.3%。实钻过路井解释结果与计算结果对比,推导的考虑物性时变性的定向井水锥变化关系式计算结果与油田实钻结果一致。
通过统计渤海Q油田15口实钻过路井水淹情况与理论计算的水锥高度进行对比(表 1),其中,14口井水锥高度计算结果与实钻解释结果基本一致,符合率达到90%以上,证实了考虑物性时变的底水油藏定向井水锥变化关系的可靠性。
| 表1 理论计算与实钻解释结果对比统计表 Tab. 1 Comparison between theoretical calculation and actual drill interpretation results |
利用该实例对考虑物性时变的底水油藏转注井水锥变化关系式以及常规底水油藏定向井水锥变化式进行对比分析。
计算结果如图 5所示,水锥半径为100 m时,常规底水油藏定向井水锥公式计算的水锥高度是6.7 m,考虑物性时变的底水油藏水锥公式计算的水锥高度3.6 m,而过路井实钻测井解释为3.8 m,计算结果与测井解释最为接近,误差最小。通过研究分析可知,未考虑储层物性时变的底水油藏定向井水锥计算明显偏大,导致波及体积偏大,剩余油的认识偏悲观。
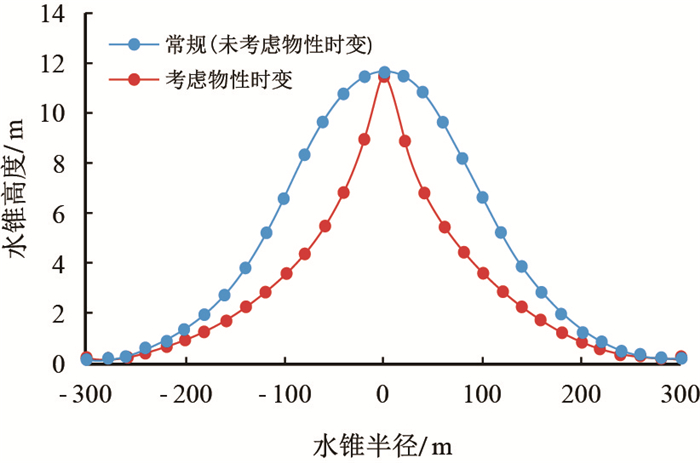 |
| 图5 不同条件下底水油藏定向井水锥变化对比 Fig. 5 Comparison of water cone changes in directional wells in bottom-water reservoirs under different conditions |
渤海Q油田稠油底水油藏局部区域目前注采井距为250~300 m,根据考虑物性时变性的稠油底水油藏定向井水锥变化关系,在目前井距下,水淹厚度仅占油层的30%左右,储层中上部剩余油处于未动用状态。在该技术的指导下,2017年5月-2018年11月,在注采井距为250~300 m区域内新转注定向井6口,单一井组井间加密井网变化见图 6,转注后受益油井平均单井日增油量12 m3,累计增油8.84×104 m3。
 |
| 图6 井间加密井网变化示意图 Fig. 6 Schematic diagram of inter-well infill pattern change |
通过对渤海Q油田定向井进行计算分析,认为采油井井距大于150 m和注采井距大于250 m的区域,剩余油富集程度高。在该技术的指导下,以累计产油5.0×104 m3为海上油田可布井经济界限,2018年1月-2018年11月,渤海Q油田部署调整井4口,投产初期平均日产油量55 m3,含水率为45%,目前已累计产出原油3.2×104 m3。
4 结论(1) 经过长期大液量冲刷后,生产井井点附近储层的物性变化非常明显,渗透率变化值达到原始渗透率的2~5倍。通过对长期冲刷后水锥渗透率进行等效表征,重新推导了考虑物性时变的稠油底水油藏定向井水锥变化关系式,其理论计算水淹高度与实钻过路井测井解释水淹高度一致。
(2) 与考虑物性时变性的底水油藏定向井水锥变化公式获得的水驱波及体积相比,以往未考虑物性时变性的底水油藏定向井水锥变化公式得到的波及体积偏大,导致井间剩余油认识偏悲观,无法充分释放油藏潜力。
(3) 矿场先导试验证实了考虑物性时变性的底水油藏定向井水锥变化公式的可靠性,为准确描述长期大液量冲刷下稠油底水油藏高含水阶段水锥变化及剩余油分布规律提供了技术支持。
符号说明
i-平面x向网格数;
j-平面y方网格数;
p1-流经平面上第1个网格进口端处的压力,MPa;
p2-流经平面上第2个网格进口端处的压力,MPa;
pn-流经平面上第n个网格进口端处的压力,MPa;
L1-平面上第1个网格的长度,m;
L2-平面上第2个网格的长度,m;
Ln-平面上第n个网格的长度,m;
W-网格宽度,m;
h-网格高度,m;
K1-第1个网格的渗透率,mD;
K2-第2个网格的渗透率,mD;
Kn-平面上第n个网格的渗透率,mD;
μ-黏度,mPa·s;
K-流体流经储层的等效渗透率,mD;
Q-流体流经储层的体积总流量,m3;
Δp-总压差,MPa;
Δp1-流体流经平面上第1个网格的压差,MPa;
Δp2-流体流经平面上第2个网格的压差,MPa;
Δpn-流体流经平面上第n个网格的压差,MPa;
L-由n个网格组成的储层长度,m;
Kx-平面上某小层的等效渗透率,mD;
H1-纵向第1个网格的厚度,m;
H2-纵向第2个网格的厚度,m;
Hm-纵向第m个网格的厚度,m;
Km-纵向第m个网格的渗透率,mD;
Q1-流体流经纵向第1个网格的体积流量,m3;
Q2-流体流经纵向第2个网格的体积流量,m3;
Qm-流体流经纵向第m个网格的体积流量,m3;
H-纵向上m个网格的储层厚度,m;
Ky-纵向某小层的等效渗透率,mD;
pA,pB-点A,点B处的压力,MPa;
p1',p2'-锥面上点1,点2处的压力,MPa;
r1,r2-从井中心轴到点1,点2距离,m;
f()-水锥高度函数,m;
r-水锥半径,m;
pc-油水界面处压力,MPa;
ρw-地层水密度,g/cm3;
g-重力加速度,g = 9.8 m/s2;
ρo-地下原油密度,g/cm3;
v-渗流速度,m/s;
Qw -地面体积流量,m3/d;
Bw -地层水体积系数,无因次;
h'-油层厚度,m;
μw-地层水黏度,mPa·s。
| [1] |
李传亮. 水锥形态分析与朱圣举先生商榷[J]. 新疆石油地质, 2002, 23(1): 74-75. LI Chuangliang. An analysis on water coing shape:A discussion with Mr. ZHU Shengju[J]. Xinjiang Petroleum Geology, 2002, 23(1): 74-75. doi: 10.3969/j.issn.1001-3873.2002.01.025 |
| [2] |
侯君, 程林松. 常规底水油藏水锥高度计算方法研究[J]. 西安石油大学学报, 2006, 21(3): 23-26. HOU Jun, CHENG Linsong. Calculation method for the water cone height of bottom-water reservoir[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2006, 21(3): 23-26. doi: 10.3969/j.issn.1673-064X.2006.03.006 |
| [3] |
谷建伟, 姜汉桥, 吴义志, 等. 无夹层底水油藏直井水锥定量描述[J]. 油气地质与采收率, 2012, 19(6): 78-81. GU Jianwei, JIANG Hanqiao, WU Yizhi, et al. Quantitative description of vertical well coning in bottom water reservoir with no interlayer[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(6): 78-81. doi: 10.13673/j.cnki.cn37-1359/te.2012.06.020 |
| [4] |
唐人选. 底水油藏水锥动态模拟及见水时间预测[J]. 新疆石油地质, 2003, 24(6): 572-573. TANG Renxuan. Dynamic simulation of water cone in bottom water reservoir and prediction of water seeing time[J]. Xinjiang Petroleum Geology, 2003, 24(6): 572-573. doi: 10.3969/j.issn.1001-3873.2003.06.026 |
| [5] |
蒋平, 张贵才, 何小娟, 等. 底水锥进的动态预测方法[J]. 钻采工艺, 2007, 30(2): 71-73. JIANG Ping, ZHANG Guicai, HE Xiaojuan, et al. Dynamic prediction method of bottom water coning[J]. Drilling & Production Technology, 2007, 30(2): 71-73. doi: 10.3969/j.issn.1006-768X.2007.02.024 |
| [6] |
蒋平, 张贵才, 葛际江, 等. 采用供给边界压力预测底水突破前水锥参数[J]. 油气地质与采收率, 2006, 13(6): 76-78. JIANG Ping, ZHANG Guicai, GE Jijiang, et al. Prediction of water cone parameters before bottom water breakthrough by supply boundary pressure[J]. Petroleum Geology and Recovery Efficiency, 2006, 13(6): 76-78. doi: 10.13673/j.cnki.cn37-1359/te.2006.06.023 |
| [7] |
黄咏梅, 王子胜. 产液量变化对水锥的作用机制[J]. 油气地质与采收率, 2008, 15(6): 83-85. HUANG Yongmei, WANG Zisheng. Mechanism of the change of liquid production on water cone[J]. Petroleum Geology and Recovery Efficiency, 2008, 15(6): 83-85. doi: 10.13673/j.cnki.cn37-1359/te.2008.06.025 |
| [8] |
杨元亮, 沈国华, 宋文芳, 等. 注氮气控制稠油油藏底水水锥技术[J]. 油气地质与采收率, 2002, 9(3): 83-84, 88. YANG Yuanliang, SHEN Guohua, SONG Wenfang, et al. Technology of controlling bottom water cone in heavy oil reservoir by N2 injection[J]. Petroleum Geology and Recovery Efficiency, 2002, 9(3): 83-84, 88. doi: 10.13673/j.cnki.cn37-1359/te.2002.03.027 |
| [9] |
赵燕, 陈向军. 底水油藏水锥回落高度预测模型[J]. 断块油气田, 2018, 25(3): 367-370. ZHAO Yan, CHEN Xiangjun. Prediction models of water cone falling height for bottom water reservoirs[J]. FaultBlock Oil & Gas Field, 2018, 25(3): 367-370. doi: 10.6056/dkyqt201803020 |
| [10] |
于登飞, 许亚南, 龙明, 等. 强底水油藏水平井见水时间及水锥动态研究[J]. 科学技术与工程, 2017, 17(28): 191-193. YU Dengfei, XU Ya'nan, LONG Ming, et al. Breakthrough time prediction and water coning shape dyna-mic simulation of horizontal well in strong bottom water reservoirs[J]. Science Technology and Engineering, 2017, 17(28): 191-193. doi: 10.3969/j.issn.1671-1815.2017.28.033 |
| [11] |
章威, 龙明, 李军, 等. 生产动态确定底水油藏油井水淹范围的新方法[J]. 天然气与石油, 2017, 35(4): 68-72. ZHANG Wei, LONG Ming, LI Jun, et al. A new method for determining the water flooded range of bottom water reservoir by production performance[J]. Natural Gas and Oil, 2017, 35(4): 68-72. doi: 10.3969/j.issn.1006-5539.2017.04.012 |
| [12] |
刘晨. 考虑储层参数时变的相对渗透率曲线计算方法[J]. 西南石油大学学报(自然科学版), 2019, 41(2): 137-142. LIU Chen. Method for calculating the relative permeability curve of an oil reservoir considering the timevarying effect of relevant reservoir parameters[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2019, 41(2): 137-142. doi: 10.11885/j.issn.16745086.2018.08.08.01 |
| [13] |
宁国卿, 王平, 徐建春, 等. 考虑储层渗透率时变的深部封堵数值模拟技术[J]. 科学技术与工程, 2012, 12(7): 1618-1620. NING Guoqing, WANG Ping, XU Jianchun, et al. Simulation technology of deep plugging considering formation dynamic permeability[J]. Science Technology and Engineering, 2012, 12(7): 1618-1620. doi: 10.3969/j.issn.1671-1815.2012.07.036 |
| [14] |
姜瑞忠, 乔欣, 滕文超, 等. 储层物性时变对油藏水驱开发的影响[J]. 断块油气田, 2016, 23(6): 768-771. JIANG Ruizhong, QIAO Xin, TENG Wenchao, et al. Impact of physical properties time variation on waterflooding reservoir development[J]. Fault-Block Oil & Gas Field, 2016, 23(6): 768-771. doi: 10.6056/dkyqt201606017 |
| [15] |
金忠康, 方全堂, 王磊, 等. 考虑储集层参数时变效应的数值模拟方法与应用[J]. 新疆石油地质, 2016, 37(3): 342-345. JIN Zhongkang, FANG Quantang, WANG Lei, et al. Numerical simulation method and its application when considering time-dependent effect of reservoir parameters[J]. Xinjiang Petroleum Geology, 2016, 37(3): 342-345. doi: 10.7657/xjpg20160319 |
| [16] |
钟大康, 朱筱敏, 吴胜和, 等. 注水开发油藏高含水期大孔道发育特征及控制因素以胡状集油田胡12断块油藏为例[J]. 石油勘探与开发, 2007, 34(2): 201-211. ZHONG Dakang, ZHU Xiaomin, WU Shenghe, et al. Characteristics and controlling factors of high capacity channels of reservoirs at high water cut stage:A case from Block Hu 12 of Huzhuangji Oilfield[J]. Petroleum Exploration and Development, 2007, 34(2): 201-211. doi: 10.3321/j.issn:1000-0747.2007.02.015 |
| [17] |
李浩, 王香文, 刘双莲. 老油田储层物性参数变化规律研究[J]. 西南石油大学学报(自然科学版), 2009, 31(2): 85-89. LI Hao, WANG Xiangwen, LIU Shuanglian. Variation law of parameters of reservoir physcial property in old oilfield[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(2): 85-89. doi: 10.3863/j.issn.1674-5086.2009.02.022 |
| [18] |
熊山, 王学生, 张遂, 等. WXS油藏长期水驱储层物性参数变化规律[J]. 岩性油气藏, 2019, 31(3): 120-129. XIONG Shan, WANG Xuesheng, ZHANG Sui, et al. Physical properties variation of WXS Reservoir after long-term water flooding[J]. Lithologic Reservoirs, 2019, 31(3): 120-129. doi: 10.12108/yxyqc.20190314 |
| [19] |
洪楚侨, 王雯娟, 鲁瑞斌, 等. 强水驱油藏渗透率动态变化规律定量预测方法[J]. 西南石油大学学报(自然科学版), 2018, 40(5): 113-121. HONG Chuqiao, WANG Wenjuan, LU Ruibin, et al. A quantitative method to predict the dynamic variation in permeability of oil reservoirs during waterflooding and oil displacement[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(5): 113-121. doi: 10.11885/j.issn.1674-5086.2017.10.09.01 |
| [20] |
陈森, 林伯韬, 金衍, 等. SAGD井微压裂储层渗透率变化规律研究[J]. 西南石油大学学报(自然科学版), 2018, 40(1): 141-148. CHEN Sen, LIN Botao, JIN Yan, et al. Study on patterns of change in oil reserve permeability during microfracturing of SAGD wells[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(1): 141-148. doi: 10.11885/j.issn.1674-5086.2016.06.21.05 |
| [21] |
吴素英. 长期注水冲刷储层参数变化规律及对开发效果的影响[J]. 大庆石油地质与开发, 2006, 25(4): 35-37. WU Suying. Variation rule of oil layer parameters washed by long-term injected water and its impact on develop-ment effect[J]. Petroleum Geology & Oilfield Development in Daqing, 2006, 25(4): 35-37. doi: 10.3969/j.issn.1000-3754.2006.04.013 |
| [22] |
蔡毅, 杨雷, 赵跃华, 等. 长期水洗前后双河油田储层微观特征变化规律[J]. 大庆石油地质与开发, 2004, 23(1): 24-26. CAI Yi, YANG Lei, ZHAO Yuehua, et al. Ariation law of the micro-geological features of the reservoir before and after a long term water flooding in Shuanghe Oilfield[J]. Petroleum Geology & Oilfield Development in Daqing, 2004, 23(1): 24-26. doi: 10.3969/j.issn.1000-3754.2004.01.008 |
| [23] |
杜庆龙. 长期注水开发砂岩油田储层渗透率变化规律及微观机理[J]. 石油学报, 2016, 37(9): 1159-1164. DU Qinglong. Variation law and microscopic mechanism of permeability in sandstone reservoir during long-term water flooding development[J]. Acta Petrolei Sinica, 2016, 37(9): 1159-1164. doi: 10.7623/syxb201609010 |
| [24] |
张伟, 曹仁义, 罗东红, 等. 南海珠江口盆地海相砂岩油藏高倍数水驱驱替特征[J]. 油气地质与采收率, 2018, 25(2): 64-71. ZHANG Wei, CAO Renyi, LUO Donghong, et al. characteristics of high-multiple water drive in marine sandstone reservoirs in the Pearl River Mouth Basin, South China Sea[J]. Petroleum Geology and Recovery Efficiency, 2018, 25(2): 64-71. doi: 10.13673/j.cnki.cn37-1359/te.2018.02.010 |
| [25] |
张吉磊, 罗宪波, 张运来, 等. 提高稠油底水油藏转注井注水效率研究[J]. 岩性油气藏, 2019, 31(4): 141-148. ZHANG Jilei, LUO Xianbo, ZHANG Yunlai, et al. Improving water injection efficiency of transfer injection well in heavy oil bottom water reservoir[J]. Lithologic Reservoirs, 2019, 31(4): 141-148. doi: 10.12108/yxyqc.20190415 |
| [26] |
陆小兵, 张吉磊, 杨小龙, 等. 一种解除低渗透油田注水井井底滤饼堵塞的新方法[J]. 钻采工艺, 2015, 38(3): 56-58. LU Xiaobing, ZHANG Jilei, YANG Xiaolong, et al. A new method for removing blockage of bottom filter cake in water injection well of low permeability oilfield[J]. Drilling & Production Technology, 2015, 38(3): 56-58. doi: 10.3969/J.issn.1006-768X.2015.03.17 |
 2020, Vol. 42
2020, Vol. 42


